- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы обработки числовых данных презентация
Содержание
- 1. Методы обработки числовых данных
- 2. Методы обработки числовых данных Таблицы Экспериментальные данные
- 3. Интерполяция Сущность интерполяции состоит в отыскании значения
- 4. Интерполяция по Лагранжу Интерполяционный полином – многочлены степени n Система уравнений или
- 5. Интерполяция по Лагранжу
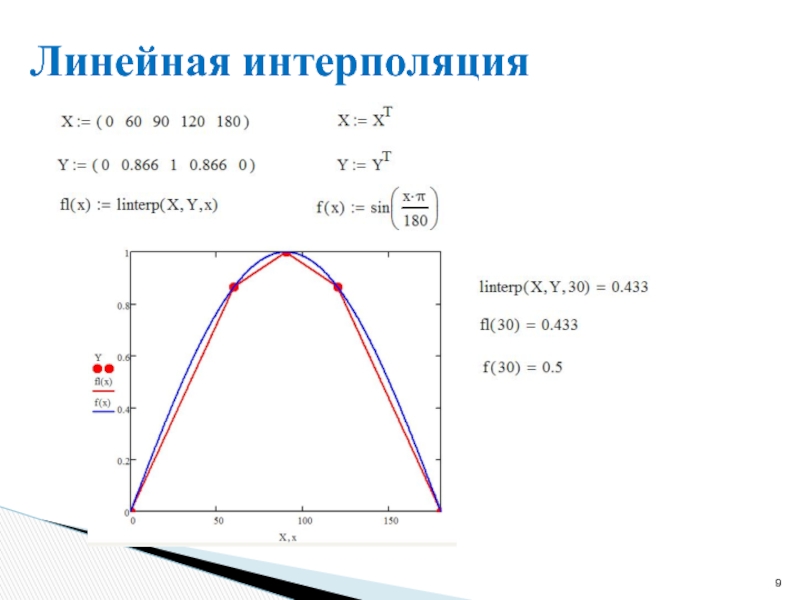
- 6. Линейная интерполяция
- 7. Линейная интерполяция Уравнение прямой, проходящей через 2 точки
- 8. Линейная интерполяция (Mathcad) linterp(X,Y,x) X –
- 9. Линейная интерполяция
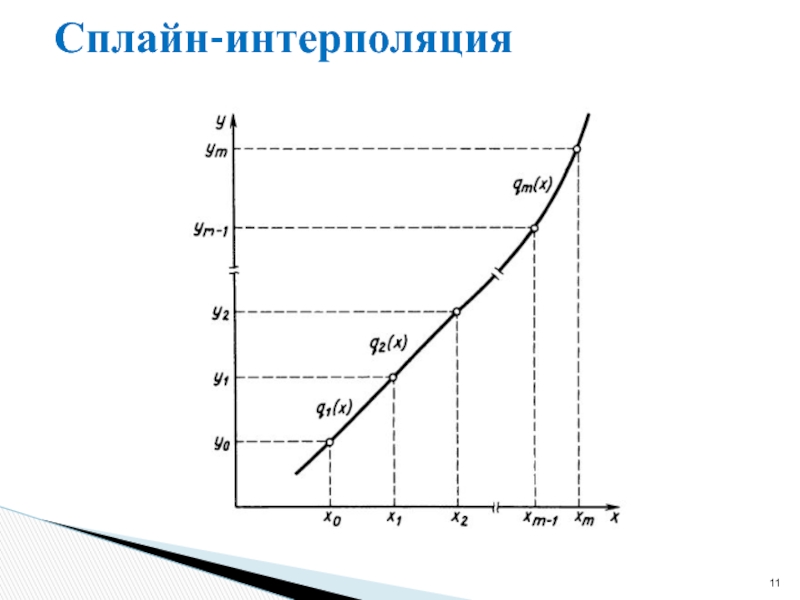
- 10. Сплайн-интерполяция Сплайн – это группа сопряженных
- 11. Сплайн-интерполяция
- 12. Сплайн-интерполяция ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СПЛАЙНОВ Условие непрерывности сплайна
- 13. Сплайн-интерполяция При таком выборе кубических многочленов автоматически
- 14. Сплайн-интерполяция Система уравнений Существуют и другие
- 15. Сплайн-интерполяция (Mathcad) interp(vs,X,Y,x) vs - вектор
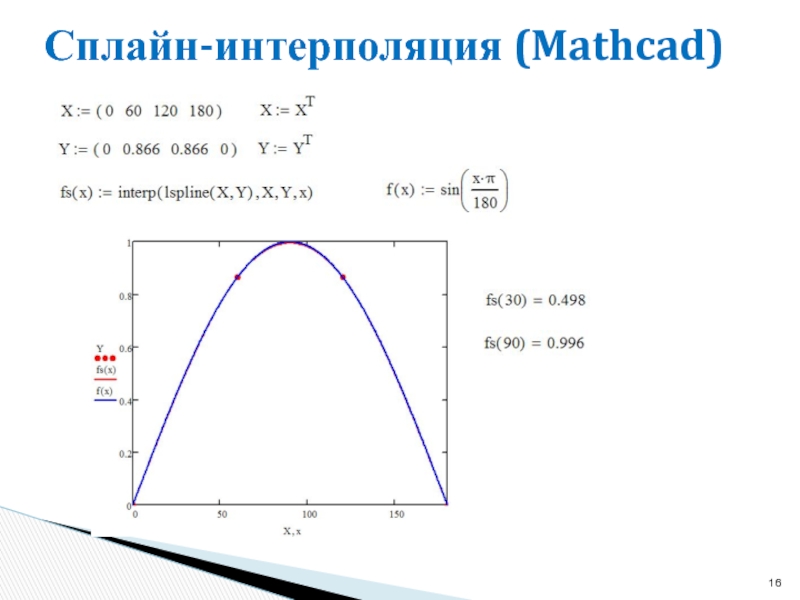
- 16. Сплайн-интерполяция (Mathcad)
- 17. Обработка экспериментальных данных Метод наименьших квадратов
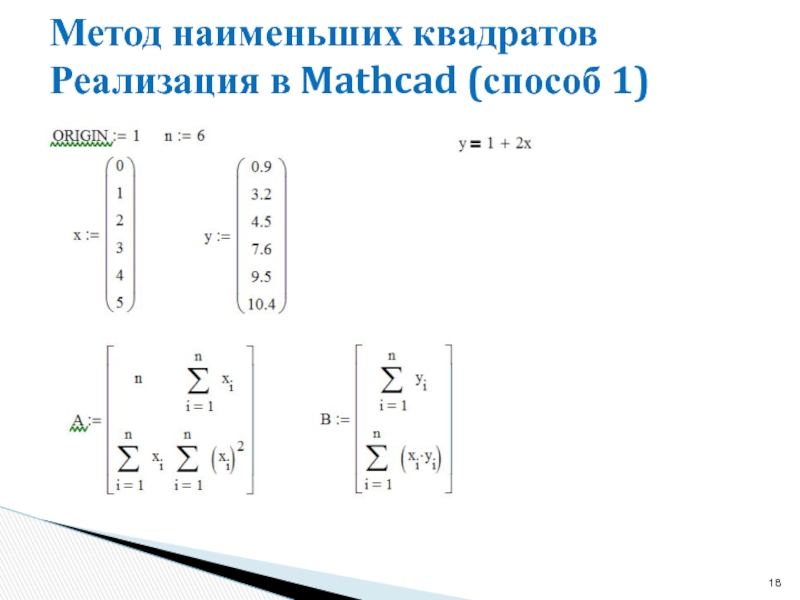
- 18. Метод наименьших квадратов Реализация в Mathcad (способ 1)
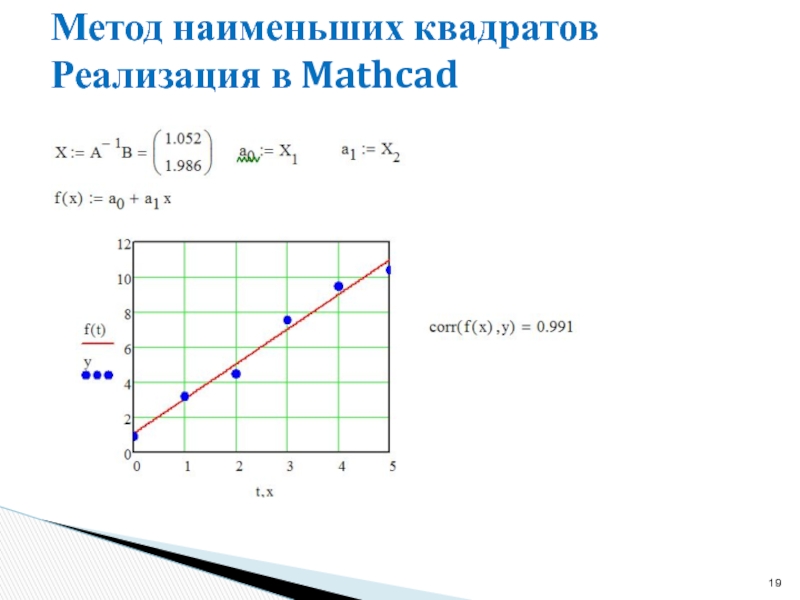
- 19. Метод наименьших квадратов Реализация в Mathcad
- 20. Метод наименьших квадратов Реализация в Mathcad (способ 2)
- 21. Задание Написать функцию с использованием C++Builder, аналогичную
- 22. Контрольные вопросы Использование линейной и сплайн-интерполяции в
- 23. Благодарю за внимание!
Слайд 2Методы обработки
числовых данных
Таблицы
Экспериментальные данные
2 подхода
Интерполяция - аппроксимирующая функция должна пройти через
Регрессия - аппроксимирующая функция не обязательно должна проходить через все точки
Цель
Получение функциональной зависимости y = f(x)
Числовые данные
Слайд 3Интерполяция
Сущность интерполяции состоит в отыскании значения функции в некоторой промежуточной точке
Виды
интерполяция по Лагранжу;
линейная;
квадратичная;
сплайн-интерполяция.
Слайд 8Линейная интерполяция (Mathcad)
linterp(X,Y,x)
X – вектор табличных значений аргумента;
Y – вектор табличных
x – значение аргумента, при котором вычисляется интерполирующее значение функции.
Слайд 10Сплайн-интерполяция
Сплайн – это группа сопряженных кубических многочленов, в местах сопряжения которых
Такие функции называют кубическими сплайнами.
Слайд 12Сплайн-интерполяция
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СПЛАЙНОВ
Условие непрерывности сплайна
Условие непрерывности первых производных
Условие непрерывности
«Естественные» краевые условия
Слайд 13Сплайн-интерполяция
При таком выборе кубических многочленов автоматически удовлетворяются все условия, кроме условий,
Условие непрерывности вторых производных
для внутренних точек
для двух внешних
Слайд 14Сплайн-интерполяция
Система уравнений
Существуют и другие сплайны, получающиеся при других условиях на
Система уравнений – трехдиагональная
Для решения таких систем используется метод прогонки
Слайд 15Сплайн-интерполяция (Mathcad)
interp(vs,X,Y,x)
vs - вектор вторых производных, созданный функцией lspline(X,Y), spline(X,Y) или
X – вектор табличных значений аргумента;
Y – вектор табличных значений функции;
x – значение аргумента, при котором вычисляется интерполирующее значение функции.
lspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к прямой линии в граничных точках;
pspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к квадратичной параболе в граничных точках;
cspline(X,Y) – создает вектор коэффициентов кривой, которая приближается к кубической параболе в граничных точках.
Слайд 21Задание
Написать функцию с использованием C++Builder, аналогичную функции linterp в MathCAD (линейная
Написать функцию с использованием C++Builder, реализующую интерполяцию по Лагранжу с построением графиков.
Написать функцию с использованием C++Builder, аналогичную функции interp в MathCAD (сплайн-интерполяция) с построением графиков.
Написать функцию с использованием C++Builder для обработки экспериментальных данных методом наименьших квадратов с построением графиков.
Слайд 22Контрольные вопросы
Использование линейной и сплайн-интерполяции в MathCAD.
Реализация метода наименьших квадратов в
Интерполяция по Лагранжу.
Линейная интерполяция.
Сплайн-интерполяция.
Метод наименьших квадратов.