- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитические функции распределения, используемые в гидрологии презентация
Содержание
- 1. Аналитические функции распределения, используемые в гидрологии
- 2. Нормальное распределение Функция плотности вероятности График
- 3. Интегральная функция нормального распределения
- 4. Нормирование случайной величины Нормирование СВ осуществляется
- 5. Переход от нормированных значений
- 6. Закон равномерной плотности
- 7. Интегральная функция распределения закона равномерной
- 8. Логарифмически нормальное распределение
- 9. Интегральная и дифференциальная функции
- 10. Характеристики логнормального распределения
- 11. Характеристики логнормального распределения (2) Наибольшее соответствие
- 12. Последовательность расчетов среднегодовых
- 13. Последовательность расчетов (1 вариант)
- 14. Последовательность расчетов (2 вариант)
- 15. Трехпараметрическое логнормальное распределение
- 16. Закон распределения крайних
- 17. Распределение Гумбеля (продолжение)
- 19. Распределение Гумбеля (продолжение) Теңдеуі: және q және
- 21. Распределение Гумбеля (жалғасы)
- 22. НАЗАРЛАРЫҢЫЗҒА РАХМЕТ!
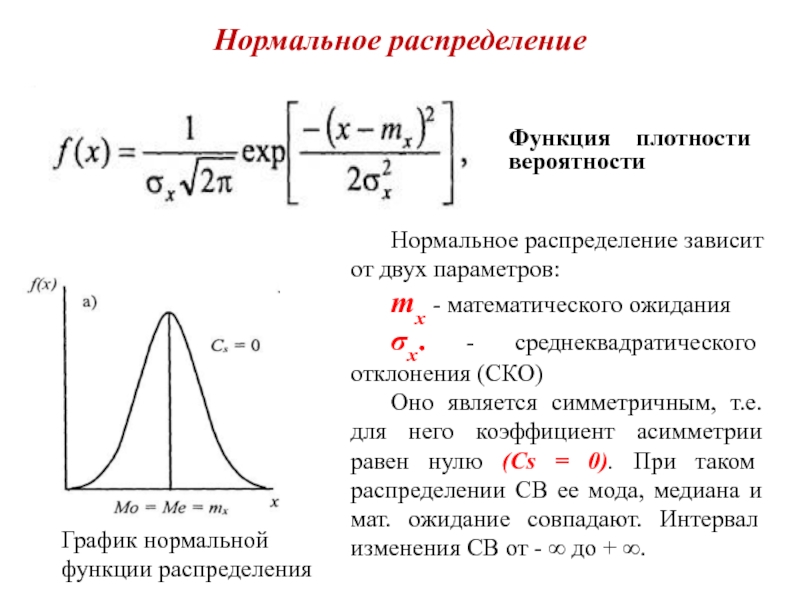
Слайд 2Нормальное распределение
Функция плотности вероятности
График нормальной функции распределения
Нормальное распределение зависит от
mx - математического ожидания
σx. - среднеквадратического отклонения (СКО)
Оно является симметричным, т.е. для него коэффициент асимметрии равен нулю (Cs = 0). При таком распределении СВ ее мода, медиана и мат. ожидание совпадают. Интервал изменения СВ от - ∞ до + ∞.
Слайд 3
Интегральная
функция нормального распределения
Ординаты функции выражаются в виде таблицы.
где z – переменная интегрирования
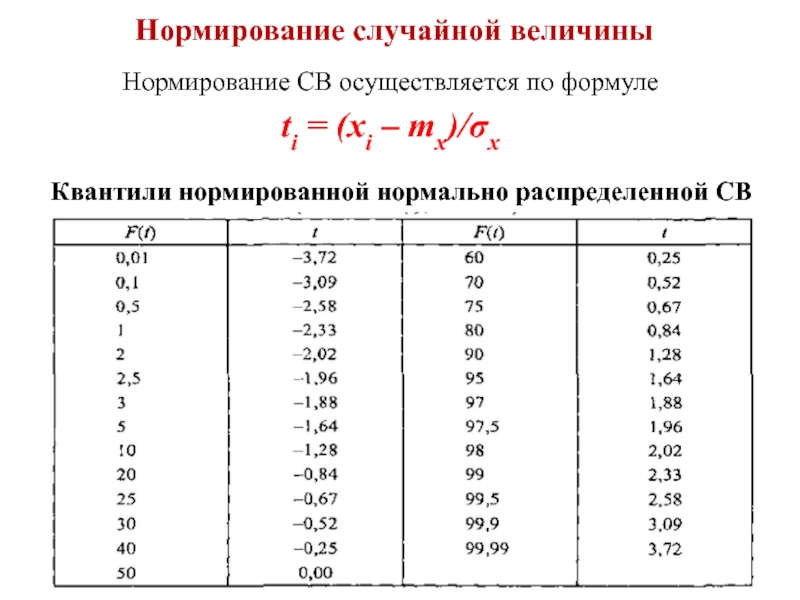
Слайд 4 Нормирование случайной величины
Нормирование СВ осуществляется по формуле
ti = (xi –
Квантили нормированной нормально распределенной СВ
Слайд 5
Переход
от нормированных значений СВ к исходным
Для расчета модульных
Перевод от нормированных значений СВ к исходным осуществляется по формуле xp = tp σx + mx
Нормальный закона
и гидрологические процессы
Расходы воды всегда положительны, а область значений СВ при нормальном распределении изменяется от - ∞ до + ∞
Для нормального распределения Cs = 0, а для многих гидрологических характеристик Cs >0.
Слайд 6
Закон равномерной плотности
СВ Х подчиняется закону равномерной плотности, когда
Дифференциальная функция распределения закона равномерной плотности
Закон равномерной плотности определяется двумя параметрами: началом – а и концом – b интервала изменения СВ Х.
Плотность вероятности равна:
Слайд 7
Интегральная функция
распределения закона равномерной плотности
Характерные особенности закона равномерной плотности
- Медиана равна МО.
- Закон равномерной плотности не имеет Моды
Этот закон используется в гидрологии при моделировании искусственных гидрологических рядов.
Слайд 8
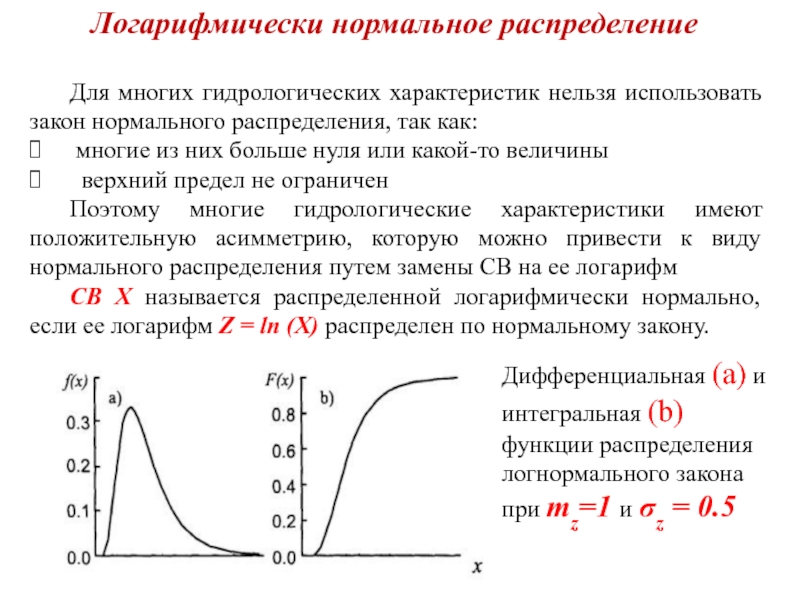
Логарифмически нормальное распределение
Для многих гидрологических характеристик нельзя использовать закон
многие из них больше нуля или какой-то величины
верхний предел не ограничен
Поэтому многие гидрологические характеристики имеют положительную асимметрию, которую можно привести к виду нормального распределения путем замены СВ на ее логарифм
СВ Х называется распределенной логарифмически нормально, если ее логарифм Z = ln (X) распределен по нормальному закону.
Дифференциальная (а) и интегральная (b) функции распределения логнормального закона при mz=1 и σz = 0.5
Слайд 9
Интегральная и дифференциальная
функции логнормального распределении СВ
Интегральная функция логнормального
Дифференциальная функция логнормального распределения
где u = (z- mz)/σz z = ln(x) s – переменная интегрирования
Слайд 10
Характеристики логнормального распределения
Распределение определяется двумя параметрами: mz и
Величина mz – это МО, а σz – это СКО
Дисперсия, СКО и МО связаны соотношениями
Слайд 11 Характеристики логнормального распределения (2)
Наибольшее соответствие эмпирических данных с логнормальным распределением
Мода и медиана для СВ Х, имеющего логнормальное распределение, определяются равенствами:
Ординаты кривой обеспеченности логнормального распределения определяются по таблице стандартного нормального закона распределения, с учетом того, что Z = ln (X)
Cs = 3•Cv + Cv3
где Cv = σ/mx
Коэффициент асимметрии логнормального распределения определяется по формуле
Слайд 12 Последовательность расчетов среднегодовых расходов воды n% обеспеченности – P(n%) при
Так как на практике мы не знаем истинное распределение СВ Х, то допускается два варианта расчета:
оценка mz и σz производится по ряду значений СВ Z
по ряду значений СВ Х производится оценка mx и σx, а затем по формулам
определяется mz и σz
Слайд 13
Последовательность расчетов (1 вариант)
Проводим преобразование исходного ряда наблюдений по
По ряду значений СВ Z приближенно определяем mz и σz (методика расчета будет изложена в последующих лекциях)
Вычисляем вероятность непревышения F(n%)=100 – P(n%)
По таблице квантилей для нормированной нормально распределенной СВt определяем F(n%) квантиль
по формуле xp=tpσp + mx определяем zp(n%) = tp(n%)σz + mz
Так как zp(n%) = ln Qp(n%), то Qp(n%) = exp (zp(n%)
Слайд 14
Последовательность расчетов (2 вариант)
По исходному ряду определяем приближенно
Вычисляем mz и σz по формулам
Дальнейший расчет проводится аналогично первому варианту
Слайд 15
Трехпараметрическое логнормальное распределение
В этом распределении вместо преобразования Z =
Параметр a связан с коэффициентом асимметрии соотношением
где k0 – минимальный модульный коэффициент, k0 = a/mx. При k0 = 0, это выражение превращается в выражение
Этот тип распределения рекомендуется использовать при
Слайд 16
Закон распределения
крайних членов выборки (распределение Гумбеля)
Закон разработан для
Функция обеспеченностей закона Гумбеля выглядит так
где у – безразмерная величина, связанная с х выражением
y = α(x – q)
где q - мода СВ Х, которая определяется в зависимости от среднего значения и СКО исходного ряда по формуле
а величину α можно выразить как
Слайд 17
Распределение Гумбеля (продолжение)
На практике вместо уравнения
используется уравнение, полученное
Значение ур можно получить из выражения
после двух- кратного логарифмирования
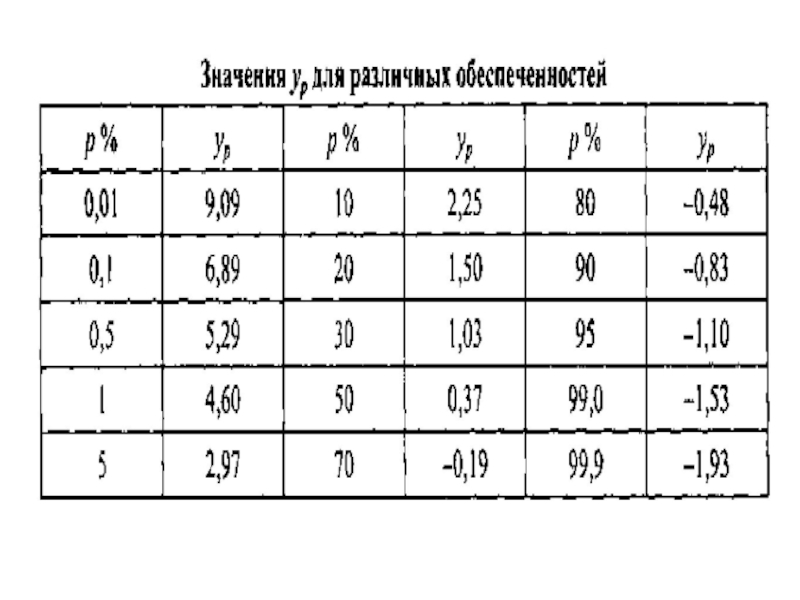
где р - расчетная обеспеченность в процентах. Для основных опорных обеспеченностей значения ур приводятся в таблице
Слайд 19Распределение Гумбеля (продолжение)
Теңдеуі:
және
q және α параметрлерін
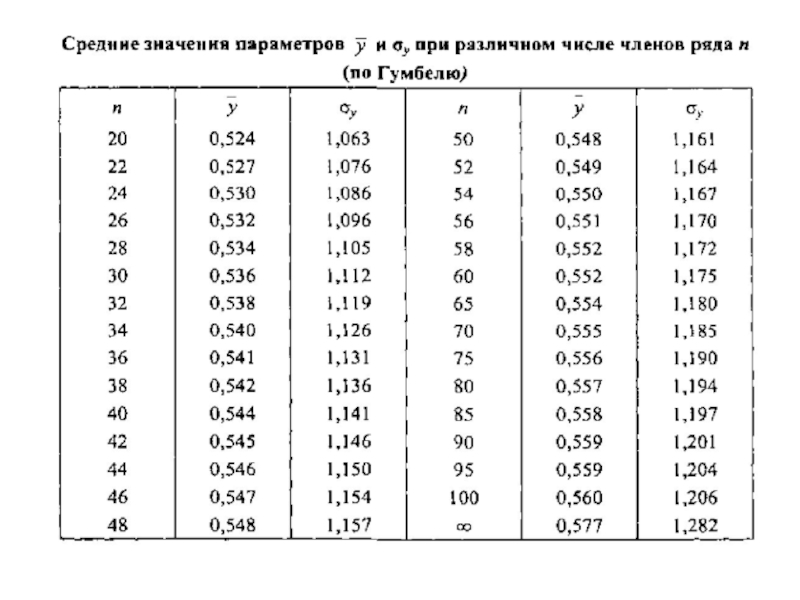
-пен байланыстырады σx при n
Для конечных выборок Гумбель предложил формулы
и
Параметры
и σy определяются в зависимости от длины
анализируемого ряда
Слайд 21
Распределение Гумбеля (жалғасы)
Формуласын ескерсек,
выражение плотности вероятности распределения Гумбеля
Из выражения видно, что для распределения Гумбуля область возможных значений СВ Х находится в интервале (-∞, +∞). Распределение двухпараметрическру т.е. определяется параметрами
и σx.
распределение Гумбеля используется, в основном, при расчете дождевых паводков.