Классическое определение вероятности. Решение задач.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
13-й порок мира взрослых, или Введение в теорию вероятностей (для учащихся 9-х классов ) презентация
Содержание
- 1. 13-й порок мира взрослых, или Введение в теорию вероятностей (для учащихся 9-х классов )
- 2. Москва, Болотная площадь, скульптура Михаила Шемякина “Дети в окружении пороков взрослых”.
- 3. 1. «Алкоголизм»
- 4. 2. «Война»
- 5. 3. «Воровство»
- 6. 4. «Лженауки»
- 7. 5. «Садизм»
- 8. 6. «Нищета»
- 9. 7. «Наркомания»
- 10. 8. «Проституция»
- 11. 9. «Пропаганда насилия»
- 12. 10. «Эксплуатация детского труда»
- 13. 11.Невежество
- 14. 12.Равнодушие.
- 15. 13-й порок. «Приобщения к азартным играм»
- 16. Прежде, чем соглашаться играть, советую подумать
- 17. Игра Кидают 6 шестигранных
- 18. Подумайте, стали бы
- 19. Проверка домашнего задания: №790,792 №790. Выберите 7
- 20. Зарождение теории вероятности произошло в поисках
- 21. Определение вероятности события Если в длинной серии
- 22. Определение вероятности события Вероятностью события называется отношение
- 23. Как найти вероятность события? Для того, чтобы
- 24. Задача №1. Условие Бросаются на стол
- 25. Задача №2 Условие
- 26. Для повторения Расположите в порядке возрастания числа:
- 27. Проверь себя- задача №3 Антон и Игорь
- 28. Ответ/Решение У Игоря шансов выиграть больше,
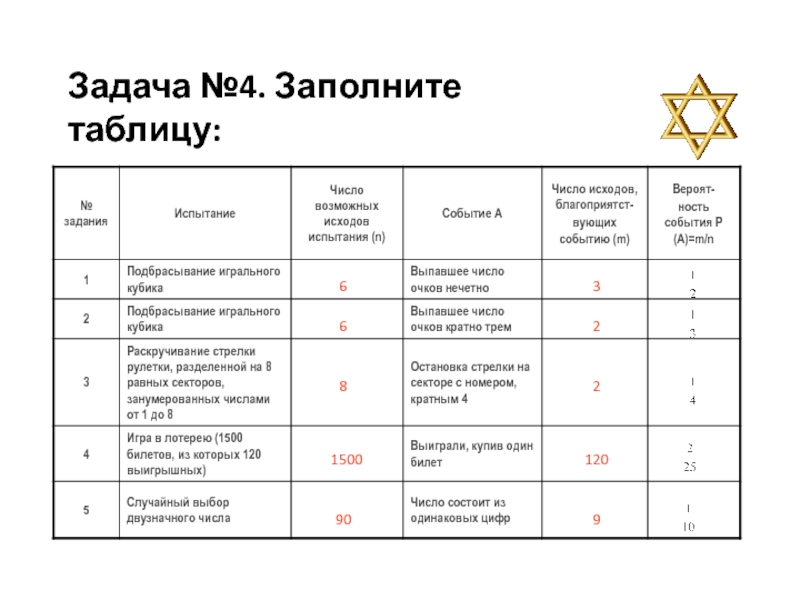
- 29. Задача №4. Заполните таблицу: 6 6 8 1500 90 3 2 2 120 9
- 30. Задача №5. Условие : На четырех
- 31. Задача №6. Условие : На четырех
- 32. Задача №7. Условие: в ящике лежат 1
- 33. Задача №8. Условие: Монету бросают три раза.
- 34. Решить дома. Кидают 6 шестигранных карандашей,
- 35. Домашнее задание. № 803, 804, 805, 806, выучить определения и формулы.
- 36. “Болен игрой” – такой диагноз в
Слайд 1"13-й порок мира взрослых", или Введение в теорию вероятностей (для учащихся
Слайд 1513-й порок. «Приобщения к азартным играм»
Самый распространенный тип зависимости среди молодежи
Очень часто можно наткнуться на лохотронщиков, они преграждают путь, хватают за рукава, ничего не боятся.
И что самое ужасное, некоторые соглашаются сыграть!
Азартные игры появились практически на заре человечества. Сначала это были игральные кости, сводившие с ума еще древних египтян; затем появились карты, рулетка.
Слайд 16
Прежде, чем соглашаться играть, советую подумать и все просчитать- какие условия
Слайд 17Игра
Кидают 6 шестигранных карандашей, на каждой грани –
Слайд 18
Подумайте, стали бы вы играть в эту игру?
Не спешите давать ответ, подсчитайте, что чаще выпадает: очки от 6 до 15 и от 30 до 36, или очки от 15 до 30.
Слайд 19Проверка домашнего задания: №790,792
№790. Выберите 7 строк произвольного текста. Проведя подсчет
№792. Проделайте дома такой опыт: подбросьте 50 раз монету достоинством 1 руб. и подсчитайте, сколько раз выпадет орел. Запишите результаты в тетрадь. В классе подсчитайте, сколько всеми учениками было проведено опытов и каково общее число выпадений орла. Вычислите относительную частоту выпадения орла при бросании монеты.
Слайд 20
Зарождение теории вероятности произошло в поисках ответа на вопрос: как часто
Слайд 21Определение вероятности события
Если в длинной серии одинаковых опытов со случайными исходами
Такой подход к определению вероятности называется статистическим.
Слайд 22Определение вероятности события
Вероятностью события называется отношение m благоприятствующих исходов события
Такой подход к определению вероятности называется классическим.
Слайд 23Как найти вероятность события?
Для того, чтобы найти вероятность события (при классическом
3) найти отношение числа благоприятных для этого события исходов к числу всех исходов испытания.
Слайд 24Задача №1.
Условие
Бросаются на стол 2 игральных кубика. Нам надо, чтобы
Решение
Сколько всего вариантов выпадения очков на 2 кубиках возможно? Подсчитаем с помощью комбинаторного правила умножения: на первом – 6, и для каждого из них – любой из 6 способов на втором. Значит, всего – 36.
Сколько вариантов нам подходит? 5очков=1+4, 2+3, 3+2, 4+1, т.е. 4 варианта.
Подходит – 4 способа, всего – 36 способов. Значит, вероятность того, что выпадет 5 очков: р = 4/36 = 1/9.
Слайд 25 Задача №2
Условие
А теперь ответим на вопрос: какая
2 очка,3очка,4очка, 5очков,6очков, 7очков,8очков, 9очков, 10очков, 11очков, 12очков?
Решение
Всего исходов: 6*6=36
2очка=1+1 (1 способ); р=1/36.
3очка=1+2, 2+1 (2 способа);
р=2/36=1/18.
4очка=1+3, 2+2, 3+1 (3 способа);
р=3/36=1/12.
5очков= 1+2, 2+3, 3+2, 4+1(4 способа);
р=4/36=1/9.
6очков=1+5, 2+4, 3+3, 4+2, 5+1 (5 сп); р=5/36.
7очков= 1+6, 2+5, 3+4, 4+3, 5+2, 6+1 (6 способов); р=6/36=1/6.
8очков=2+6, 3+5, 4+4, 5+3, 6+2
(5 способов); р=5/36.
9очков=3+6, 6+3, 4+5, 5+4 (4 способа); р=4/36=1/9.
10очков=4+6, 5+5, 6+4 (3 способа);
р=3/36=1/12.
11очков=5+6, 6+5 (2 способа);
р=2/36=1/18.
12очков=6+6 (1 способ); р=1/36.
Чаще всего выпадает 7 очков!
Слайд 26Для повторения
Расположите в порядке возрастания числа:
1/36, 1/6, 1/12, 1/18, 1/9.
Ответ: 1/36
Правило: если числители дробей одинаковые, то меньше та дробь, чей знаменатель больше.
Слайд 27Проверь себя- задача №3
Антон и Игорь бросают белый и черный игральные
Слайд 28Ответ/Решение
У Игоря шансов выиграть больше, чем у Антона.
Пусть событие
Пусть событие В означает, что при бросании кубиков в сумме выпало 7 очков.
Для события А благоприятными являются 5 исходов (2,6),(3,5),(4,4),(5,3),(6,2).
Для события В благоприятными являются 6 исходов (1,6),(2,5),(3,4),(4,3),(5,2),(6,1).
Общее число равновозможных исходов: 6*6=36.
Вероятность наступления событий:
Р(А)=5/36, Р(В)=6/36=1/6. (5/36<6/36).
Слайд 30Задача №5.
Условие :
На четырех карточках написаны буквы О, Т, К,
Затем открыли наугад последовательно
эти карточки и положили в ряд.
Какова вероятность того, что получится
слово «КРОТ»?
Решение:
Исходы – все возможные перестановки из четырех элементов (О, Т, К, Р); общее число исходов: n=P₄ =4!=24
Событие А = {после открытия карточек получится слово «КРОТ»}: m=1
p(A)= m/n=1/24.
Т
Р
О
К
Слайд 31Задача №6.
Условие :
На четырех карточках написаны цифры 1, 2, 3, 4.
Решение:
Исходами опыта являются все возможные размещения четырех карточек на трех местах (порядок расположения важен). Общее число исходов:
Событие А- из трех карточек образовано число 123, число благоприятных этому событию исходов m=1.
1
2
3
4
Слайд 32Задача №7.
Условие: в ящике лежат 1 белый и три черных шара.
Решение.
Исходы – все возможные сочетания-пары шаров. Общее число исходов
Событие А={вынуты два черных шара};
Слайд 33Задача №8.
Условие:
Монету бросают три раза. Какое событие более вероятно: событие А-
Решение:
Слайд 34Решить дома.
Кидают 6 шестигранных карандашей, на каждой грани – числа
Слайд 36
“Болен игрой” – такой диагноз в последние годы не является редкостью.
Азартные
Так что, играть или не играть и во что играть – решайте сами!