- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятности презентация
Содержание
- 1. Теория вероятности
- 2. Фенотипический класс – все потомки одного фенотипа
- 3. Почему законы генетики – вероятностные? Передача генов
- 4. Случайное событие Может произойти или не произойти
- 5. Случайное событие нельзя предсказать – если одно
- 6. Вероятность получить двойку на экзамене? Множество возможных событий
- 7. Множество возможных событий Рассмотрим множество событий, включающее
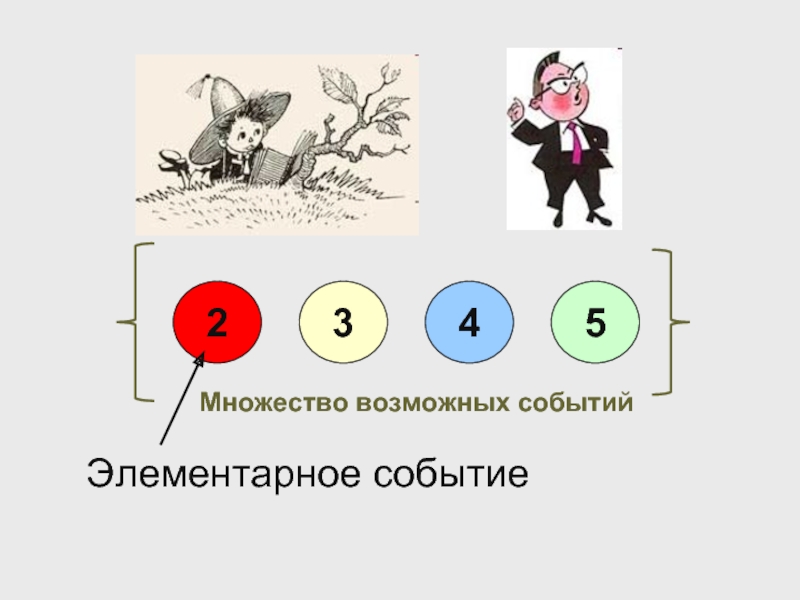
- 8. Множество возможных событий Элементарное событие
- 9. Вероятность Пусть при N испытаниях событие X
- 10. Сумма вероятностей всех элементарных событий (всех возможных
- 11. Иногда проще посчитать вероятность «не X», а
- 12. Множество возможных событий Элементарное событие Вероятность события
- 13. В генетике большую роль играют равновероятные события
- 14. Равновероятные исходы Если эксперимент может закончиться одним
- 15. Равновероятные исходы? Множество возможных событий Какова вероятность того, что сегодня на улице вы встретите динозавра?
- 16. Каждая ячейка – ¼ потомков АА аа
- 17. Вероятность наступления двух независимых событий одновременно:
- 18. Правило умножения Вероятность наступления двух независимых
- 19. Задача Подбрасывание монетки. Вероятность выпадения герба три раза подряд = ?
- 20. Задачи Вероятность, что в семье с тремя
- 21. Задача Какая часть потомков от анализирующего скрещивания
- 22. Вероятность того, что произойдет хотя бы
- 23. Вероятность того, что произойдет хотя бы
- 24. Правило сложения Вероятность того, что произойдет
- 25. Вероятность того, что
- 26. Для несовместных событий правило сложения упрощается
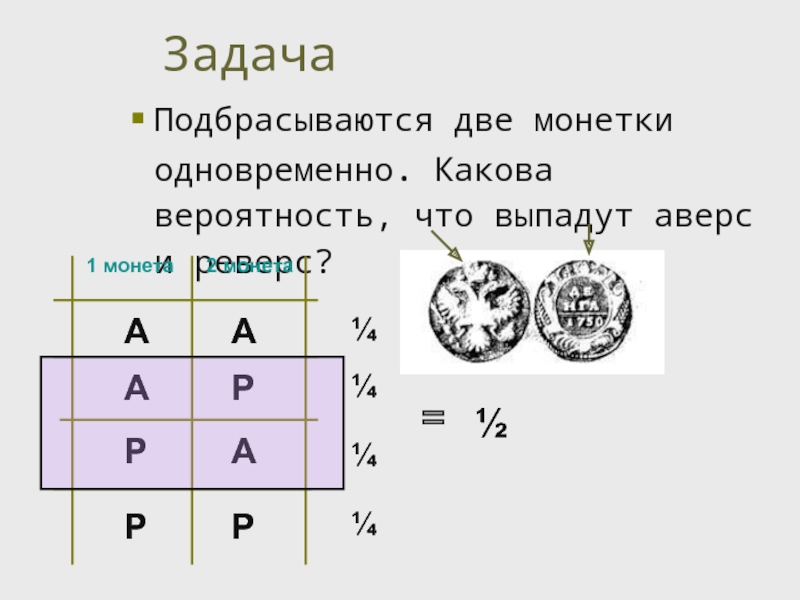
- 27. Задача Подбрасываются две монетки одновременно. Какова вероятность, что выпадут аверс и реверс?
- 28. Какова вероятность того, что среди 4 детей
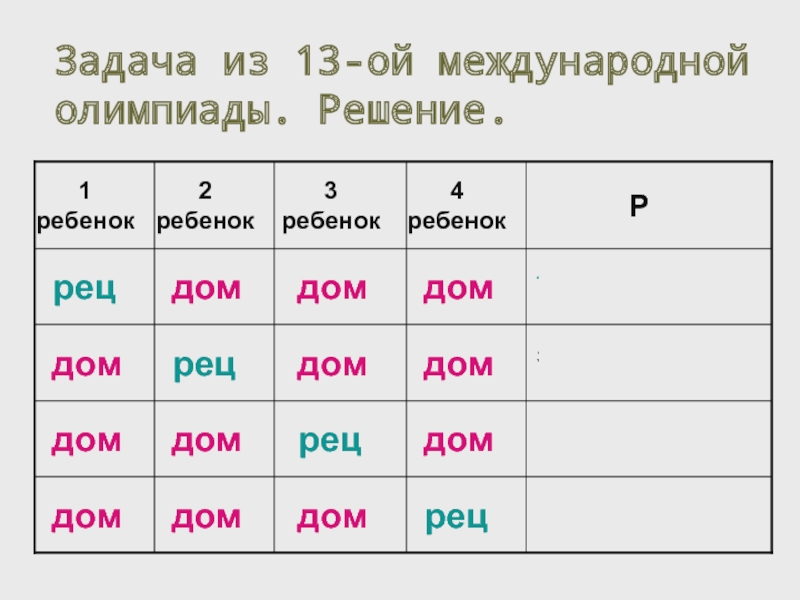
- 29. Задача из 13-ой международной олимпиады. Решение.
- 30. Задача из 13-ой международной олимпиады. Решение. P
- 31. Задача Пусть при выстреле вероятность попадания
- 32. Решение задачи Рассмотрим сначала два выстрела. Пусть
- 33. Решение задачи (продолжение) Аналогично для четырех выстрелов
- 34. Задача У человека есть несколько видов наследственной
- 35. Решение задачи А – доминантный ген слепоты,
- 36. Определение коэффициента родства (процента одинаковых генов) у родственников
- 37. Дано: генотип человека N Найти: вероятность
- 38. отца ⁄ матери братьев ⁄
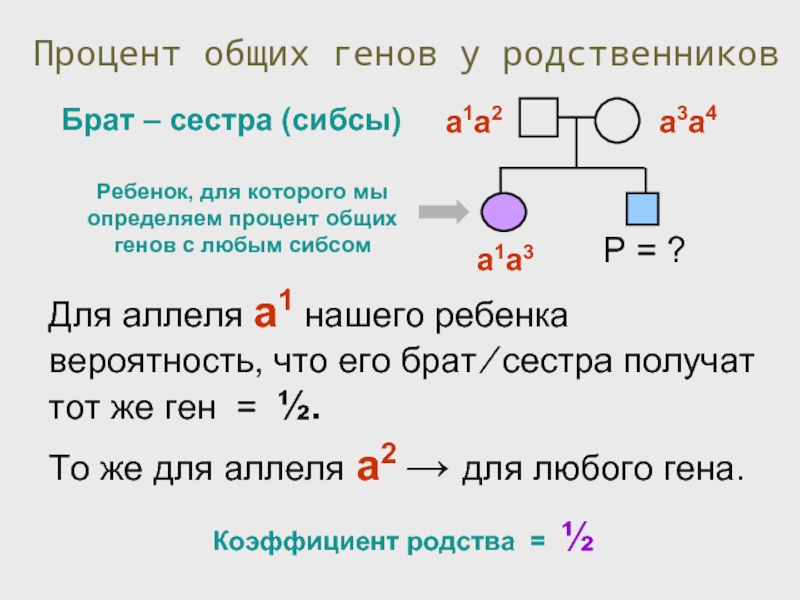
- 39. Процент общих генов у родственников Рассмотрим произвольный
- 40. Для аллеля а1 нашего ребенка вероятность, что
- 41. Процент общих генов у родственников Половину генов
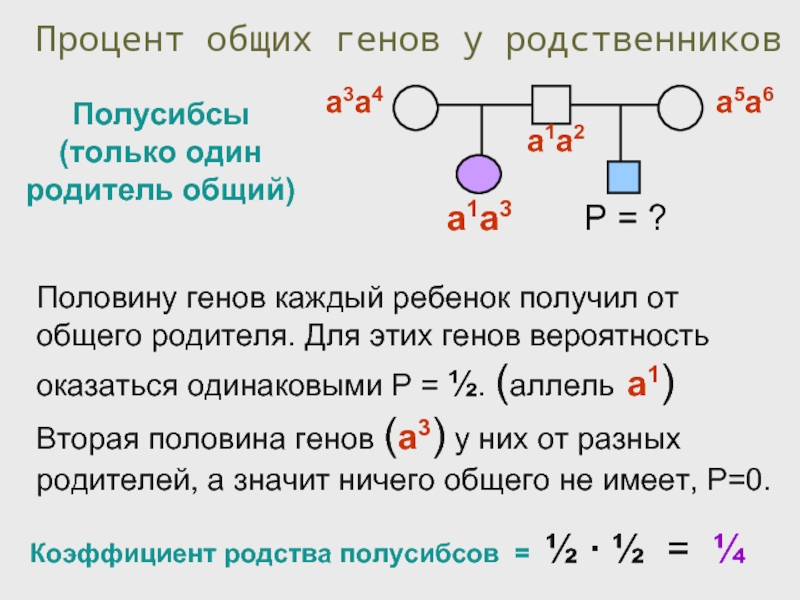
- 42. Другой способ вычисления Полусибсы (только один родитель
- 43. Процент общих генов у родственников Какова вероятность,
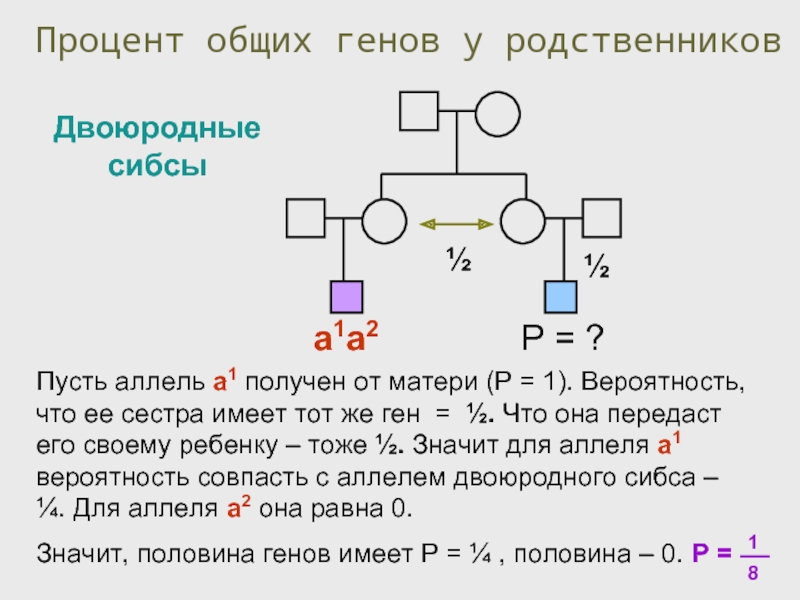
- 44. а1а2 Процент общих генов у родственников Двоюродные сибсы Р = ? ½ ½
- 45. Задача об инбридинге Большинство генов наследственных заболеваний
- 46. Задача об инбридинге. Решение. Аа × АА
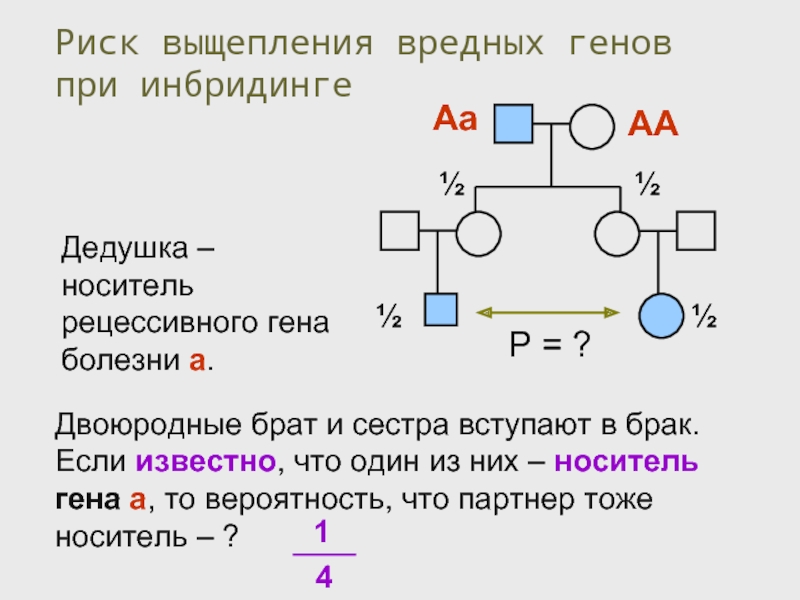
- 47. Двоюродные брат и сестра вступают в брак.
- 48. Двоюродные брат и сестра вступают в брак.
- 49. В следующий раз – о проверке
- 50. Адрес этой презентации http://www.slideshare.net/outdoors Другие
Слайд 2Фенотипический класс – все потомки одного фенотипа
Генотипический класс – все потомки
Расщепление – появление в потомстве разных фенотипических классов.
Выражается в их численном соотношении – 1 : 1, 9 : 3 : 3 : 1 и т.д.
Слайд 3Почему законы генетики – вероятностные?
Передача генов потомкам – это цепь случайных
Расхождение аллелей разных генов по гаметам
Встреча гамет при оплодотворении
Встреча родителей
Слайд 4Случайное событие
Может произойти или не произойти при определенной совокупности условий
Эксперимент, испытание
Нельзя
Слайд 5Случайное событие
нельзя предсказать – если одно
Скрещивание родителей с определенным генотипом.
Каждый потомок – событие.
Генотип одного конкретного потомка предсказать нельзя.
А много – можно!
Слайд 7Множество возможных событий
Рассмотрим множество событий, включающее все возможные исходы испытания.
Элементарное
В генетике – это один из возможных генотипов потомка
Слайд 9Вероятность
Пусть при N испытаниях событие X появилось m раз.
Вероятность Р(Х)
Слайд 10Сумма вероятностей всех элементарных событий (всех возможных исходов эксперимента) всегда равна
Вероятность события «не X» (¬X),
т.е. всех исходов, в которых X не наступило, равна 1 минус вероятность X:
P (¬X) = 1 – P (X)
0 ≤ P ≤ 1
Слайд 11Иногда проще посчитать вероятность «не X», а потом воспользоваться формулой
P (X) = 1 – P (¬X)
Студенты знают ответы на 75% вопросов к зачету. Преподаватель выбирает по два вопроса и задает их студенту.
Вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ – ?
1 – P (не знает ни одного)
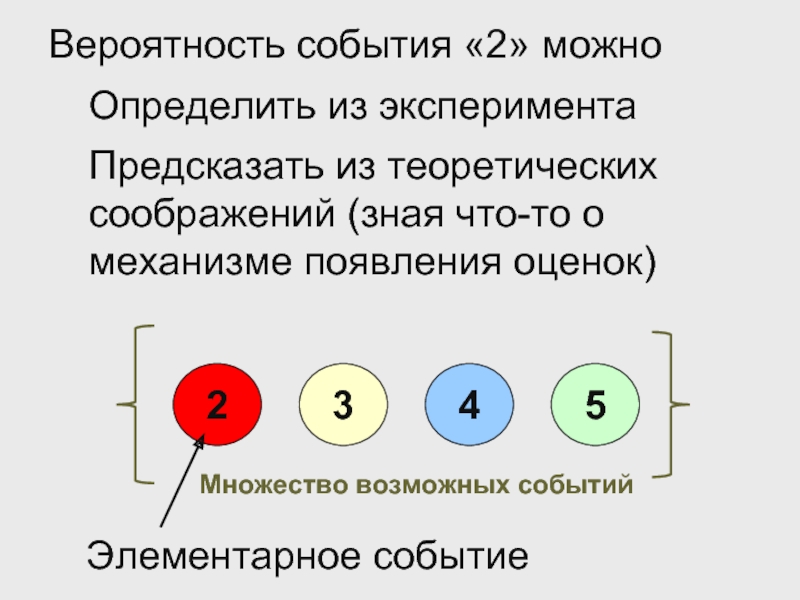
Слайд 12Множество возможных событий
Элементарное событие
Вероятность события «2» можно
Определить из эксперимента
Предсказать из теоретических
Слайд 14Равновероятные исходы
Если эксперимент может закончиться одним из n равновероятных исходов (элементарных
в генетике это – содержимое каждой ячейки в решетке Пеннета
Слайд 15Равновероятные исходы?
Множество возможных событий
Какова вероятность того, что сегодня на улице вы
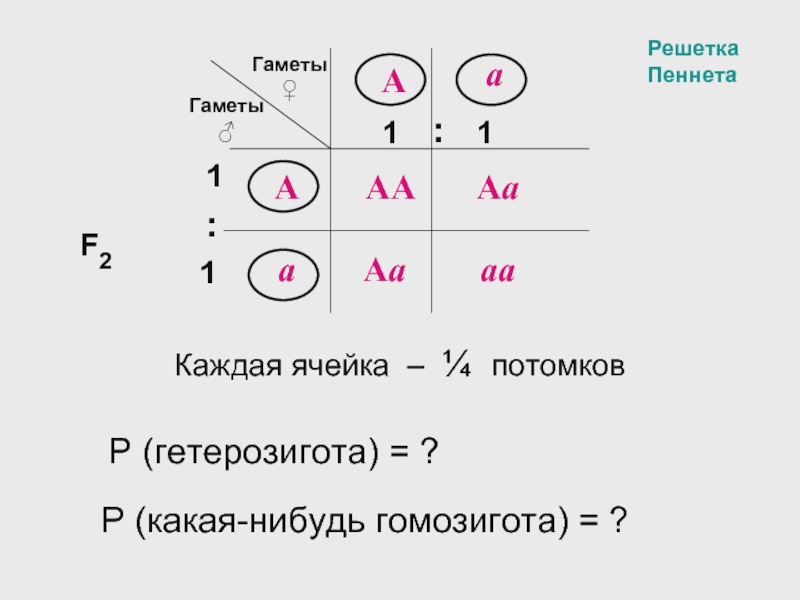
Слайд 16Каждая ячейка – ¼ потомков
АА
аа
Аа
Аа
Решетка Пеннета
Р (гетерозигота) = ?
Р (какая-нибудь гомозигота)
Слайд 17
Вероятность наступления двух независимых событий одновременно: X и Y
Независимыми называются
генотип по гену А и по гену В – независимые события (закон Менделя), если гены А и В – в разных хромосомах
(пересечение множеств X и Y)
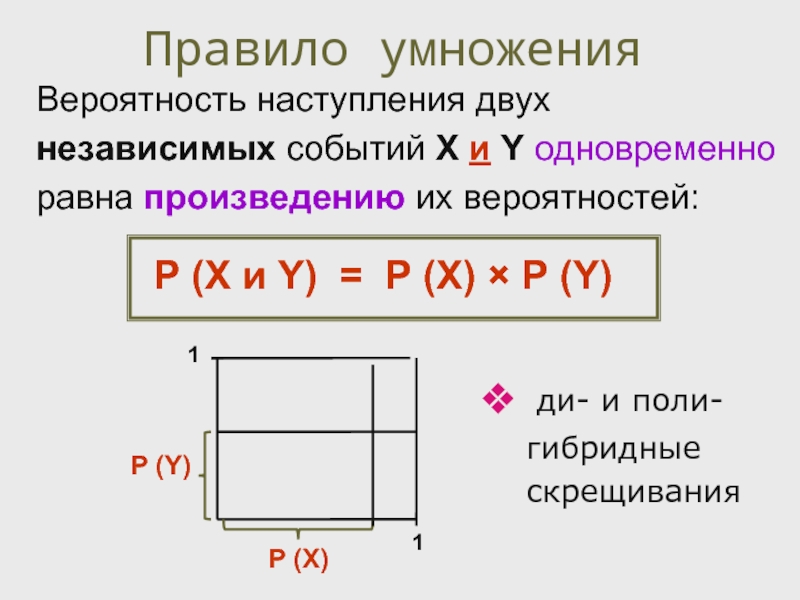
Слайд 18
Правило умножения
Вероятность наступления двух независимых событий X и Y одновременно равна
P (X и Y) = P (X) × P (Y)
ди- и поли-гибридные скрещивания
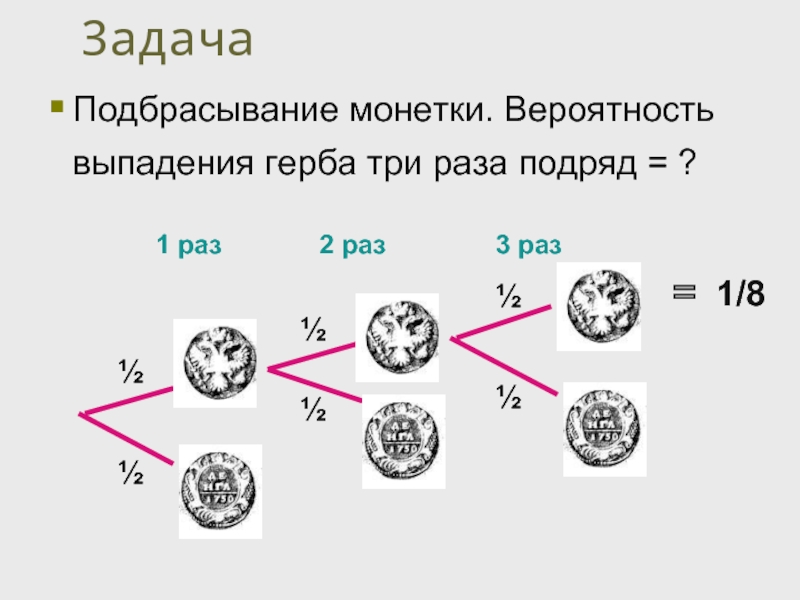
Слайд 20Задачи
Вероятность, что в семье с тремя детьми все трое будут мальчики
В семье уже есть два мальчика.
Какова вероятность, что третий ребенок будет того же пола ?
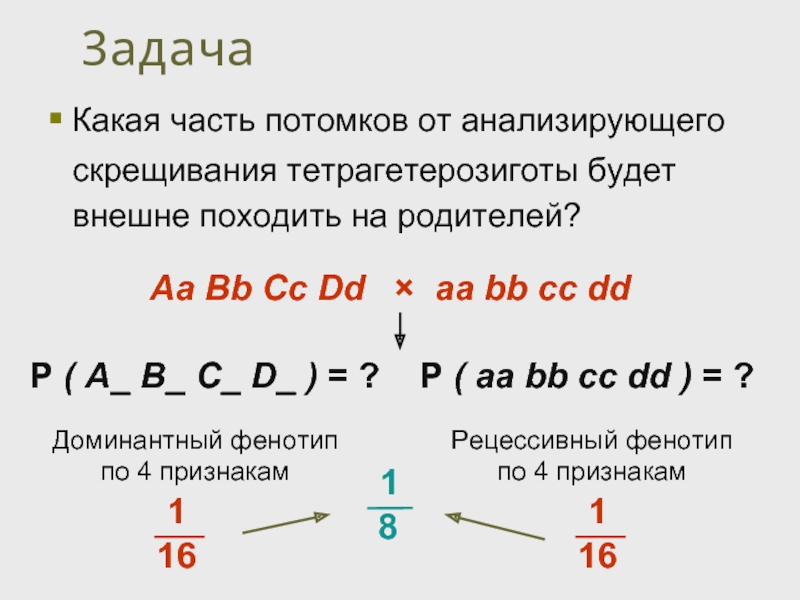
Слайд 21Задача
Какая часть потомков от анализирующего скрещивания тетрагетерозиготы будет внешне походить на
Аa Вb Cc Dd × аа bb cc dd
Р ( А_ В_ C_ D_ ) = ? Р ( аа bb cc dd ) = ?
Доминантный фенотип по 4 признакам
Рецессивный фенотип по 4 признакам
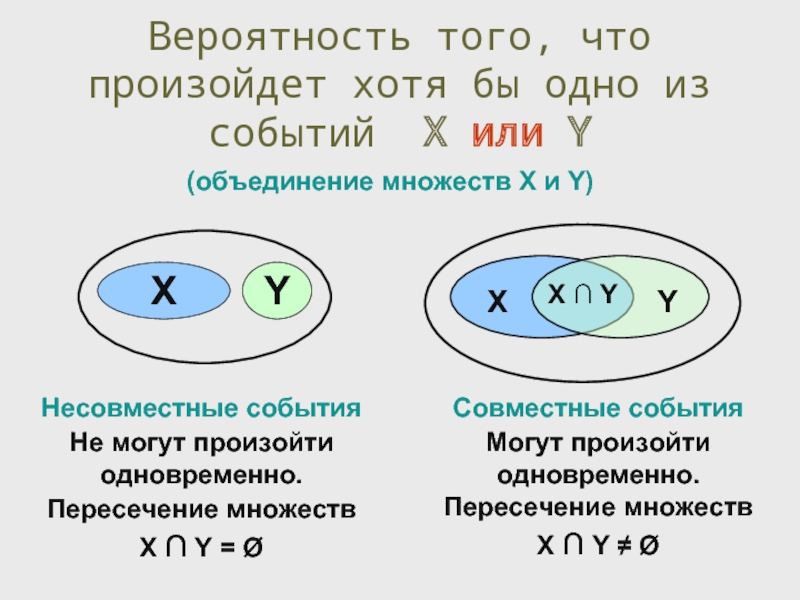
Слайд 22
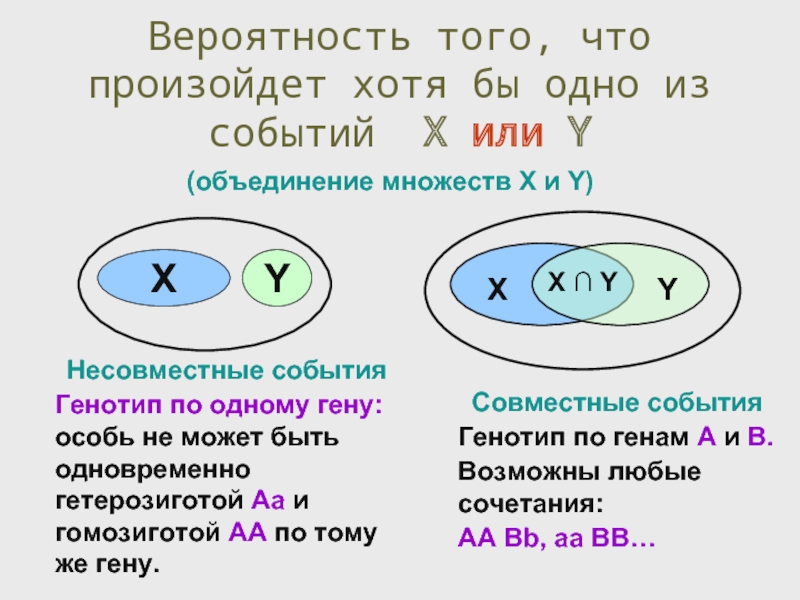
Вероятность того, что произойдет хотя бы одно из событий X или
X
Y
X
Y
X ∩ Y
(объединение множеств X и Y)
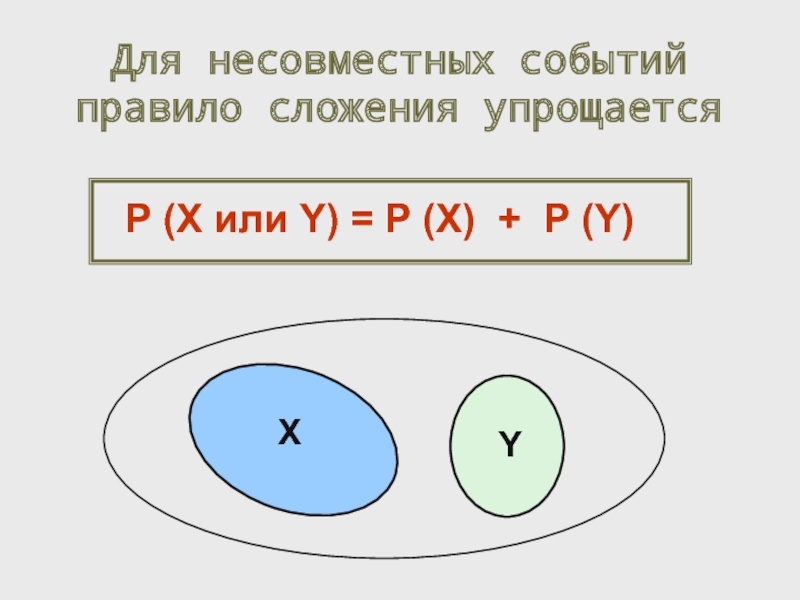
Несовместные события
Не могут произойти одновременно.
Пересечение множеств
X ∩ Y = Ø
Совместные события
Могут произойти одновременно. Пересечение множеств
X ∩ Y ≠ Ø
Слайд 23
Вероятность того, что произойдет хотя бы одно из событий X или
X
Y
X
Y
X ∩ Y
(объединение множеств X и Y)
Несовместные события
Генотип по одному гену: особь не может быть одновременно гетерозиготой Аа и гомозиготой АА по тому же гену.
Совместные события
Генотип по генам А и В.
Возможны любые сочетания:
АА Bb, aa BB…
Слайд 24
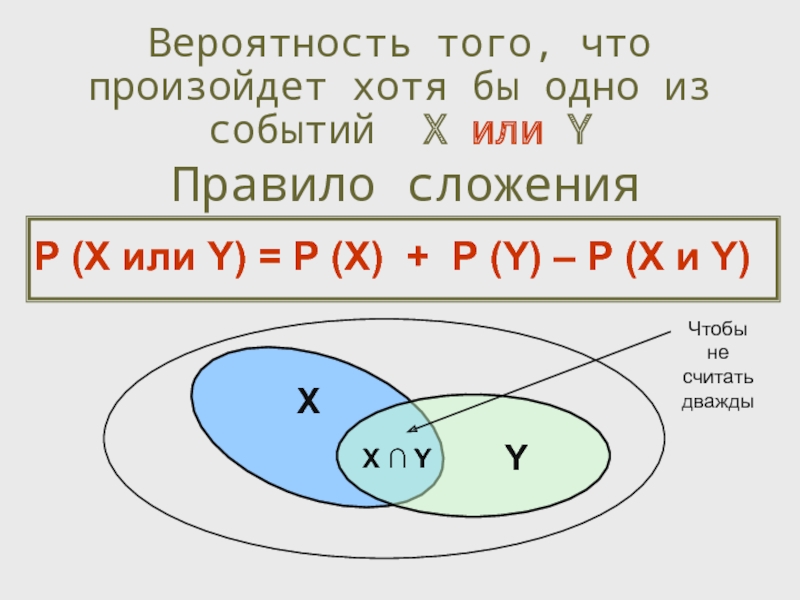
Правило сложения
Вероятность того, что произойдет хотя бы одно из событий X
P (X или Y) = P (X) + P (Y) – P (X и Y)
X
Y
X ∩ Y
Чтобы не считать дважды
Слайд 25
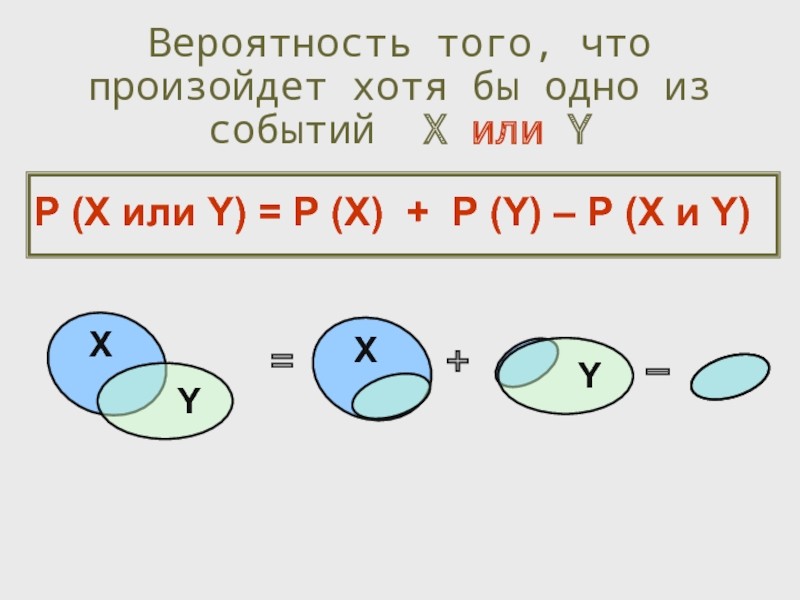
Вероятность того, что произойдет хотя бы одно из событий X или
P (X или Y) = P (X) + P (Y) – P (X и Y)
X
Y
X
Y
=
+
–
Слайд 27Задача
Подбрасываются две монетки одновременно. Какова вероятность, что выпадут аверс и реверс?
Слайд 28Какова вероятность того, что среди 4 детей гетерозиготных родителей (Aa x
Задача из 13-ой международной олимпиады
среди 4 детей один будет иметь рецессивный фенотип
Равнозначна задаче:
Слайд 30Задача из 13-ой международной олимпиады. Решение.
P = 27 ⁄ 44 ∙
= 27 ⁄ 64 = 42 %
Слайд 31Задача
Пусть при выстреле вероятность попадания в мишень – ½.
Какова
Слайд 32Решение задачи
Рассмотрим сначала два выстрела.
Пусть X – попадание в первом, Y
P (X или Y) = P (X) + P (Y) – P (X и Y)
События совместные!
Событие «Не X или Y» – ни одного попадания из двух выстрелов.
Можно проще: 1 – «НЕ X или Y»
Слайд 33Решение задачи (продолжение)
Аналогично для четырех выстрелов проще посчитать вероятность события НИ
Для правила умножения не имеет значения, совместные события или нет! – поэтому так считать проще.
Р (ХОТЯ БЫ ОДНО ПОПАДАНИЕ) = 1 – Р (НИ ОДНОГО ПОПАДАНИЯ)
Слайд 34Задача
У человека есть несколько видов наследственной слепоты, вызываемой разными (неаллельными) генами.
А – доминантный ген слепоты,
b – рецессивный.
Определите вероятность рождения здорового ребенка в семье слепых родителей: отец Аа Вb, мать aa bb
Слайд 35Решение задачи
А – доминантный ген слепоты,
b – рецессивный.
Аа Вb × aa
Генотип здорового ребенка аа В_
и
¼
События совместные!
½ + ½ – ½ ∙½ = ¾
Слайд 37Дано: генотип человека N
Найти: вероятность того, что любой, произвольно выбранный
Имеются ввиду конкретные аллели генов
Слайд 38 отца ⁄ матери
братьев ⁄ сестер (сибсов)
полусибсов (только один
бабушки ⁄ дедушки
двоюродных сибсов
Вероятность найти тот же ген у
Слайд 39Процент общих генов у родственников
Рассмотрим произвольный ген а родителя. В нем
Для а1 она равна ½ . Для а2 –тоже. Значит, для любого аллеля любого гена вероятность совпасть с геном ребенка равна ½
Родитель - ребенок
Коэффициент родства (доля общих генов)
Слайд 40Для аллеля а1 нашего ребенка вероятность, что его брат ⁄ сестра
То же для аллеля а2 → для любого гена.
Процент общих генов у родственников
Брат – сестра (сибсы)
Коэффициент родства = ½
Слайд 41Процент общих генов у родственников
Половину генов каждый ребенок получил от общего
Вторая половина генов (а3) у них от разных родителей, а значит ничего общего не имеет, Р=0.
Полусибсы (только один родитель общий)
Коэффициент родства полусибсов = ½ ∙ ½ = ¼
а1а2
а3а4
а1а3
Р = ?
а5а6
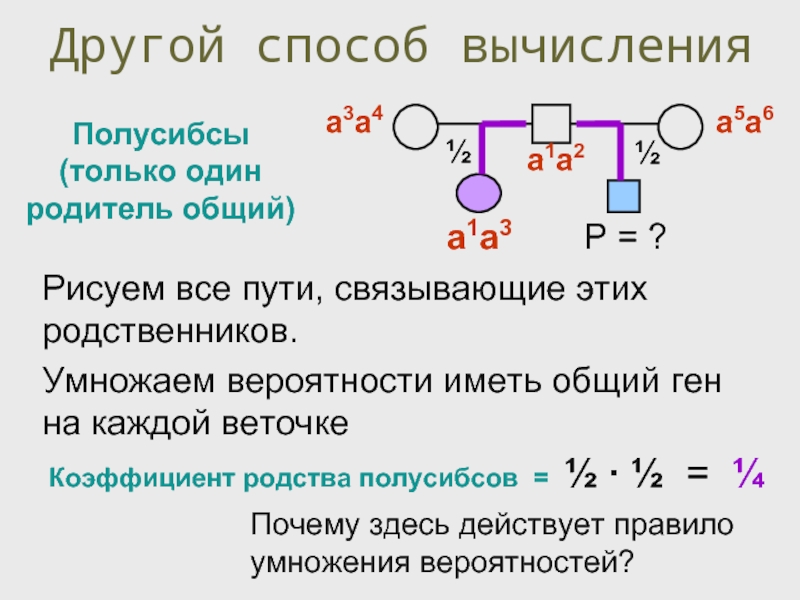
Слайд 42Другой способ вычисления
Полусибсы (только один родитель общий)
Коэффициент родства полусибсов = ½
а1а2
а3а4
а1а3
Р = ?
а5а6
½
½
Рисуем все пути, связывающие этих родственников.
Умножаем вероятности иметь общий ген на каждой веточке
Почему здесь действует правило умножения вероятностей?
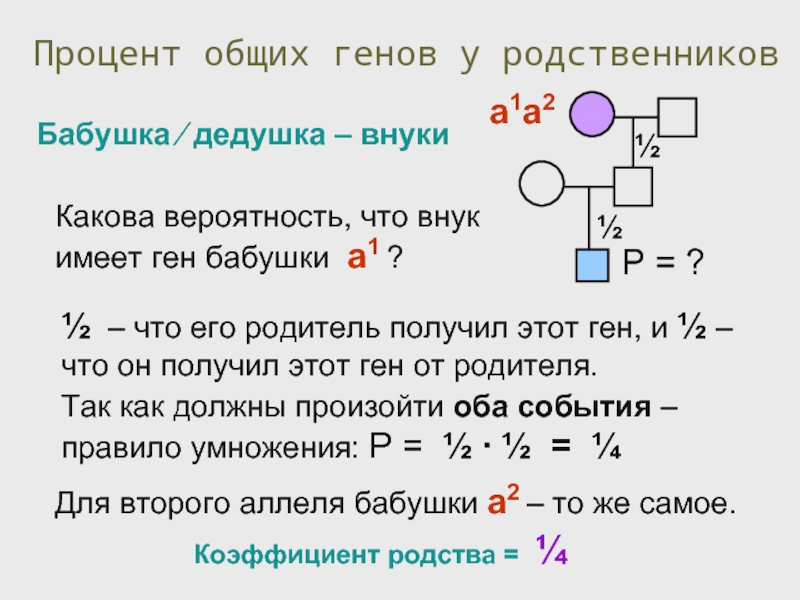
Слайд 43Процент общих генов у родственников
Какова вероятность, что внук имеет ген бабушки
Бабушка ⁄ дедушка – внуки
Для второго аллеля бабушки а2 – то же самое.
½ – что его родитель получил этот ген, и ½ – что он получил этот ген от родителя.
Так как должны произойти оба события – правило умножения: Р = ½ ∙ ½ = ¼
Коэффициент родства = ¼
а1а2
Р = ?
½
½
Слайд 45Задача об инбридинге
Большинство генов наследственных заболеваний человека - рецессивные.
Пусть один из
Пусть ген заболевания получил
Один из детей. Вероятность, что его брат/сестра будут иметь этот же ген - ?
Один из внуков. Вероятность, что его двоюродный сибс будет иметь тот же ген - ? (ген редкий и все остальные родственники здоровы)
Слайд 46Задача об инбридинге. Решение.
Аа × АА
Р
Для двух сибсов (братья-сестры) вероятность иметь
Р (Аа) = ½
Для каждого ребенка
Если известно, что один из них имеет этот ген, то вероятность, что второй имеет тот же ген – ½
Степень родства братьев-сестер (процент общих генов)
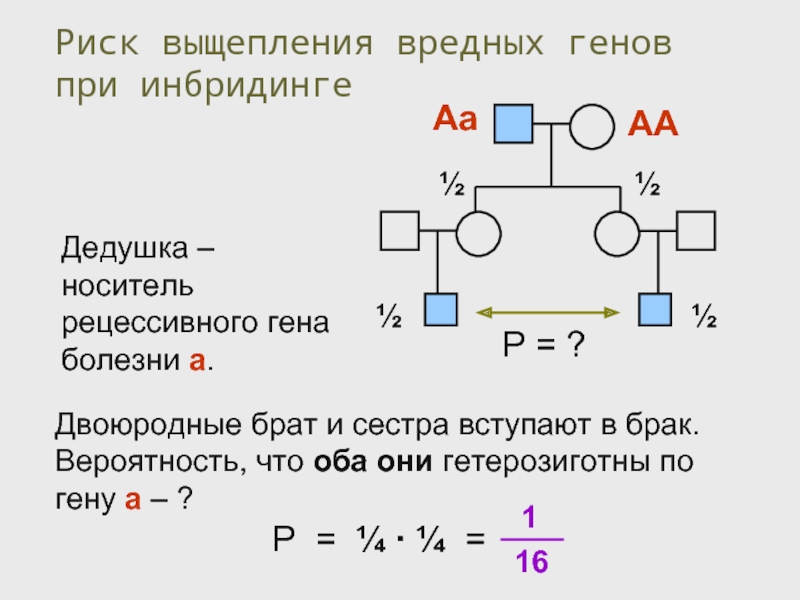
Слайд 47Двоюродные брат и сестра вступают в брак. Вероятность, что оба они
Риск выщепления вредных генов при инбридинге
Дедушка – носитель рецессивного гена болезни а.
Р = ?
½
½
½
½
Слайд 48Двоюродные брат и сестра вступают в брак. Если известно, что один
Риск выщепления вредных генов при инбридинге
Дедушка – носитель рецессивного гена болезни а.
Р = ?
½
Аа
АА
½
½
½
Слайд 49В следующий раз –
о проверке теорий в генетике
Как определить, подтверждает
Слайд 50Адрес этой презентации
http://www.slideshare.net/outdoors
Другие мои лекции по биологии и концепциям современного
http://vatson.hoter.ru/
© Марина Волошина