- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двойной электрический слой. Теория Гельмгольца презентация
Содержание
- 1. Двойной электрический слой. Теория Гельмгольца
- 2. Строение двойного электрического слоя 1. Теория
- 3. Для плоского конденсатора соотношение между разностью потенциалов
- 4. В отличие от физического конденсатора емкость ДЭС
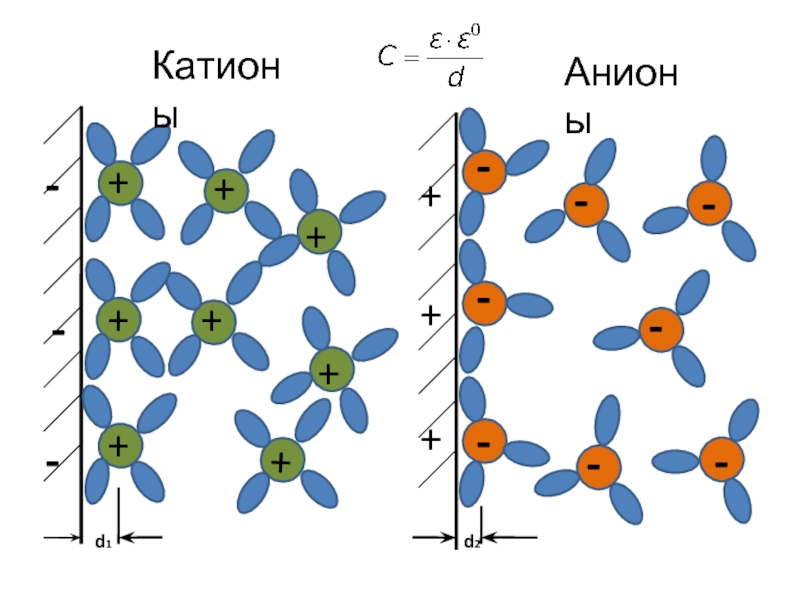
- 5. - - - + + + Катионы Анионы
- 6. Модель строения ДЭС по Гельмгольцу имеет место
- 7. q+ = q- q+ =
- 8. Изменение концентрации ионов по мере удаления от
- 9. где ε – относительная диэлектрическая проницаемость р-ра;
- 10. Теория Гуи – Чапмена не объясняет изменение
- 11. q = q1 + q2
- 13. + Тогда При
- 14. С уменьшением концентрации уменьшение q1 происходит
- 15. Существование плотной части ДЭС может быть обусловлено
- 16. Электрокапиллярные кривые. Уравнения
- 17. Капиллярный электрометр состоит из измерительной бюретки 1,
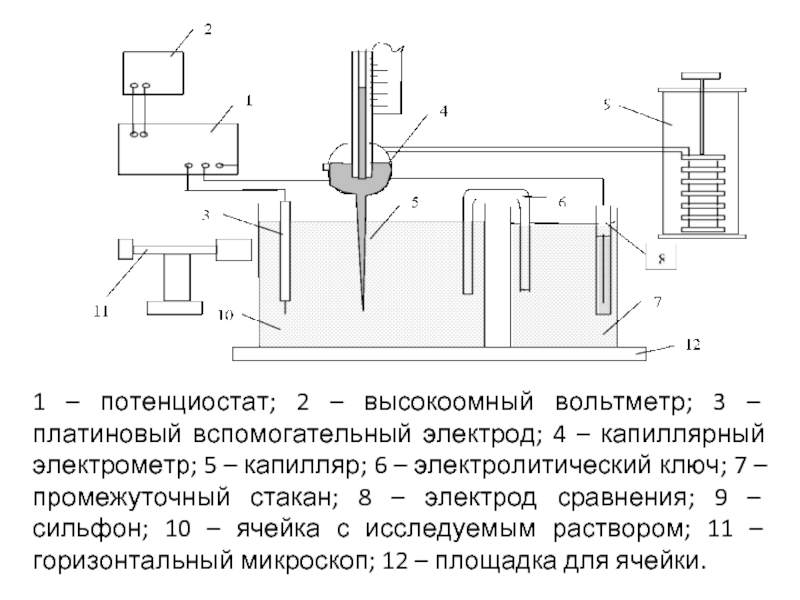
- 18. 1 – потенциостат;
Слайд 2Строение двойного электрического слоя
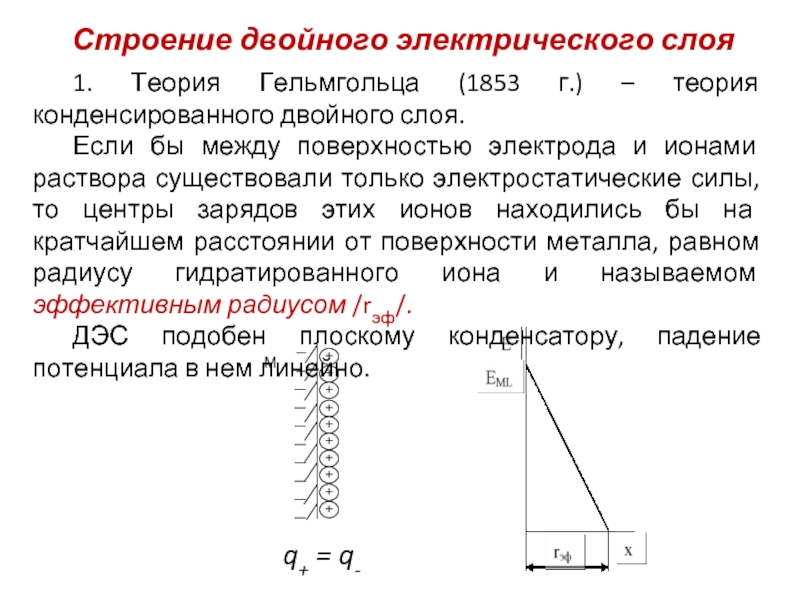
1. Теория Гельмгольца (1853 г.) – теория конденсированного
Если бы между поверхностью электрода и ионами раствора существовали только электростатические силы, то центры зарядов этих ионов находились бы на кратчайшем расстоянии от поверхности металла, равном радиусу гидратированного иона и называемом эффективным радиусом /rэф/.
ДЭС подобен плоскому конденсатору, падение потенциала в нем линейно.
q+ = q-
Слайд 3Для плоского конденсатора соотношение между разностью потенциалов на обкладках и зарядом
q = E . C
где С – емкость конденсатора;
q – заряд.
Емкость конденсатора равна
где ε – относительная диэлектрическая проницаемость раствора, между обкладками конденсатора;
ε0 – абсолютная диэлектрическая проницаемость;
d – расстояние между обкладками.
По аналогии с физическим конденсатором применительно к ДЭС величина С называется емкостью ДЭС, а расстояние между обкладками равно эффективному радиусу иона (d = rэф).
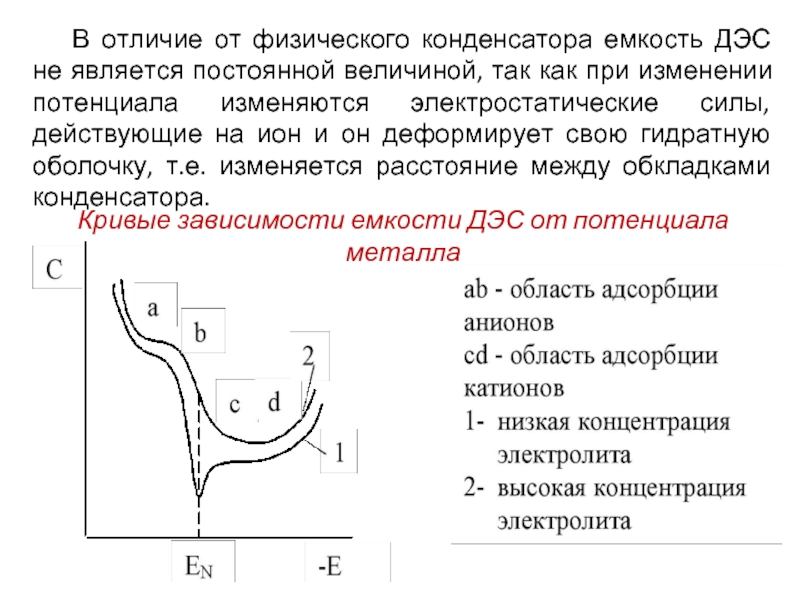
Слайд 4В отличие от физического конденсатора емкость ДЭС не является постоянной величиной,
Кривые зависимости емкости ДЭС от потенциала металла
Слайд 6Модель строения ДЭС по Гельмгольцу имеет место в растворах с ионной
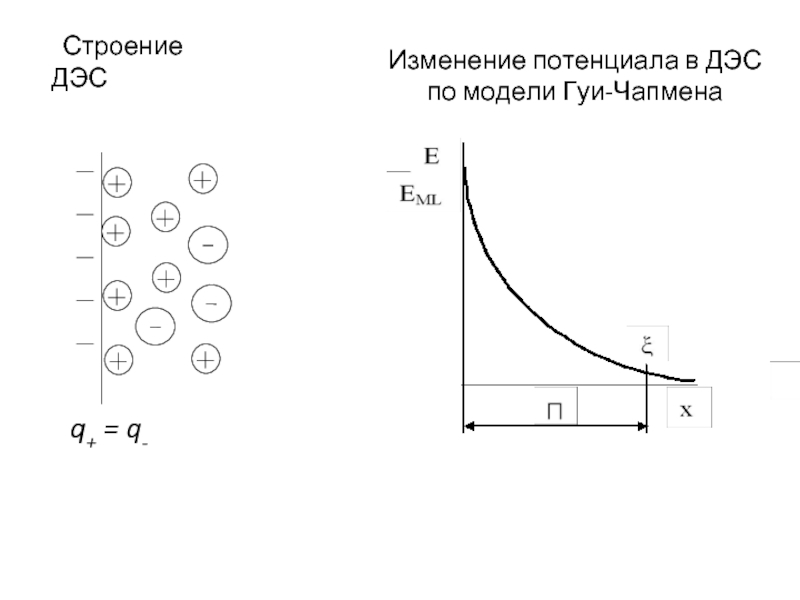
Весьма часто двойной слой имеет более сложное строение. Тепловое движение стремится распределить ионы равномерно в объеме раствора. В результате ионы, компенсирующие заряд поверхности, сосредотачиваются в некотором объеме электролита и концентрация их по мере удаления от поверхности уменьшается.
2. Теория диффузного строения двойного слоя разработана Гуи (1910) и Чапменом (1913 г.)
Слайд 8Изменение концентрации ионов по мере удаления от поверхности электрода можно изобразить
Авторы рассчитали для 1-1 валентного электролита величину удельного поверхностного заряда диффузной жидкостной обкладки ДЭС, считая степень диффузности достаточной для того, чтобы пренебречь собственными размерами ионов:
Слайд 9где ε – относительная диэлектрическая проницаемость р-ра;
ε
R – универсальная газовая постоянная;
T – температура, К;
c – объемная концентрация электролита;
E – потенциал электрода.
На некотором расстоянии ионы не связаны с поверхностью электрода при относительном движении твердой и жидкой фаз. Потенциал на таком расстоянии является электрокинетическим или ξ- потенциалом.
С увеличением концентрации раствора уменьшается степень диффузности и величина ξ- потенциала, что согласуется с опытными данными.
Слайд 10Теория Гуи – Чапмена не объясняет изменение знака ξ- потенциала, т.е.
Эти недостатки вызвали необходимость создания новой теории ДЭС, учитывающей как собственные размеры ионов, так и возможность их специфической адсорбции.
3. Теория Штерна (1924 г. ) – адсорбционная теория двойного слоя.
Штерн полагал, что определенная часть ионов удерживается вблизи поверхности раздела металл – раствор, образуя гельмгольцевскую обкладку двойного слоя с толщиной d = rэф. Остальные ионы образуют диффузный слой с падением потенциала Ψ΄. ξ - потенциал является частью Ψ' – потенциала.
Слайд 11
q = q1 + q2
q1 –
q2 – заряд диффузной части.
Строение ДЭС
Изменение потенциала в ДЭС по модели Штерна
Слайд 12
Ф+, Ф- – энергии адсорбции катионов
Г – поверхностная концентрация ионов в ДЭС;
Ψ΄ – потенциал диффузной части ДЭС;
с – концентрация в объеме электролита.
Заряд диффузной части может быть описан уравнением Гуи:
При наличии специфической адсорбции:
Слайд 13
+
Тогда
При небольших концентрациях единицей в знаменателях первого слагаемого можно пренебречь, тогда
Это
Концентрация электролита входит в выражение для q1 в первой степени, а для q2 – в степени ½. Поэтому при увеличении концентрации электролита увеличение q1 происходит быстрее, чем q2, т.е. q → q1 и диффузность ДЭС уменьшается.
Слайд 14
С уменьшением концентрации уменьшение q1 происходит быстрее, чем q2, т.е. q
Модель строения ДЭС по Штерну объяснила перезарядку поверхности и изменение знака ξ- потенциала.
Строение ДЭС и изменение потенциала в нем
при перезарядке поверхности
Слайд 15Существование плотной части ДЭС может быть обусловлено как электростатическими силами, так
Дальнейшее развитие теории строения ДЭС дано в работах Грэма.
Слайд 16
Электрокапиллярные кривые. Уравнения Липпмана
Первые данные о строении ДЭС получены из анализа
Граница раздела двух фаз обладает избыточной свободной энергией вследствие отличия энергии частиц на поверхности раздела фаз от энергии частиц в объеме фазы.
Избыточная свободная энергия вызывает межфазное (поверхностное) натяжение (σ), которое определяют как работу образования единицы поверхности (Дж/м2 или Н/м).
Поверхностное натяжение характеризует избыток сил притяжения над силами отталкивания.
[Н]=[кг·м/с2 ] [Н/м]=[кг/с2].
Для снятия электрокапиллярных кривых Гуи предложил установку – капиллярный электрометр.
Слайд 17Капиллярный электрометр состоит из измерительной бюретки 1, емкости для ртути 2,
Положение мениска ртути в капилляре определяется, с одной стороны, высотой столба ртути в измерительной бюретке электрометра h, с другой стороны – поверхностным натяжением на границе ртуть-раствор:
πr²hρq = 2πrσ.
Отсюда следует
где ρ - плотность ртути; q - ускорение свободного падения;
r - радиус капилляра; h - высота столба ртути