- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Развертка поверхностей презентация
Содержание
- 1. Развертка поверхностей
- 2. Понятия и определения Если отсек поверхности может
- 3. Основные свойства развертки поверхностей 1. Длины двух
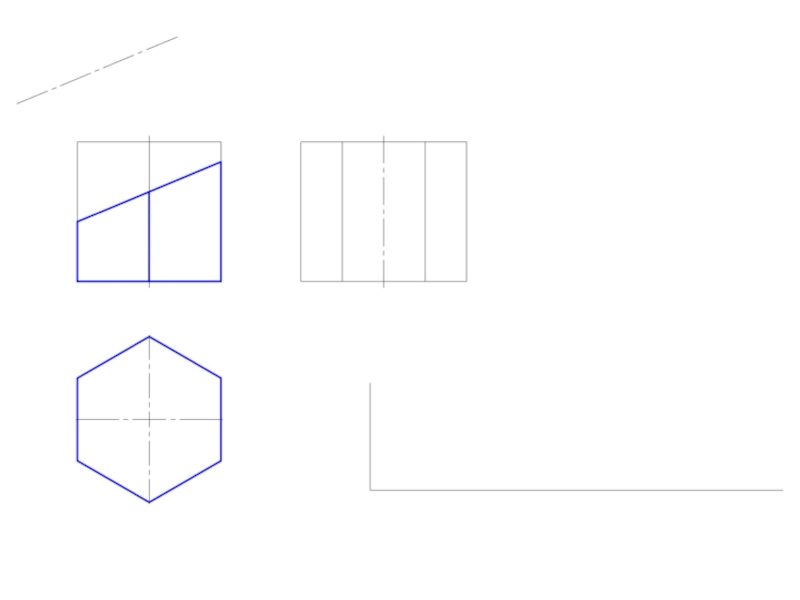
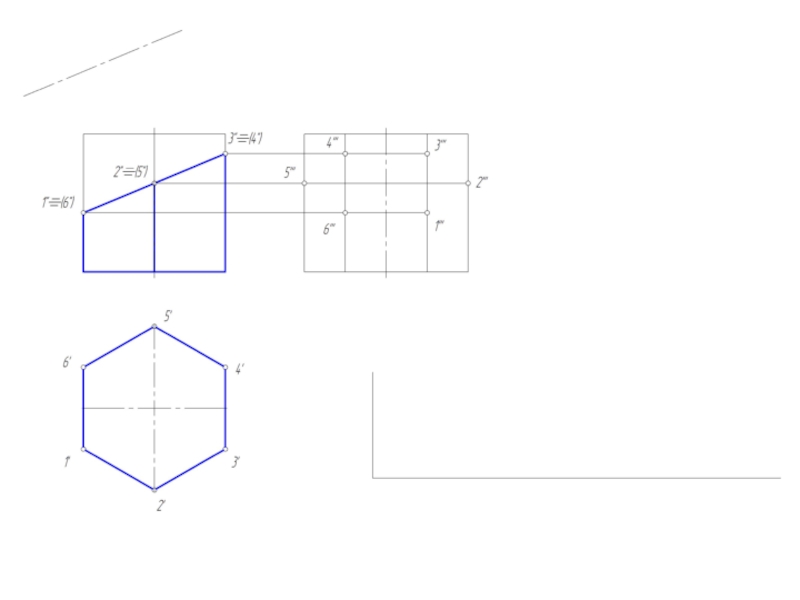
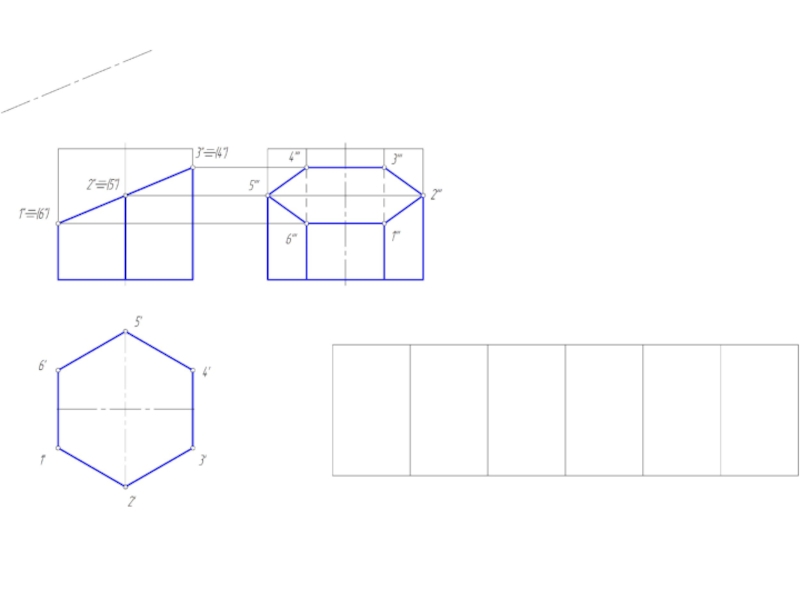
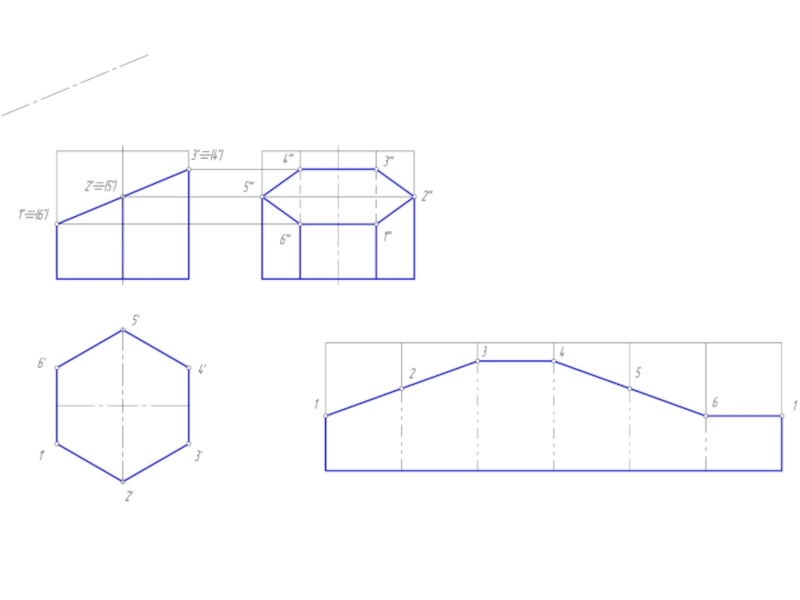
- 4. Развертка поверхности многогранников Под разверткой многогранной поверхности
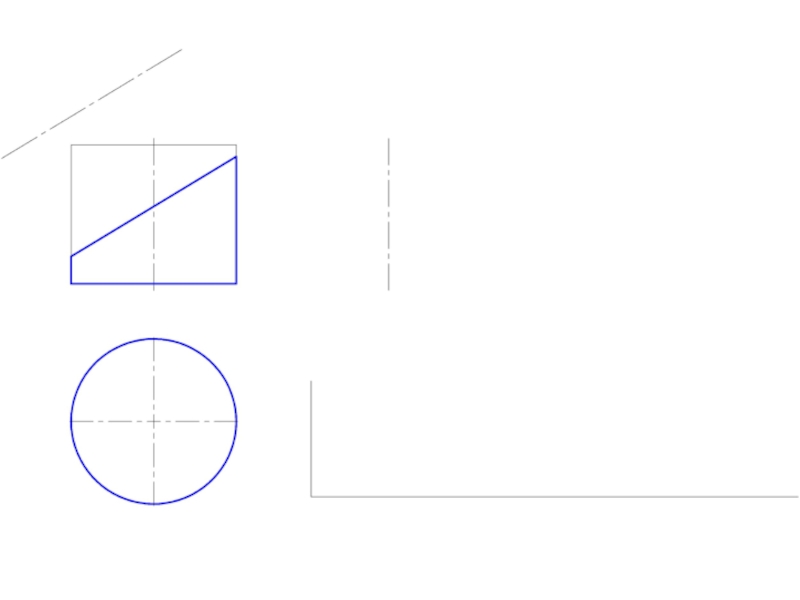
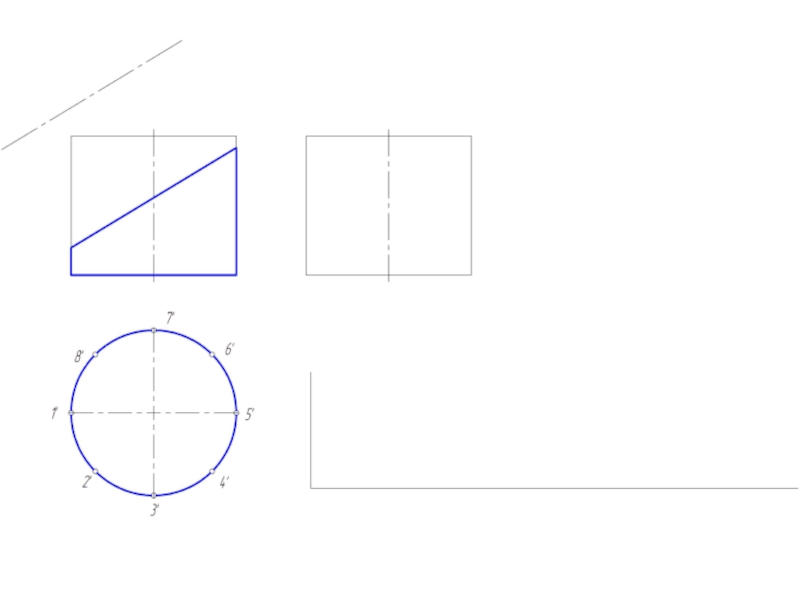
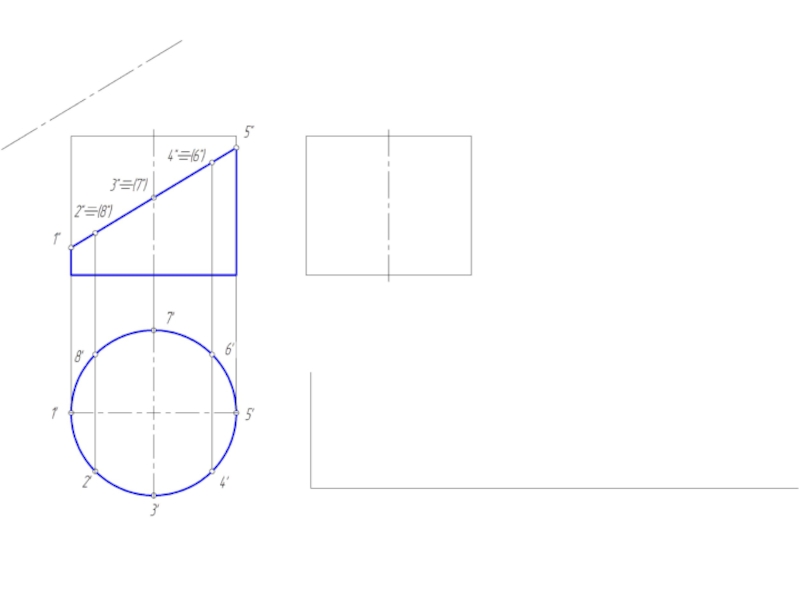
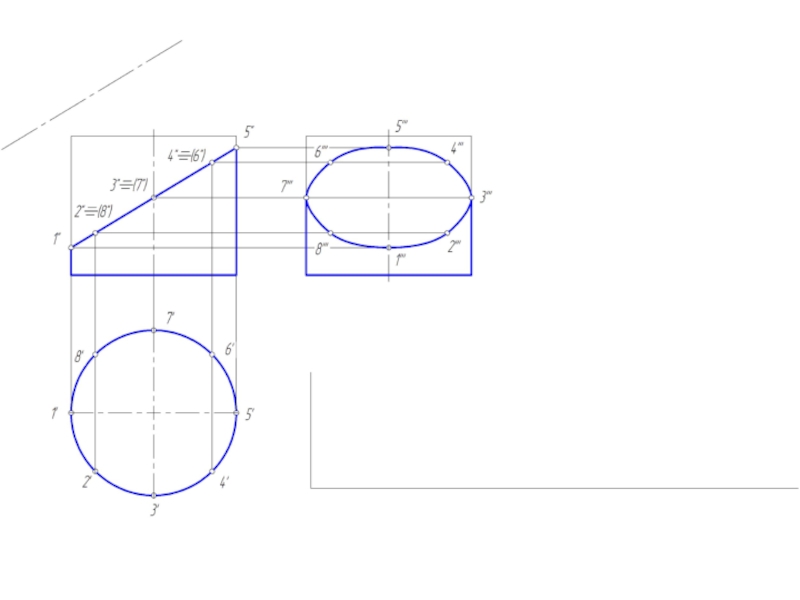
- 14. Построение развертки цилиндрической поверхности Для построения
- 26. Построение развертки конической поверхности Задача на построение
Слайд 2Понятия и определения
Если отсек поверхности может быть совмещен с плоскостью без
разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.
Поверхности, которые не могут быть совмещены с плоскостью, относятся к неразвертываемым поверхностям.
Поверхности, которые не могут быть совмещены с плоскостью, относятся к неразвертываемым поверхностям.
Слайд 3Основные свойства развертки поверхностей
1. Длины двух соответствующих линий поверхности и ее
развертки равны между собой.
2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке.
3. Прямой на поверхности соответствует также прямая на развертке.
4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке.
2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке.
3. Прямой на поверхности соответствует также прямая на развертке.
4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке.
Слайд 4Развертка поверхности многогранников
Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из
граней этой поверхности, совмещенных с одной плоскостью.
Существуют три способа построения развертки многогранных поверхностей:
1. способ нормального сечения;
2. способ раскатки;
3. способ треугольников (треангуляции).
Первых два – для развертки призматических поверхностей.
Третий – для пирамидальных поверхностей.
Существуют три способа построения развертки многогранных поверхностей:
1. способ нормального сечения;
2. способ раскатки;
3. способ треугольников (треангуляции).
Первых два – для развертки призматических поверхностей.
Третий – для пирамидальных поверхностей.
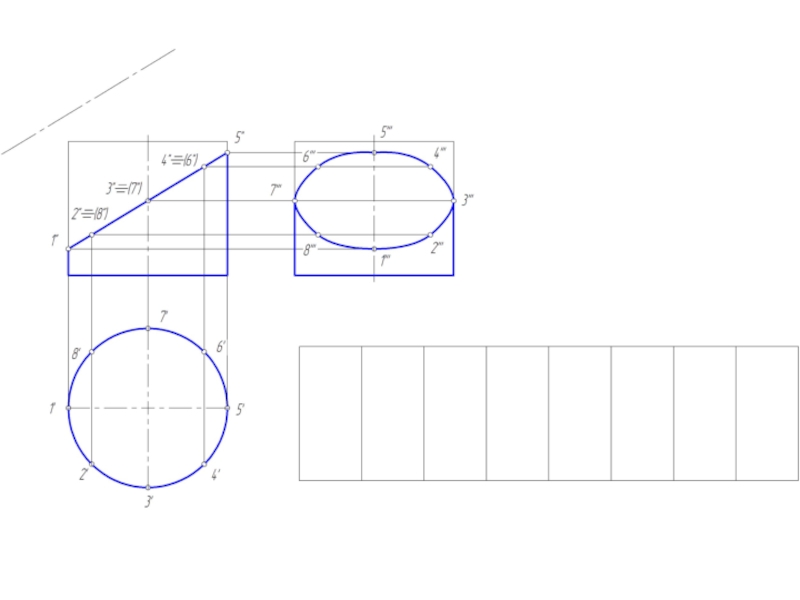
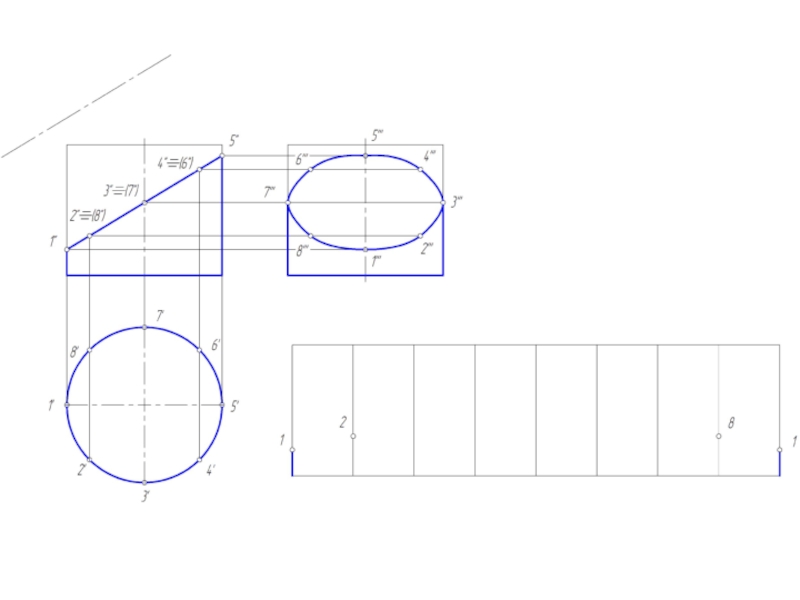
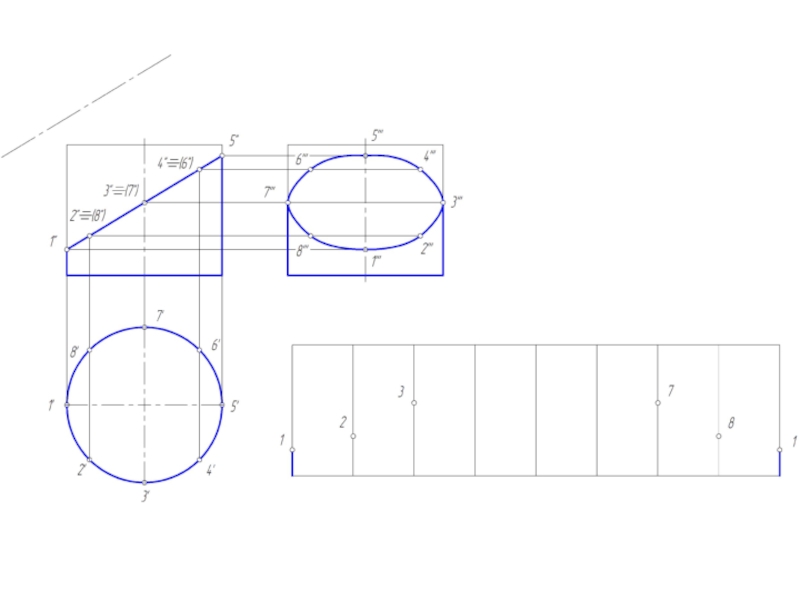
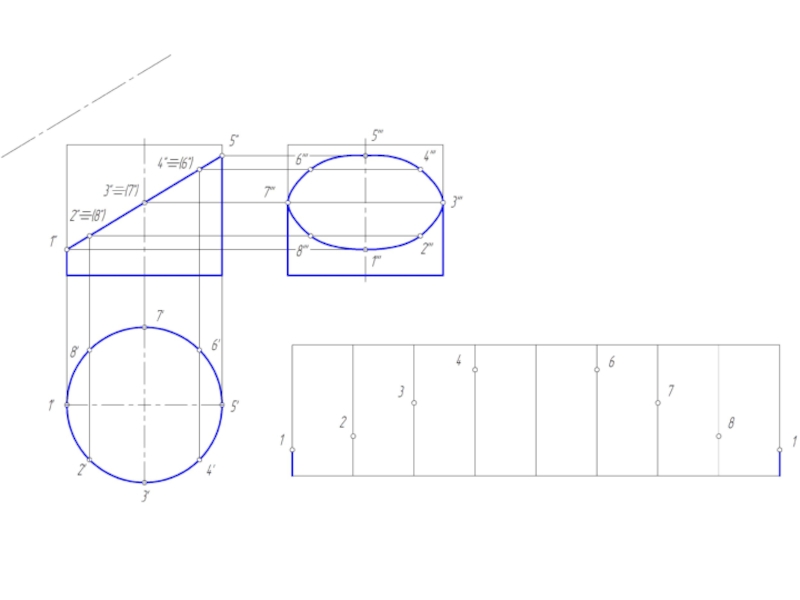
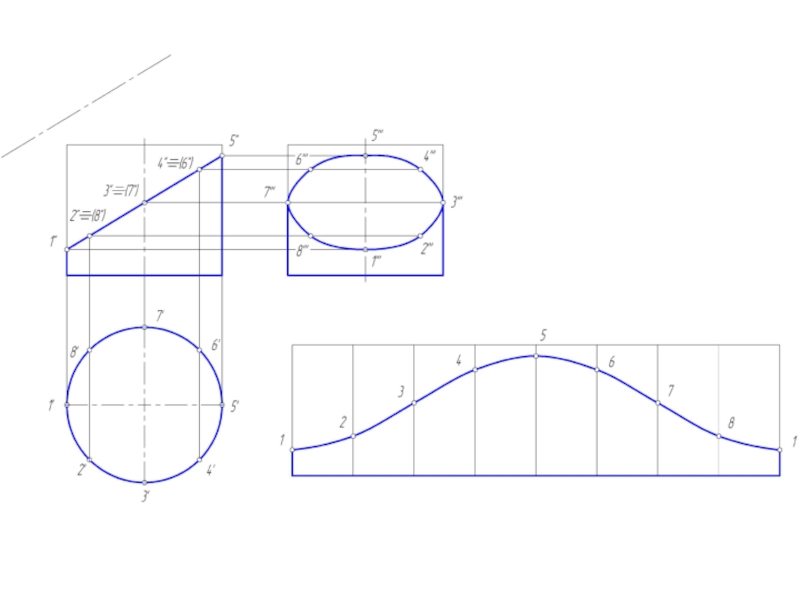
Слайд 14Построение развертки цилиндрической поверхности
Для построения развертки цилиндрической поверхности используются те же
способы нормального сечения и раскатки, которые применяются для развертки призмы.
В обоих случаях цилиндрическую поверхность заменяют (аппроксимируют) призматической поверхностью, вписанной в данную цилиндрическую поверхность.
Развертка прямого кругового цилиндра – прямоугольник, основание = развернутой окружности, а высота = высоте цилиндра.
В обоих случаях цилиндрическую поверхность заменяют (аппроксимируют) призматической поверхностью, вписанной в данную цилиндрическую поверхность.
Развертка прямого кругового цилиндра – прямоугольник, основание = развернутой окружности, а высота = высоте цилиндра.
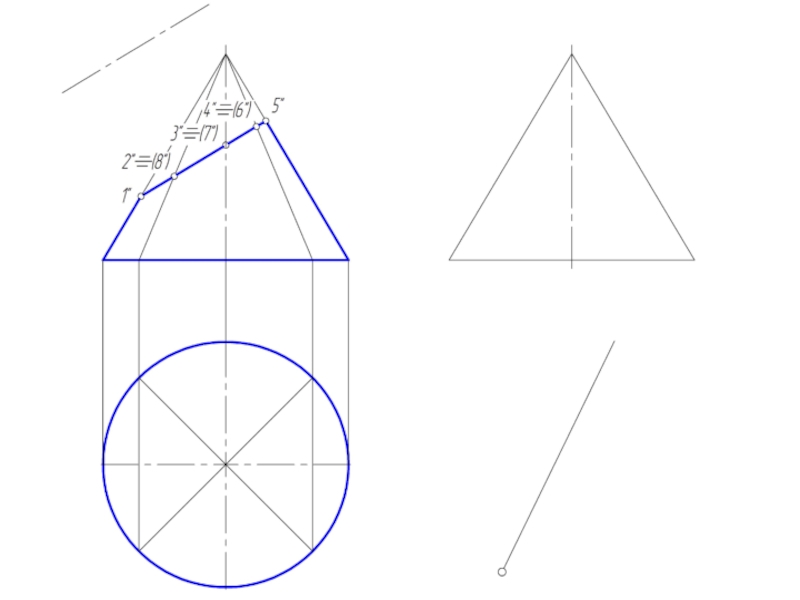
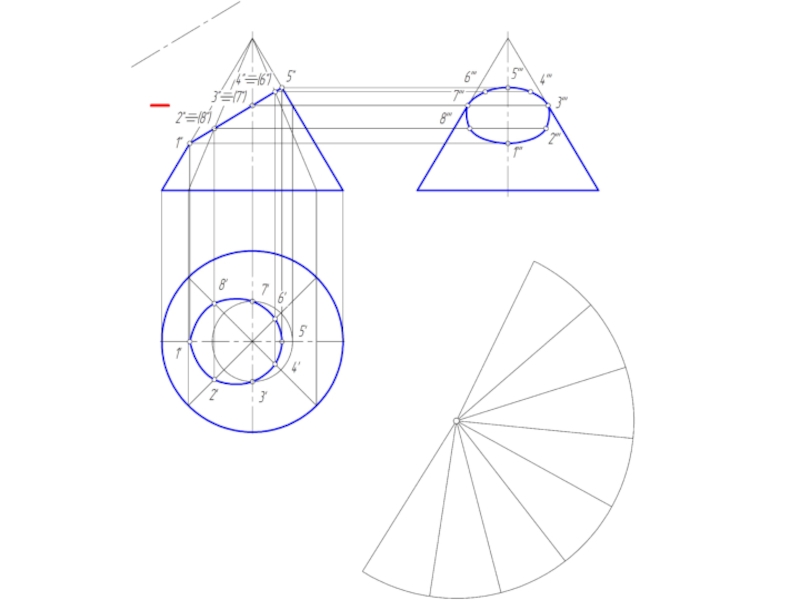
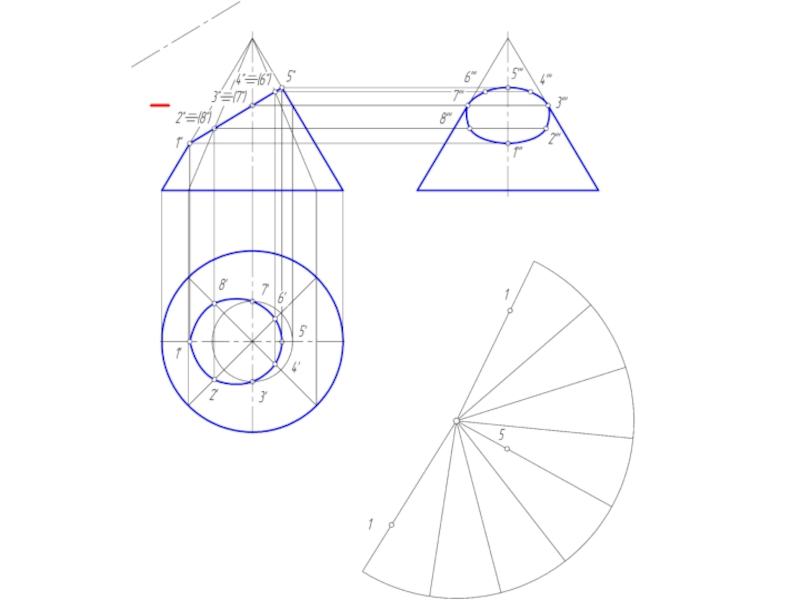
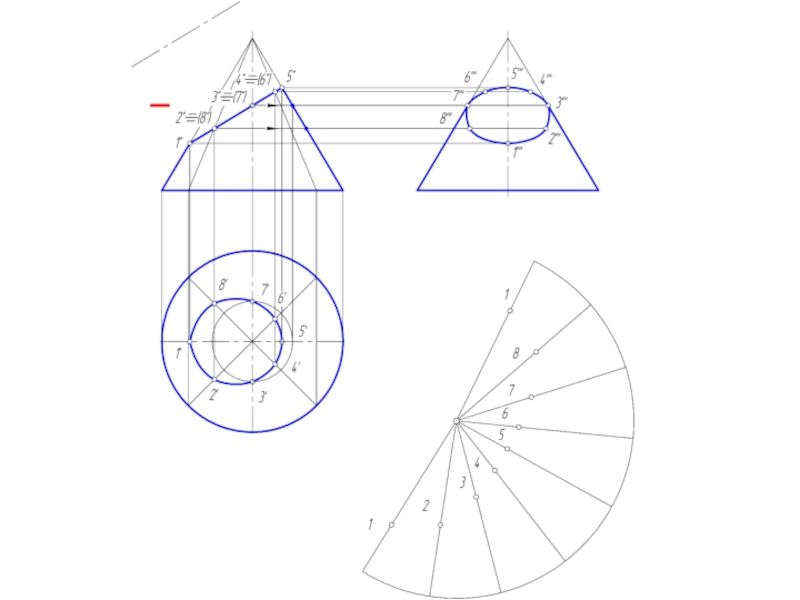
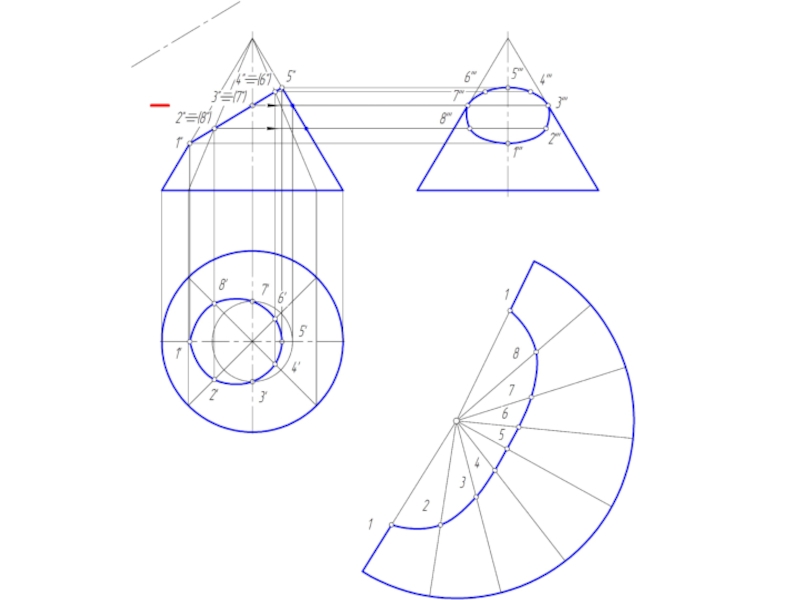
Слайд 26Построение развертки конической поверхности
Задача на построение развертки конической поверхности решается способом
треугольников. для этого коническая поверхность аппроксимируется вписанной в нее пирамидальной поверхностью.
Если задана поверхность прямого кругового конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого = длине образующей конической поверхности, а центральный угол φ = 180º R/L, где:
R – радиус окружности основания конуса;
L – длина образующей конуса.
Если задана поверхность прямого кругового конуса, то развертка его боковой поверхности представляет круговой сектор, радиус которого = длине образующей конической поверхности, а центральный угол φ = 180º R/L, где:
R – радиус окружности основания конуса;
L – длина образующей конуса.