- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проецирование плоскости презентация
Содержание
- 1. Проецирование плоскости
- 2. ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ Плоскость – неопределяемое понятие геометрии
- 3. Задание плоскости на чертеже
- 4. Следы плоскости – прямые, по которым данная
- 5. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ Признаки принадлежности:
- 6. Построение неизвестной проекции точки, принадлежащей плоскости α 1 2 3 Рис. 3.4
- 7. Теорема. Если прямая принадлежит плоскости, то проекции
- 8. ПРЯМЫЕ ЛИНИИ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ 1.
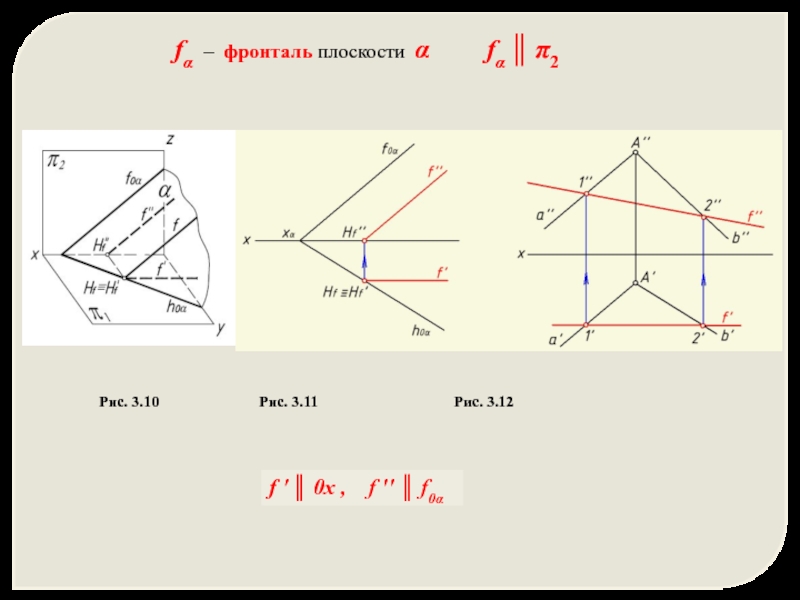
- 9. fα – фронталь плоскости α
- 10. Линии наибольшего наклона (ЛНН) плоскости к плоскостям
- 11. Рис. 3.14 Линии наибольшего наклона плоскости α
- 12. Рис. 3.15 Построение ЛНН плоскости α к
- 13. Плоскости частного положения Проецирующие плоскости:
- 14. Фронтально-проецирующая плоскость – перпендикулярна к фронтальной плоскости
- 15. Профильно-проецирующая плоскость – перпендикулярна к
- 16. 2. Плоскости уровня: Горизонтальная плоскость – параллельна
- 17. Фронтальная плоскость – параллельна фронтальной плоскости проекций
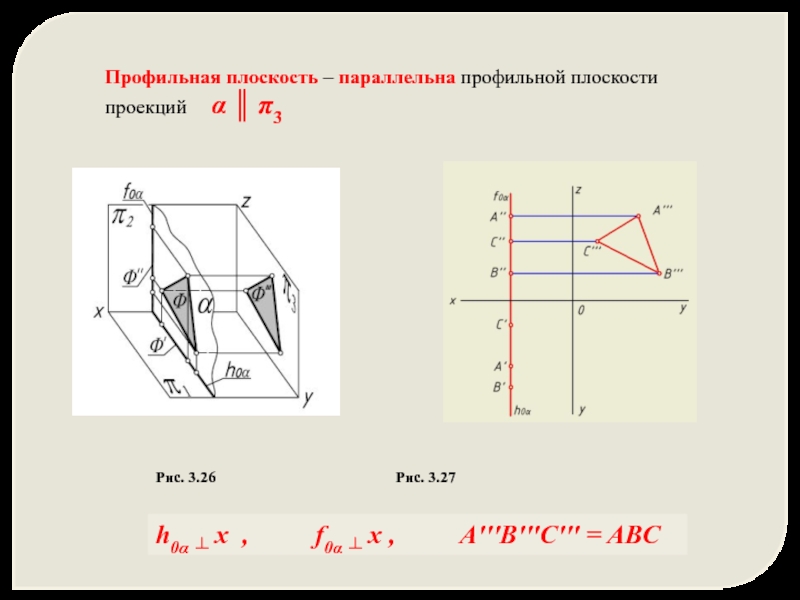
- 18. Профильная плоскость – параллельна профильной плоскости проекций
- 19. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ
- 20. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая
- 21. ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Две плоскости
- 22. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая
- 23. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Если плоскости
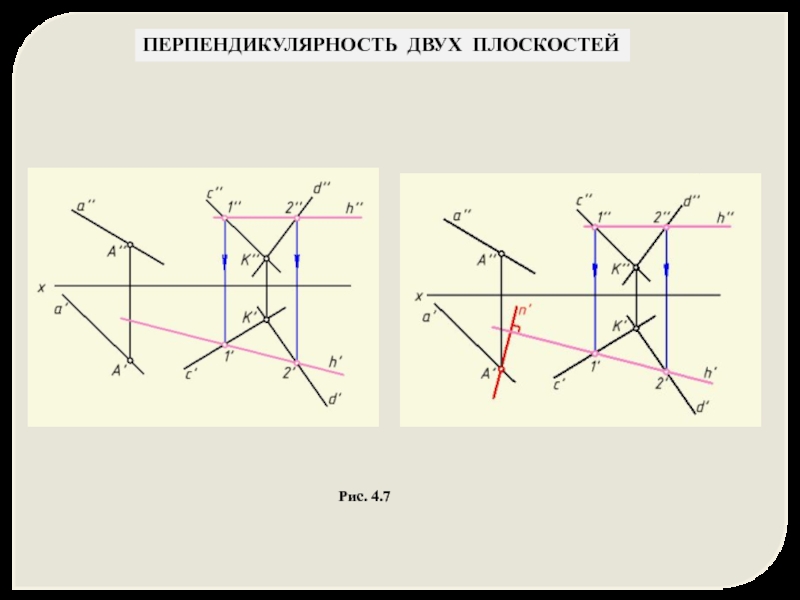
- 24. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Рис. 4.7
- 25. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Рис. 4.7 β (а
- 26. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Пример: Построить проекции плоскости,
- 27. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ Пересечение плоскостей, одна из
- 28. Пересечение плоскостей, одна из которых проецирующая Рис.
- 29. Пересечение двух плоскостей общего положения Алгоритм решения:
- 30. Пересечение двух плоскостей общего положения Рис. 4.11
- 31. Пересечение двух плоскостей общего положения Рис. 4.11
- 32. Рис. 4.11 Пересечение двух плоскостей общего положения
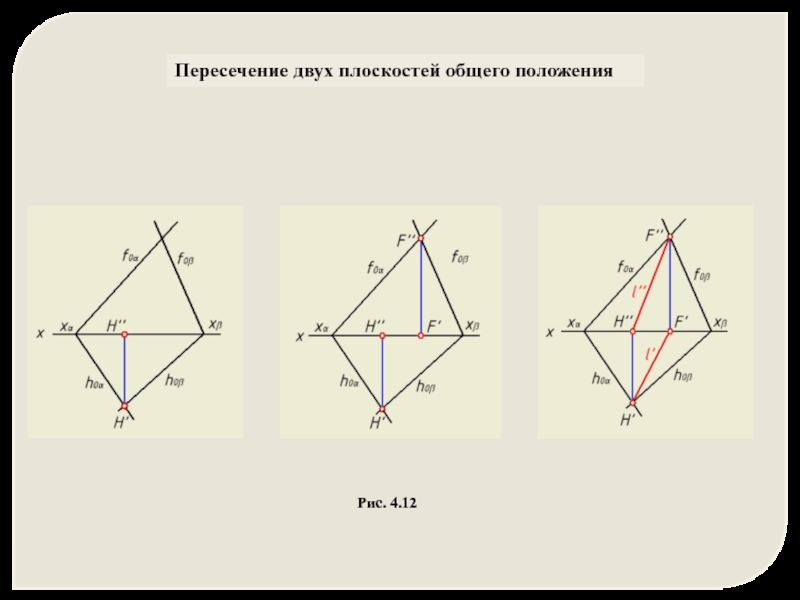
- 33. Пересечение двух плоскостей общего положения Рис. 4.12
- 34. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ 1. Пересечение прямой
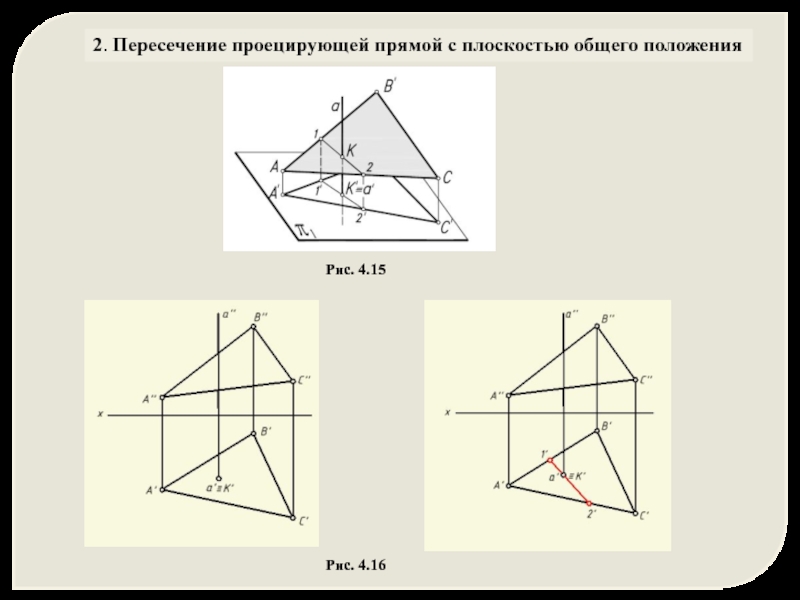
- 35. 2. Пересечение проецирующей прямой с плоскостью общего положения Рис. 4.15 Рис. 4.16
- 36. 2. Пересечение проецирующей прямой с плоскостью общего
- 37. Пересечение прямой общего положения с плоскостью общего
- 38. Задача. Построить проекции точки пересечения прямой
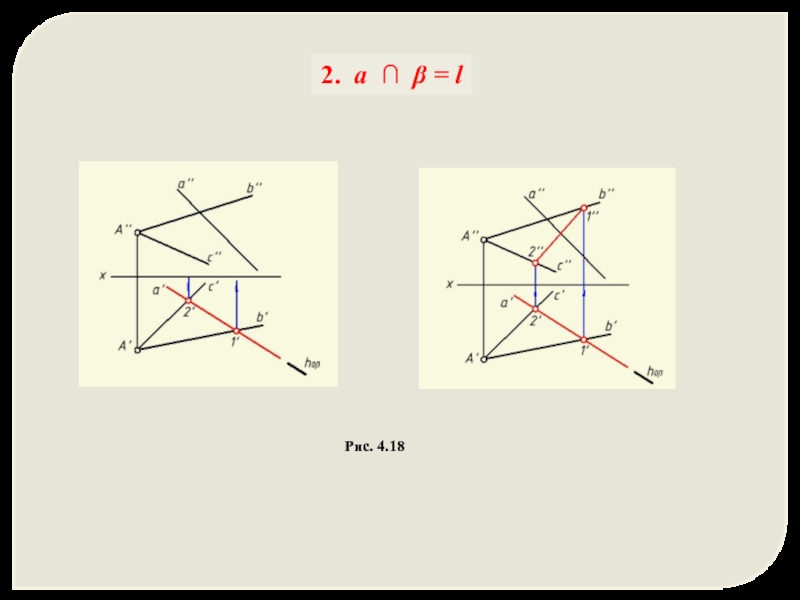
- 39. 2. a ∩ β = l Рис. 4.18
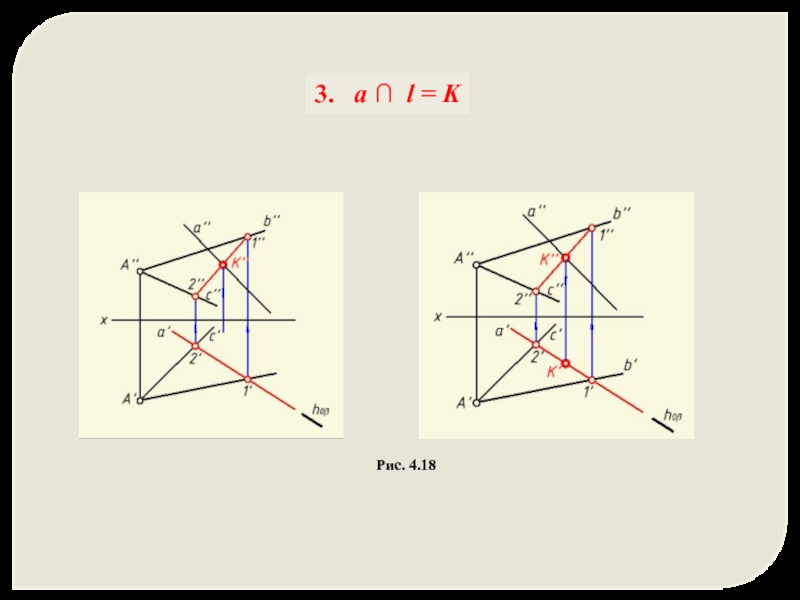
- 40. Рис. 4.18 3. a ∩ l = K
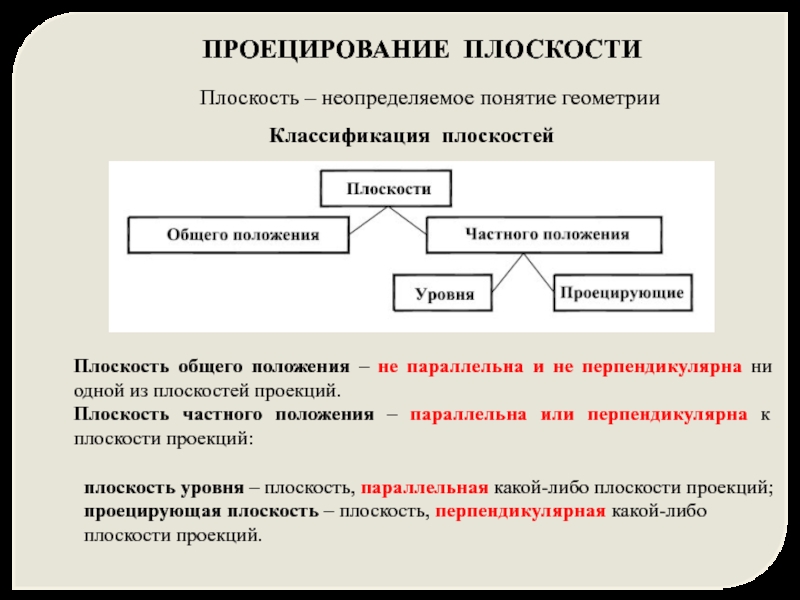
Слайд 2ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ
Плоскость – неопределяемое понятие геометрии
Плоскость общего положения – не параллельна
Плоскость частного положения – параллельна или перпендикулярна к плоскости проекций:
плоскость уровня – плоскость, параллельная какой-либо плоскости проекций;
проецирующая плоскость – плоскость, перпендикулярная какой-либо
плоскости проекций.
Классификация плоскостей
Слайд 3
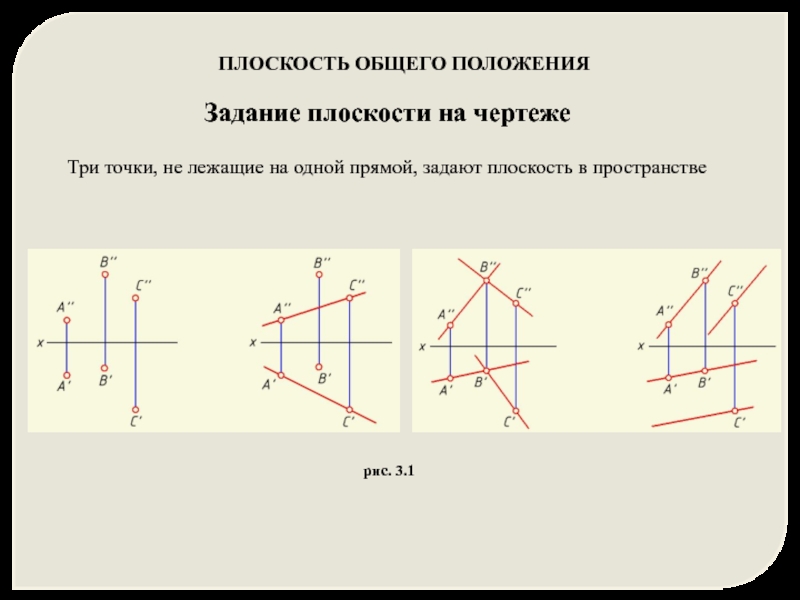
Задание плоскости на чертеже
Три точки, не лежащие на одной прямой, задают
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
рис. 3.1
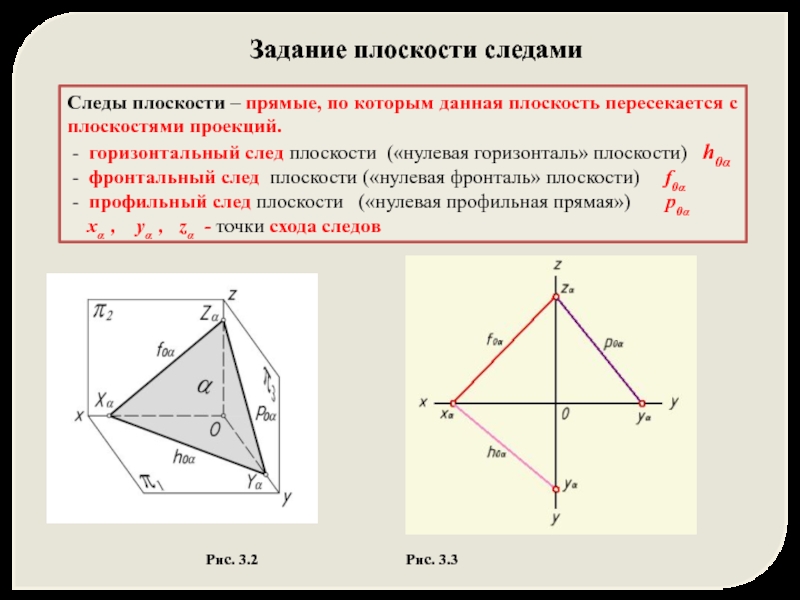
Слайд 4Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями
- горизонтальный след плоскости («нулевая горизонталь» плоскости) h0α
- фронтальный след плоскости («нулевая фронталь» плоскости) f0α
- профильный след плоскости («нулевая профильная прямая») p0α
xα , yα , zα - точки схода следов
Задание плоскости следами
Рис. 3.2 Рис. 3.3
Слайд 5ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ
Признаки принадлежности:
Теорема. Если точка принадлежит плоскости, то
одноименным проекциям прямой, лежащей в этой плоскости.
A α < = > A' lα' ᴧ A'' lα''
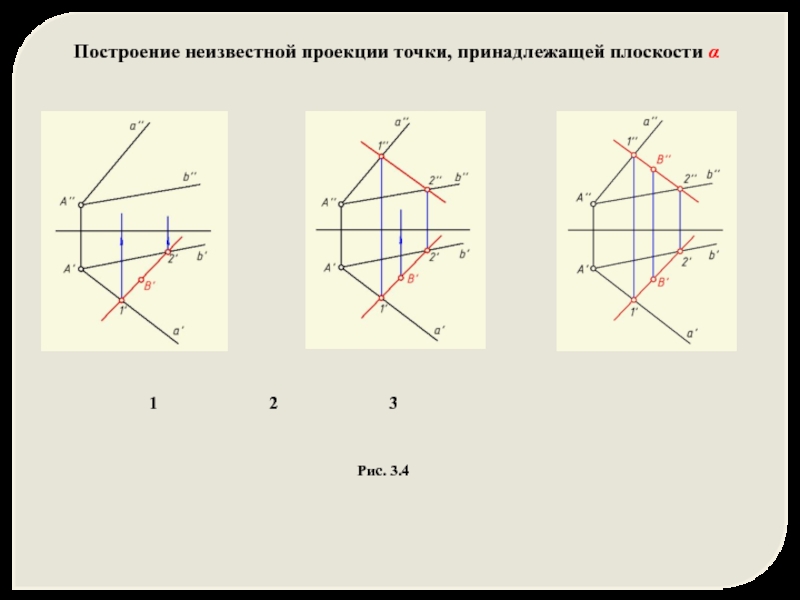
План решения:
Провести через заданную проекцию точки одноименную проекцию вспомогательной прямой l , принадлежащей данной плоскости.
Построить вторую проекцию вспомогательной прямой l .
Найти недостающую проекцию точки на основании инвариантного свойства ортогонального проецирования.
Рис. 3.4
Построение неизвестной проекции точки, принадлежащей плоскости α
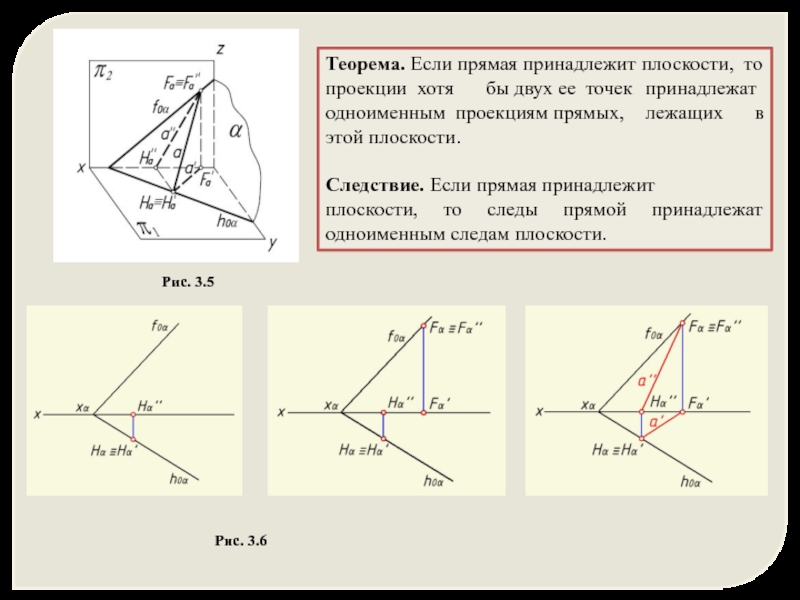
Слайд 7Теорема. Если прямая принадлежит плоскости, то проекции хотя бы двух ее
Следствие. Если прямая принадлежит плоскости, то следы прямой принадлежат одноименным следам плоскости.
Рис. 3.6
Рис. 3.5
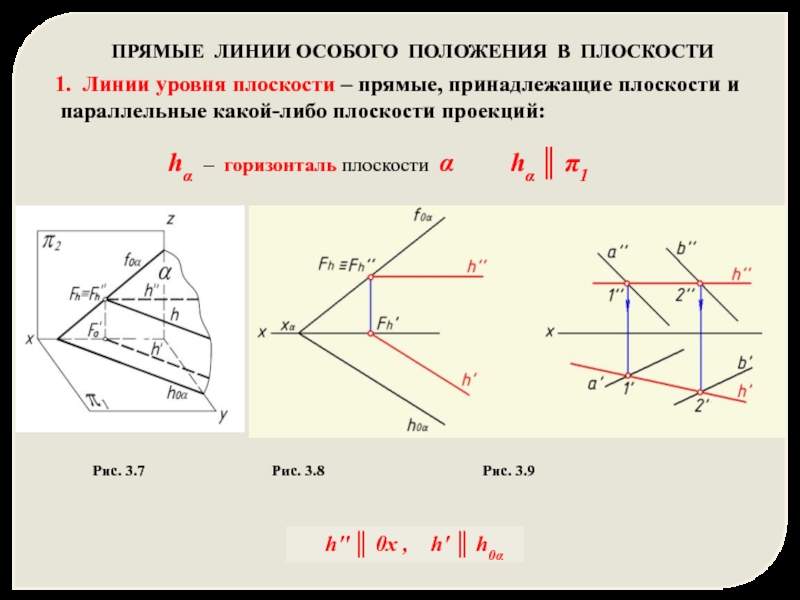
Слайд 8ПРЯМЫЕ ЛИНИИ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
1. Линии уровня плоскости – прямые,
параллельные какой-либо плоскости проекций:
hα – горизонталь плоскости α hα ║ π1
h'' ║ 0x , h' ║ h0α
Рис. 3.7 Рис. 3.8 Рис. 3.9
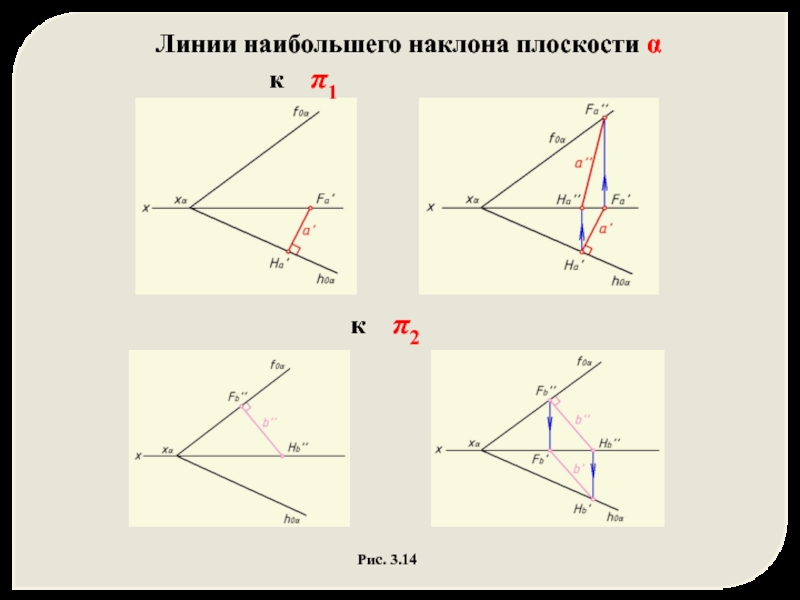
Слайд 10Линии наибольшего наклона (ЛНН) плоскости к плоскостям проекций – прямые, принадлежащие
- линия наибольшего наклона плоскости α к горизонтальной плоскости проекций (линия ската) перпендикулярна к горизонтали плоскости α a ┴ hα
- линия наибольшего наклона плоскости α к фронтальной плоскости проекций перпендикулярна к фронтали плоскости α b ┴ fα
Линии наибольшего наклона используются для определения двугранных углов между заданной плоскостью и соответствующей плоскостью проекций.
ПРЯМЫЕ ЛИНИИ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
ПРАВИЛО определения угла наклона заданной плоскости к плоскости проекций
Провести линию наибольшего наклона (ЛНН) перпендикулярно к одноименной линии уровня плоскости.
Определить угол наклона построенной ЛНН к выбранной плоскости проекций (см. правило определения длины отрезка прямой).
Построенный угол для ЛНН равен углу наклона самой данной плоскости к выбранной плоскости проекций.
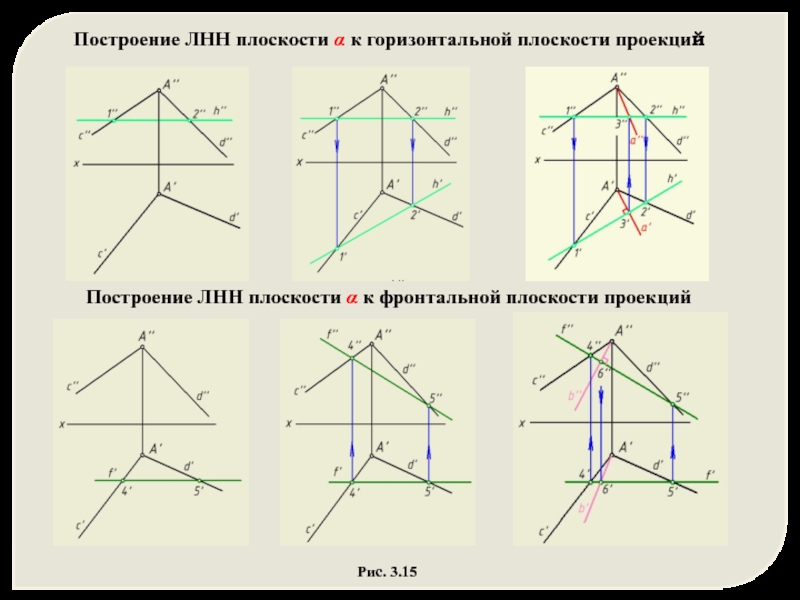
Слайд 12Рис. 3.15
Построение ЛНН плоскости α к фронтальной плоскости проекций
Построение ЛНН плоскости
Слайд 13Плоскости частного положения
Проецирующие плоскости:
Горизонтально-проецирующая плоскость – перпендикулярна к горизонтальной плоскости проекций
Рис. 3.16 Рис. 3.17
f0α ┴ x β = α^π2 A' , a' , Ф' h0α
Слайд 14Фронтально-проецирующая плоскость – перпендикулярна к фронтальной плоскости проекций α ┴
Рис. 3.18 Рис. 3.19
h0α ┴ 0x α = α^π1 A'' , a'' , Ф'' f0α
Слайд 15
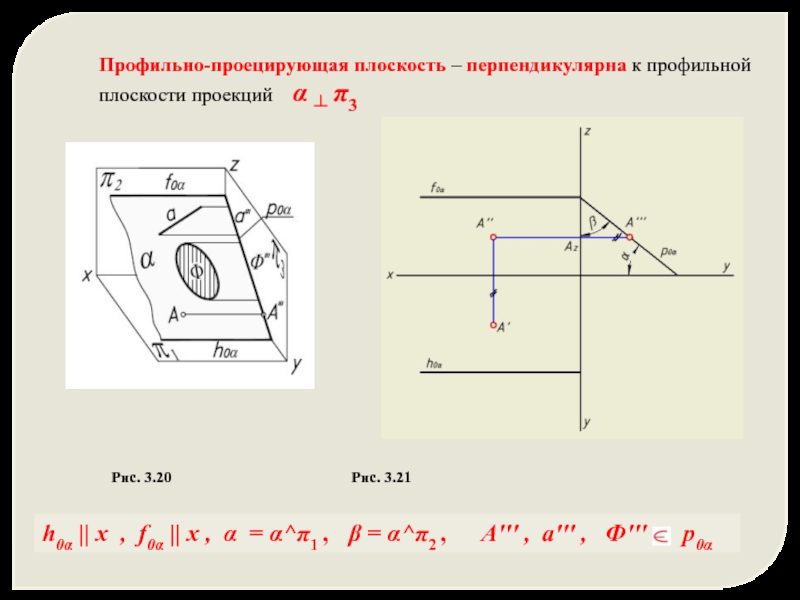
Профильно-проецирующая плоскость – перпендикулярна к профильной плоскости проекций α ┴
Рис. 3.20 Рис. 3.21
h0α || x , f0α || x , α = α^π1 , β = α^π2 , A''' , a''' , Ф''' p0α
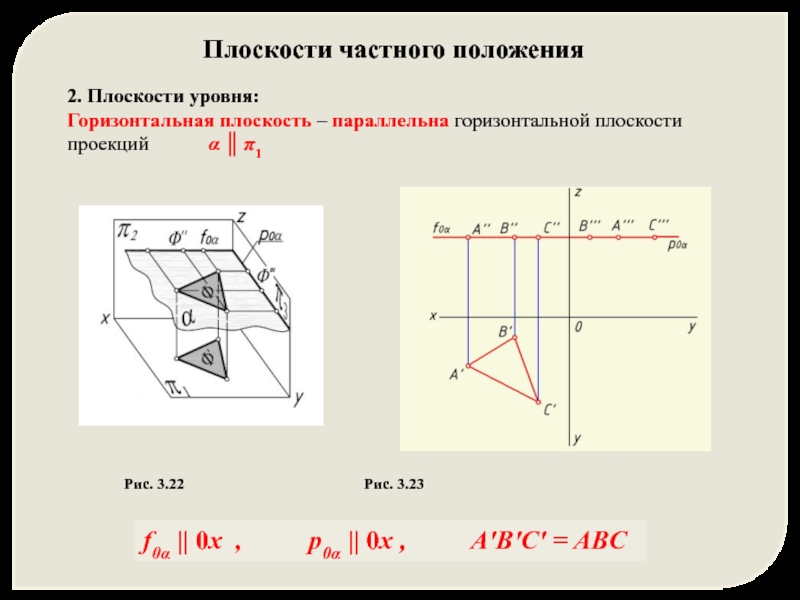
Слайд 162. Плоскости уровня:
Горизонтальная плоскость – параллельна горизонтальной плоскости проекций
Плоскости частного положения
Рис. 3.22 Рис. 3.23
f0α || 0x , p0α || 0x , A'B'C' = ABC
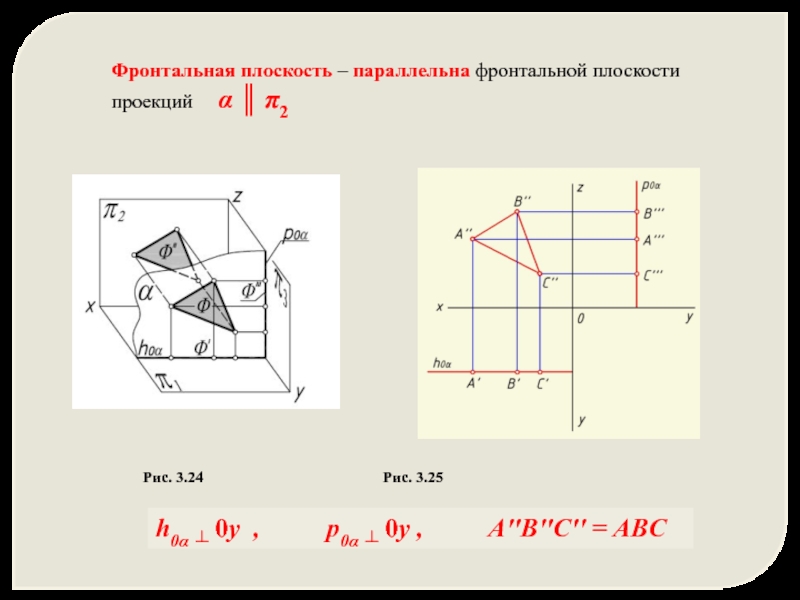
Слайд 17Фронтальная плоскость – параллельна фронтальной плоскости проекций α ║
Рис. 3.24 Рис. 3.25
h0α ┴ 0y , p0α ┴ 0y , A''B''C'' = ABC
Слайд 18Профильная плоскость – параллельна профильной плоскости проекций α ║
Рис. 3.26 Рис. 3.27
h0α ┴ x , f0α ┴ x , A'''B'''C''' = ABC
Слайд 20ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ТЕОРЕМА. Если прямая параллельна плоскости, то проекции данной
a ║ α < = > a' ║ lα ' ᴧ a'' ║ lα ''
a ║ α (h, f) , b α < = > a' ║ b ' ᴧ a'' ║ b ''
Слайд 21ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ
ТЕОРЕМА. Две плоскости параллельны, если проекции двух пересекающихся
СЛЕДСТВИЕ. Если две плоскости параллельны, то их одноименные следы параллельны
Рис. 4.1 Рис. 4.2
α (a ∩ b) ║ β (c ∩ d) < = > a' ║ c' , b' ║ d' ᴧ a''║ c'' , b'' ║ d''
α ║ β < = > h0α ║ h0β ᴧ f0α ║ f0β
Слайд 22ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ТЕОРЕМА. Если прямая перпендикулярна плоскости, то горизонтальная проекция
прямой
n ┴ α(h, f) < = > n' ┴ h' ᴧ n'' ┴ f ''
В общем случае отношение перпендикулярности в пространстве не сохраняет признаков перпендикулярности на чертеже.
Пример: Построить проекции прямой, перпендикулярной к заданной плоскости
и проходящей через точку A.
Рис. 4.3 Рис. 4.4 Рис. 4.5
Слайд 23ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
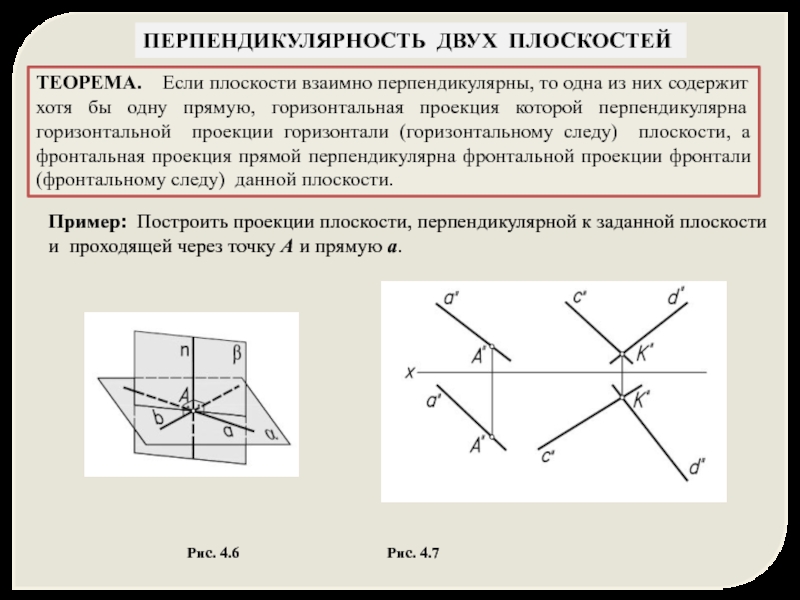
ТЕОРЕМА. Если плоскости взаимно перпендикулярны, то одна из
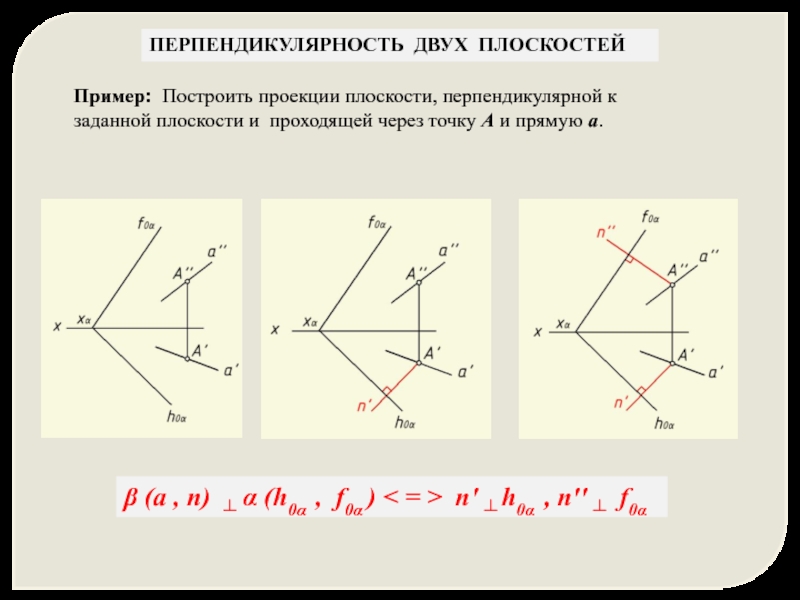
Пример: Построить проекции плоскости, перпендикулярной к заданной плоскости и проходящей через точку A и прямую a.
Рис. 4.6 Рис. 4.7
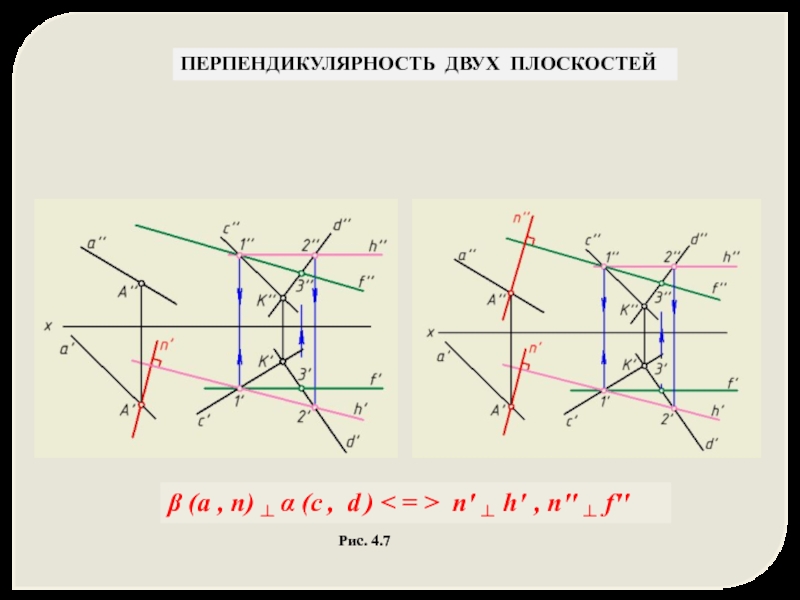
Слайд 26ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
Пример: Построить проекции плоскости, перпендикулярной к заданной плоскости и
β (а , n) ┴ α (h0α , f0α ) < = > n' ┴ h0α , n'' ┴ f0α
Слайд 27ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
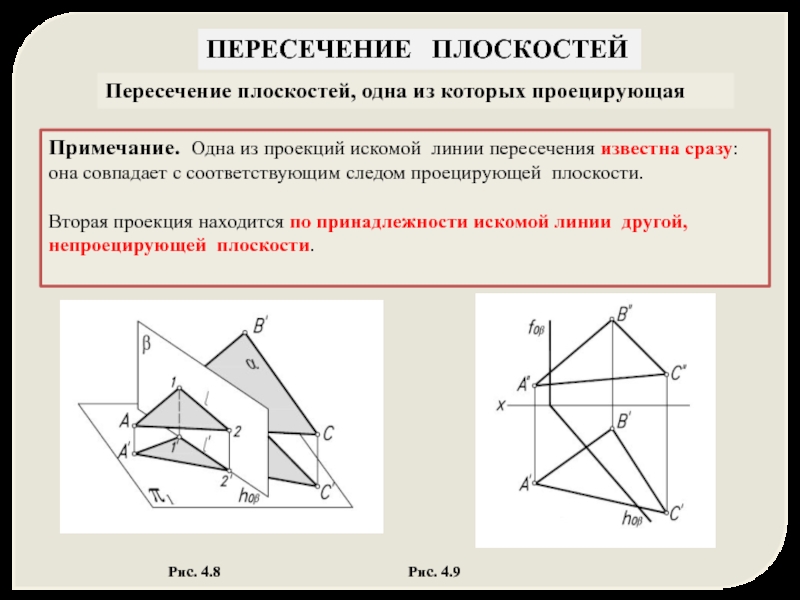
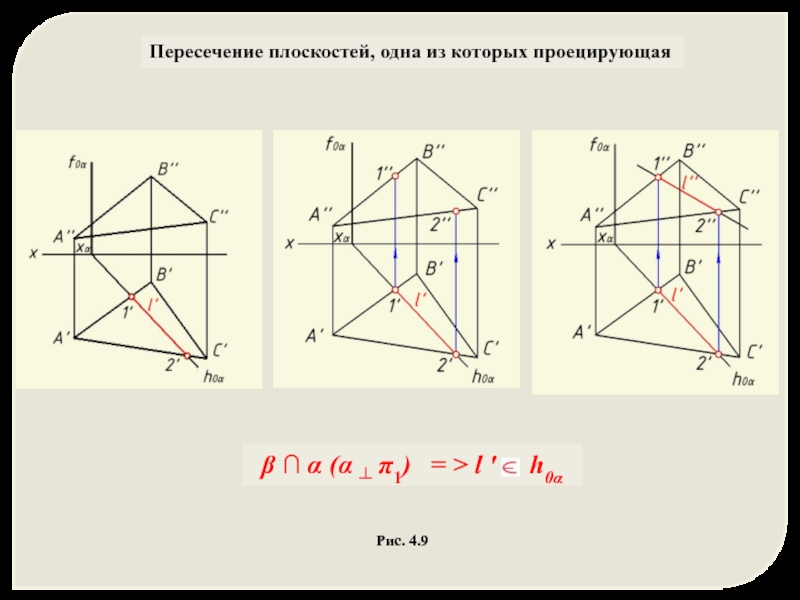
Пересечение плоскостей, одна из которых проецирующая
Примечание. Одна из проекций
Вторая проекция находится по принадлежности искомой линии другой,
непроецирующей плоскости.
Рис. 4.8 Рис. 4.9
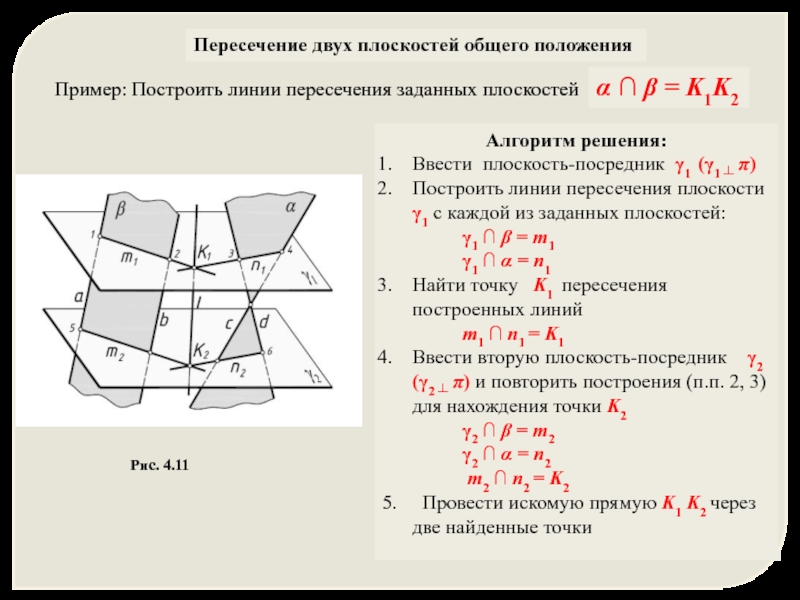
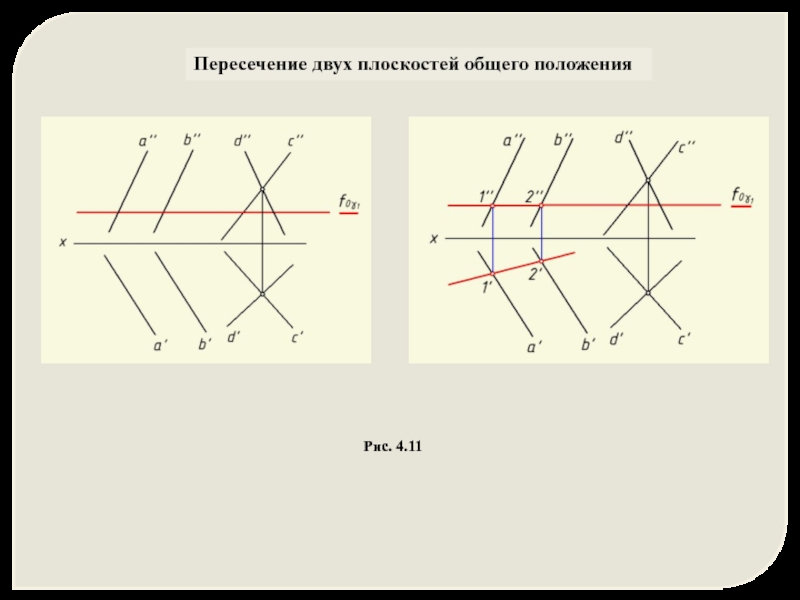
Слайд 29Пересечение двух плоскостей общего положения
Алгоритм решения:
Ввести плоскость-посредник γ1 (γ1 ┴ π)
Построить
γ1 ∩ β = m1
γ1 ∩ α = n1
Найти точку K1 пересечения построенных линий
m1 ∩ n1 = K1
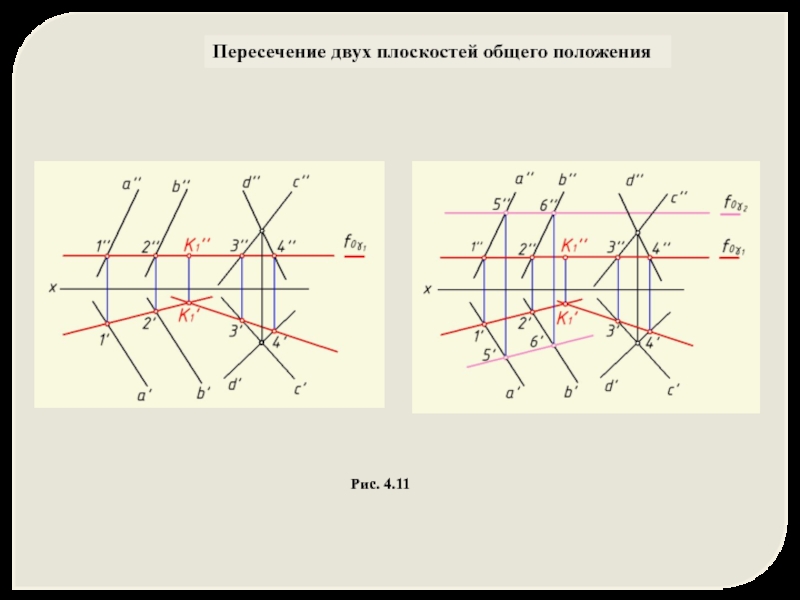
Ввести вторую плоскость-посредник γ2 (γ2 ┴ π) и повторить построения (п.п. 2, 3) для нахождения точки K2
γ2 ∩ β = m2
γ2 ∩ α = n2
m2 ∩ n2 = K2
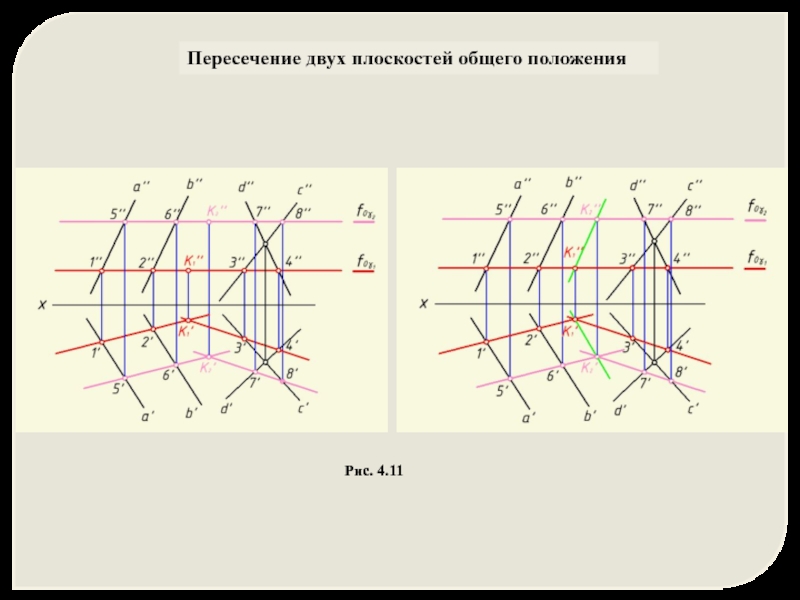
5. Провести искомую прямую K1 K2 через две найденные точки
Пример: Построить линии пересечения заданных плоскостей
α ∩ β = K1K2
Рис. 4.11
Слайд 34ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
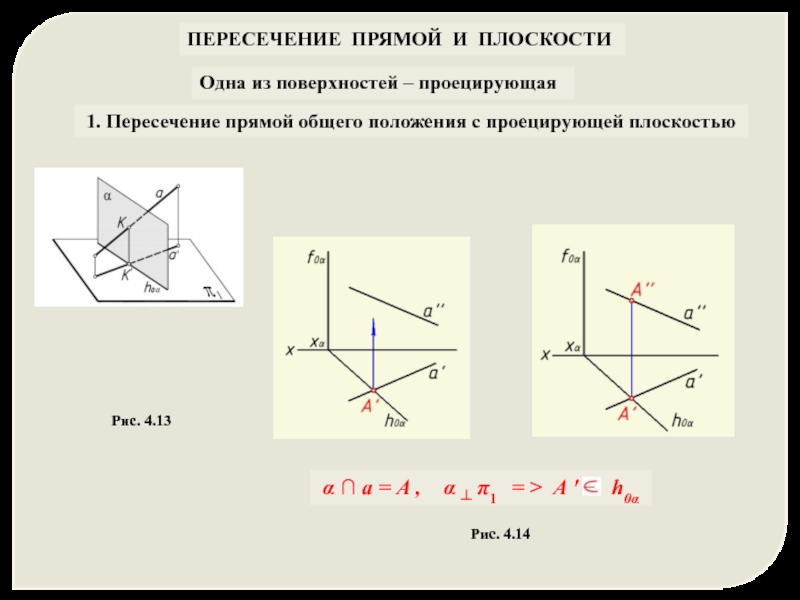
1. Пересечение прямой общего положения с проецирующей плоскостью
Одна
Рис. 4.13
Рис. 4.14
α ∩ а = A , α ┴ π1 = > A ' h0α
Слайд 362. Пересечение проецирующей прямой с плоскостью общего положения
Рис. 4.16
α ∩ а
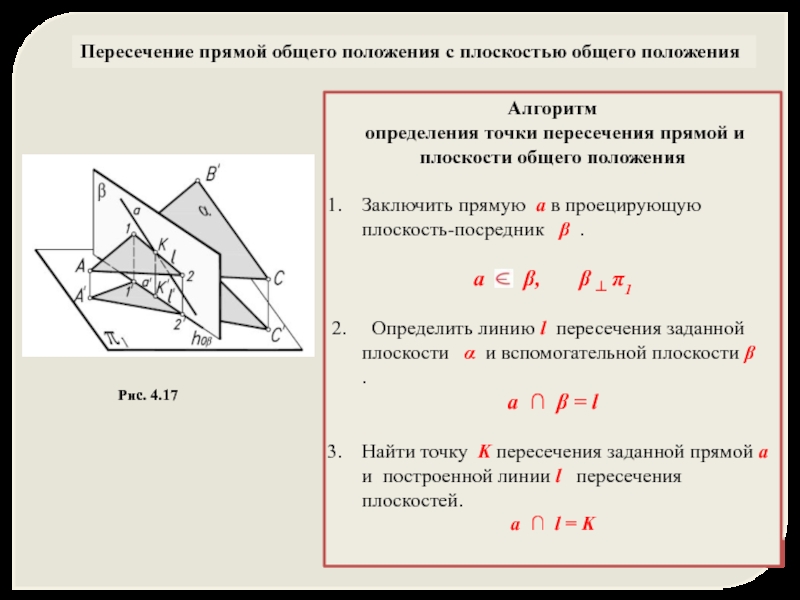
Слайд 37Пересечение прямой общего положения с плоскостью общего положения
Алгоритм
определения точки пересечения
Заключить прямую a в проецирующую плоскость-посредник β .
а β, β ┴ π1
2. Определить линию l пересечения заданной плоскости α и вспомогательной плоскости β .
a ∩ β = l
Найти точку K пересечения заданной прямой a и построенной линии l пересечения плоскостей.
a ∩ l = K
Рис. 4.17
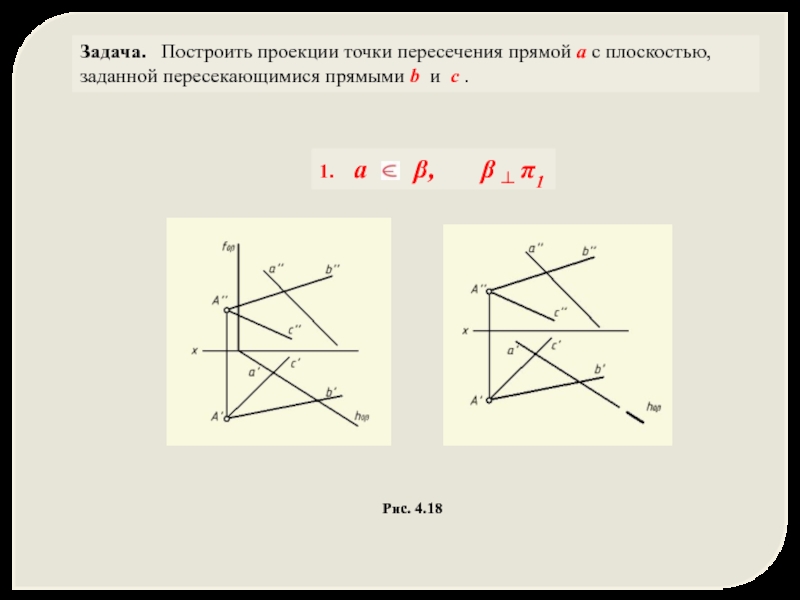
Слайд 38Задача. Построить проекции точки пересечения прямой а с плоскостью, заданной
Рис. 4.18
1. а β, β ┴ π1