- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности вращения. Основные понятия и определения презентация
Содержание
- 1. Поверхности вращения. Основные понятия и определения
- 2. http://incampus.ru/campus.aspx?id=9768998 http://egf.tti.sfedu.ru/departments/graphics/staff/staff_56.html Калашникова Татьяна Григорьевна
- 3. Основные понятия и определения Поверхности вращения
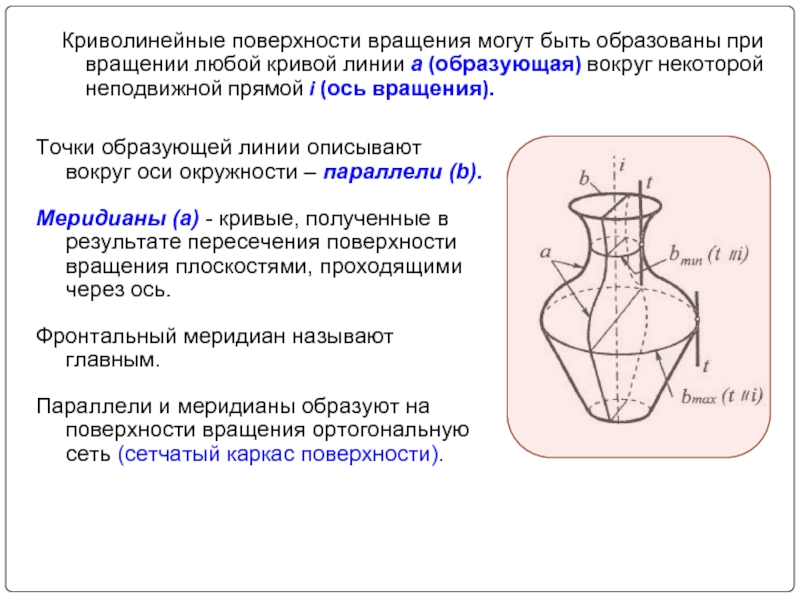
- 4. Криволинейные поверхности вращения могут быть образованы при
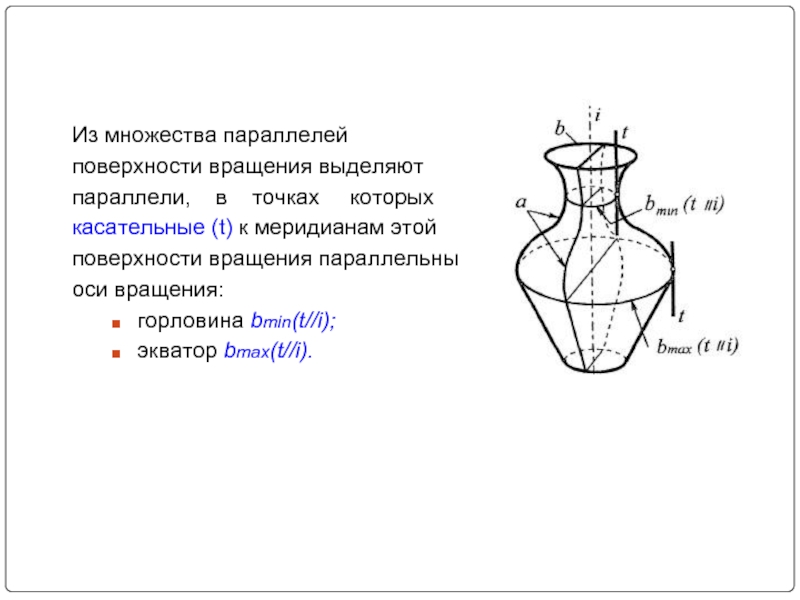
- 5. Из множества параллелей поверхности вращения выделяют параллели,
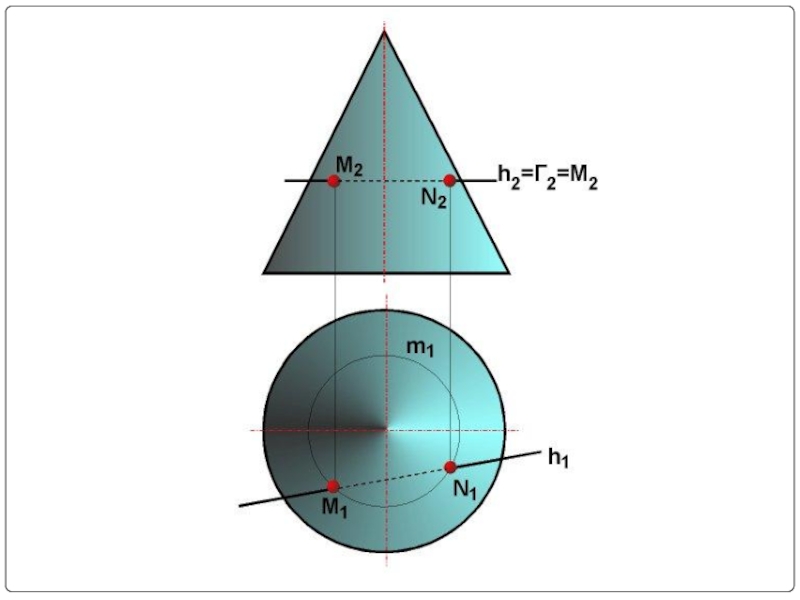
- 6. Основные свойства поверхности вращения: Любая меридиональная
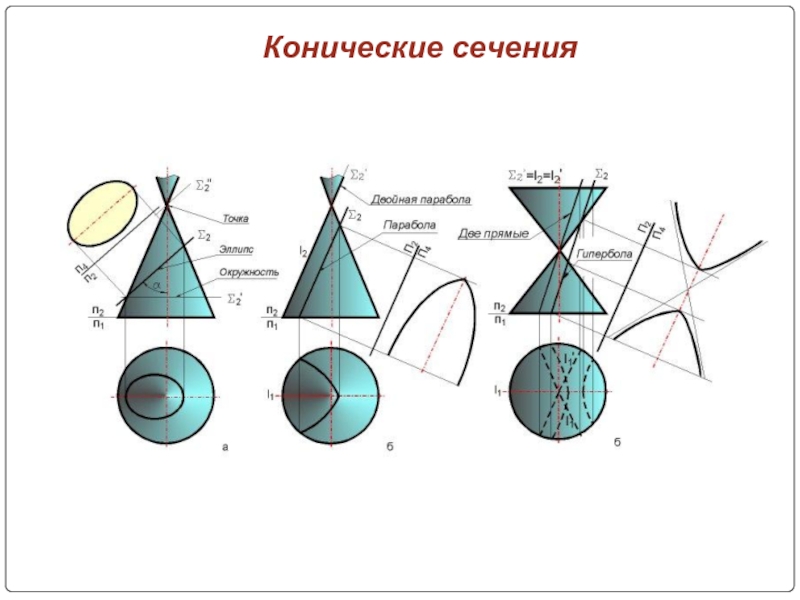
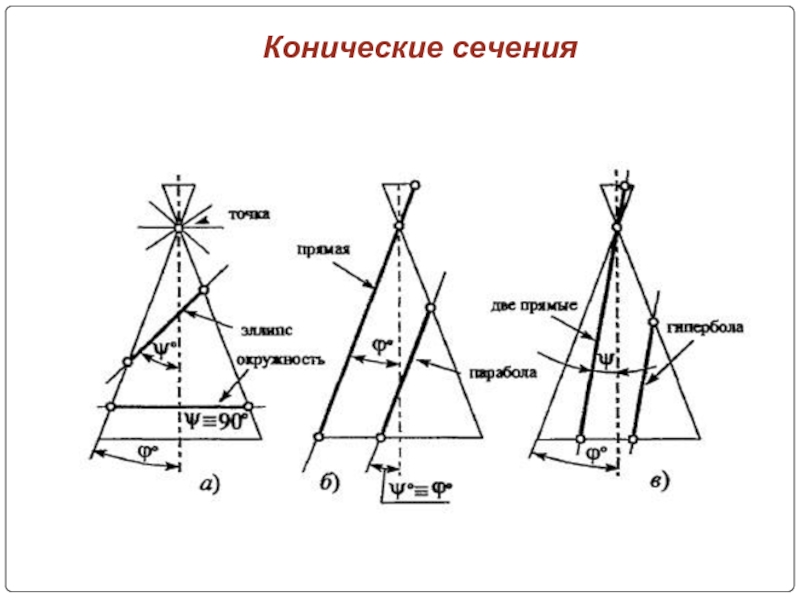
- 7. Конические сечения
- 8. Конические сечения
- 9. Конические сечения
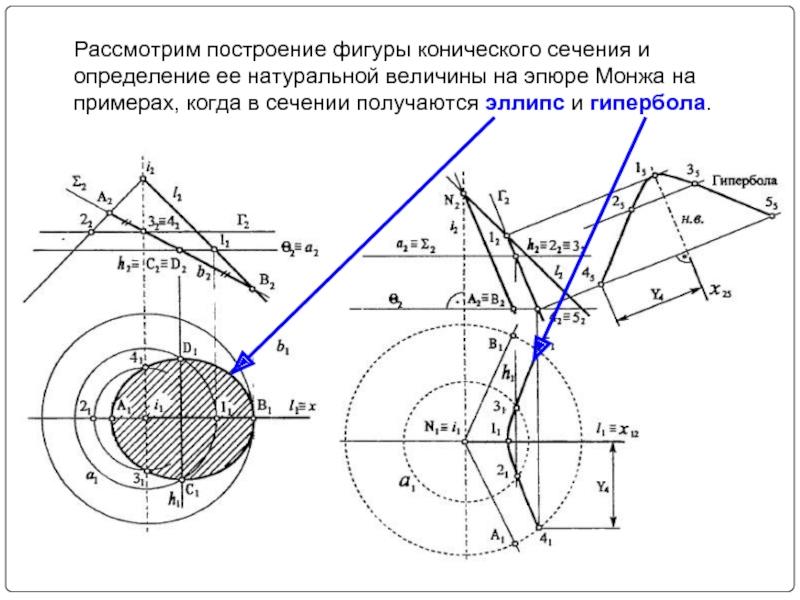
- 10. Рассмотрим построение фигуры конического сечения и определение
- 13. Конические сечения построение на эпюре
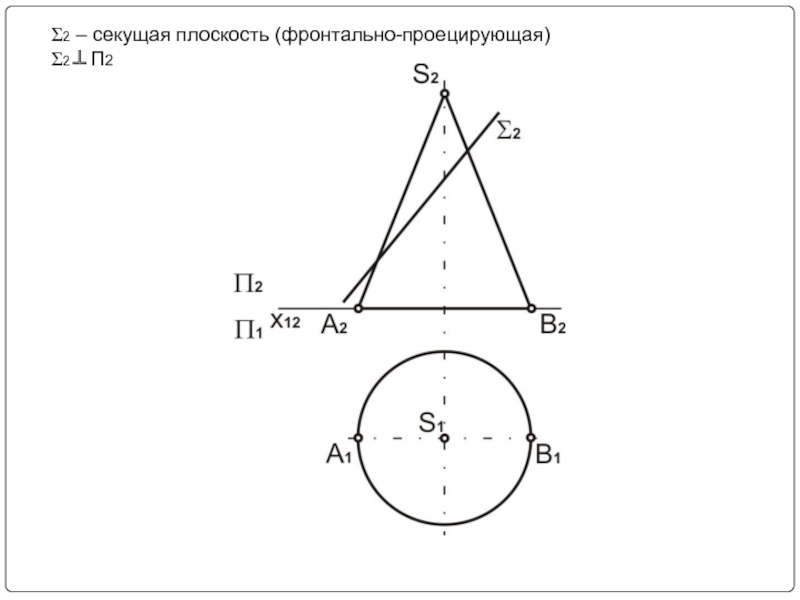
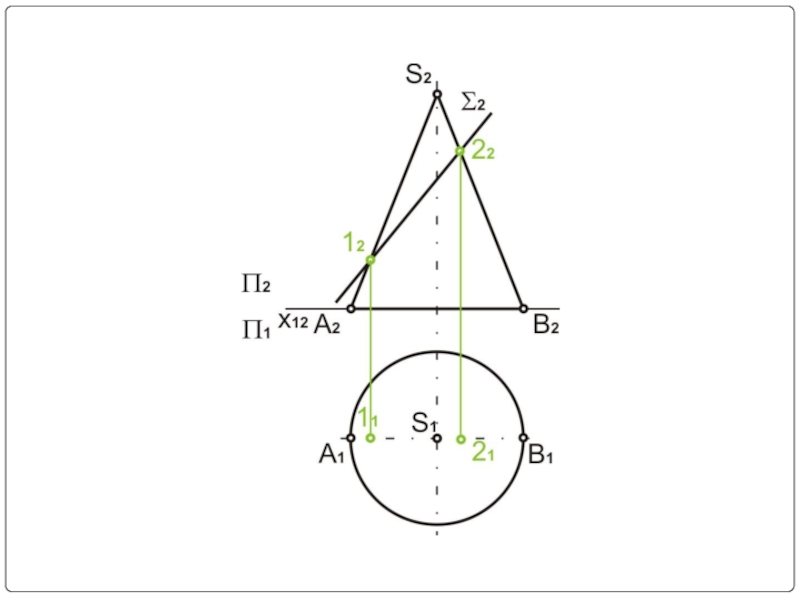
- 14. Фронтально-проецирующая плоскость
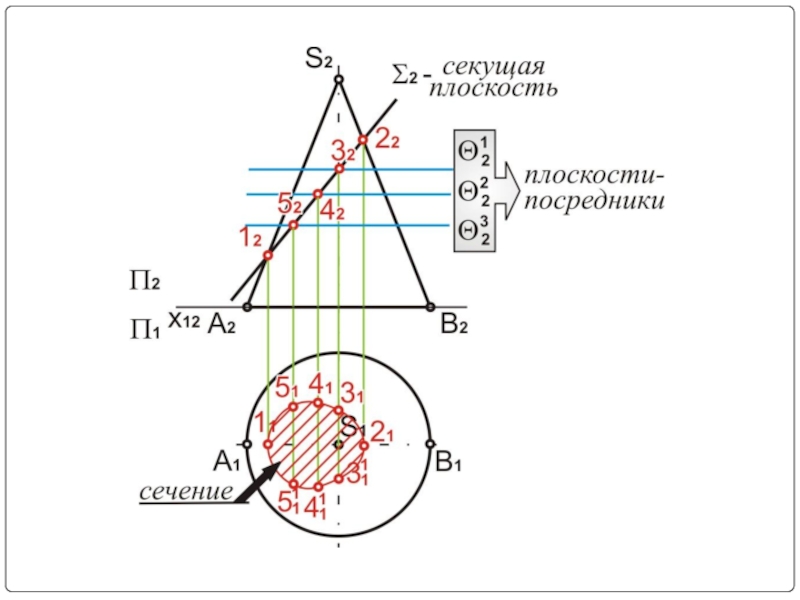
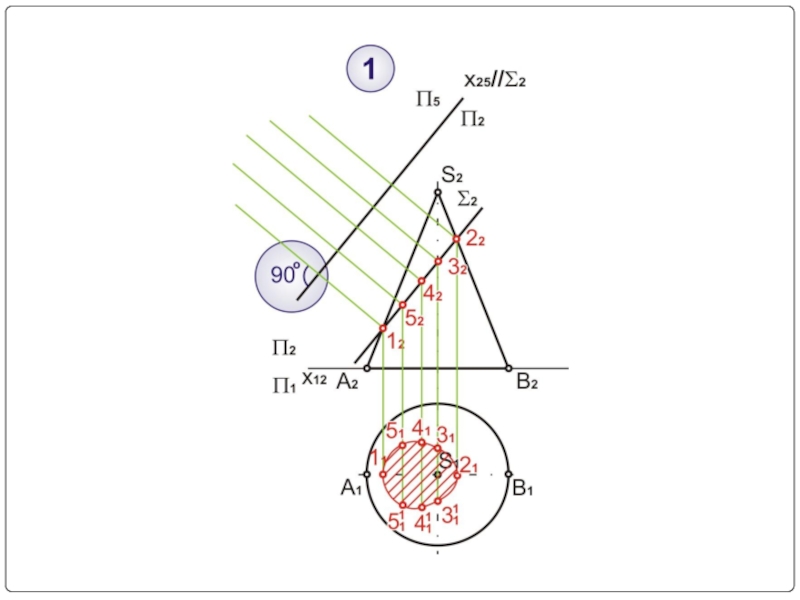
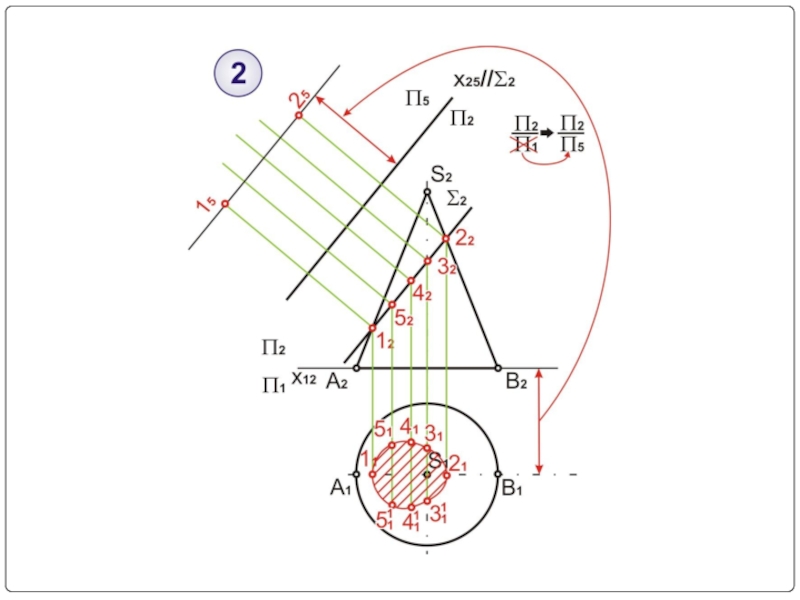
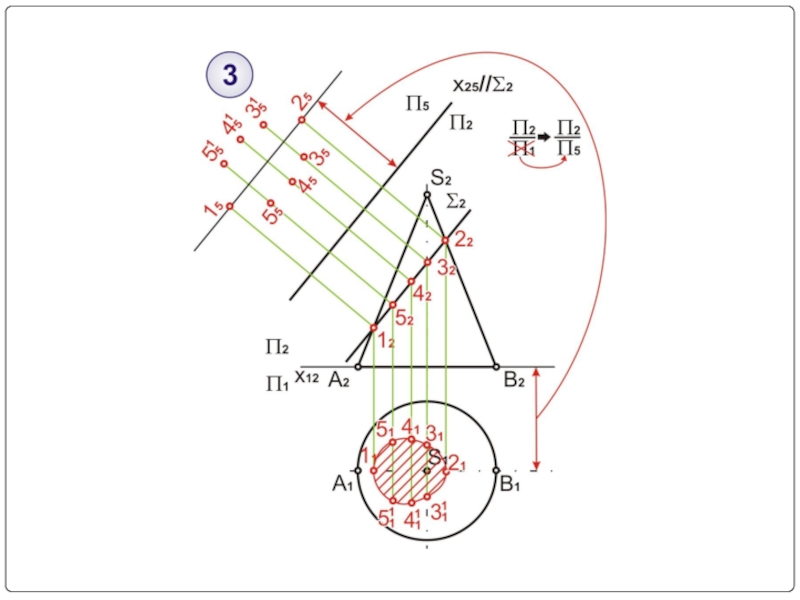
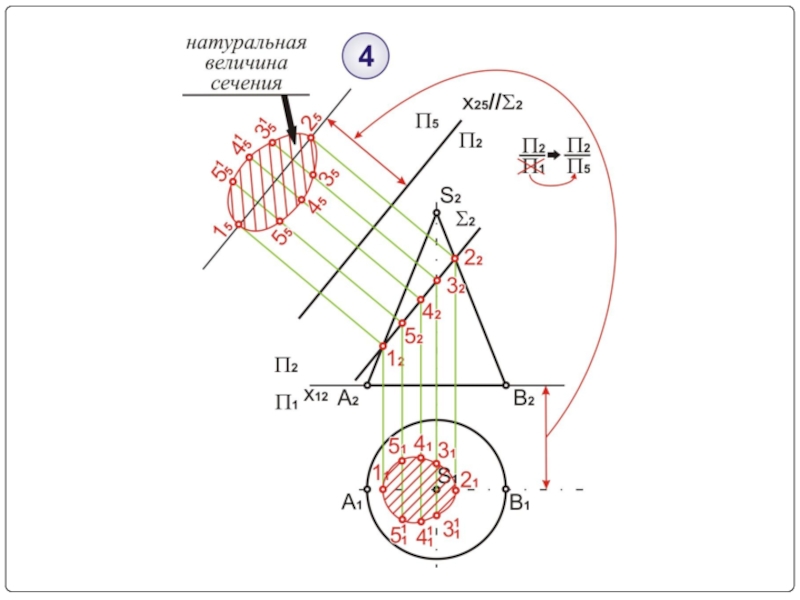
- 15. Пример № 1
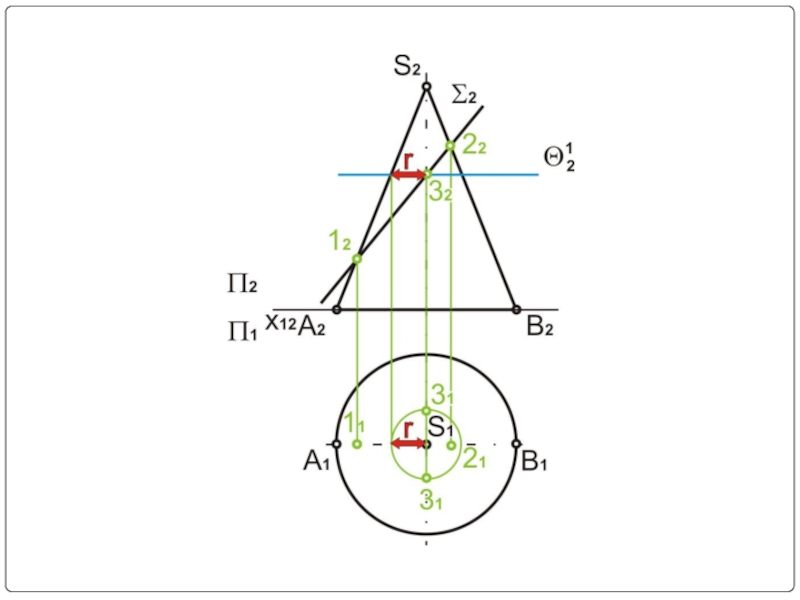
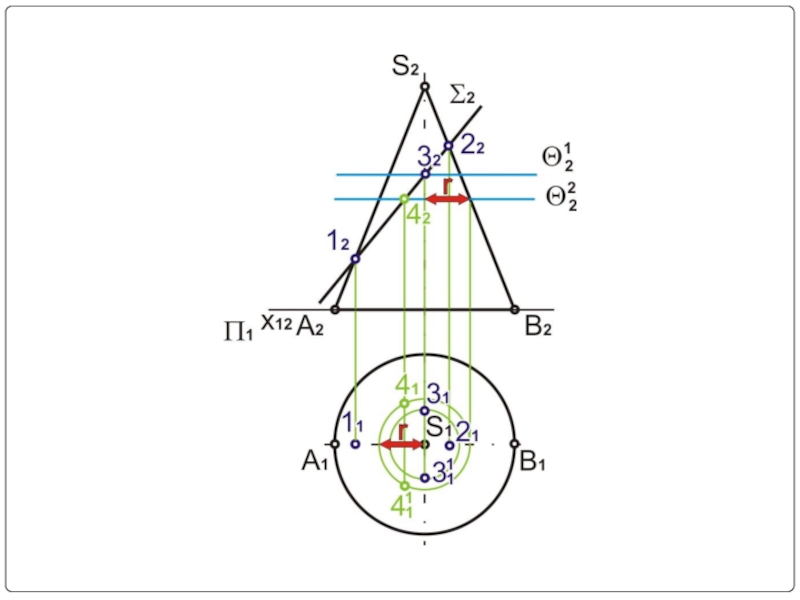
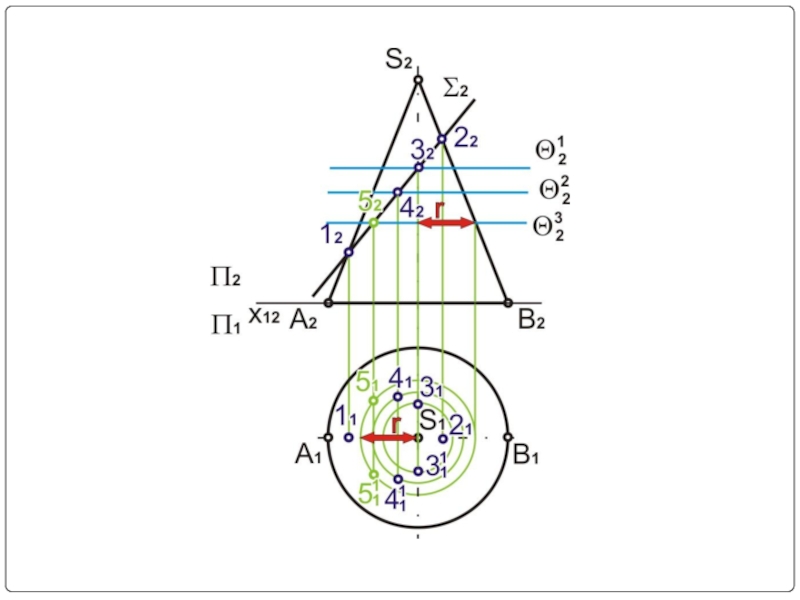
- 16. Σ2 – секущая плоскость (фронтально-проецирующая) Σ2⊥П2
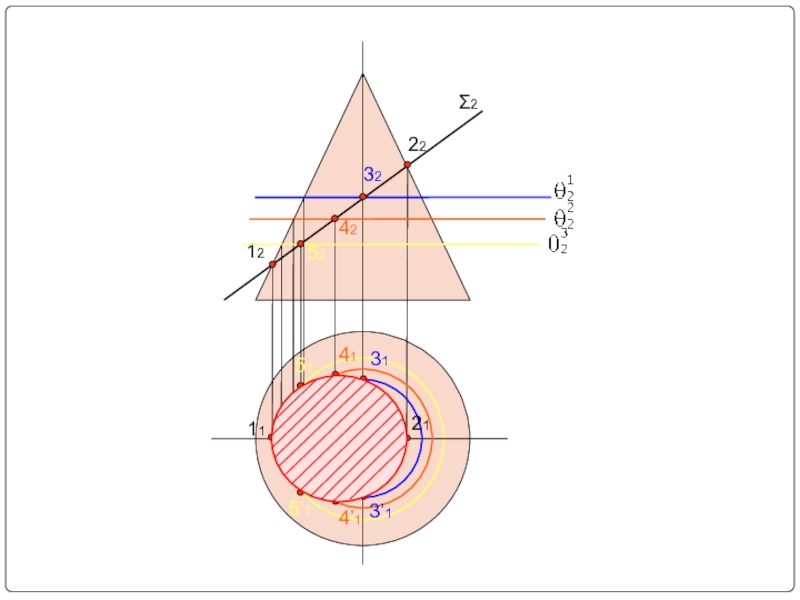
- 26. Пример № 2
- 27. Σ2 22
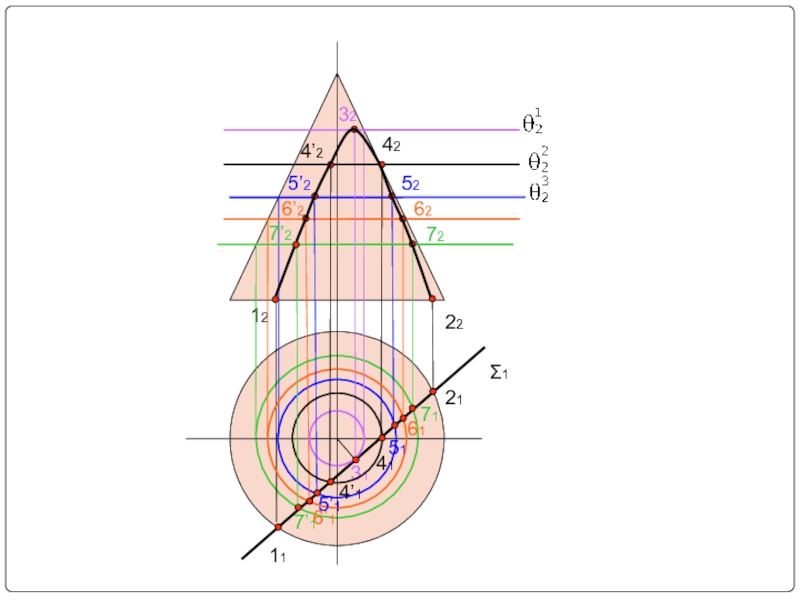
- 28. Горизонтально-проецирующая плоскость
- 29. Σ1 42 12
- 30. Ли В.Г., Калашникова Т.Г. Начертательная геометрия: Рабочая
- 31. Благодарю за внимание http://incampus.ru/campus.aspx?id=9768998
Слайд 1Основные понятия и определения
Поверхности вращения
Таганрог 2014
Инженерно-технологическая академия
Южного федерального университета
Слайд 2http://incampus.ru/campus.aspx?id=9768998
http://egf.tti.sfedu.ru/departments/graphics/staff/staff_56.html
Калашникова Татьяна Григорьевна
к.т.н., доцент кафедры ИГиКД ИТА ЮФУ,
член-корр. Академии информатизации образования
Слайд 4Криволинейные поверхности вращения могут быть образованы при вращении любой кривой линии
Точки образующей линии описывают вокруг оси окружности – параллели (b).
Меридианы (a) - кривые, полученные в результате пересечения поверхности вращения плоскостями, проходящими через ось.
Фронтальный меридиан называют главным.
Параллели и меридианы образуют на поверхности вращения ортогональную сеть (сетчатый каркас поверхности).
Слайд 5Из множества параллелей
поверхности вращения выделяют
параллели, в точках
касательные (t) к меридианам этой
поверхности вращения параллельны
оси вращения:
горловина bmin(t//i);
экватор bmax(t//i).
Слайд 6Основные свойства поверхности вращения:
Любая меридиональная плоскость является ее плоскостью симметрии.
Любое плоское
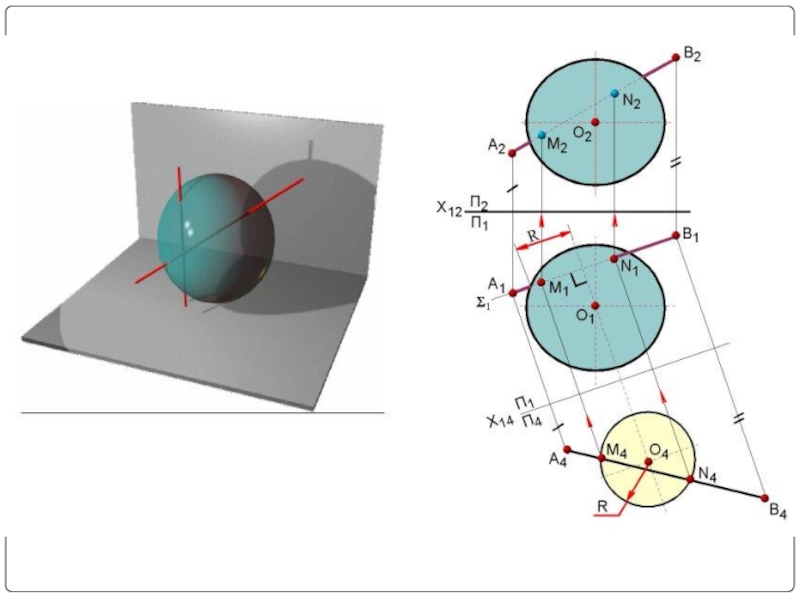
Если поверхности вращения с общей осью вращения пересекаются, то они пересекаются по их общим параллелям.
Слайд 10Рассмотрим построение фигуры конического сечения и определение ее натуральной величины на
Слайд 30Ли В.Г., Калашникова Т.Г. Начертательная геометрия: Рабочая тетрадь для практических занятий
Иллюстрации: Калашникова Т.Г., Ли В.Г.
Рекомендуемая литература:
Материалы дисциплины опубликованы на Цифровом кампусе ТТИ ЮФУ http://incampus.ru/campus.aspx?id=9768998
Вареца В.П. Проекционное моделирование в инженерной графике: Учебное пособие. Таганрог: Изд-во ТРТУ, 2001.
Научно-техническая библиотека ТТИ ЮФУ http://ntb.tsure.ru:
Королев Ю. И. Начертательная геометрия: учебник для студ. вузов. - 2-е изд., перераб. и доп. - М.: Архитектура-С, 2007. - 422 с. : ил. - (Специальность "Архитектура").
Фролов С. А. Начертательная геометрия: учебник для студ. вузов. - 3-е изд., перераб. и доп. - М.: ИНФРА-М, 2008. - 285 с.
Талалай П. Г. Начертательная геометрия. Инженерная графика: Интернет-тестирование базовых знаний : учеб. пособие. - СПб. : Лань, 2010. - 254 с.
Источники: