- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы построения разверток гранных поверхностей презентация
Содержание
- 1. Способы построения разверток гранных поверхностей
- 2. Построение разверток многогранных поверхностей. Поверхности, которые можно
- 3. Построение разверток пирамидальных поверхностей: Боковыми гранями
- 4. Рассмотрим алгоритм построения развертки треугольной пирамиды.
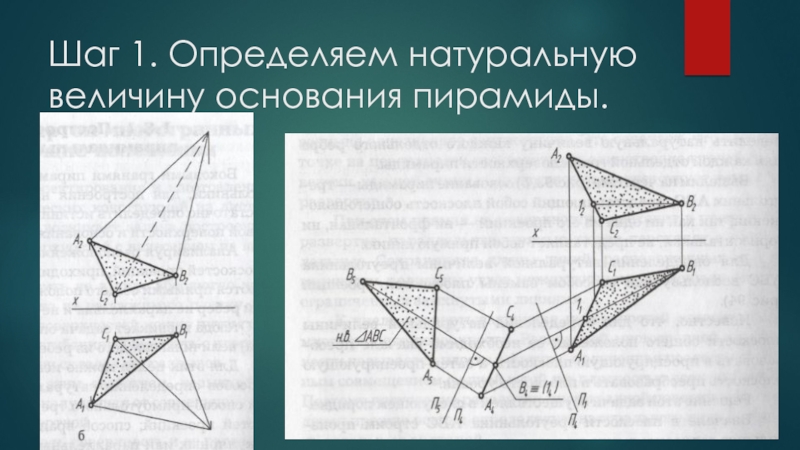
- 5. Шаг 1. Определяем натуральную величину основания пирамиды.
- 6. Шаг 2.Определяем натуральную величину ребер боковой поверхности этой пирамиды.
- 7. Определение натуральной длины ребер способом прямоугольного треугольника.
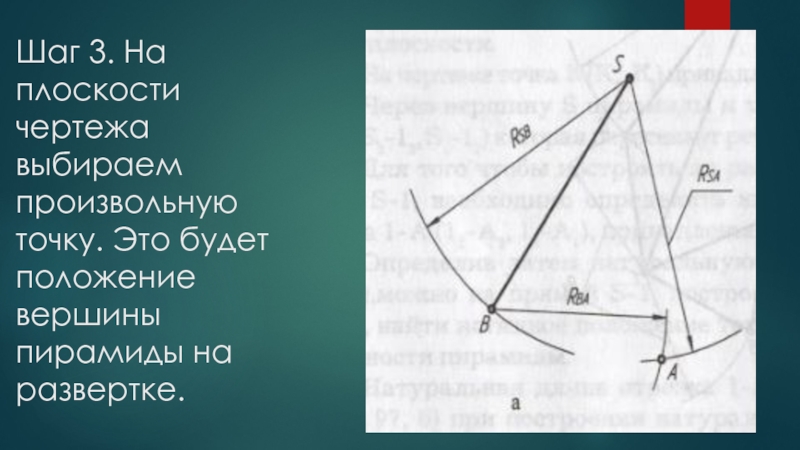
- 8. Шаг 3. На плоскости чертежа выбираем произвольную точку. Это будет положение вершины пирамиды на развертке.
- 9. Шаг 4. От этой точки строим одну
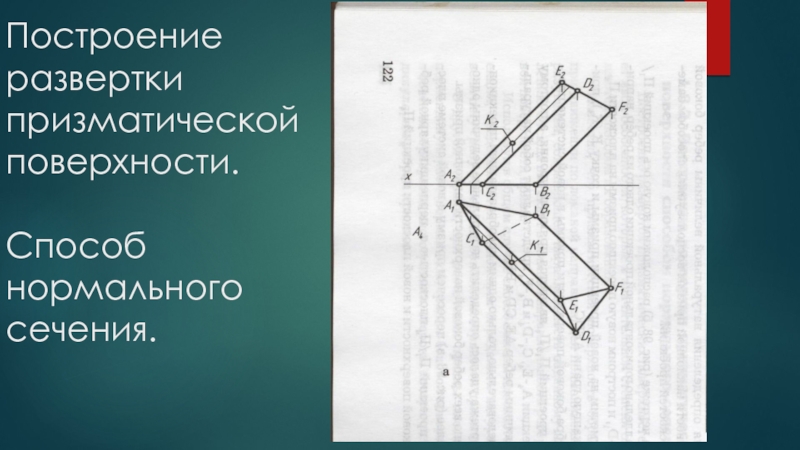
- 10. Построение развертки призматической поверхности. Способ нормального сечения.
- 11. Шаг 1.Воспользовавшись методом замены плоскостей расположим новую
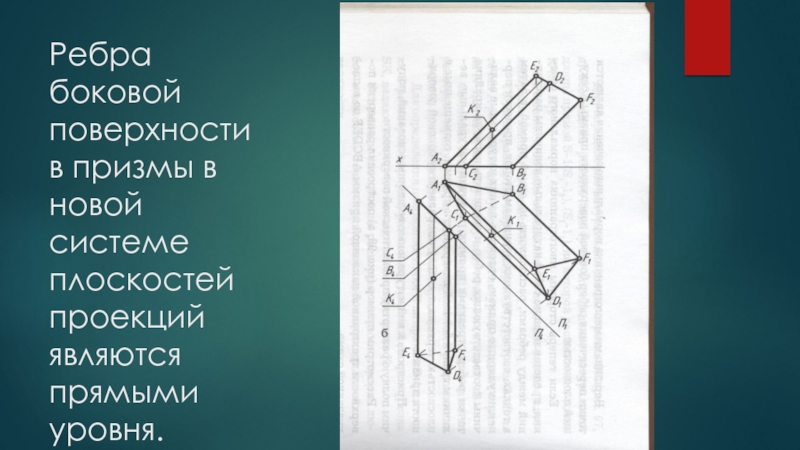
- 12. Ребра боковой поверхности в призмы в новой системе плоскостей проекций являются прямыми уровня.
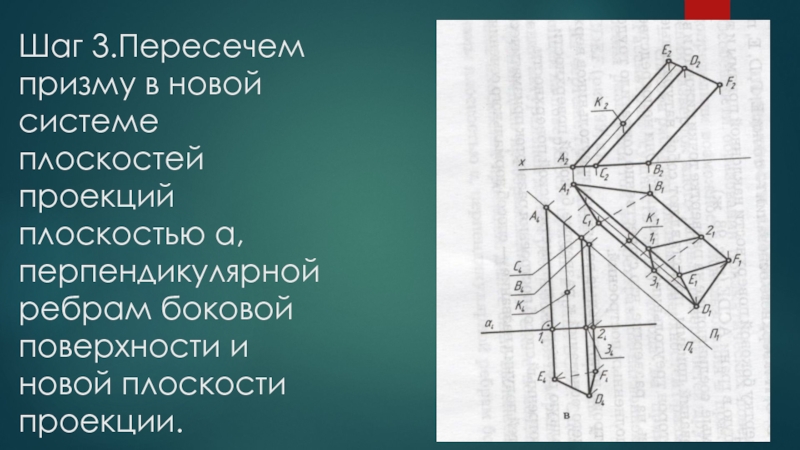
- 13. Шаг 3.Пересечем призму в новой системе плоскостей
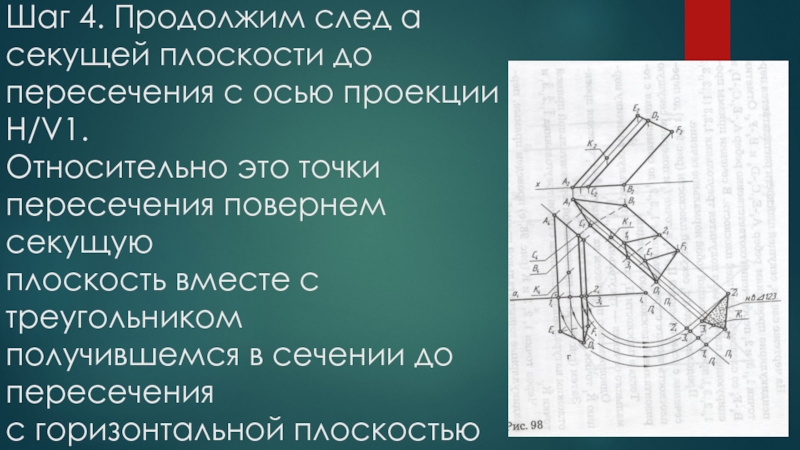
- 14. Шаг 4. Продолжим след α секущей плоскости
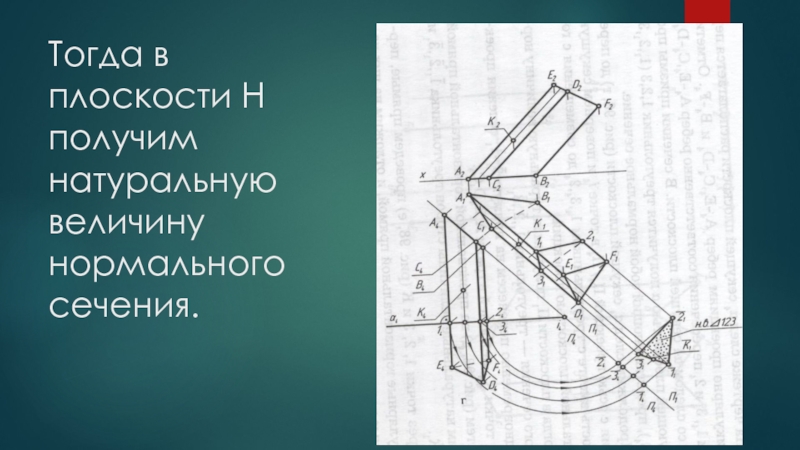
- 15. Тогда в плоскости H получим натуральную величину нормального сечения.
- 16. Шаг 5. На произвольной горизонтальной прямой отложим натуральные величины сторон треугольника, полученного в предыдущем шаге.
- 17. Через точки сторон(1,2,3) проведем прямые перпендикулярные горизонтальной
- 19. Соединяем попарно точки вершин верхнего и нижнего
- 20. Способ раскатки. Особенности образования призматических поверхностей определили
- 21. Шаг 1 Определим натуральную длину ребер с
- 22. Шаг 2 Продолжим след α4 секущей плоскостью
- 23. Шаг 3 Поворачиваем грань С4А4E4D4 вокруг ребра
- 24. Шаг 4 Аналогично поворачиваем до совмещения с
- 25. Шаг 5 Вокруг ребра B4F4 поворачиваем до
- 26. Шаг 6 Получаем полную развертку трехгранной наклонной
Построение разверток многогранных поверхностей. Поверхности, которые можно путем постепенного деформирования(разгибания) совместить с плоскостью так, что при этом не будет ни складок, ни разрывов ,называются развертывающимися, а фигура, полученная от совмещения поверхности
Слайд 2Построение разверток многогранных поверхностей.
Поверхности, которые можно путем постепенного деформирования(разгибания) совместить с
плоскостью так, что при этом не будет ни складок, ни разрывов ,называются развертывающимися, а фигура, полученная от совмещения поверхности с плоскостью – разверткой.
К числу развертывающихся поверхностей относятся все многогранные поверхности.
К числу развертывающихся поверхностей относятся все многогранные поверхности.
Слайд 3Построение разверток пирамидальных поверхностей:
Боковыми гранями пирамиды являются треугольники, для построения натуральной
величины которых достаточно определить истинные длины их сторон-ребер боковой поверхности и основания пирамиды.
Для этих целей можно использовать любой из известных способов определения натуральной длины прямой.
Для этих целей можно использовать любой из известных способов определения натуральной длины прямой.
Слайд 8Шаг 3. На плоскости чертежа выбираем произвольную точку. Это будет положение
вершины пирамиды на развертке.
Слайд 9Шаг 4. От этой точки строим одну из боковых граней и
относительно ее достраиваем все остальные.
Слайд 11Шаг 1.Воспользовавшись методом замены плоскостей расположим новую ось проекций параллельно горизонтальной
проекции одного из ребер и построим новую проекцию призмы на плоскость V1.
Слайд 12Ребра боковой поверхности в призмы в новой системе плоскостей проекций являются
прямыми уровня.
Слайд 13Шаг 3.Пересечем призму в новой системе плоскостей проекций плоскостью α, перпендикулярной
ребрам боковой поверхности и новой плоскости проекции.
Слайд 14Шаг 4. Продолжим след α секущей плоскости до пересечения с осью
проекции H/V1.
Относительно это точки
пересечения повернем секущую
плоскость вместе с
треугольником
получившемся в сечении до пересечения
с горизонтальной плоскостью проекции.
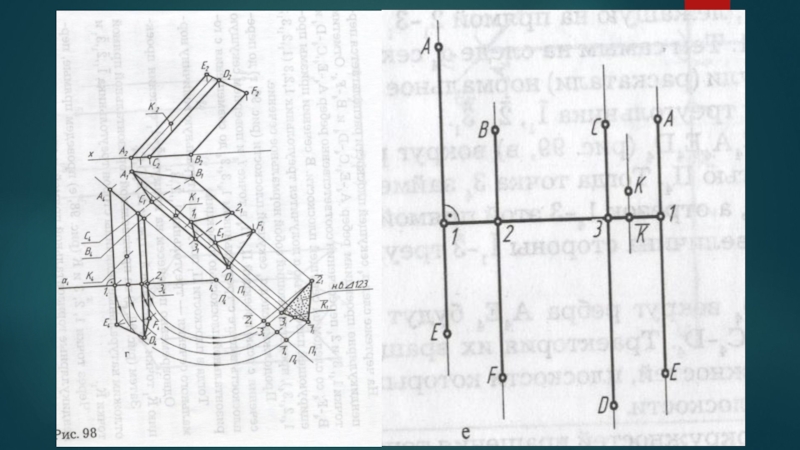
Слайд 16Шаг 5. На произвольной горизонтальной прямой отложим натуральные величины сторон треугольника,
полученного в предыдущем шаге.
Слайд 17Через точки сторон(1,2,3) проведем прямые перпендикулярные горизонтальной прямой, и отложим на
них натуральные величины расстояний от вершин А4,С4,В4,Е4,F4,D4 до следа α секущей плоскости.
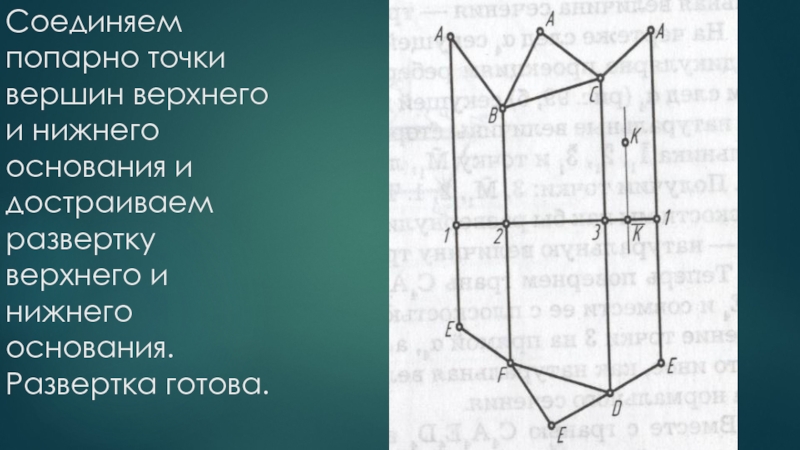
Слайд 19Соединяем попарно точки вершин верхнего и нижнего основания и достраиваем развертку
верхнего и нижнего основания.
Развертка готова.
Слайд 20Способ раскатки.
Особенности образования призматических поверхностей определили возможность использования в практике построения
разверток многогранных поверхностей другого способа – способа раскатки боковых поверхностей призм.
Рассмотрим сущность этого метода на примере построения развертки той же трехгранной наклонной призмы ABCDEF.
Рассмотрим сущность этого метода на примере построения развертки той же трехгранной наклонной призмы ABCDEF.
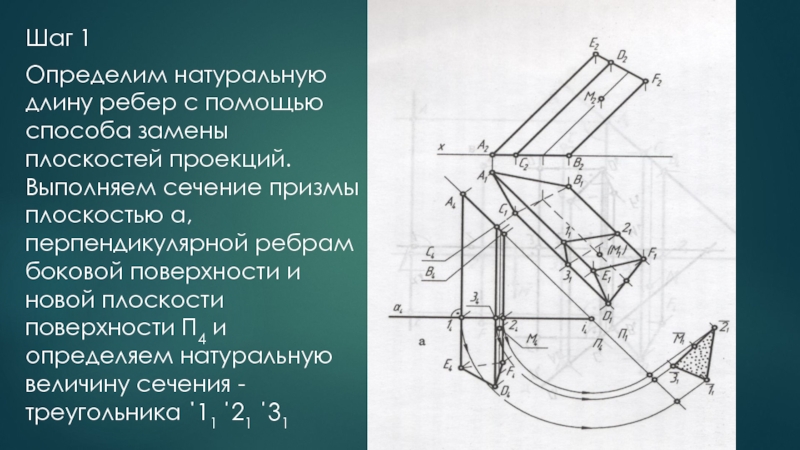
Слайд 21Шаг 1
Определим натуральную длину ребер с помощью способа замены плоскостей проекций.
Выполняем
сечение призмы плоскостью α, перпендикулярной ребрам боковой поверхности и новой плоскости поверхности П4 и определяем натуральную величину сечения - треугольника ΄11 ΄21 ΄31
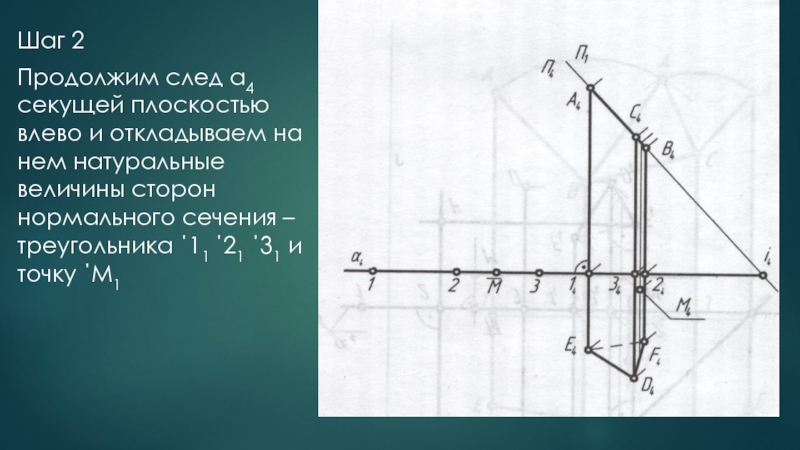
Слайд 22Шаг 2
Продолжим след α4 секущей плоскостью влево и откладываем на нем
натуральные величины сторон нормального сечения – треугольника ΄11 ΄21 ΄31 и точку ΄М1
Слайд 23Шаг 3
Поворачиваем грань С4А4E4D4 вокруг ребра A4E4 и совмещаем ее с
плоскостью П4 .
Через точку 3 на следе α4 проводим прямую, параллельную ребру C4D4. В пересечении этой прямой с проекциями траекторий вращений точек С4 и D4 получаем точки C и D
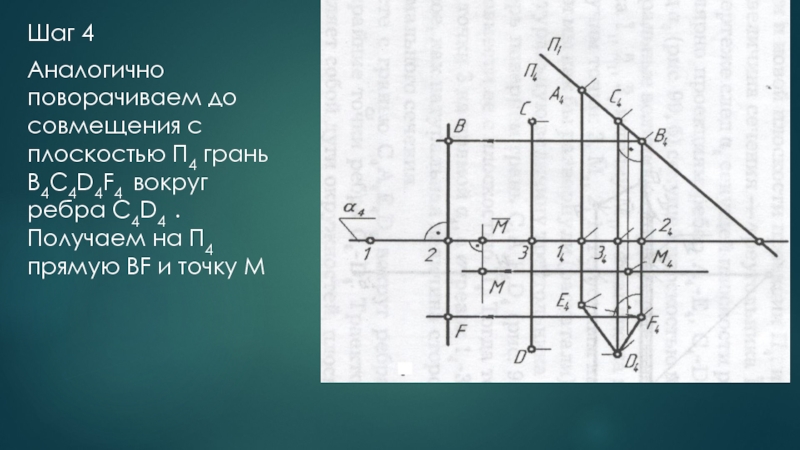
Слайд 24Шаг 4
Аналогично поворачиваем до совмещения с плоскостью П4 грань B4C4D4F4 вокруг
ребра C4D4 .
Получаем на П4 прямую BF и точку M
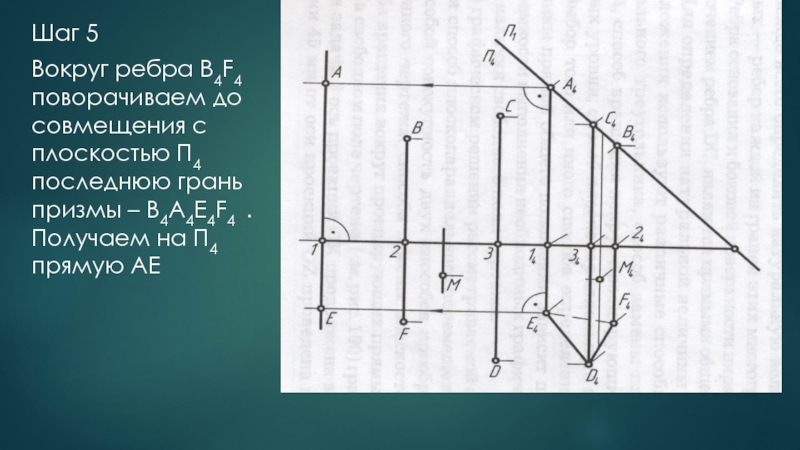
Слайд 25Шаг 5
Вокруг ребра B4F4 поворачиваем до совмещения с плоскостью П4 последнюю
грань призмы – B4A4E4F4 .
Получаем на П4 прямую АЕ
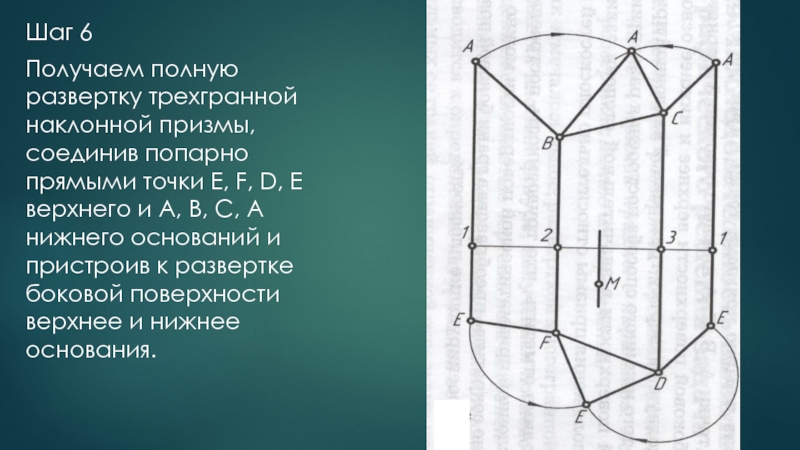
Слайд 26Шаг 6
Получаем полную развертку трехгранной наклонной призмы, соединив попарно прямыми точки
E, F, D, E верхнего и A, B, C, A нижнего оснований и пристроив к развертке боковой поверхности верхнее и нижнее основания.
