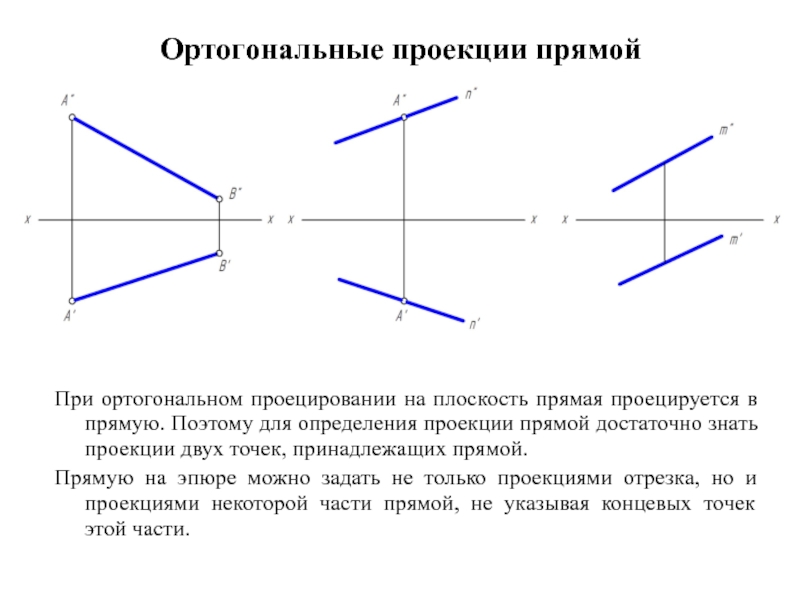
Поэтому для определения проекции прямой достаточно знать проекции двух точек, принадлежащих прямой.
Прямую на эпюре можно задать не только проекциями отрезка, но и проекциями некоторой части прямой, не указывая концевых точек этой части.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ортогональные проекции прямой презентация
Содержание
- 1. Ортогональные проекции прямой
- 2. Прямая общего положения Прямая общего положения –
- 3. Следы прямой Прямая общего положения пересекает все
- 4. Следы прямой Перейдя от пространственной картины к
- 5. Следы прямой Проведя линию связи из полученной
- 6. Следы прямой Для нахождения фронтального следа прямой
- 7. Следы прямой Проведя линию связи из полученной
- 8. Частные случаи расположения прямой Кроме
- 9. Прямые, параллельные плоскости проекции – линии уровня
- 10. Прямые, параллельные плоскости проекции – линии уровня
- 11. Прямые, параллельные плоскости проекции – линии уровня
- 12. Прямые, перпендикулярные плоскости проекции – проецирующие прямые
- 13. Прямые, перпендикулярные плоскости проекции – проецирующие прямые
- 14. Прямые, перпендикулярные плоскости проекции – проецирующие прямые
- 15. Определение натуральной величины отрезка общего положения Ортогональная
- 16. Спроецируем отрезок общего положения АВ на
- 17. АВ является гипотенузой прямоугольного треугольника, у
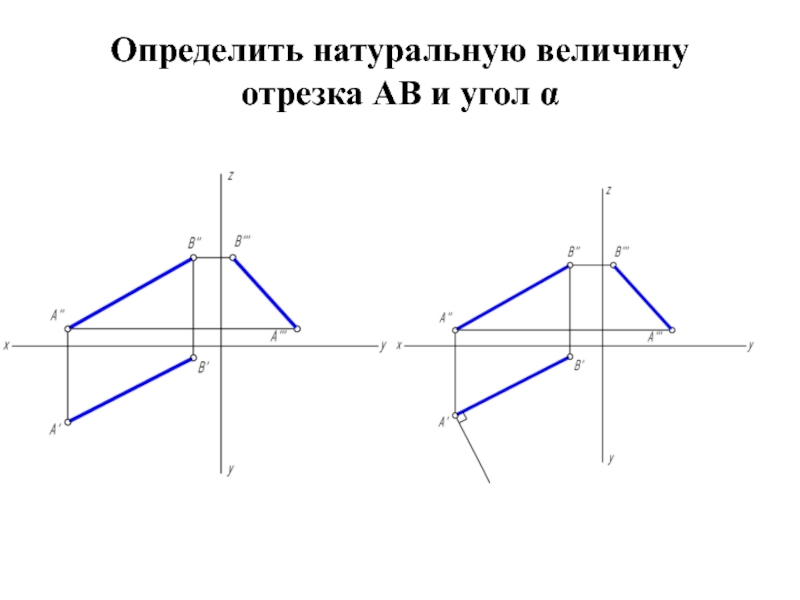
- 18. Определить натуральную величину отрезка АВ и угол α
- 20. Взаимное положение прямых Прямые в пространстве могут
- 21. Параллельные прямые Правило для построения на эпюре
- 22. Причем, если в пространстве прямые a
- 23. Определить параллельны ли заданные отрезки
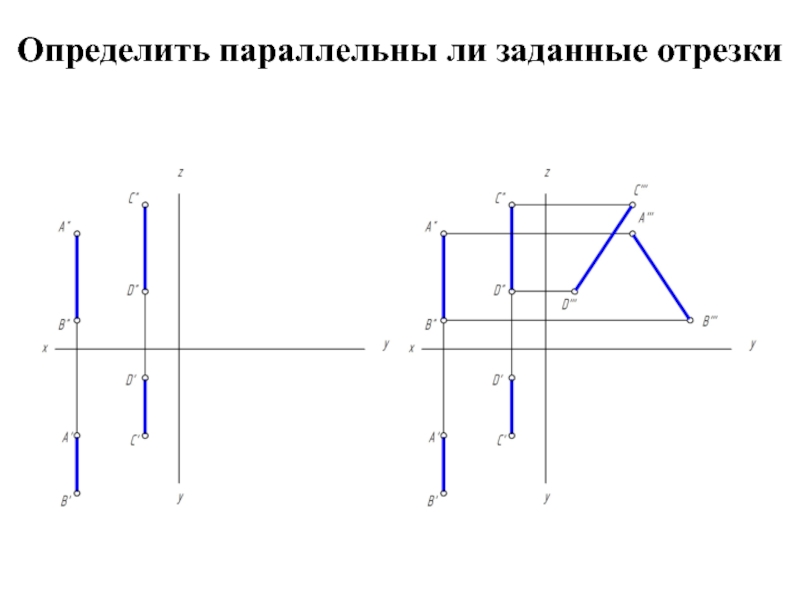
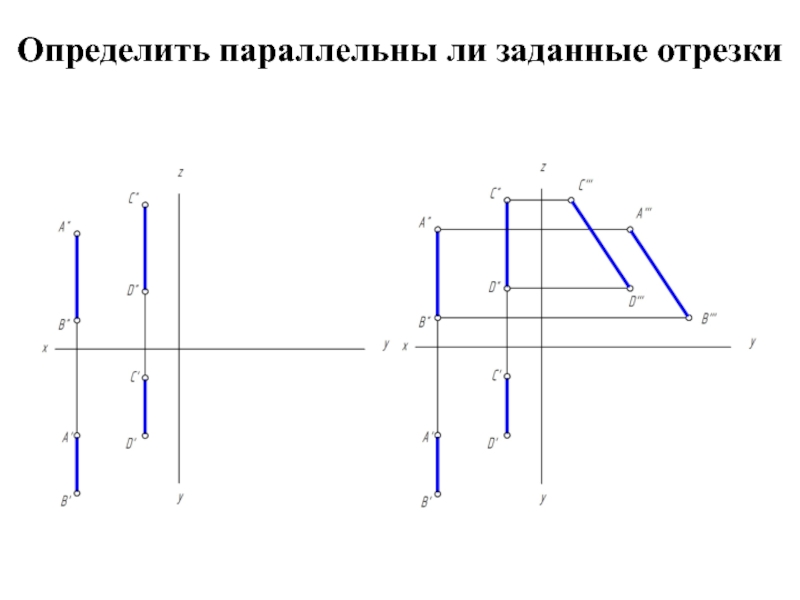
- 24. Определить параллельны ли заданные отрезки
- 25. Пересекающиеся прямые Точка пересечения проекций пересекающихся прямых
- 26. Достроить фронтальную проекцию отрезка CD, пересекающего отрезок
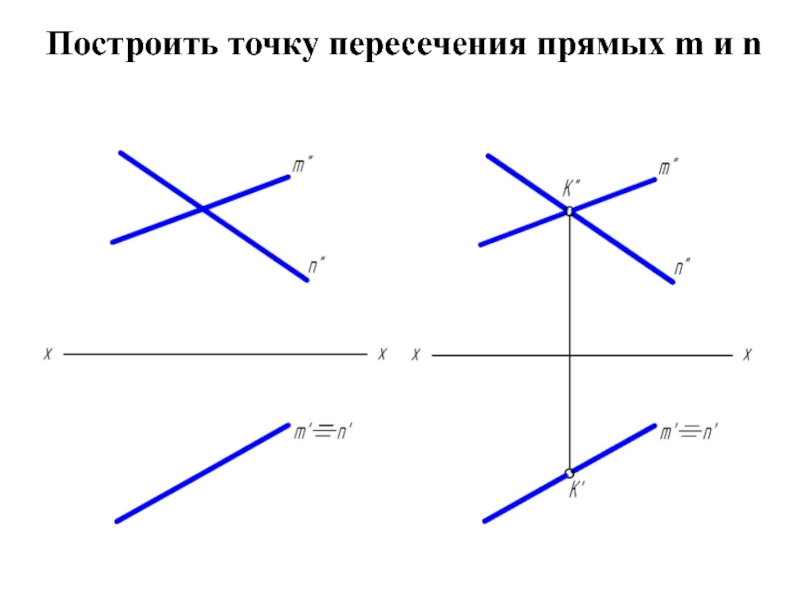
- 27. Построить точку пересечения прямых m и n
- 28. Для прямых общего положения необходимым и
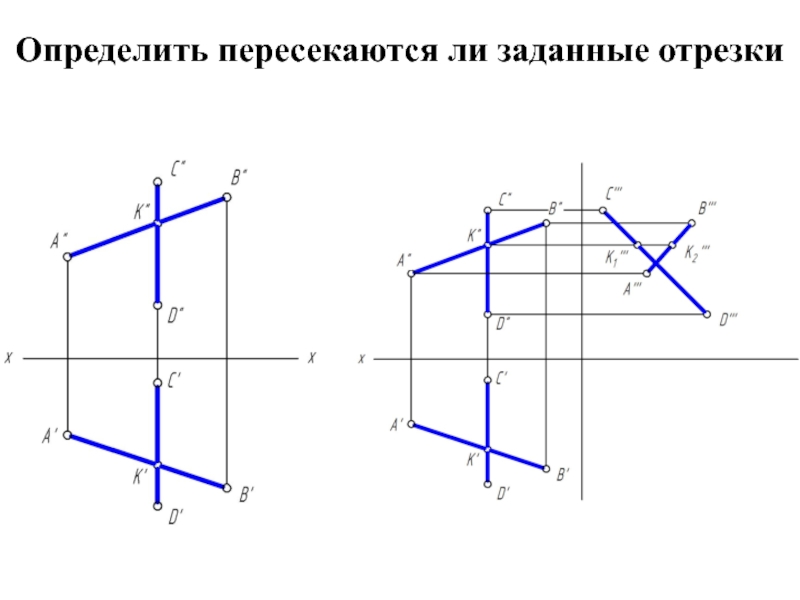
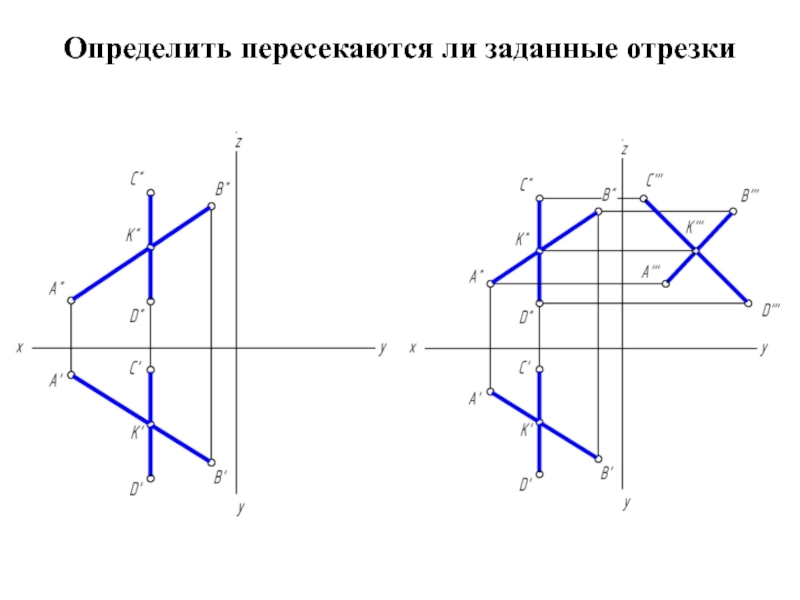
- 29. Определить пересекаются ли заданные отрезки
- 30. Определить пересекаются ли заданные отрезки
- 31. Скрещивающиеся прямые Скрещивающиеся прямые не пересекаются и
- 32. Точка пересечения одноименных проекций представляет собой
- 33. Свойства проекций плоских углов 1. Если стороны
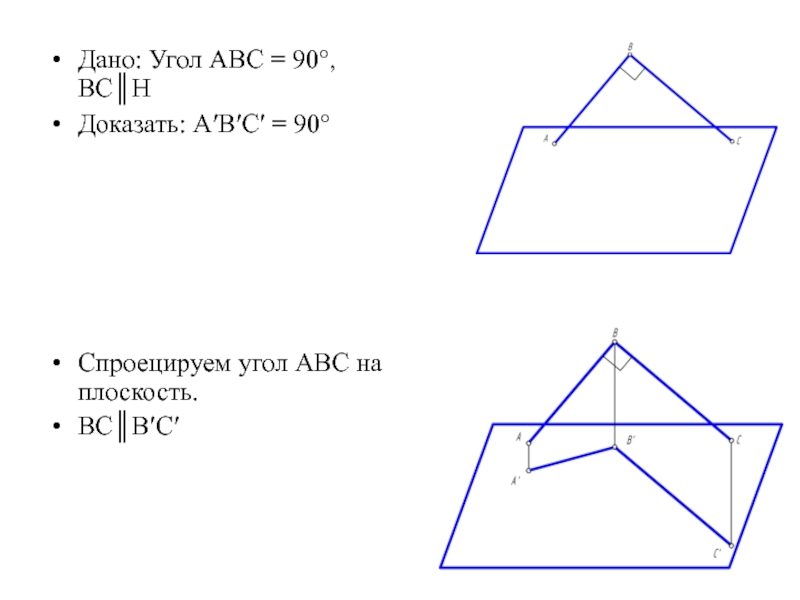
- 34. Дано: Угол АВС = 90°, ВС║Н
- 35. Продолжим АВ до пересечения с Н
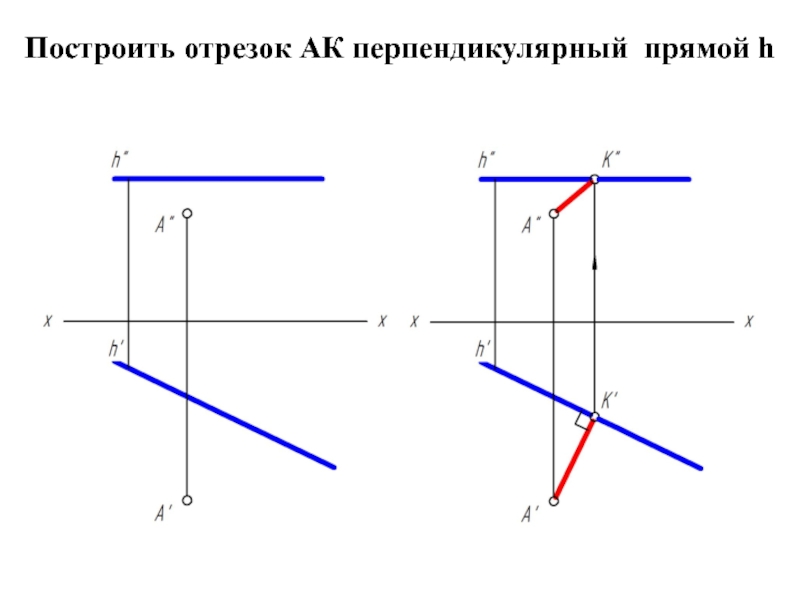
- 36. Построить отрезок АК перпендикулярный прямой h
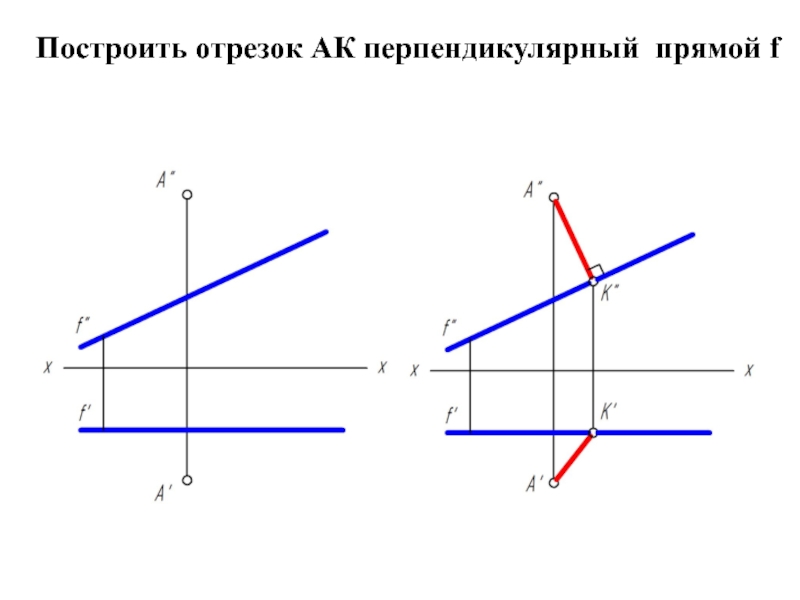
- 37. Построить отрезок АК перпендикулярный прямой f
Слайд 1Ортогональные проекции прямой
При ортогональном проецировании на плоскость прямая проецируется в прямую.
Слайд 2Прямая общего положения
Прямая общего положения – это прямая, занимающая произвольное положение
по отношению к плоскостям проекций, при этом углы наклона к плоскостям H, V и W отличны от 0° и 90°.
На эпюре проекции прямой общего положения составляют с осями координат также произвольные углы.
Углы между проекциями прямой общего положения и осями не равны углам наклона прямой к плоскостям проекций.
На эпюре проекции прямой общего положения составляют с осями координат также произвольные углы.
Углы между проекциями прямой общего положения и осями не равны углам наклона прямой к плоскостям проекций.
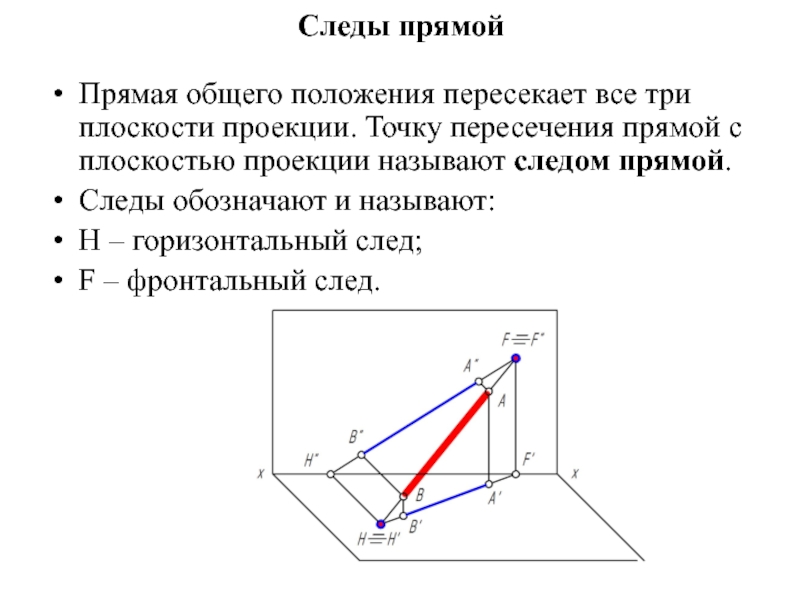
Слайд 3Следы прямой
Прямая общего положения пересекает все три плоскости проекции. Точку пересечения
прямой с плоскостью проекции называют следом прямой.
Следы обозначают и называют:
H – горизонтальный след;
F – фронтальный след.
Следы обозначают и называют:
H – горизонтальный след;
F – фронтальный след.
Слайд 4Следы прямой
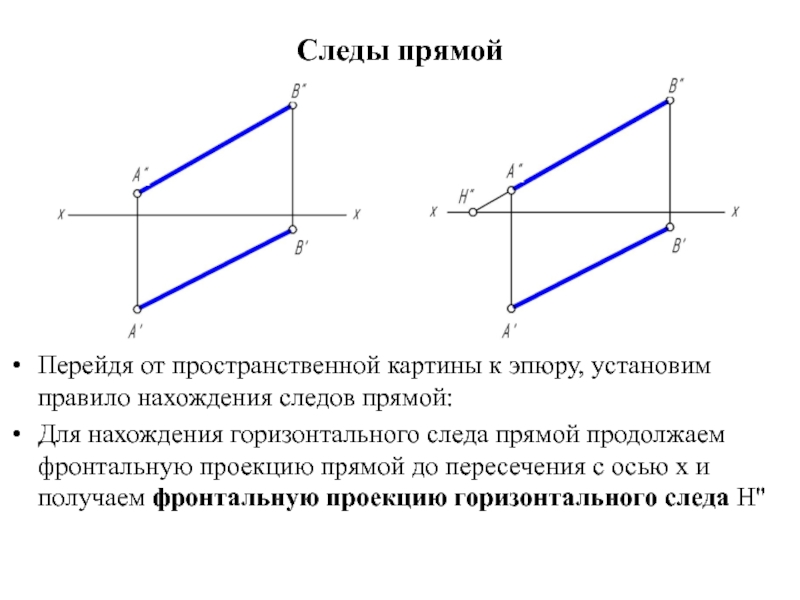
Перейдя от пространственной картины к эпюру, установим правило нахождения следов
прямой:
Для нахождения горизонтального следа прямой продолжаем фронтальную проекцию прямой до пересечения с осью х и получаем фронтальную проекцию горизонтального следа H''
Для нахождения горизонтального следа прямой продолжаем фронтальную проекцию прямой до пересечения с осью х и получаем фронтальную проекцию горизонтального следа H''
Слайд 5Следы прямой
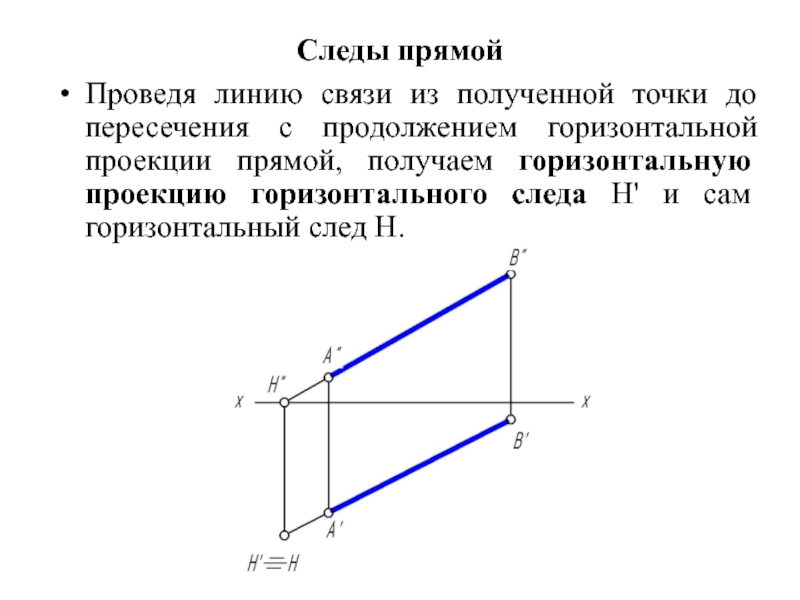
Проведя линию связи из полученной точки до пересечения с продолжением
горизонтальной проекции прямой, получаем горизонтальную проекцию горизонтального следа H' и сам горизонтальный след H.
Слайд 6Следы прямой
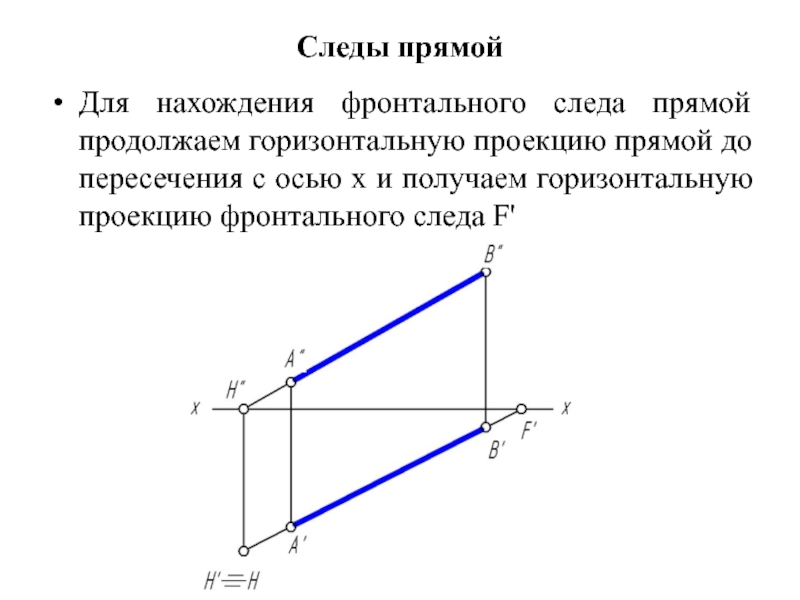
Для нахождения фронтального следа прямой продолжаем горизонтальную проекцию прямой до
пересечения с осью х и получаем горизонтальную проекцию фронтального следа F'
Слайд 7Следы прямой
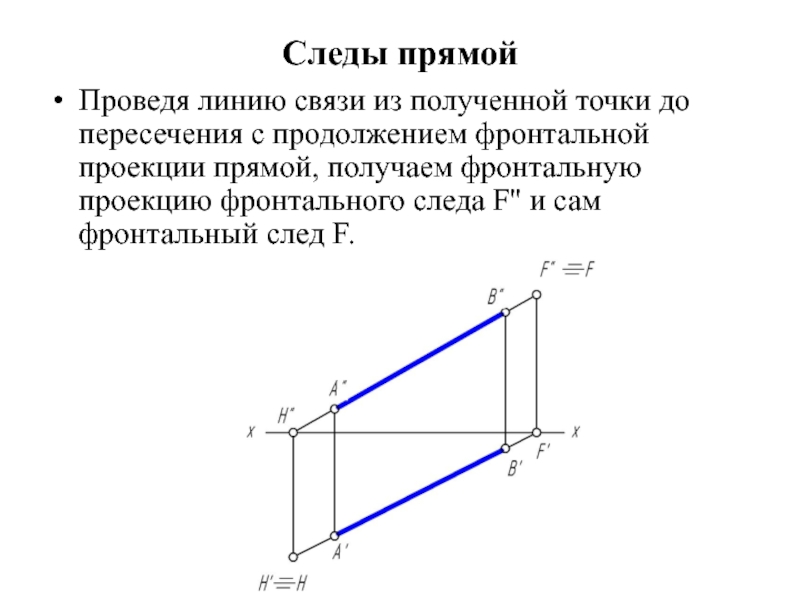
Проведя линию связи из полученной точки до пересечения с продолжением
фронтальной проекции прямой, получаем фронтальную проекцию фронтального следа F'' и сам фронтальный след F.
Слайд 8Частные случаи расположения прямой
Кроме рассмотренного общего случая, прямая по
отношению к заданной системе плоскостей проекций может занимать частное положение:
а) параллельное плоскости проекции;
б) перпендикулярное плоскости проекции;
в) принадлежать плоскости проекции.
а) параллельное плоскости проекции;
б) перпендикулярное плоскости проекции;
в) принадлежать плоскости проекции.
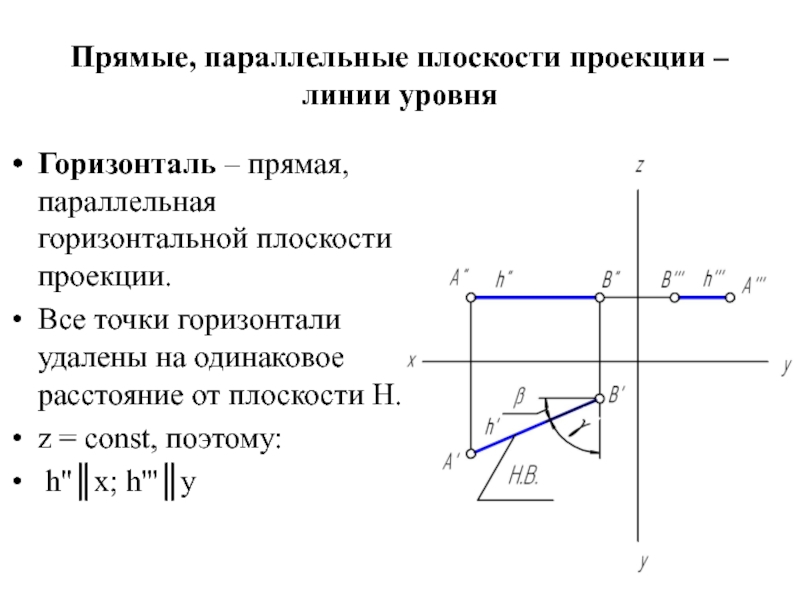
Слайд 9Прямые, параллельные плоскости проекции – линии уровня
Горизонталь – прямая, параллельная горизонтальной
плоскости проекции.
Все точки горизонтали удалены на одинаковое расстояние от плоскости Н.
z = const, поэтому:
h''║x; h'''║y
Все точки горизонтали удалены на одинаковое расстояние от плоскости Н.
z = const, поэтому:
h''║x; h'''║y
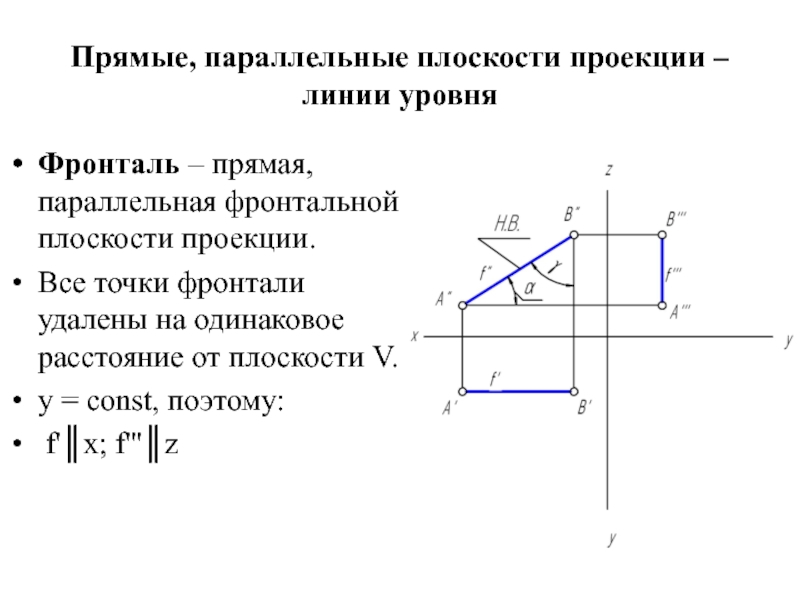
Слайд 10Прямые, параллельные плоскости проекции – линии уровня
Фронталь – прямая, параллельная фронтальной
плоскости проекции.
Все точки фронтали удалены на одинаковое расстояние от плоскости V.
y = const, поэтому:
f'║x; f'''║z
Все точки фронтали удалены на одинаковое расстояние от плоскости V.
y = const, поэтому:
f'║x; f'''║z
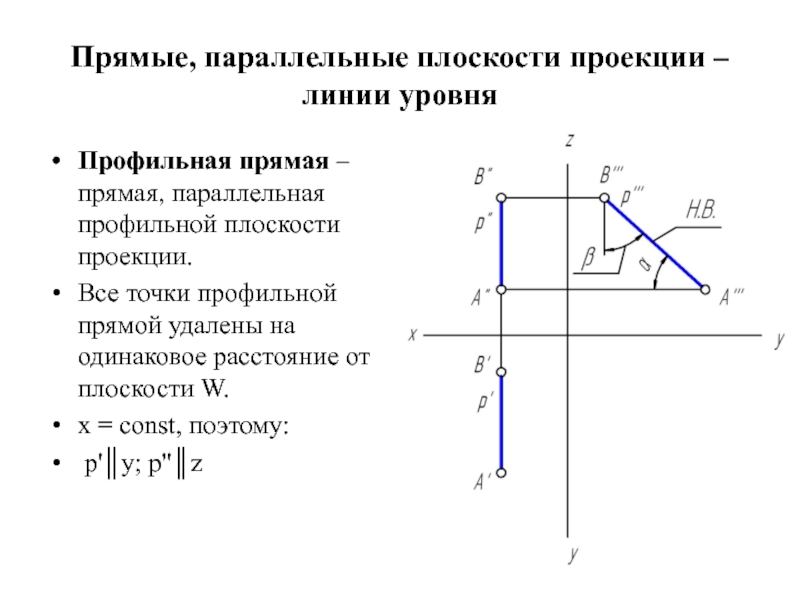
Слайд 11Прямые, параллельные плоскости проекции – линии уровня
Профильная прямая – прямая, параллельная
профильной плоскости проекции.
Все точки профильной прямой удалены на одинаковое расстояние от плоскости W.
x = const, поэтому:
p'║y; p''║z
Все точки профильной прямой удалены на одинаковое расстояние от плоскости W.
x = const, поэтому:
p'║y; p''║z
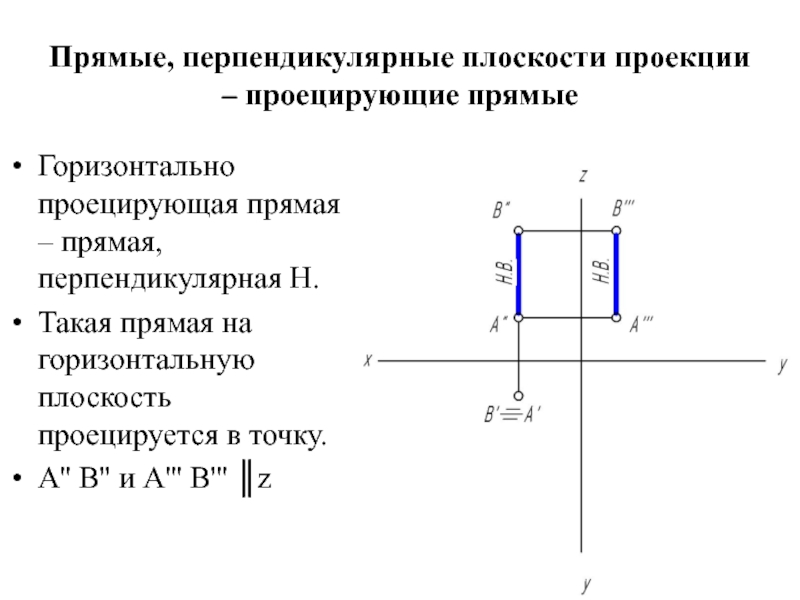
Слайд 12Прямые, перпендикулярные плоскости проекции – проецирующие прямые
Горизонтально проецирующая прямая – прямая,
перпендикулярная Н.
Такая прямая на горизонтальную плоскость проецируется в точку.
А'' В'' и А''' В''' ║z
Такая прямая на горизонтальную плоскость проецируется в точку.
А'' В'' и А''' В''' ║z
Слайд 13Прямые, перпендикулярные плоскости проекции – проецирующие прямые
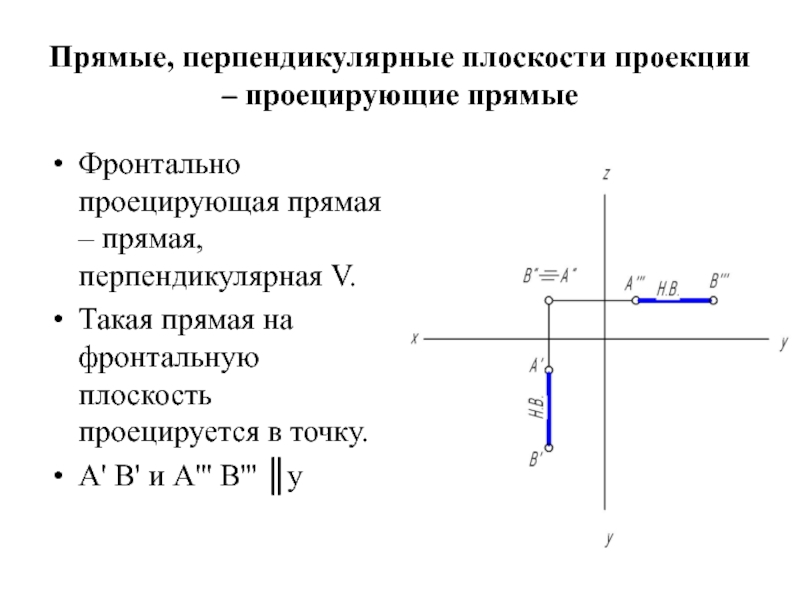
Фронтально проецирующая прямая – прямая,
перпендикулярная V.
Такая прямая на фронтальную плоскость проецируется в точку.
А' В' и А''' В''' ║y
Такая прямая на фронтальную плоскость проецируется в точку.
А' В' и А''' В''' ║y
Слайд 14Прямые, перпендикулярные плоскости проекции – проецирующие прямые
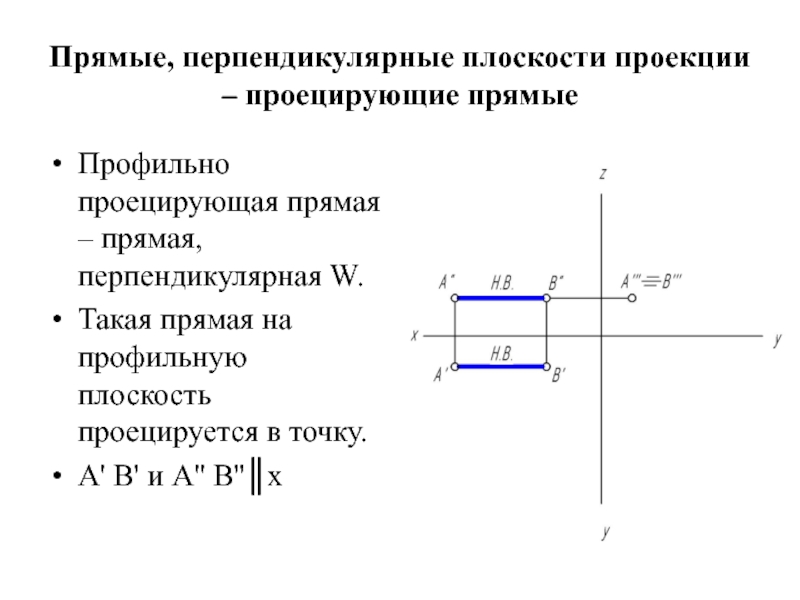
Профильно проецирующая прямая – прямая,
перпендикулярная W.
Такая прямая на профильную плоскость проецируется в точку.
А' В' и А'' В''║x
Такая прямая на профильную плоскость проецируется в точку.
А' В' и А'' В''║x
Слайд 15Определение натуральной величины отрезка общего положения
Ортогональная проекция отрезка на плоскость Н
(V или W) будет конгруэнтна оригиналу лишь в том случае, когда он параллелен плоскости проекции Н (V или W).
Во всех остальных случаях он проецируется на плоскость проекции с искажением. При этом ортогональная проекция отрезка всегда будет меньше его натуральной величины.
Во всех остальных случаях он проецируется на плоскость проекции с искажением. При этом ортогональная проекция отрезка всегда будет меньше его натуральной величины.
Слайд 16
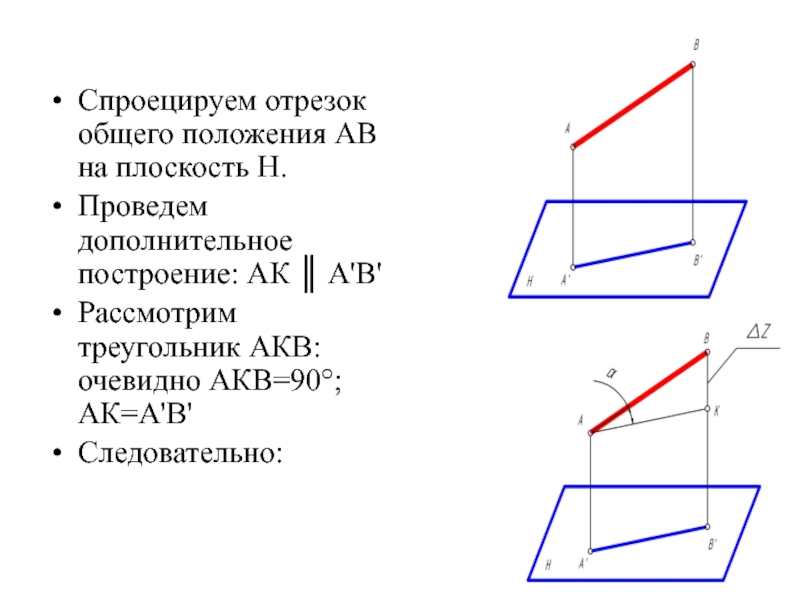
Спроецируем отрезок общего положения АВ на плоскость Н.
Проведем дополнительное построение: АК
║ А'В'
Рассмотрим треугольник АКВ: очевидно АКВ=90°; АК=А'В'
Следовательно:
Рассмотрим треугольник АКВ: очевидно АКВ=90°; АК=А'В'
Следовательно:
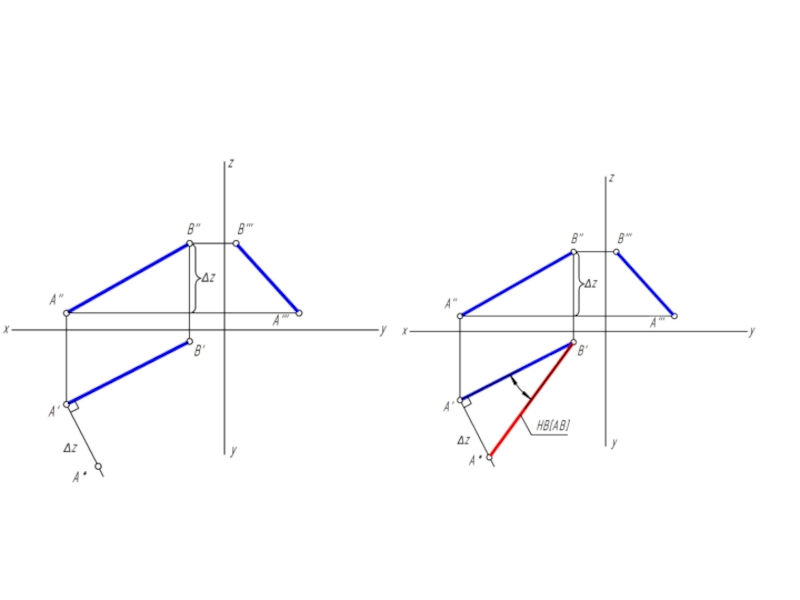
Слайд 17
АВ является гипотенузой прямоугольного треугольника, у которого один катет равен проекции
самого отрезка, а второй катет равен разности расстояний концов отрезка до этой же плоскости проекций.
Угол наклона прямой к плоскости проекций в пространстве на эпюре измерится углом между гипотенузой прямоугольного треугольника и проекцией отрезка на эту же плоскость проекций.
Угол наклона прямой к плоскости проекций в пространстве на эпюре измерится углом между гипотенузой прямоугольного треугольника и проекцией отрезка на эту же плоскость проекций.
Слайд 20Взаимное положение прямых
Прямые в пространстве могут быть:
параллельными;
пересекающимися;
скрещивающимися.
скрещивающимися.
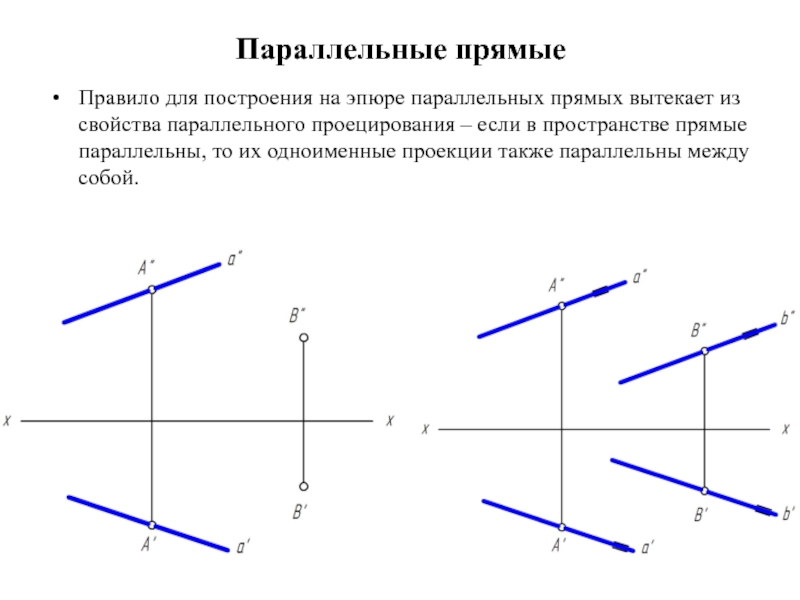
Слайд 21Параллельные прямые
Правило для построения на эпюре параллельных прямых вытекает из свойства
параллельного проецирования – если в пространстве прямые параллельны, то их одноименные проекции также параллельны между собой.
Слайд 22
Причем, если в пространстве прямые a и b занимают общее положение
относительно плоскостей проекций, то для выяснения по эпюру вопроса о параллельности прямых достаточно убедиться, будут ли параллельны между собой их одноименные проекции только на двух плоскостях. Параллельность проекции на третьей плоскости в этом случае автоматически удовлетворяется.
Если прямые параллельны какой-либо плоскости проекции (например W), то для выяснения вопроса будут ли прямые параллельны в пространстве следует убедиться в параллельности их профильных проекций.
Если прямые параллельны какой-либо плоскости проекции (например W), то для выяснения вопроса будут ли прямые параллельны в пространстве следует убедиться в параллельности их профильных проекций.
Слайд 25Пересекающиеся прямые
Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих
прямых (свойство параллельного проецирования).
Слайд 26Достроить фронтальную проекцию отрезка CD, пересекающего отрезок АВ в точке К.
Точка
К принадлежит [АВ]; Точка К принадлежит [CD],
Следовательно: точка К – общая для [АВ] и [CD].
Следовательно: точка К – общая для [АВ] и [CD].
Слайд 28
Для прямых общего положения необходимым и достаточным условием является, чтобы точки
пересечения одноименных проекций находились на одной линии связи.
Но если одна из прямых параллельна плоскости проекции (например, W) и не дана проекция на эту плоскость, то нельзя утверждать, что такие прямые пересекаются.
Но если одна из прямых параллельна плоскости проекции (например, W) и не дана проекция на эту плоскость, то нельзя утверждать, что такие прямые пересекаются.
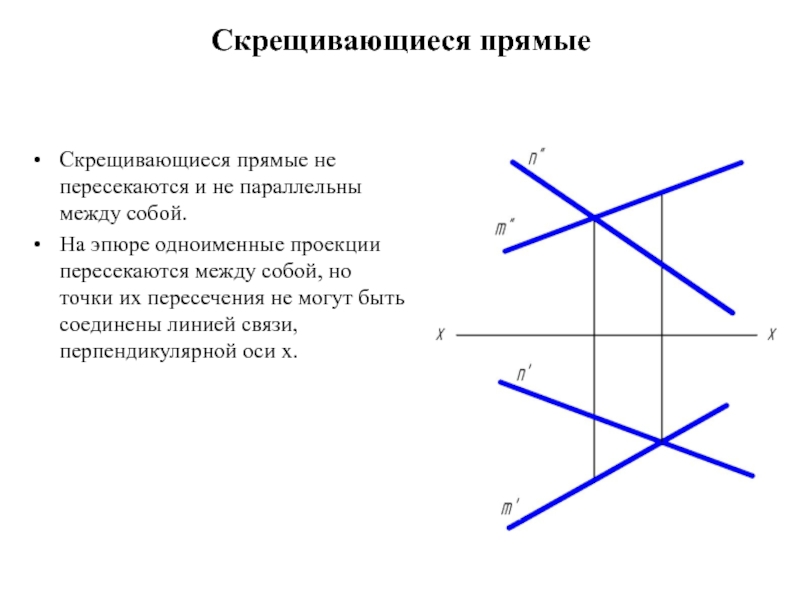
Слайд 31Скрещивающиеся прямые
Скрещивающиеся прямые не пересекаются и не параллельны между собой.
На эпюре
одноименные проекции пересекаются между собой, но точки их пересечения не могут быть соединены линией связи, перпендикулярной оси х.
Слайд 32
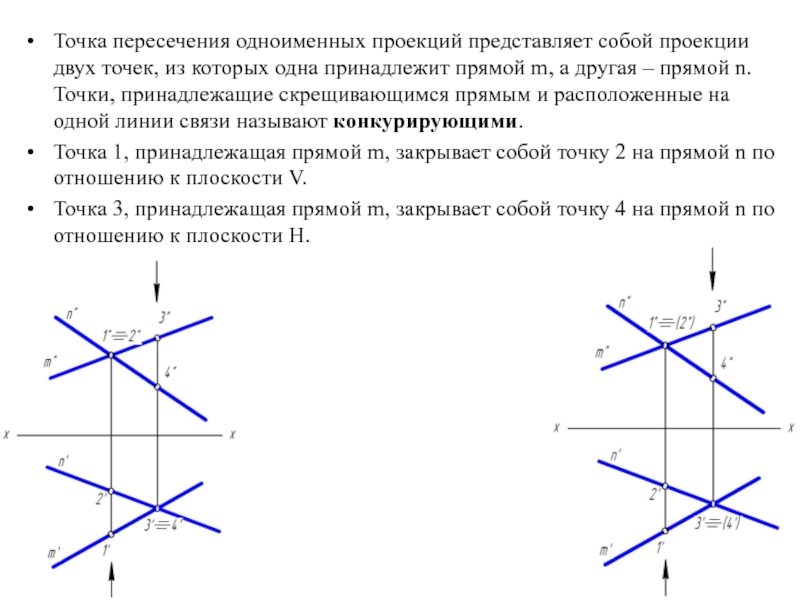
Точка пересечения одноименных проекций представляет собой проекции двух точек, из которых
одна принадлежит прямой m, а другая – прямой n. Точки, принадлежащие скрещивающимся прямым и расположенные на одной линии связи называют конкурирующими.
Точка 1, принадлежащая прямой m, закрывает собой точку 2 на прямой n по отношению к плоскости V.
Точка 3, принадлежащая прямой m, закрывает собой точку 4 на прямой n по отношению к плоскости Н.
Точка 1, принадлежащая прямой m, закрывает собой точку 2 на прямой n по отношению к плоскости V.
Точка 3, принадлежащая прямой m, закрывает собой точку 4 на прямой n по отношению к плоскости Н.
Слайд 33Свойства проекций плоских углов
1. Если стороны угла не параллельны плоскости проекции,
то угол проецируется на эту плоскость с искажением.
2. Если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол (тупой, прямой, острый).
3. Если обе стороны любого угла параллельны плоскости проекции, то на эту плоскость он проецируется без искажения.
4. Проекции острого и тупого углов могут проецироваться на плоскость проекции без искажения не только при условии параллельности сторон угла плоскости проекции.
5. Если стороны угла параллельны плоскости проекции или одинаково наклонены к ней, то деление пополам проекции угла соответствует его делению пополам в пространстве.
Частный случай проецирования прямого угла: Если одна сторона прямого угла параллельна плоскости проекции, то на эту плоскость проекции прямой угол проецируется без искажения.
2. Если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол (тупой, прямой, острый).
3. Если обе стороны любого угла параллельны плоскости проекции, то на эту плоскость он проецируется без искажения.
4. Проекции острого и тупого углов могут проецироваться на плоскость проекции без искажения не только при условии параллельности сторон угла плоскости проекции.
5. Если стороны угла параллельны плоскости проекции или одинаково наклонены к ней, то деление пополам проекции угла соответствует его делению пополам в пространстве.
Частный случай проецирования прямого угла: Если одна сторона прямого угла параллельна плоскости проекции, то на эту плоскость проекции прямой угол проецируется без искажения.
Слайд 35
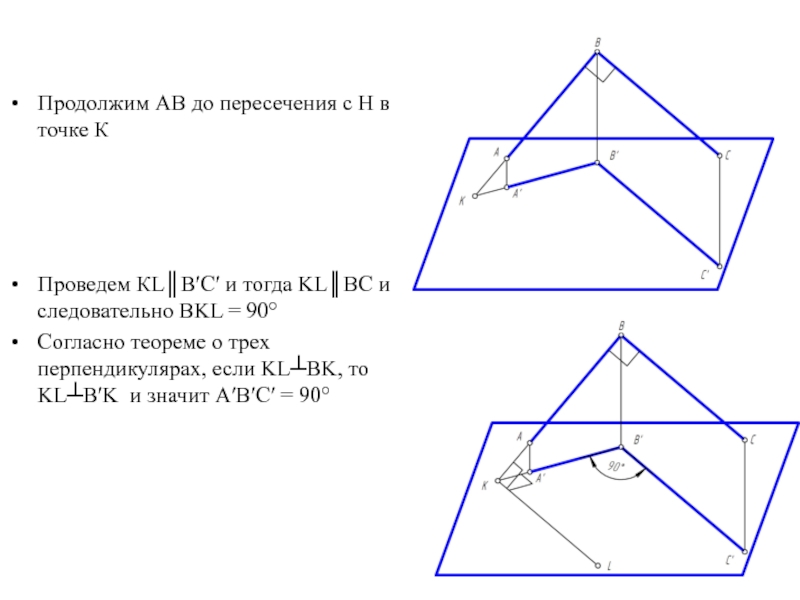
Продолжим АВ до пересечения с Н в точке К
Проведем КL║B′C′ и
тогда KL║BC и следовательно BKL = 90°
Согласно теореме о трех перпендикулярах, если KL┴BK, то KL┴B′K и значит А′В′С′ = 90°
Согласно теореме о трех перпендикулярах, если KL┴BK, то KL┴B′K и значит А′В′С′ = 90°







![Достроить фронтальную проекцию отрезка CD, пересекающего отрезок АВ в точке К.Точка К принадлежит [АВ]; Точка](/img/tmb/3/257547/3ce3269edb514c87bd103dde10eedd1a-800x.jpg)