- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Гаусcа та її застосування презентация
Содержание
- 1. Теорема Гаусcа та її застосування
- 2. Лекція 15 Теорема Гаусcа та її застосування.
- 3. Всі науки можна класифікувати на дві групи: Фізика. Колекціонування марок. Ернест Резерфорд
- 4. Потік вектора напруженості електричного поля. Теорема
- 5. Лекція 15 Теорема Гаусса Потік вектора
- 6. Лекція 15 Теорема Гаусса Потік вектора
- 7. Лекція 15 Теорема Гаусса Теорема Гаусса
- 8. Лекція 15 Теорема Гаусса Теорема Гаусса
- 9. Лекція 15 Теорема Гаусса Приклади розрахунку
- 10. Лекція 15
- 11. Лекція 15 Теорема Гаусса Приклади розрахунку
- 12. Напруженість поля нескінченної зарядженої нитки,
- 13. Напруженість поля нескінченної зарядженої нитки, довгого
- 14. Напруженість поля нескінченного довгого діелектричного циліндра
- 15. Напруженість поля нескінченного довгого діелектричного циліндра
- 16. Напруженість поля рівномірно зарядженої сфери
- 17. Напруженість поля рівномірно зарядженої сфери Лекція
- 19. Напруженість поля непровідної кулі Лекція 15
- 20. Дивергенцією деякого векторного поля
- 21. Лекція 15 Теорема Гаусса
- 22. Елементарна робота сил електростатичного поля Для поля точкового заряду Лекція 15 Теорема Гаусса
- 23. Робота сил електростатичного поля точкового заряду при
- 24. Робота електростатичного поля не залежить від
- 26. Дякую за увагу!
Лекція 15
Теорема Гаусcа та її застосування.
Слайд 4Потік вектора напруженості електричного поля.
Теорема Остроградського-Гаусса.
Застосування теореми Остроградського-Гаусса до
розрахунку електричних полів.
Теорема Гаусса у диференціальній формі.
Робота сил електростатичного поля.
Теорема Гаусса у диференціальній формі.
Робота сил електростатичного поля.
План лекції
Слайд 6Лекція 15
Теорема Гаусса
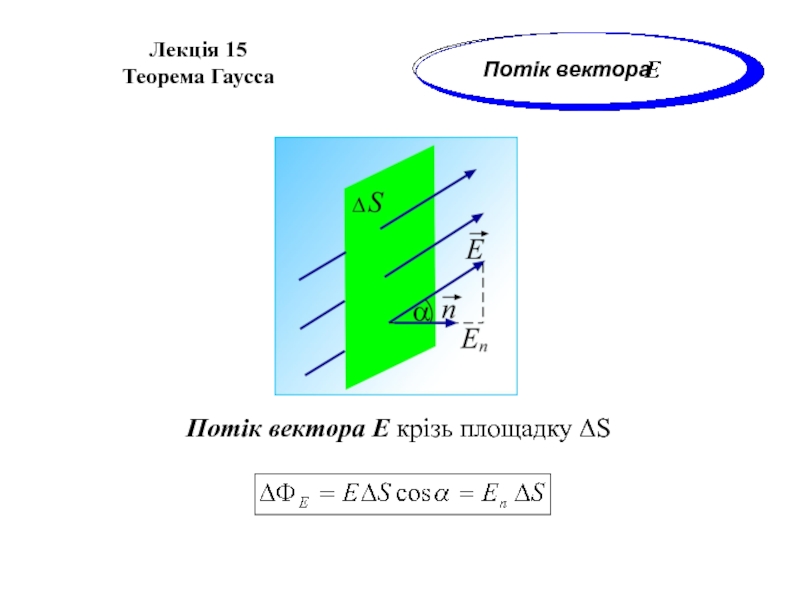
Потік вектора E
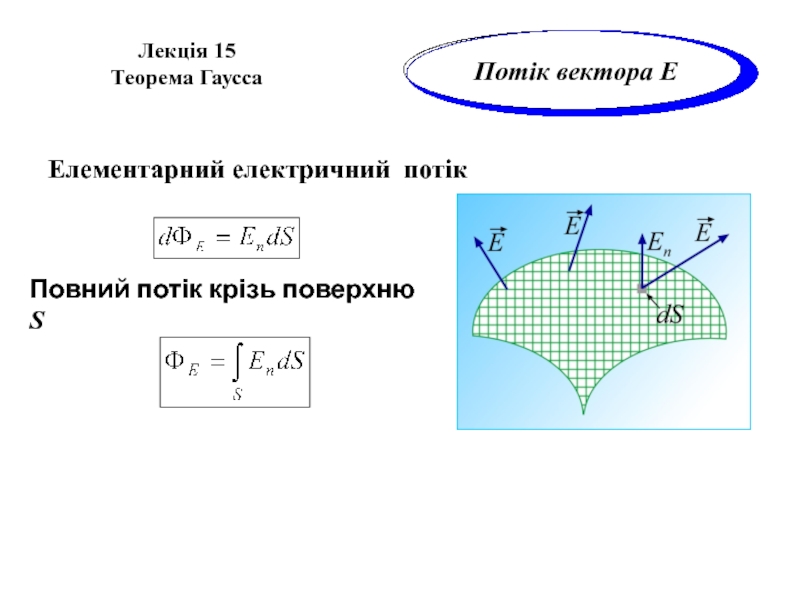
Елементарний електричний потік
Повний потік крізь
поверхню S
Слайд 7Лекція 15
Теорема Гаусса
Теорема Гаусса
Гаусс Карл Фрідріх,
(1777-1855)
Німецький математик і фізик.
Роботи
з алгебри, теорії чисел, диференціальної геометрії і теорії чисел, електрики і магнетизму, астрономії.
Слайд 8Лекція 15
Теорема Гаусса
Теорема Гаусса
Потік вектора напруженості
електростатичного поля у
вакуумі крізь довільну замкнену поверхню S зсередини назовні дорівнює алгебричній сумі тих точкових зарядів , які охоплюються поверхнею S, поділеній на електричну сталу .
Слайд 9Лекція 15
Теорема Гаусса
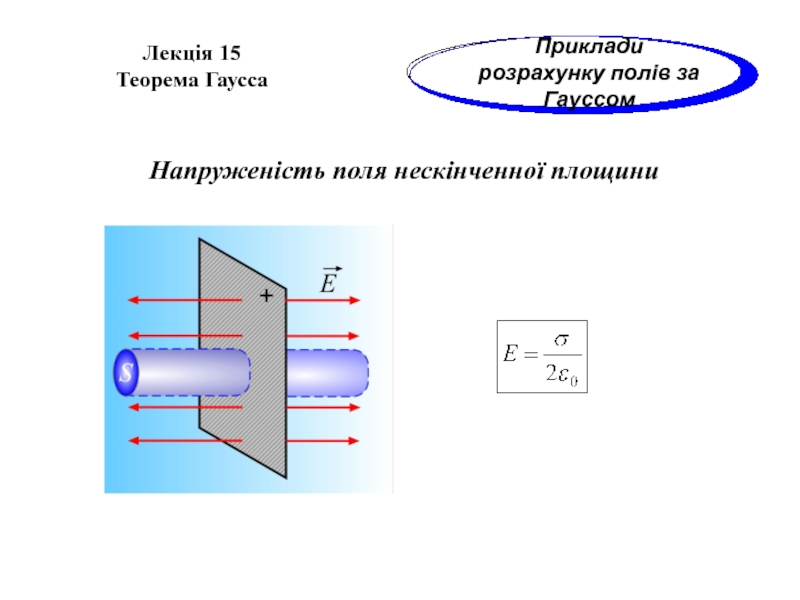
Приклади розрахунку полів за Гауссом
Напруженість поля нескінченної
площини
Слайд 10
Лекція 15
Теорема Гаусса
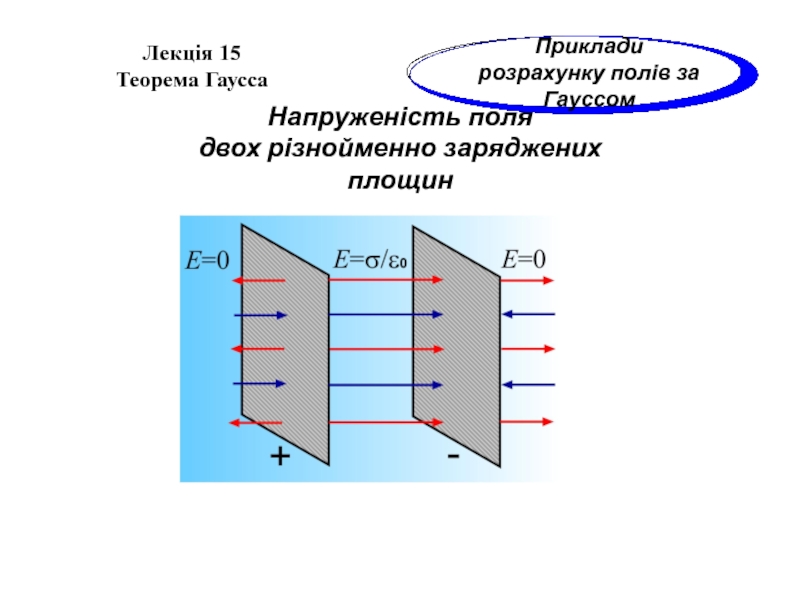
Приклади розрахунку полів за Гауссом
Напруженість поля
двох
різнойменно заряджених площин
Слайд 11Лекція 15
Теорема Гаусса
Приклади розрахунку полів за Гауссом
Напруженість поля
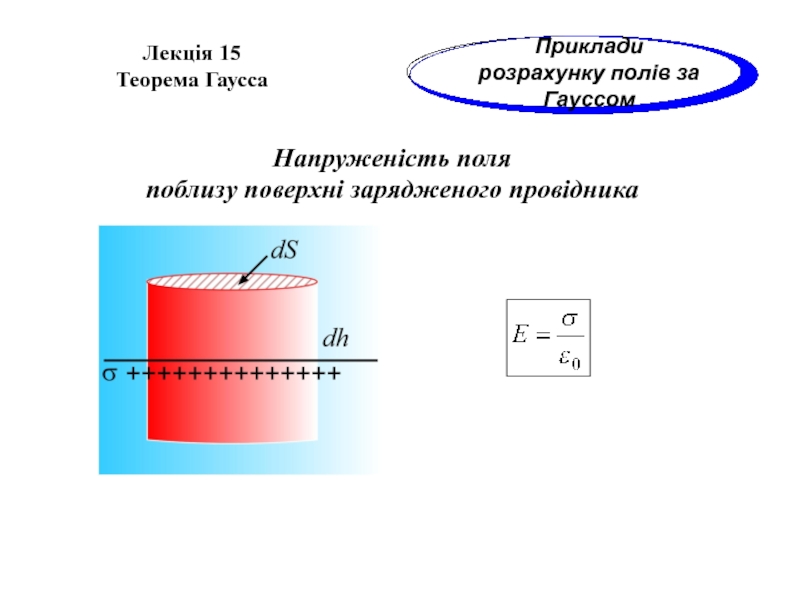
поблизу
поверхні зарядженого провідника
Слайд 12
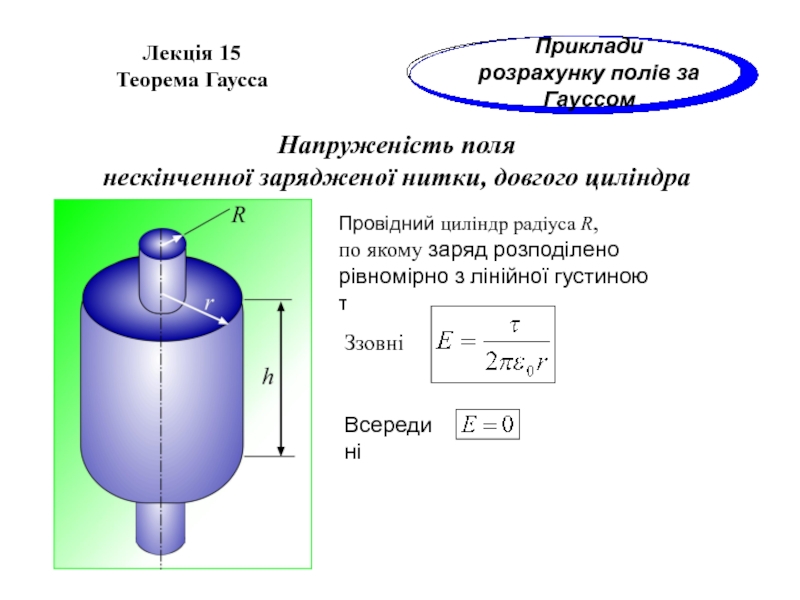
Напруженість поля
нескінченної зарядженої нитки, довгого циліндра
Провідний циліндр радіуса R,
по якому заряд розподілено
рівномірно з лінійної густиною τ
Ззовні
Всередині
Лекція 15
Теорема Гаусса
Приклади розрахунку полів за Гауссом
Слайд 13Напруженість поля
нескінченної зарядженої нитки, довгого циліндра
Лекція 15
Теорема Гаусса
Приклади
розрахунку полів за Гауссом
Слайд 14Напруженість поля
нескінченного довгого діелектричного циліндра
Лекція 15
Теорема Гаусса
Приклади розрахунку полів
за Гауссом
Непровідний циліндр радіуса R, в якому заряд розподілено рівномірно з об’ємною густиною ρ
Ззовні циліндра
Всередині циліндра
Слайд 15Напруженість поля
нескінченного довгого діелектричного циліндра
Лекція 15
Теорема Гаусса
Приклади розрахунку полів
за Гауссом
Слайд 16
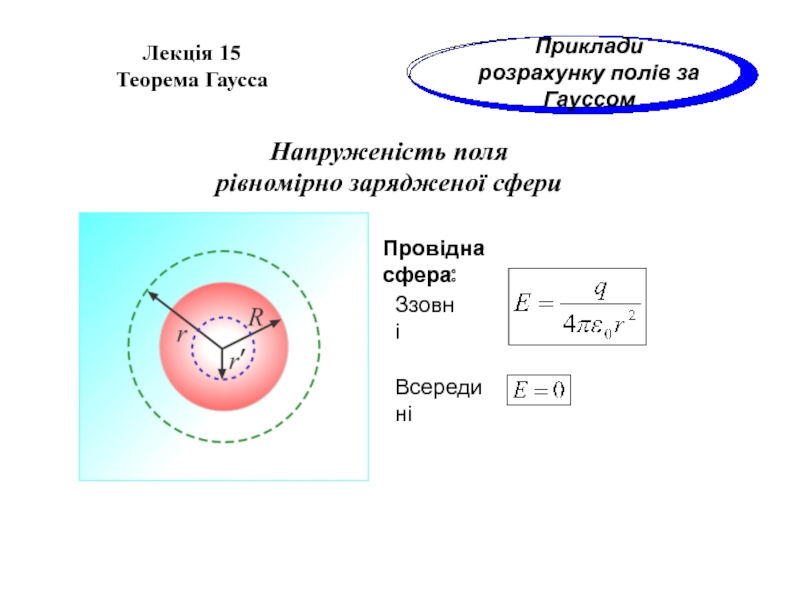
Напруженість поля
рівномірно зарядженої сфери
Провідна сфера:
Ззовні
Всередині
Лекція 15
Теорема Гаусса
Приклади розрахунку полів
за Гауссом
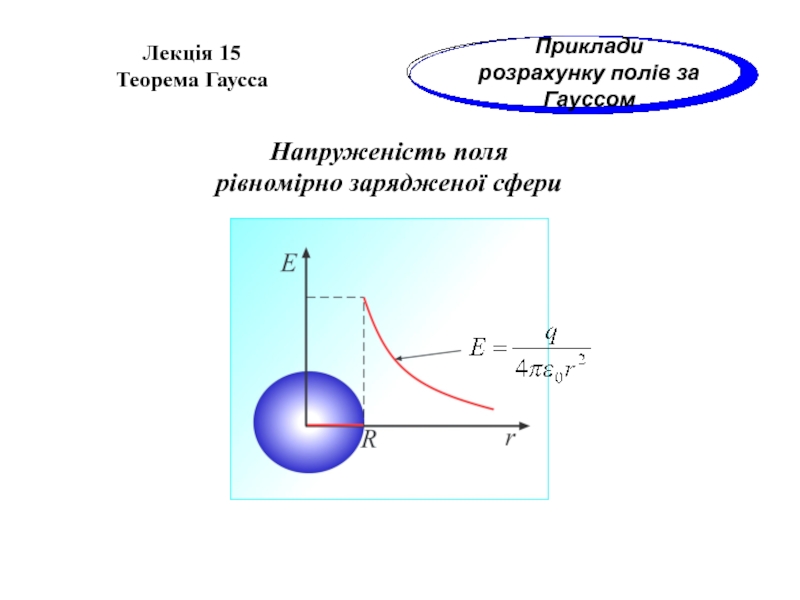
Слайд 17Напруженість поля
рівномірно зарядженої сфери
Лекція 15
Теорема Гаусса
Приклади розрахунку полів за
Гауссом
Слайд 18
Напруженість поля
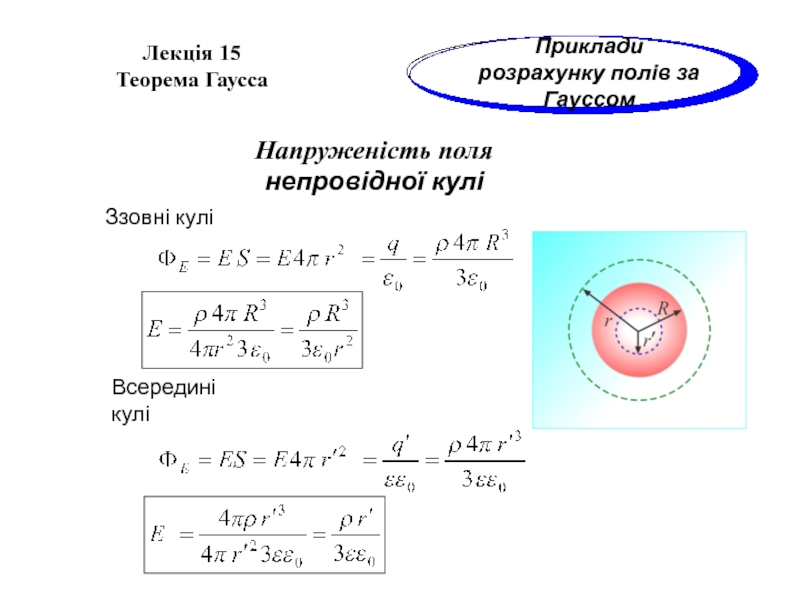
непровідної кулі
Лекція 15
Теорема Гаусса
Приклади розрахунку полів за Гауссом
Ззовні кулі
Всередині кулі
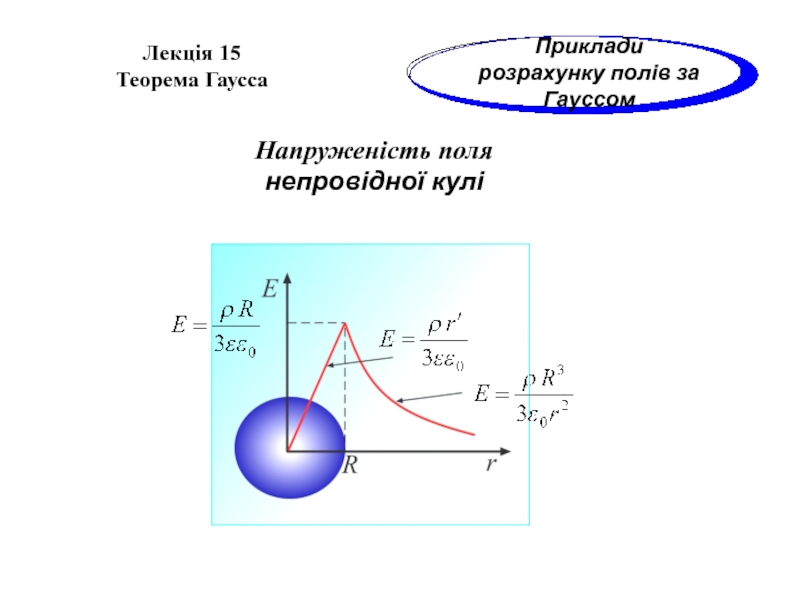
Слайд 19Напруженість поля
непровідної кулі
Лекція 15
Теорема Гаусса
Приклади розрахунку полів за Гауссом
Слайд 20Дивергенцією деякого векторного поля називається границя відношення
У декартовій системі координат
Лекція 15
Теорема Гаусса
Поняття дивергенції
Слайд 21
Лекція 15
Теорема Гаусса
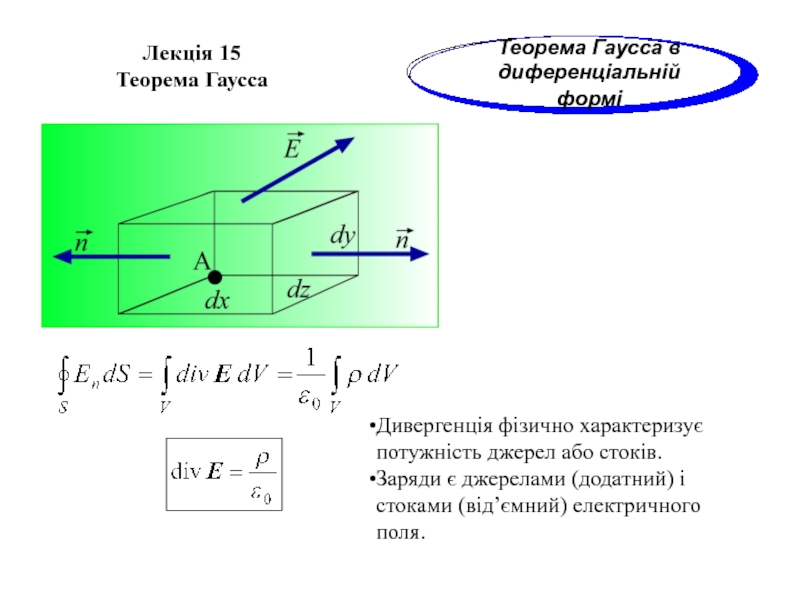
Теорема Гаусса в диференціальній формі
Дивергенція фізично характеризує
потужність джерел або стоків.
Заряди є джерелами (додатний) і стоками (від’ємний) електричного поля.
Заряди є джерелами (додатний) і стоками (від’ємний) електричного поля.
Слайд 22Елементарна робота сил електростатичного поля
Для поля точкового заряду
Лекція 15
Теорема Гаусса
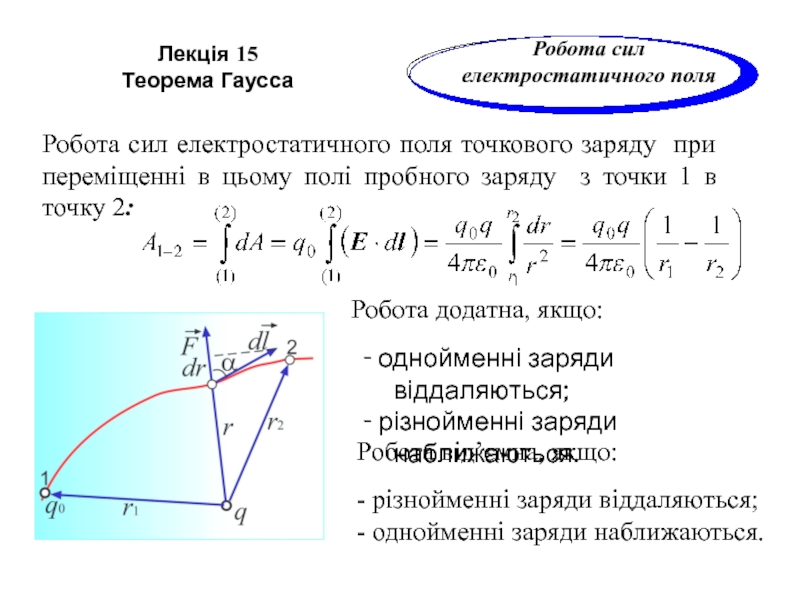
Слайд 23Робота сил електростатичного поля точкового заряду при переміщенні в цьому полі
пробного заряду з точки 1 в точку 2:
Лекція 15
Теорема Гаусса
Робота додатна, якщо:
Робота від’ємна, якщо:
- різнойменні заряди віддаляються;
- однойменні заряди наближаються.
- однойменні заряди віддаляються;
- різнойменні заряди наближаються.
Слайд 24 Робота електростатичного поля не залежить від форми шляху переміщення заряду
від точки 1 до точки 2, а визначається лише положенням початкової і кінцевої точки.
Лекція 3
Потенціал електростатичного
поля
Силові поля, що задовольняють таку умову, називаються потенціальними, або консервативними
