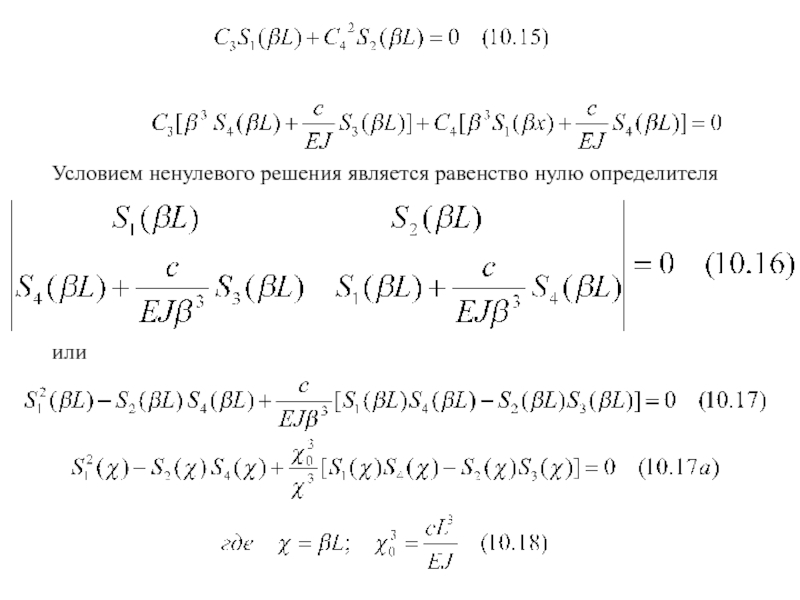- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Колебания линейных распределенных систем презентация
Содержание
- 1. Колебания линейных распределенных систем
- 2. Семинар 11. Изгибные колебания стержня
- 3. В технической теории изгибные колебания стержня описывают
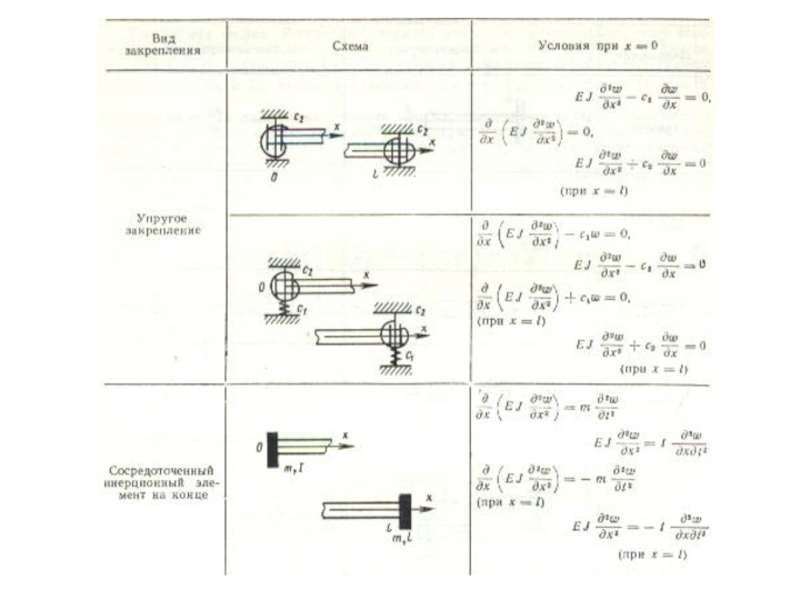
- 4. Основные типы краевых условий для изгибных колебаний стержней
- 7. Пример 1. Определить собственную частоты и формы
- 8. Общее решение в виде Подстановка (10.14) в
- 9. Условием ненулевого решения является равенство нулю определителя или
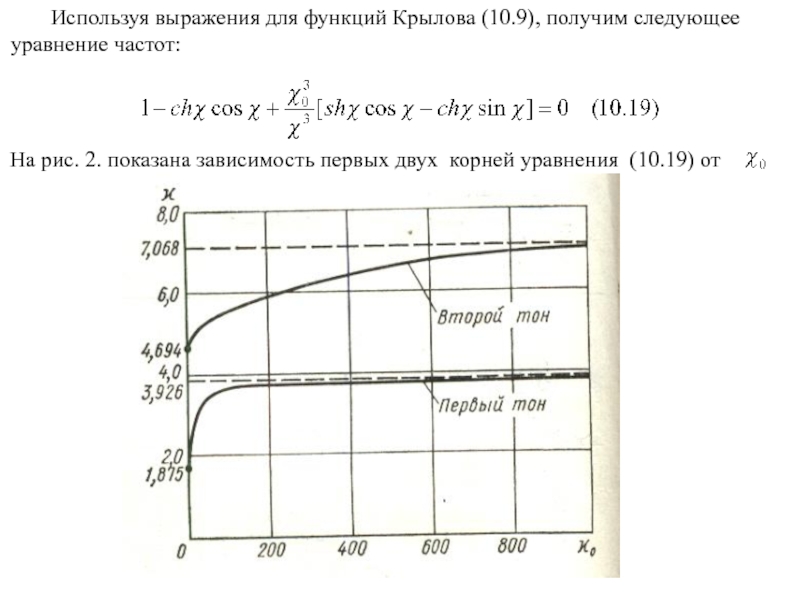
- 10. Используя выражения для функций Крылова (10.9), получим
- 11. Если
Слайд 3 В технической теории изгибные колебания стержня описывают уравнением при p =
Если стержень имеет постоянные по длине характеристики EJ = const,
рF = const, то уравнение для исследования собственных колебаний будет следующим:
Функция w(x, t) на концах стержня должна удовлетворять краевым условиям, соответствующим характеру закрепления концов стержня.
Слайд 7 Пример 1. Определить собственную частоты и формы изгибных колебаний стержня
Подстановка (10.3)
L
EJ
Начальные условия для определения собственных частот всегда нулевые
Граничные условия при x =0 и x = L для W(x)
Решение уравнения имеет вид
c
Слайд 8 Общее решение в виде
Подстановка (10.14) в последние два условия (10.13)
Два
Производные
Слайд 10 Используя выражения для функций Крылова (10.9), получим следующее уравнение частот:
На рис.
Слайд 11Если
Форма колебаний определяется функцией
Балочные функции. Собственные формы изгибных колебаний стержней с постоянными по длине характеристиками для различных краевых условий называют балочными функциями.
Так, формула 10.21) определяет балочную функцию для стержня с одним заделанным и другим опертым на линейную пружину концом.