- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 1. Понятие рынка ценных бумаг и его инструментов презентация
Содержание
- 1. Тема 1. Понятие рынка ценных бумаг и его инструментов
- 2. Тема 1. Понятие рынка ценных бумаг и его инструментов
- 3. Что же такое рынок ценных бумаг? Ры́нок
- 4. Первичный и вторичный рынки ценных
- 5. Первичный и вторичный рынки ценных
- 6. Инструменты торгуемые на рынке ценных бумаг
- 7. Облигации Облигация — это ценная бумага, удостоверяющая
- 8. Акции Акция — в соответствии с законом
- 9. Вексель - ценная бумага, удостоверяющая письменное денежное
- 10. Чек - ценная бумага, удостоверяющая письменное поручение
- 11. Банковский сертификат — ценная бумага, представляющая собой
- 12. Коносамент - ценная бумага, представляющая собой документ
- 13. Закладная - это именная ценная бумага, удостоверяющая
- 14. Инвестиционный пай - именная ценная бумага, удостоверяющая
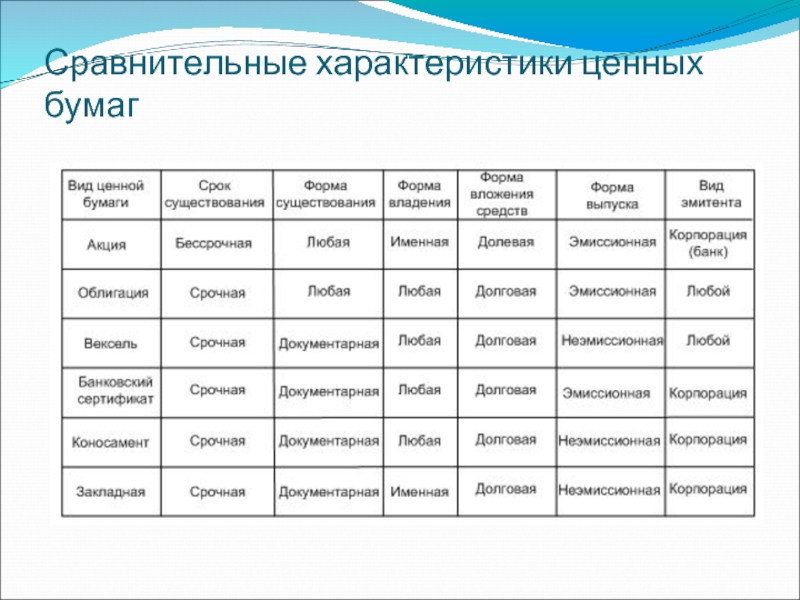
- 15. Сравнительные характеристики ценных бумаг
- 16. Виды ценных бумаг и их классификация
- 17. Виды ценных бумаг и их классификация
- 18. Виды ценных бумаг и их классификация
- 19. Виды анализа
- 20. Тема 2. Формирование портфеля ценных бумаг и управление им
- 21. Определение портфеля ценных бумаг
- 22. Портфельное инвестирование, типы портфелей инвесторов
- 23. Портфельное инвестирование, типы портфелей инвесторов
- 24. Эффективность портфеля где Сt+1 - цена продажи
- 25. Эффективность портфеля В качестве меры риска, считая
- 26. Эффективность портфеля Портфели, лежащие правее, имеют больший
- 27. Эффективность портфеля В САРМ-модели предполагается, что эффективность
- 28. Хеджирование портфеля ценных бумаг Индексная модель Шарпа:
- 29. Хеджирование портфеля ценных бумаг Хеджирование инвестиционного портфеля
- 30. Портфель облигаций. Иммунизация портфеля облигаций Рыночная стоимость
- 31. Портфель облигаций. Иммунизация портфеля облигаций Дюрация
- 32. Конец лекции №1
Слайд 3Что же такое рынок ценных бумаг?
Ры́нок це́нных бума́г, фо́ндовый ры́нок (англ.
Слайд 4Первичный и вторичный
рынки ценных бумаг
Первичный рынок ценных бумаг —
Первичное размещение бывает двух видов — частное и публичное.
Частное размещение (англ. private placement). В этом случае пакет ценных бумаг продается ограниченному числу лиц (как правило, одному-двум институциональным инвесторам). Особенностью частного размещения является закрытый характер сделки. Никаких требований по раскрытию финансовой документации не предъявляется.
Публичное размещение (англ. public offering) или IPO (initial public offering (англ.)). Публичное размещение происходит с помощью посредников. Ими могут выступать как биржи, так и институциональные брокеры
Слайд 5Первичный и вторичный
рынки ценных бумаг
Вторичный рынок ценных бумаг —
Являясь механизмом перепродажи, он позволяет инвесторам свободно покупать и продавать бумаги. При отсутствии вторичного рынка или его слабой организации последующая перепродажа ценных бумаг была бы невозможна или затруднена, что оттолкнуло бы инвесторов от покупки всех или части бумаг. В итоге общество осталось бы в проигрыше, так как многие, особенно новейшие, начинания не получили бы необходимой финансовой поддержки.
Слайд 7Облигации
Облигация — это ценная бумага, удостоверяющая единичное долговое обязательство эмитента (государства
Слайд 8Акции
Акция — в соответствии с законом РФ «О рынке ценных бумаг»
Экономическое определение — это ценная бумага, удостоверяющая единичный вклад в уставный капитал коммерческого товарищества с вытекающими из этого правами для ее владельца.
Слайд 9Вексель - ценная бумага, удостоверяющая письменное денежное обязательство должника о возврате
Простой вексель - это ценная бумага, удостоверяющая безусловное обязательство (обещание) должника уплатить указанную в нем сумму денег векселедержателю через определенный срок времени;
Переводной вексель — это ценная бумага, удостоверяющая предложение должнику уплатить указанную в ней сумму денег обозначенному в ней лицу через определенный срок
Вексель.
Слайд 10Чек - ценная бумага, удостоверяющая письменное поручение чекодателя банку уплатить чекополучателю
Чек.
Слайд 11Банковский сертификат — ценная бумага, представляющая собой свободно обращающееся свидетельство о
Банковский сертификат.
Слайд 12Коносамент - ценная бумага, представляющая собой документ стандартной формы, принятой в
Коносамент.
Слайд 13Закладная - это именная ценная бумага, удостоверяющая права ее владельца в
Закладная.
Слайд 14Инвестиционный пай - именная ценная бумага, удостоверяющая долю его владельца в
Инвестиционный пай
Слайд 24Эффективность портфеля
где Сt+1 - цена продажи бумаги в (t + 1)-й
Сt - цена покупки бумаги в t-й момент времени.
Ожидаемой эффективностью (эффектом) будем считать математическое ожидание случайной величины X:
m=Е(Х).
Предположим, что инвестор купил какую-либо ценную бумагу по известной цене и через некоторое время намеревается продать ее по заранее не известной цене, а также за время владения этой бумагой инвестор рассчитывает получить дивиденды в неизвестном объеме
Слайд 25Эффективность портфеля
В качестве меры риска, считая эффективность некоторой ценной бумаги случайной
можно принять ее вариацию (дисперсию)
Для моделирования портфеля важное значение будет иметь величина стандартного (
среднеквадратичного) отклонения
и ковариация двух случайных величин X1, X2:
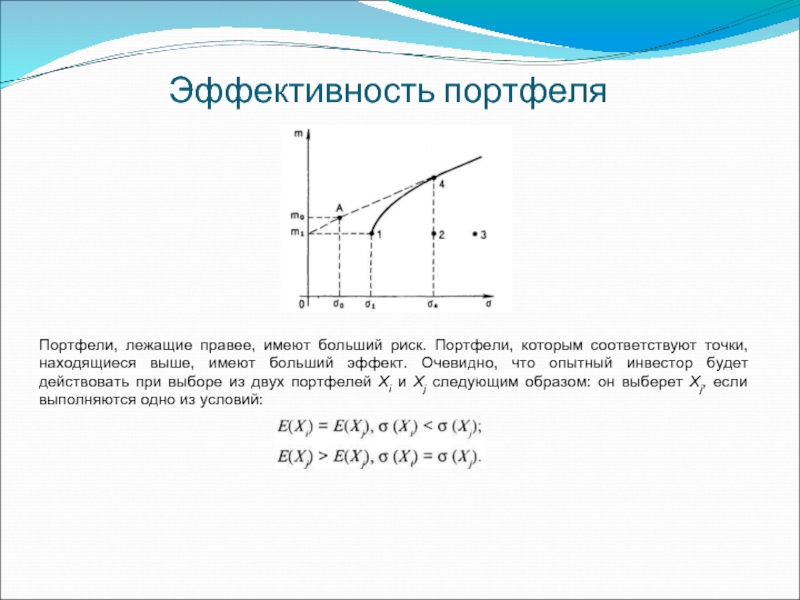
Слайд 26Эффективность портфеля
Портфели, лежащие правее, имеют больший риск. Портфели, которым соответствуют точки,
Слайд 27Эффективность портфеля
В САРМ-модели предполагается, что эффективность ценной бумаги X. линейно зависит
ведущего фактора F, описывающего эффективность рынка в целом, и в то же время на каждую ценную
бумагу влияют и специфические для нее факторы, являющиеся случайными величинами е. Тогда
где αi и βj - некоторые детерминированные величины, а коэффициент βj отражает зависимость
эффективности бумаги от рыночной конъюнктуры, если βj > 0, то эффект бумаги аналогичен эффекту
рынка, если βj < 0, то эффективность бумаги возрастает, когда эффективность рынка снижается.
Для характеристики конкретной ценной бумаги используются и другие параметры. Поскольку вариация
эффективности каждой ценной бумаги состоит из "собственной" и "рыночной" компонент, то величина
где VF - вариация эффективности рынка;
V ej - вариация "собственной" составляющей эффективности бумаги, будет характеризовать долю риска
каждого вклада, вносимую неопределенностью рынка в целом.
Слайд 28Хеджирование портфеля ценных бумаг
Индексная модель Шарпа:
где Xj- ожидаемая доходность (эффективность)
α j - доходность портфеля при условии отсутствия воздействия рыночных факторов;
βj - бета-коэффициент портфеля;
F ~ ожидаемая доходность рыночного портфеля, представленная фондовым рыночным индексом;
еj - ошибка, являющаяся независимой случайной переменной с постоянной дисперсией и нулевым математическим ожиданием, ее ковариации с остальными случайными переменными, входящими в уравнение, равны нулю
В целом для портфеля акций можно записать:
Бета-коэффициент характеризует рыночный (систематический, не диверсифицируемый) риск портфеля, для устранения которого и могут использоваться фьючерсные и опционные контракты на фондовый индекс. Для изучения хеджирования портфеля акций рассмотрим модельный фондовый индекс 1п, рассчитанный по курсам акций L эмитентов для n-го момента времени:
где In - текущее значение индекса;
In-1 - значение индекса на предыдущих торгах (примем I0 = 100);
RKn и RKn-1 - суммарная рыночная капитализация акций L эмитентов, входящих в расчет индекса,
по п-м и (n-1)-м торгам.
Слайд 29Хеджирование портфеля ценных бумаг
Хеджирование инвестиционного портфеля акций - процесс снижения риска
Диверсификация инвестиционного портфеля акций - процесс снижения риска портфеля путем включения в него слабокоррелированных друг с другом акций.
Слайд 30Портфель облигаций. Иммунизация портфеля облигаций
Рыночная стоимость облигаций
где С - ежегодная купонная
r - внутренняя норма доходности облигации, в нашем случае равная доходности
облигации до погашения;
N - номинал облигации;
T - срок погашения;
Рассмотрим первую производную стоимости облигации
Умножим обе части равенства на (1 + r) / P, получим
Слайд 31Портфель облигаций. Иммунизация портфеля облигаций
Дюрация Макколи:
Преобразуем правую часть равенства. Обозначим через
платежа к текущей стоимости облигации, тогда
Из равенства
следует, что
Таким образом, коэффициент wi является долей цены облигации, которую вносит i-й платеж.
Теперь можно произвести преобразование:
Полученная формула свидетельствует о равенстве эластичности цены облигации средневзвешенному времени погашения облигации