Презентации в PowerPoint

Изобразительная деятельность относится к изобразительному искусству. Искусство – это художественное (образное) отражение человеком окружающего его мира: предметов, явлений природы, общества, себя. Виды детской изобразительной деятельности

Слайд 2. Вступление Метод - это способ достижения цели, основы научных исследований. Значение метода в общественной жизни чрезвычайно высоко. Человек и человечество в целом развиваются, наследуя методы познания, работы, Методы совершенствуются, появляются новые, но некоторые существуют тысячелетиями. Есть точное высказывание

АИС «Юстиция» и ПК «ЕГРП» (выводится из эксплуатации с 01.01.2017) Регистрационные действия по ведению ЕГРП в соответствии с Федеральным законом от 21 июля 1997 г. № 122-ФЗ «О государственной регистрации прав на недвижимое имущество и сделок

Понятие о глобальных проблемах. Причины их обострения. - проблемы и ситуации, которые затрагивают условия жизни и деятельности людей, содержат угрозу для настоящего и будущего. Эти проблемы не могут быть решены силами одной страны, требуют совместно выработанных действий.

НиГМА Независимые Города Молодых Ангарчан Школа – мини - государство Герб государства НиГМА

Хроническая обструктивная болезнь легких (ХОБЛ) ХОБЛ является прогрессирующим заболеванием, незаметно разрушающим легкие. По данным ВОЗ, из-за ХОБЛ ежегодно умирает более 2,75 млн человек. В настоящее время в мире это 4 причина смерти вместе с ВИЧ/СПИДом. Последние эпидемиологические

Основные определения понятия «Юношеский возраст»; Основные задачи развития в юношеском возрасте; Основные периоды юношеского возраста; Психологические трудности юношеского возраста; Основные задачи в процессе физического воспитания; Методы занятий спортом в юношеском возрасте. Содержание: Юношеский возраст: период жизни человека между

Лето. Ласково светит солнце. Все устремляются к морю, к речке, в лес. Природа раскрывает свои объятия. И, глядя на бег реки, кажется, что течение уносит тебя в страну Фантазию. А мой сосед Коля рассказывает всем, что его машинка самая красивая,

Свърши веселото лято есен се задава пак, и звънче училищно ви сбира във вашия прекрасен клас! Всеки нещо ще разкаже, кой какво е преживял, с думички ще обрисува даже спомени безброй видял...

План семинара 1. Важные системные концепции и принципы 2. Предпосылки и история ISO/IEC 15288 3. Стандарт и его процессы Процессы заключения соглашения Организационные процессы обеспечения проектов Проектные процессы Технические процессы Процесс адаптации 4. Управление жизненным циклом Замысел Разработка Производство Использование Поддержка

Vitry-sur-Seine - 15 octobre 2009 P. Теплосети Определение теплосети : - Одна или несколько котельных снабжают по трубам теплом несколько пунктов доставки: - Продажа тепла на основе биномиальной тарификации (абонемент + фактическое потребление,

серебро золото бриллиант вы 400pv = 440у.е. 1,000pv= 1,100у.е. 2,000pv= 2,200у.е. x 2 2,000 у.е. 4,000 у.е. Максимум 3 веток 1у.е. ≈ 0.9 PV большое возн.за развитие сети（в неделю） Каждый имеет право повысить

Мы привыкли видеть постоянно один-два-три памятника воинам-героям, постоянно проходить мимо них в крупных городах и относиться к ним как к чему-либо само собой разумеющемуся. Но на самом деле таких памятников тысячи, десятки тысяч по всей стране и сотни в

300 лет назад в рыбацкой деревушке на севере России, близ г.Холмогоры родился здоровый и крепкий мальчик. Назвали его Михайлой Ломоносовым. Первым учителем Ломоносова была северная природа На парусном судне «Чайка» знакомился с могучей природой и производствами севера

Концепция ресторана «Centre de la terre» Ресторан создан по мотивам научно-фантастического романа французского писателя Жюля Верна «Путешествие к центру земли». Главная цель нашего ресторана – это создание мира полного чудес и неожиданностей. Каждый посетитель

Кроссворд о грибах 1. На бору, на яру стоит мужичок – красный колпачок.

Цели проектирования индивидуальной образовательной траектории ученика обеспечить преемственность между общим и профессиональным образованием. создать условия для дифференциации содержания обучения старшеклассников, построения индивидуальных образовательных программ; обеспечить углубленное изучение отдельных учебных предметов, если это необходимо;

Бактериальный вагиноз (БВ) — заболевание с характерными обильными и продолжительными выделениями из влагалища, нередко с неприятным запахом. В них не обнаруживают гонококков, трихомонад и грибов. Использование термина «бактериальный» обусловлено тем, что заболевание вызвано полимикробной микрофлорой: Микроаэрофильными (Gardnerella vaginalis) Облигатно-анаэробными (Bacteroides

Актуальность Загадка - это очень ёмкое и глубокое литературное произведение, неисчерпаемый источник мудрости, богатства идей, это тот жанр, который необходимо изучать. Цель исследования: Изучить загадки как жанр устного народного творчества.

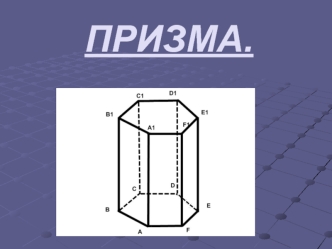
Определение 1. Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой. Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело). Многоугольники, лежащие в параллельных плоскостях, называют основаниями

СТУДИЯ – ПАРИКМАХЕРСКАЯ «VEBER» Находится по адресу город Мыски, улица Ленина, дом 9. Режим работы ежедневно с 10:00 до 19:00 без обеда и выходных В студии – парикмахерской «VEBER» 2 рабочих места

Електричні апарати дистанційного керування до 1000 В Рудникові магнітні пускачі Основні кола схем рудникових пускачів: силове, захисту, керування, взаємного блокування послідовності включення пускачів, джерела живлення кіл захисту і керування.

I ETAP Rejestracja firmy w Urzędzie Miasta Osoby fizyczne oraz wspólnicy spółek cywilnych , którzy mają zamiar rozpocząć działalność gospodarczą muszą złożyć zgłoszenie o wpis do ewidencji działalności gospodarczej. Zgłoszenie do ewidencji zawierać powinno: - imię

Джон Непер Шотландский математик -изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд “Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.