- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цепи переменного тока презентация
Содержание
- 1. Цепи переменного тока
- 2. 2.1. Основные параметры синусоидального сигнала Мгновенное значение
- 3. 2.1. Основные параметры синусоидального сигнала Частота f
- 4. 2.1. Основные параметры синусоидального сигнала Начальная фаза
- 5. 2.1. Основные параметры синусоидального сигнала Действующее (среднеквадратичное)
- 6. 2.2. Способы представления синусоидальных величин Графическое Мгновенное
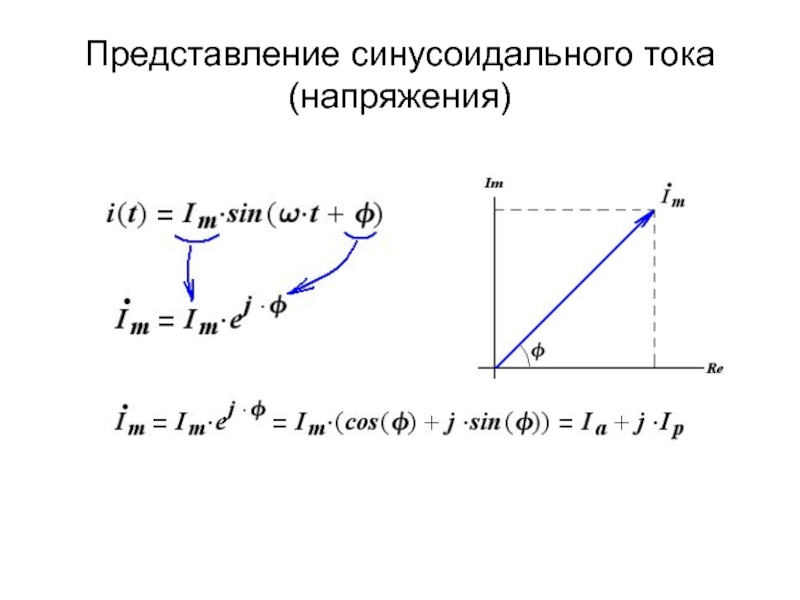
- 7. Представление синусоидального тока (напряжения)
- 8. Шпаргалка
- 9. Шпаргалка-2. Основные операции с комплексными числами 1) 2) 3)
- 10. 2.3. Пассивные элементы в цепи синусоидального тока
- 11. 2.3. Пассивные элементы в цепи синусоидального тока. Резистор Мощность, выделяющаяся на сопротивлении
- 12. 2.3. Пассивные элементы в цепи синусоидального тока.
- 13. 2.3. Пассивные элементы в цепи синусоидального тока.
- 14. 2.3. Пассивные элементы в цепи синусоидального тока.
- 15. 2.3. Пассивные элементы в цепи синусоидального тока.
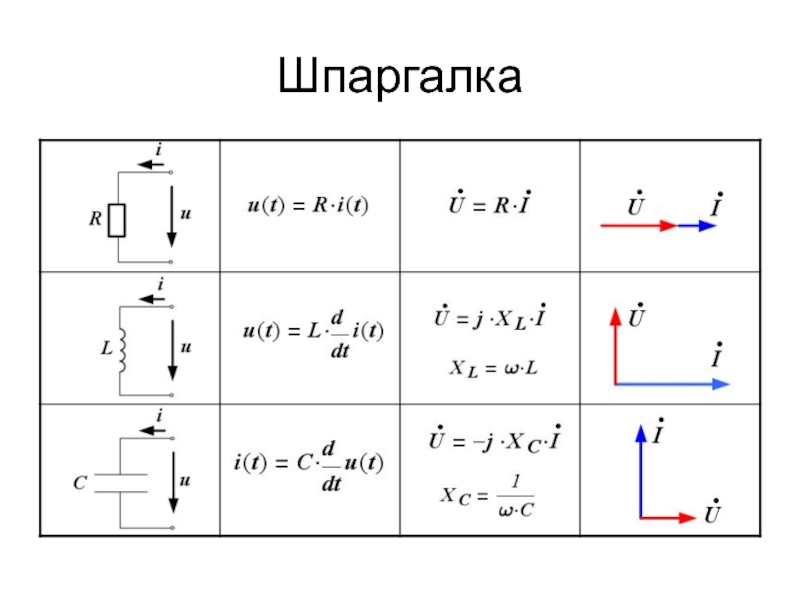
- 16. Шпаргалка
- 17. 2.3. Пассивные элементы в цепи синусоидального тока.
- 18. 2.3. Пассивные элементы в цепи синусоидального тока.
- 19. 2.3. Пассивные элементы в цепи синусоидального тока.
- 20. 2.3. Пассивные элементы в цепи синусоидального тока.
- 21. 2.4. Основные законы в цепях переменного тока
- 22. 2.4. Основные законы в цепях переменного тока
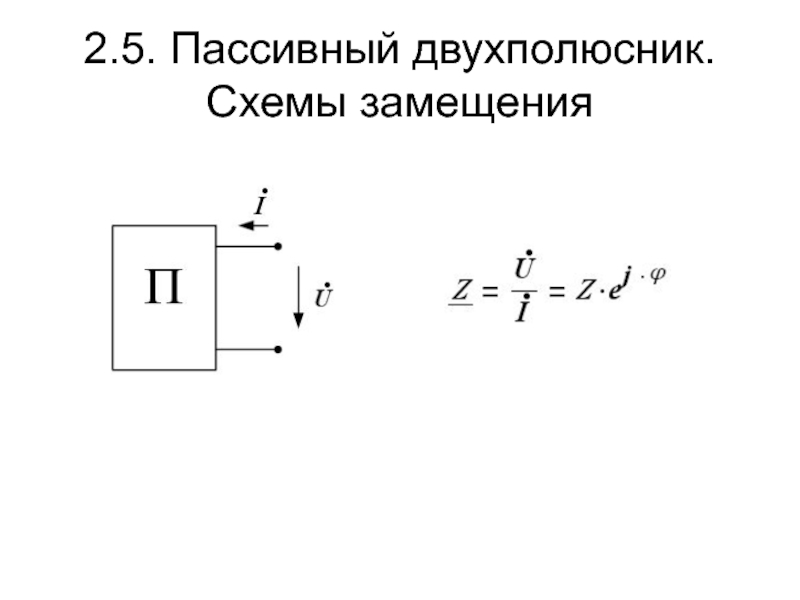
- 23. 2.5. Пассивный двухполюсник. Схемы замещения
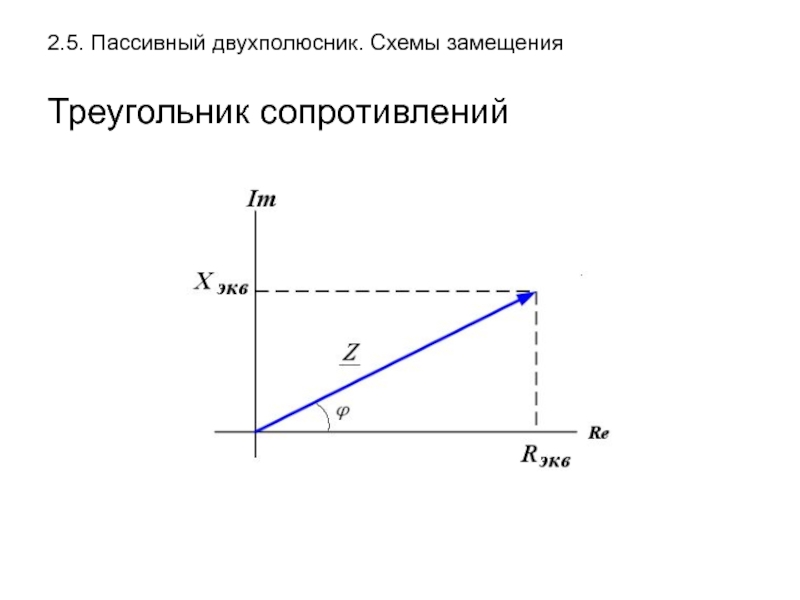
- 24. 2.5. Пассивный двухполюсник. Схемы замещения Треугольник сопротивлений
- 25. 2.5. Пассивный двухполюсник. Схемы замещения Последовательная схема
- 26. 2.5. Пассивный двухполюсник. Схемы замещения Параллельная схема замещения
- 27. 2.5. Пассивный двухполюсник. Схемы замещения Формулы перехода от последовательной к параллельной схеме замещения
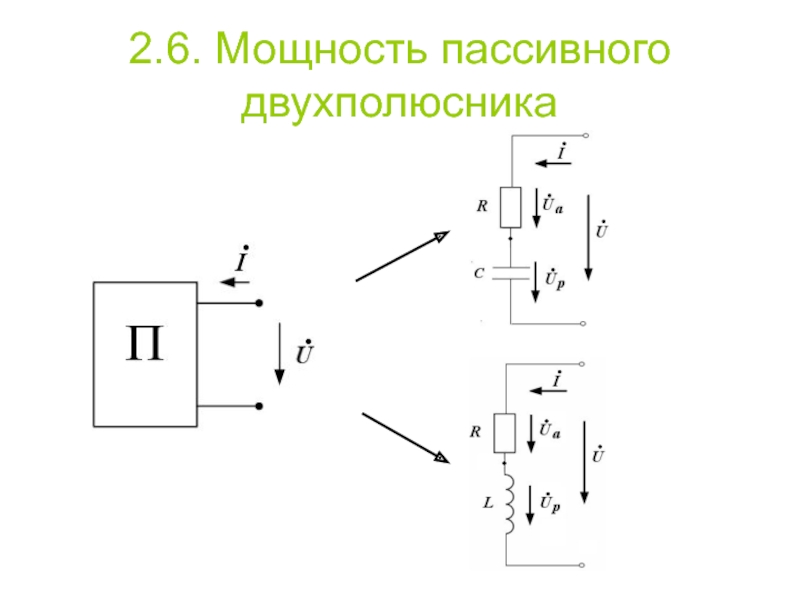
- 28. 2.6. Мощность пассивного двухполюсника
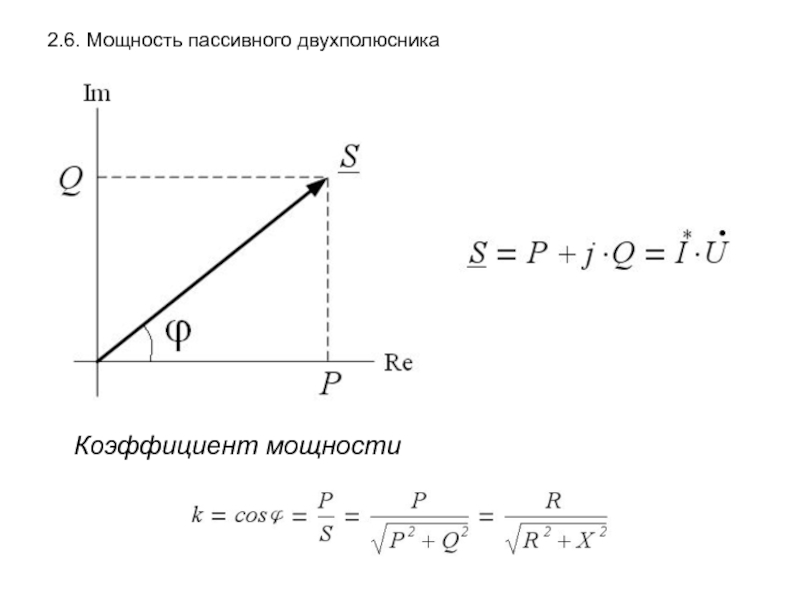
- 29. 2.6. Мощность пассивного двухполюсника Коэффициент мощности
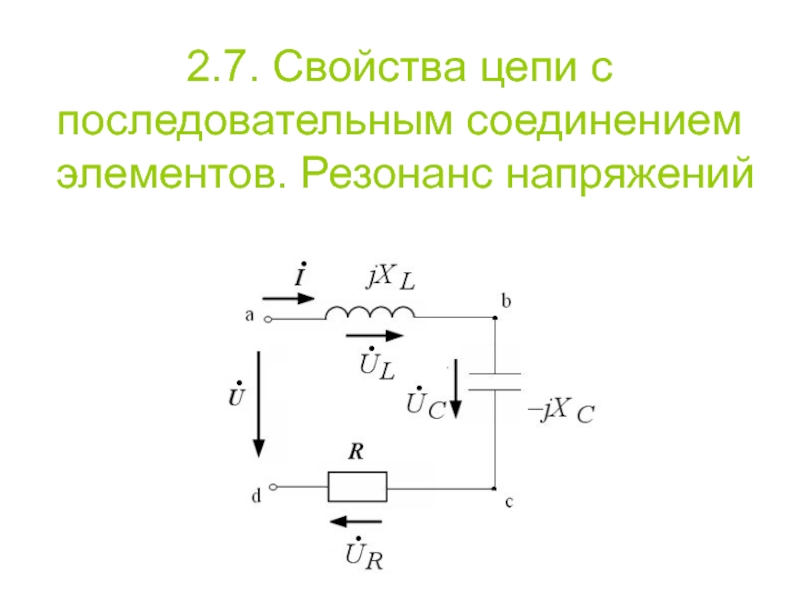
- 30. 2.7. Свойства цепи с последовательным соединением элементов. Резонанс напряжений
- 31. 2.7. Резонанс напряжений Режим, при котором в
- 32. 2.7. Резонанс напряжений Признаки резонанса напряжений:
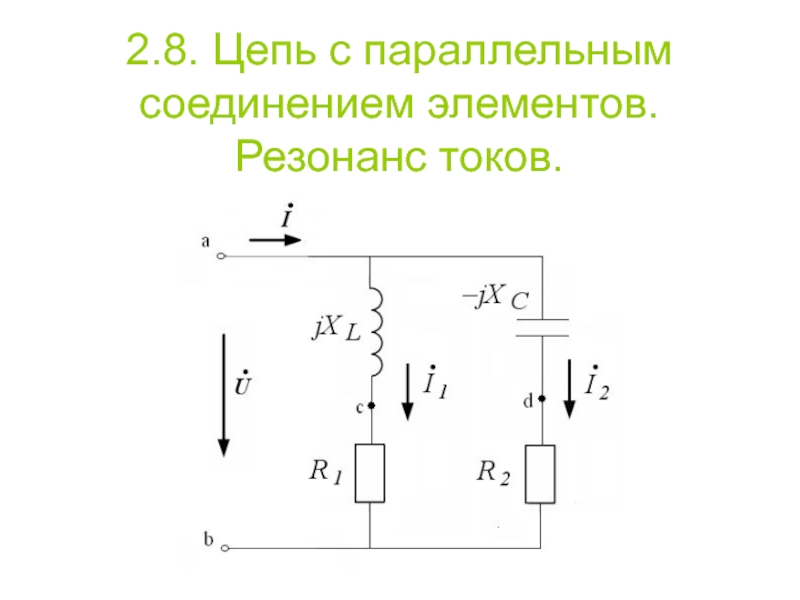
- 33. 2.8. Цепь с параллельным соединением элементов. Резонанс токов.
- 34. 2.8. Резонанс токов Резонансом тока называют режим,
- 35. 2.8. Резонанс токов Признаки резонанса токов 1.
- 36. 2.9. Измерения в цепи переменного тока Измерение
- 37. 2.9. Измерения в цепи переменного тока 3.
- 38. 2.9. Измерения в цепи переменного тока 4.
2.1. Основные параметры синусоидального сигнала Мгновенное значение – значение переменной электрической величины в любой момент времени. Период – наименьший промежуток времени, спустя который все мгновенные значения повторяются. Если F(t) – периодическая
Слайд 22.1. Основные параметры синусоидального сигнала
Мгновенное значение – значение переменной электрической величины
в любой момент времени.
Период – наименьший промежуток времени, спустя который все мгновенные значения повторяются.
Если F(t) – периодическая функция, то
F(t ± T) = F(t),
Где Т - период
Слайд 32.1. Основные параметры синусоидального сигнала
Частота f – величина, обратная периоду
f =
1/ T (Гц)
Амплитуда (максимальное значение)
Фазовый угол в любой момент времени
ω ⋅ t + ϕ
ω -угловая частота
ω = 2⋅ π⋅ f (рад/с)
Амплитуда (максимальное значение)
Фазовый угол в любой момент времени
ω ⋅ t + ϕ
ω -угловая частота
ω = 2⋅ π⋅ f (рад/с)
Слайд 42.1. Основные параметры синусоидального сигнала
Начальная фаза ϕ
= 2⋅ π⋅ f ⋅
Δt,
где Δt – минимальный интервал времени от начала отсчета до ближайшего перехода синусоиды через ноль, причем из отрицательной области в положительную.
где Δt – минимальный интервал времени от начала отсчета до ближайшего перехода синусоиды через ноль, причем из отрицательной области в положительную.
Слайд 52.1. Основные параметры синусоидального сигнала
Действующее (среднеквадратичное) значение
Действующее значение переменного тока равно
по величине такому значению постоянного тока, который, проходя через то же сопротивление, выделяет за период Т такое же количество теплоты, что и синусоидальный ток.
Слайд 62.2. Способы представления синусоидальных величин
Графическое
Мгновенное значение
i(t) = Im⋅ sin(ω⋅ t +
ϕ)
Комплексная форма (показательная форма, алгебраическая, вектор на комплексной плоскости)
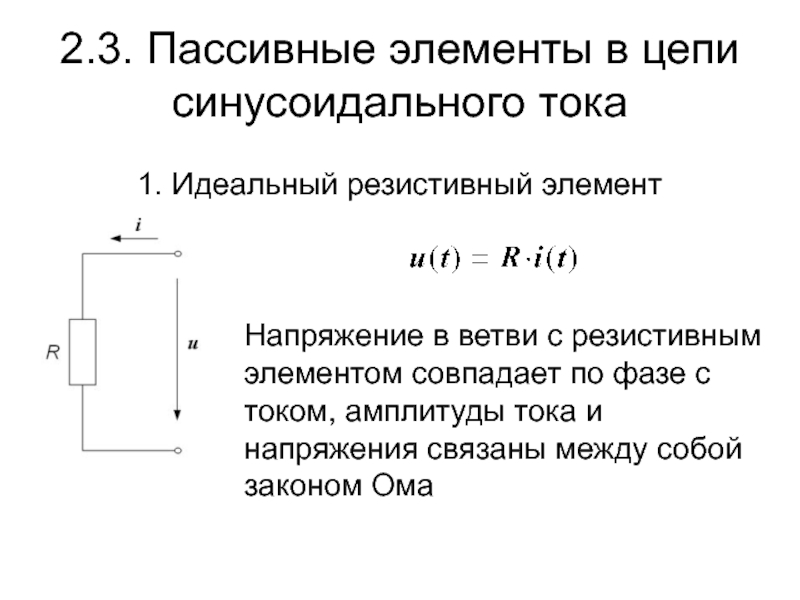
Слайд 102.3. Пассивные элементы в цепи синусоидального тока
1. Идеальный резистивный элемент
Напряжение в
ветви с резистивным элементом совпадает по фазе с током, амплитуды тока и напряжения связаны между собой законом Ома
Слайд 112.3. Пассивные элементы в цепи синусоидального тока. Резистор
Мощность, выделяющаяся на сопротивлении
Слайд 122.3. Пассивные элементы в цепи синусоидального тока.
Идеальный индуктивный элемент
В ветви
с индуктивным элементом ток по фазе отстает на 900 от напряжения, амплитуды тока и напряжения связаны законом Ома
Сопротивление индуктивного элемента является положительным комплексным числом, модуль которого равен ω⋅L
Сопротивление индуктивного элемента является положительным комплексным числом, модуль которого равен ω⋅L
Слайд 132.3. Пассивные элементы в цепи синусоидального тока. Индуктивность
Мощность индуктивного элемента
Активная мощность
Р
= 0
Реактивная мощность
[Q] = вар
Слайд 142.3. Пассивные элементы в цепи синусоидального тока.
Идеальный емкостной элемент
Напряжение отстает
по фазе от тока на 900, амплитуды тока и напряжения связаны законом Ома;
сопротивление емкостного элемента – отрицательное комплексное число, модуль которого равен 1 / ω⋅С.
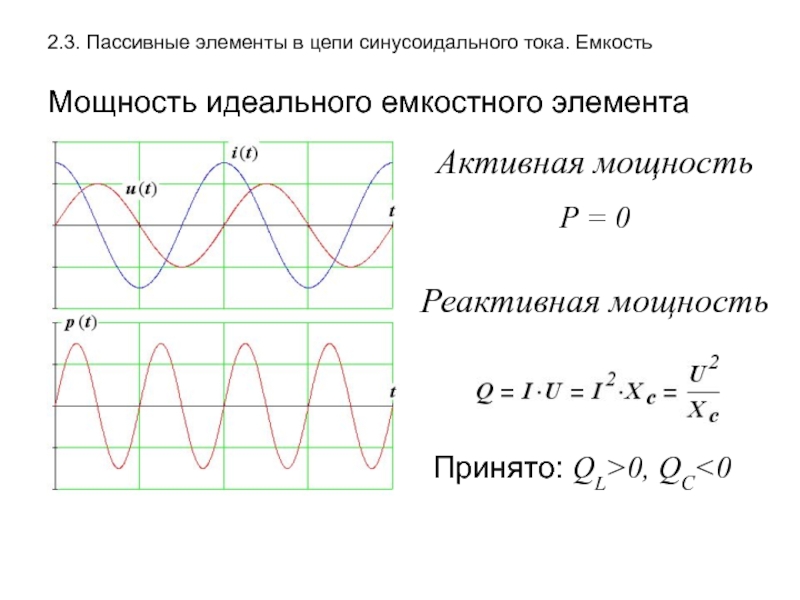
Слайд 152.3. Пассивные элементы в цепи синусоидального тока. Емкость
Мощность идеального емкостного элемента
Активная
мощность
Р = 0
Р = 0
Реактивная мощность
Принято: QL>0, QC<0
Слайд 172.3. Пассивные элементы в цепи синусоидального тока.
Реальный индуктивный элемент
Полное электрическое сопротивление
[Z]
= Ом
Слайд 182.3. Пассивные элементы в цепи синусоидального тока.
Векторная диаграмма состояния цепи
Алгоритм построения
ВТД в последовательной цепи:
1. Принимаем потенциал одной из точек на схеме равным нулю (обычно точка с наименьшим потенциалом).
3. Обходим контур из точки с нулевым потенциалом в направлении увеличения потенциала (против тока) и последовательно строим векторы напряжений на всех элементах цепи (согласно шпаргалке).
2. Выбираем вектор (обычно вектор тока), относительно которого будем отсчитывать фазу векторов. Фазу этого вектора можно принять любой.
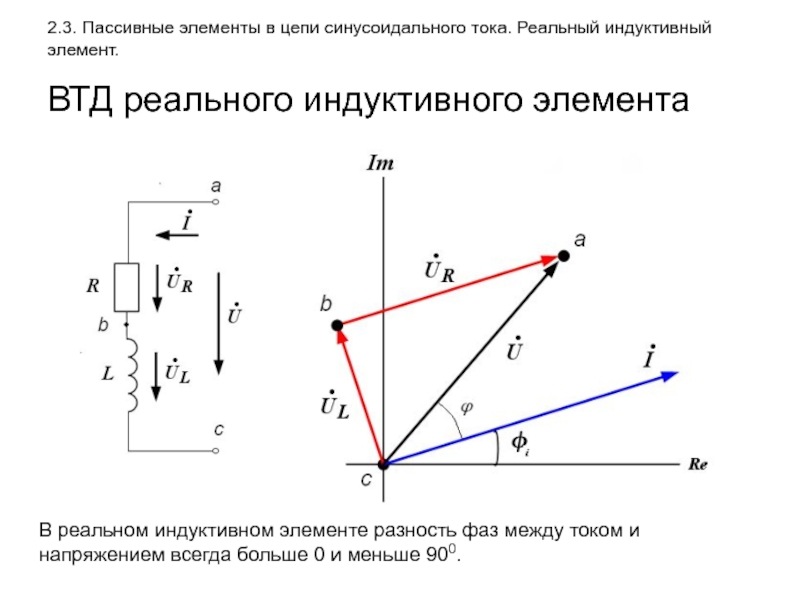
Слайд 192.3. Пассивные элементы в цепи синусоидального тока. Реальный индуктивный элемент.
ВТД реального
индуктивного элемента
В реальном индуктивном элементе разность фаз между током и напряжением всегда больше 0 и меньше 900.
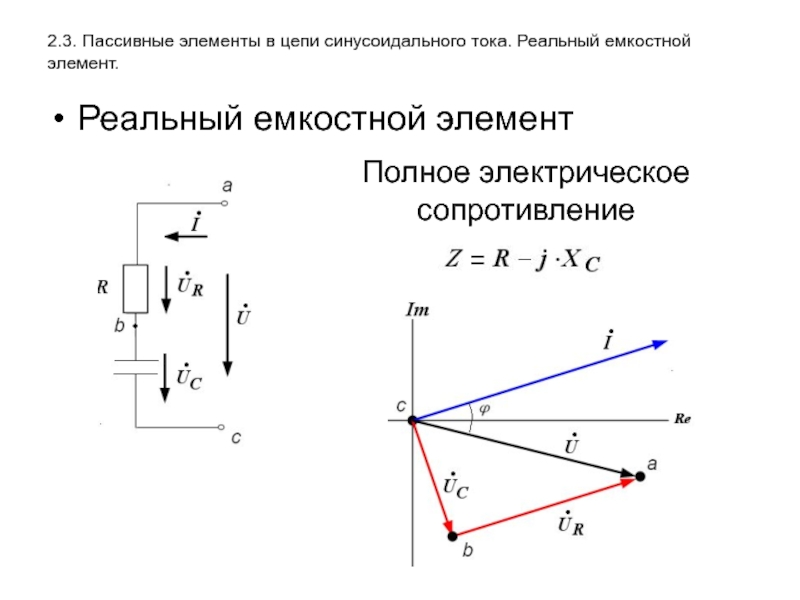
Слайд 202.3. Пассивные элементы в цепи синусоидального тока. Реальный емкостной элемент.
Реальный емкостной
элемент
Полное электрическое сопротивление
Слайд 212.4. Основные законы в цепях переменного тока
Закон Ома:
Резистор
Индуктивность
Емкость
Законы Кирхгофа:
В узле
В
замкнутом контуре
Слайд 222.4. Основные законы в цепях переменного тока
В комплексной форме
Закон Ома:
Законы
Кирхгофа:
В узле
В замкнутом контуре
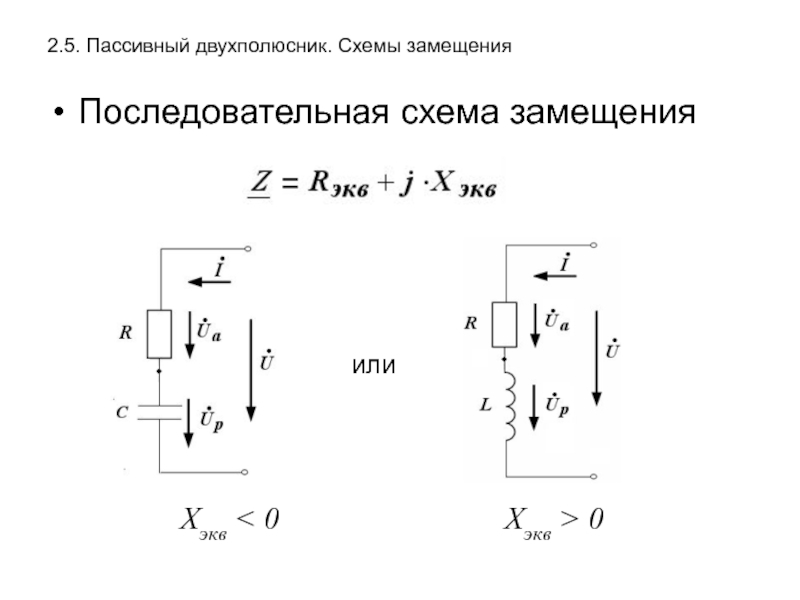
Слайд 252.5. Пассивный двухполюсник. Схемы замещения
Последовательная схема замещения
или
Xэкв < 0
Xэкв > 0
Слайд 272.5. Пассивный двухполюсник. Схемы замещения
Формулы перехода от последовательной к параллельной схеме
замещения
Слайд 312.7. Резонанс напряжений
Режим, при котором в цепи с последовательным соединением R,
L, C элементов ток совпадает по фазе с напряжением называется резонансом напряжений.
Резонанс напряжений возникает, когда
Резонанс напряжений возникает, когда
Слайд 322.7. Резонанс напряжений
Признаки резонанса напряжений:
1. Zэкв = R – минимально возможное;
2.
Ток в цепи максимален;
3. Напряжения катушки и конденсатора равны по модулю и находятся в противофазе;
4. Резонансная частота равна
5. Мощность в цепи чисто активная и максимально возможная;
6. Коэффициент мощности цепи максимален и равен 1.
Слайд 342.8. Резонанс токов
Резонансом тока называют режим, при котором в цепи с
параллельным соединением L и C элементов ток в неразветвленной части цепи совпадает по фазе с напряжением.
Условие резонанса токов
Условие резонанса токов
Слайд 352.8. Резонанс токов
Признаки резонанса токов
1. Yэкв = G – минимально возможное
(сопротивление максимально);
2. Ток в неразветвленной части цепи минимален;
3. Реактивные составляющие токов ветвей равны и находятся в противофазе
6. Коэффициент мощности цепи максимален и равен 1.
4. Мощность, выделяющаяся в цепи чисто активная.
Слайд 362.9. Измерения в цепи переменного тока
Измерение напряжения
Действующее значение – вольтметром
Мгновенное значение
– осциллографом
2. Измерения тока
Действующее значение – амперметром
Мгновенное значение – осциллографом, предварительно преобразовав ток в напряжение
2. Измерения тока
Действующее значение – амперметром
Мгновенное значение – осциллографом, предварительно преобразовав ток в напряжение
Слайд 372.9. Измерения в цепи переменного тока
3. Измерение мощности
Активной мощности – ваттметром
Полной
– с помощью амперметра и вольтметра
Реактивной – куметром, либо с помощью амперметра, вольтметра и ваттметра
Реактивной – куметром, либо с помощью амперметра, вольтметра и ваттметра
Слайд 382.9. Измерения в цепи переменного тока
4. Измерение параметров пассивного двухполюсника
Методом амперметра,
вольтметра, ваттметра
Резонансным методом
Резонансным методом
