- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Фалеса.Трапеция. презентация
Содержание
- 1. Теорема Фалеса.Трапеция.
- 2. Задача Точки М и N середины сторон
- 3. Задача Медианы АМ1 и ВМ2 треугольника АВС
- 4. Задача Параллельные прямые a и b пересекают
- 5. Трапеция Определение. Трапецией называется четырехугольник, две противоположные
- 6. Трапеция. Основные элементы Параллельные стороны называются основаниями
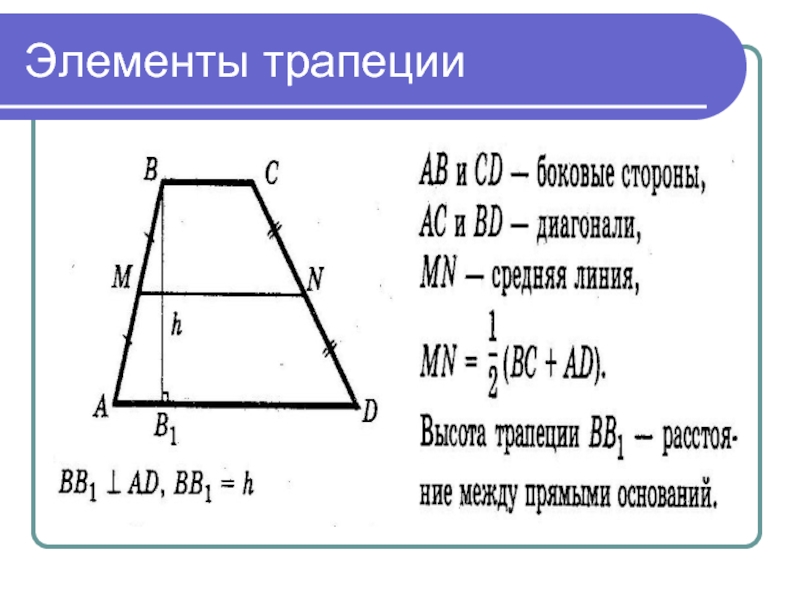
- 7. Элементы трапеции
- 8. Свойства трапеции. 1. Середины оснований, точка пересечения
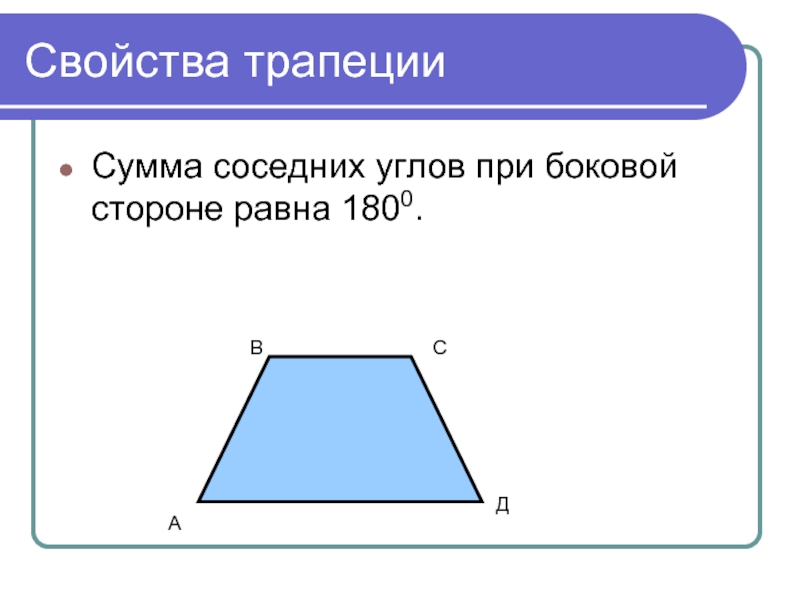
- 9. Свойства трапеции Сумма соседних углов при боковой стороне равна 1800. А С В Д
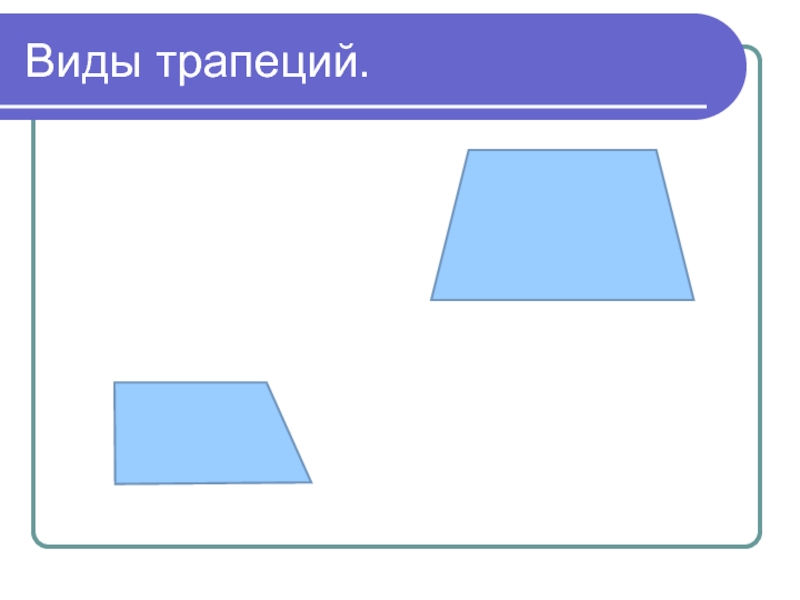
- 10. Виды трапеций.
- 11. Равнобокая трапеция. Определение. Равнобокой (равнобедренной) трапецией называется
- 12. Свойства равнобокой трапеции Диагонали равнобокой трапеции равны.
- 13. Свойства равнобокой трапеции В равнобокой трапеции высота,
- 14. Свойства равнобокой трапеции В равнобокой трапеции прямая,
- 15. Задача. Два угла трапеции равны 320 и 1430. Найти два других ее угла.
- 16. Задача Существует ли трапеция, у которой два противоположных угла острые? Если ответ положительный, сделайте рисунок.
- 17. Задача. Существует ли трапеция, у которой два
- 18. Задача Диагональ трапеции перпендикулярна боковой стороне, а
- 19. Задача Меньшее основание равнобедренной трапеции равно боковой
Слайд 2Задача
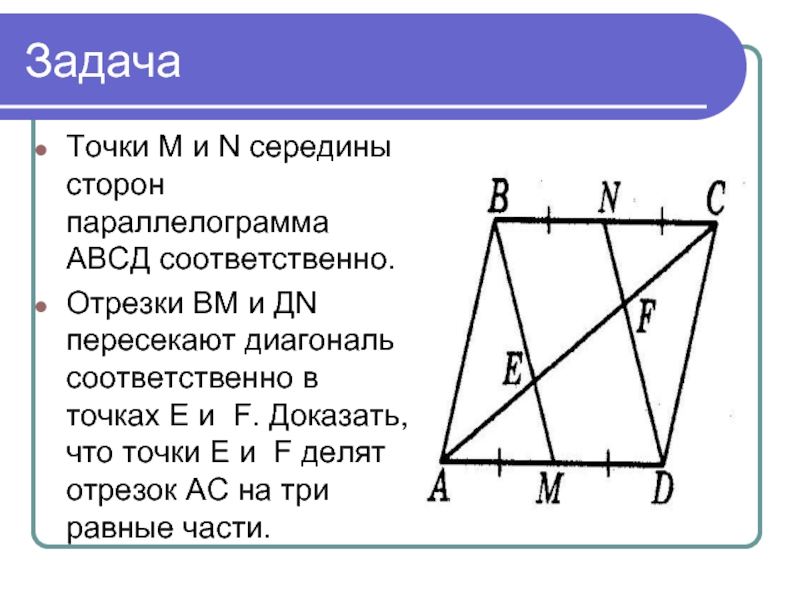
Точки М и N середины сторон параллелограмма АВСД соответственно.
Отрезки ВМ и
ДN пересекают диагональ соответственно в точках Е и F. Доказать, что точки Е и F делят отрезок АС на три равные части.
Слайд 3Задача
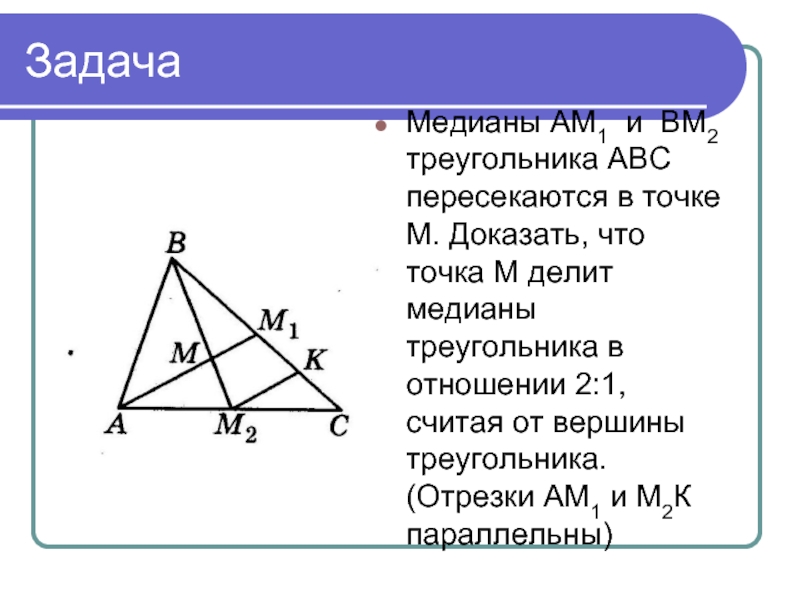
Медианы АМ1 и ВМ2 треугольника АВС пересекаются в точке М. Доказать,
что точка М делит медианы треугольника в отношении 2:1, считая от вершины треугольника. (Отрезки АМ1 и М2К параллельны)
Слайд 4Задача
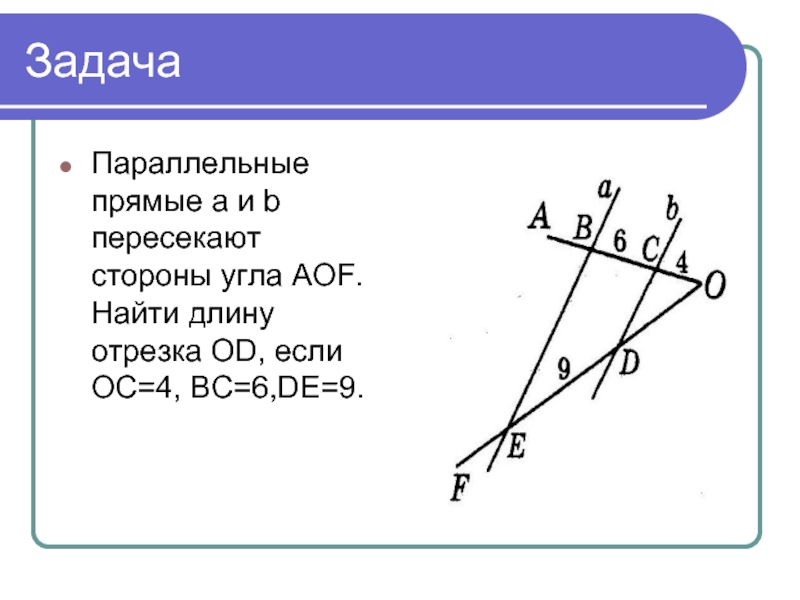
Параллельные прямые a и b пересекают стороны угла AOF. Найти длину
отрезка OD, если OC=4, BC=6,DE=9.
Слайд 5Трапеция
Определение.
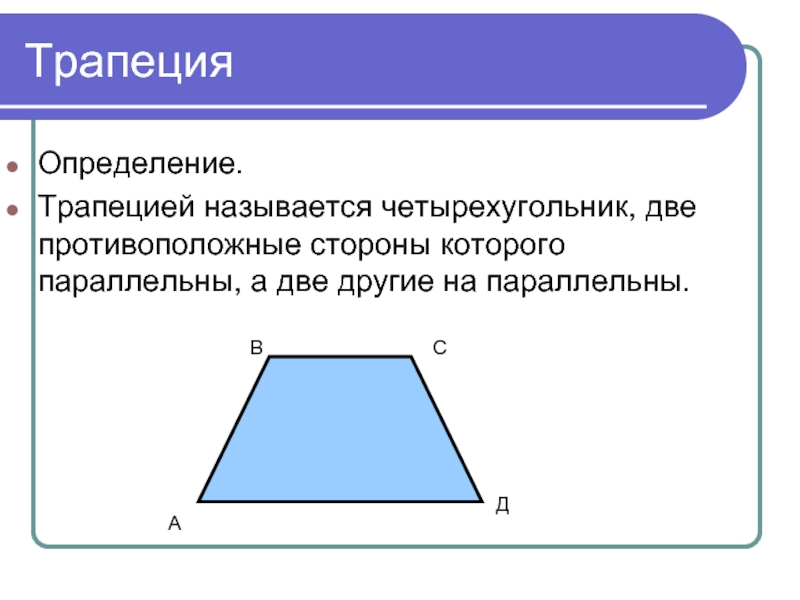
Трапецией называется четырехугольник, две противоположные стороны которого параллельны, а две другие
на параллельны.
А
С
В
Д
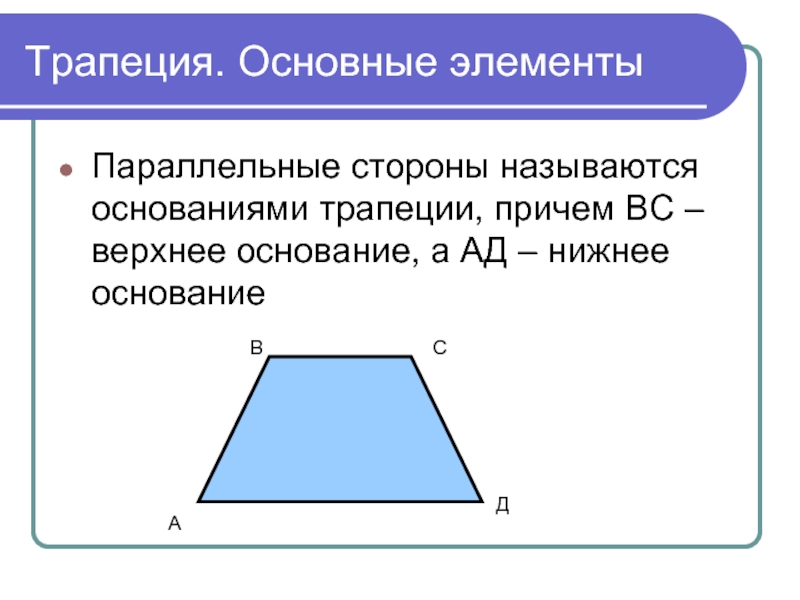
Слайд 6Трапеция. Основные элементы
Параллельные стороны называются основаниями трапеции, причем ВС – верхнее
основание, а АД – нижнее основание
А
С
В
Д
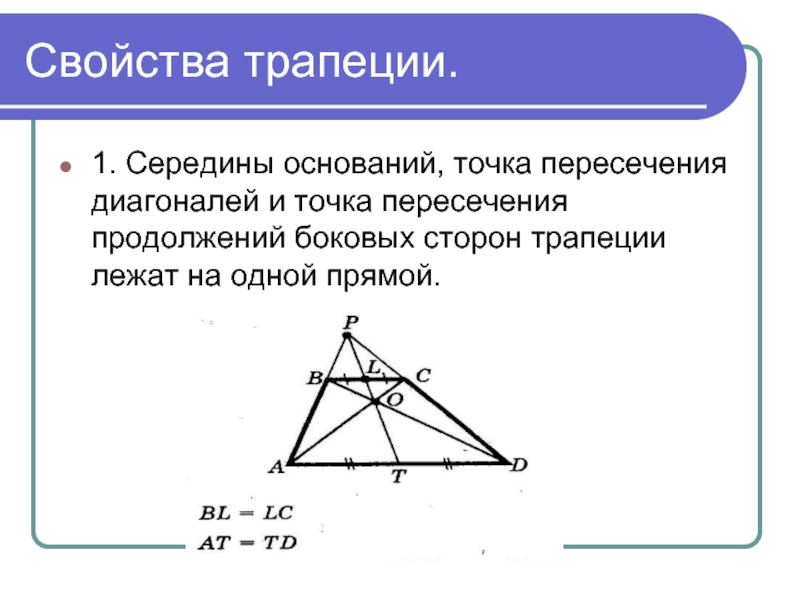
Слайд 8Свойства трапеции.
1. Середины оснований, точка пересечения диагоналей и точка пересечения продолжений
боковых сторон трапеции лежат на одной прямой.
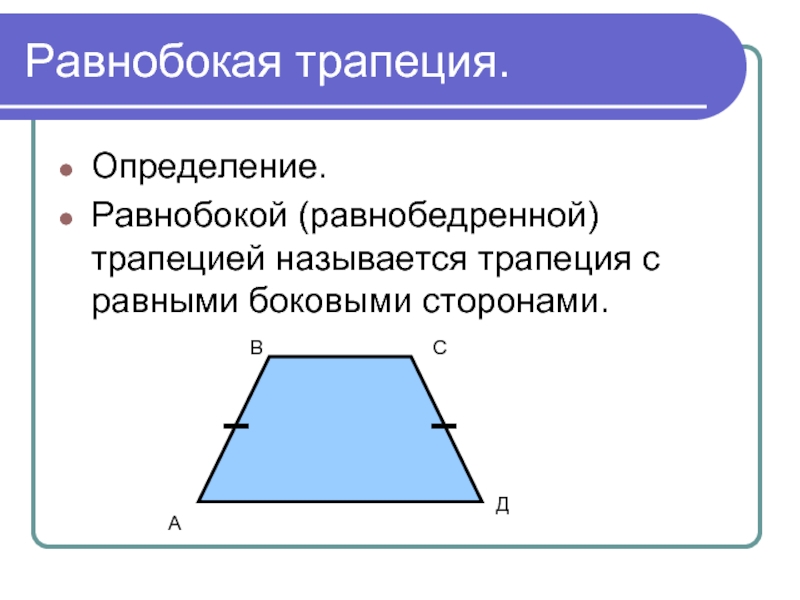
Слайд 11Равнобокая трапеция.
Определение.
Равнобокой (равнобедренной) трапецией называется трапеция с равными боковыми сторонами.
А
С
В
Д
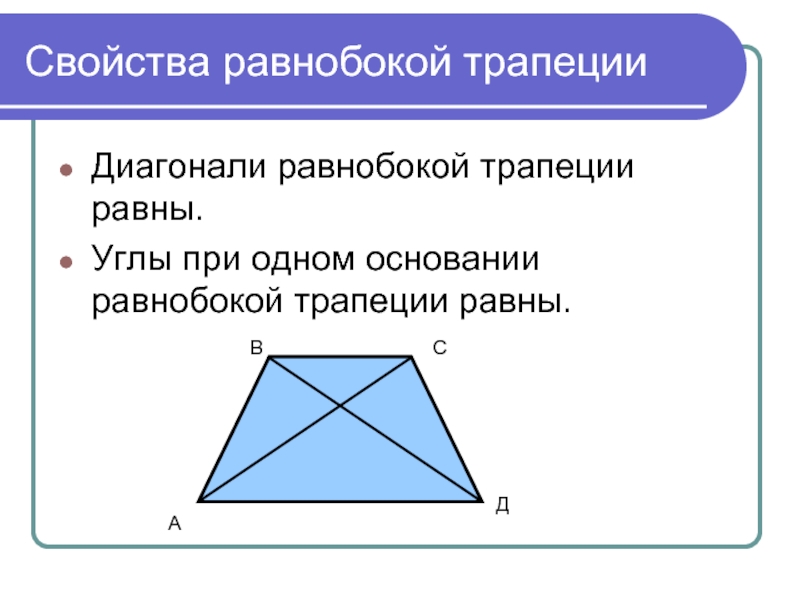
Слайд 12Свойства равнобокой трапеции
Диагонали равнобокой трапеции равны.
Углы при одном основании равнобокой трапеции
равны.
А
С
В
Д
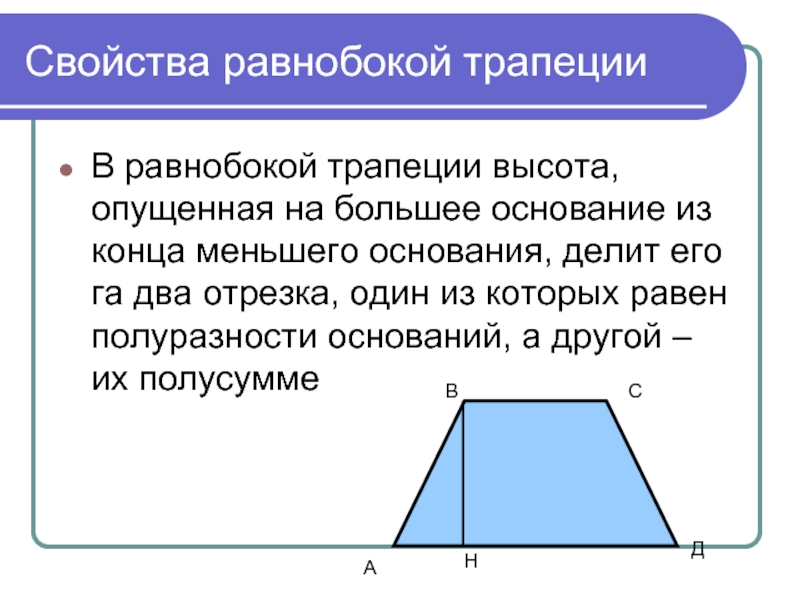
Слайд 13Свойства равнобокой трапеции
В равнобокой трапеции высота, опущенная на большее основание из
конца меньшего основания, делит его га два отрезка, один из которых равен полуразности оснований, а другой – их полусумме
А
С
В
Д
Н
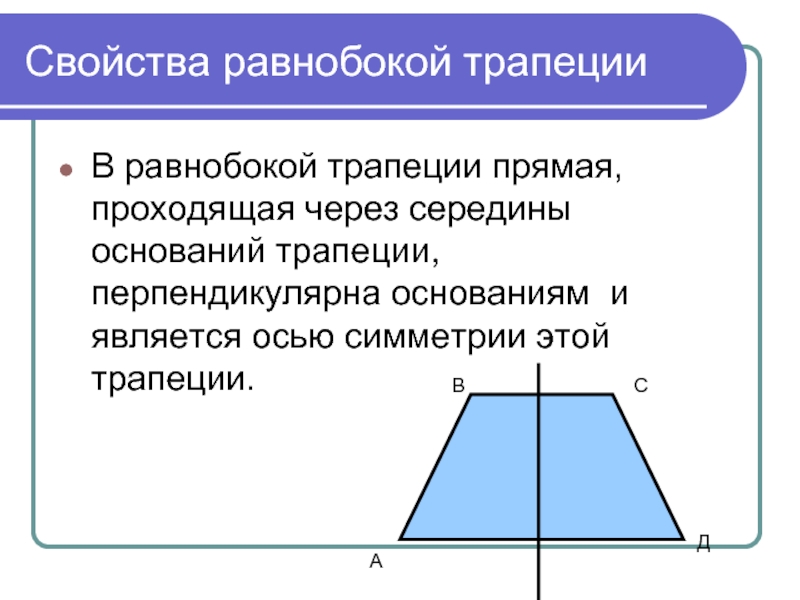
Слайд 14Свойства равнобокой трапеции
В равнобокой трапеции прямая, проходящая через середины оснований трапеции,
перпендикулярна основаниям и является осью симметрии этой трапеции.
А
С
В
Д
Слайд 16Задача
Существует ли трапеция, у которой два противоположных угла острые?
Если ответ положительный,
сделайте рисунок.
Слайд 17Задача.
Существует ли трапеция, у которой два противоположных угла равны?
Если ответ положительный,
сделайте рисунок.
Слайд 18Задача
Диагональ трапеции перпендикулярна боковой стороне, а острый угол, лежащий против этой
диагонали, равен 520. Найти другие углы трапеции, если ее меньшее основание равно второй боковой стороне.
Слайд 19Задача
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагонали перпендикулярны боковым
сторонам. Найти углы трапеции.