- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приближённые вычисления интегралов презентация
Содержание
- 1. Приближённые вычисления интегралов
- 2. Цель урока: Научить вычислять определённые интегралы с
- 3. План урока Приближённый метод вычисления определённого интеграла.
- 4. Ход урока: Приближённый метод вычисления определённого интеграла.
- 5. В процессе решения задачи повторить схему вычисления
- 6. Итак, решая поставленную задачу получили, что
- 7. рис. 1 рис. 2 Для
- 8. Для приближённого вычисления интеграла можно использовать
- 9. Рассмотрим рис. 2. Объединение
- 10. Точность вычисления зависит от выбора п
- 11. Если /(х) бывает, то поменять местами
- 12. Пример. На сколько частей надо разбить отрезок [1;2], чтобы вычислить Решение.
- 13. 2 Составление программы для вычисления
Слайд 1Приближённые вычисления интегралов
интегрированный урок
алгебры и информатики
Учителя : Мещерина В.В.и Волков
Слайд 2Цель урока:
Научить вычислять определённые интегралы с помощью ПЭВМ в случае, когда
Слайд 3План урока
Приближённый метод вычисления определённого интеграла. Формула трапеции.
Составление программы для вычисления
Отчёт по программе.
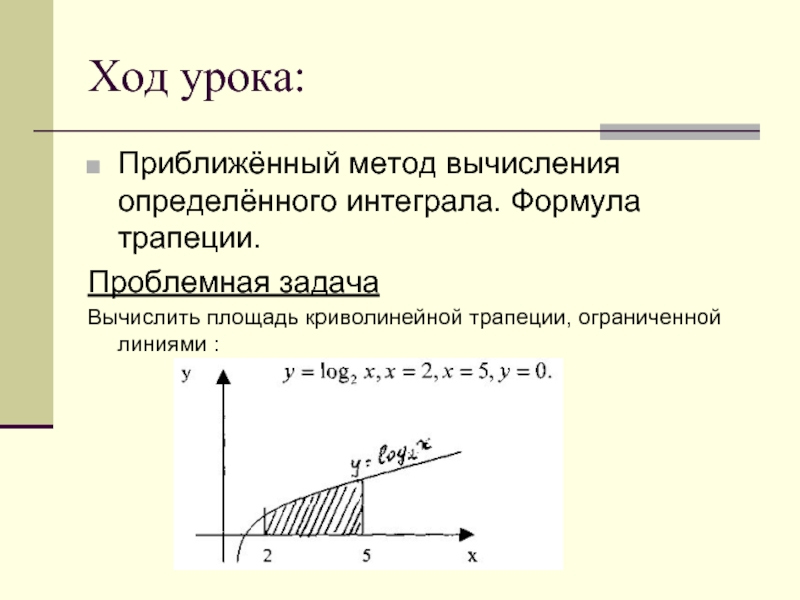
Слайд 4Ход урока:
Приближённый метод вычисления определённого интеграла. Формула трапеции.
Проблемная задача
Вычислить площадь криволинейной
Слайд 5В процессе решения задачи повторить схему вычисления площади фигуры, ограниченной графиками
Построить графики функций
Найти абсциссы X1 и Х2 точек пересечения этих графиков.
Если точек пересечения две, то определить, график какой из функций на отрезке [х1, х2] расположен выше.
Найти площадь фигуры по формуле
Если точек пересечения больше двух, то разбить фигуру на части.
Слайд 6Итак, решая поставленную задачу получили, что
Возникла ситуация, когда первообразная для
для нахождения значения
применяют приближенные методы.
Рассмотрим один из них .
Для простоты будем считать функцию неотрицательной и непрерывной на
[а,в].
Слайд 7
рис. 1 рис. 2
Для вычисления площади данной фигуры [а, Ь] разбивается
на п частей и на каждом участке строят
прямоугольники с высотами
Слайд 8Для приближённого вычисления интеграла можно использовать формулу
(1).
Для приближённого вычисления интеграла
(1).
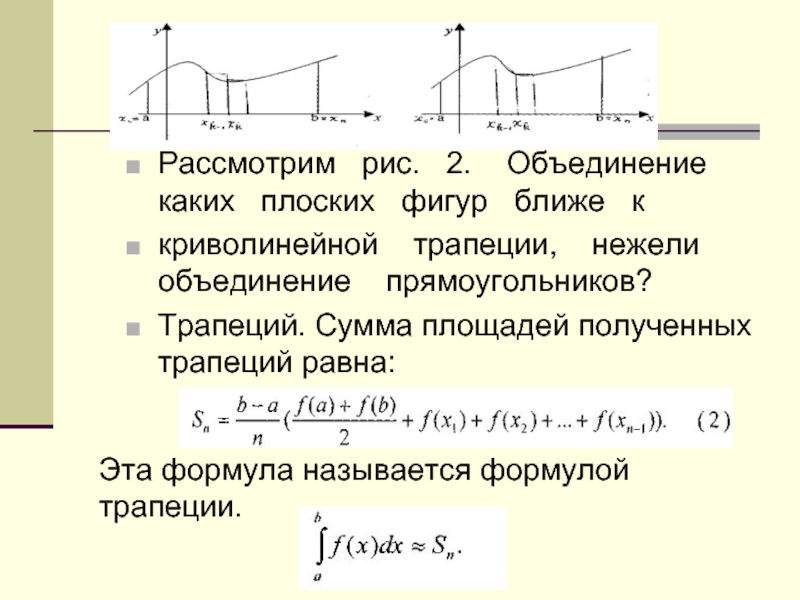
Слайд 9Рассмотрим рис. 2. Объединение каких плоских
криволинейной трапеции, нежели объединение прямоугольников?
Трапеций. Сумма площадей полученных трапеций равна:
Эта формула называется формулой трапеции.
Слайд 10
Точность вычисления зависит от выбора п , чем больше п, тем
Существует несколько способов оценки числа п. Один из них основывается на разности оценок интеграла снизу и сверху.
Слайд 11Если /(х) бывает, то поменять местами нижний и верхний пределы
Если /(х) бывает, то поменять местами нижний и верхний пределы интегрирования. Это следует из того, что:
Слайд 132 Составление программы для вычисления площади криволинейной
Каждый учащийся получает индивидуальное задание. Выполняет его,
используя компьютер. Отчёт по программе принимает учитель
информатики.





![рис. 1 рис. 2 Для вычисления площади данной фигуры [а, Ь] разбивается точками на п частей](/img/tmb/3/234523/d904c4e527e8e5d467efe81396d738b4-800x.jpg)



![Пример. На сколько частей надо разбить отрезок [1;2], чтобы вычислитьРешение.](/img/tmb/3/234523/79c613e1b63d2542e8e65667ab434cae-800x.jpg)






