- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подобные треугольники презентация
Содержание
- 1. Подобные треугольники
- 2. Содержание
- 3. Пропорциональные отрезки
- 4. Подобные фигуры
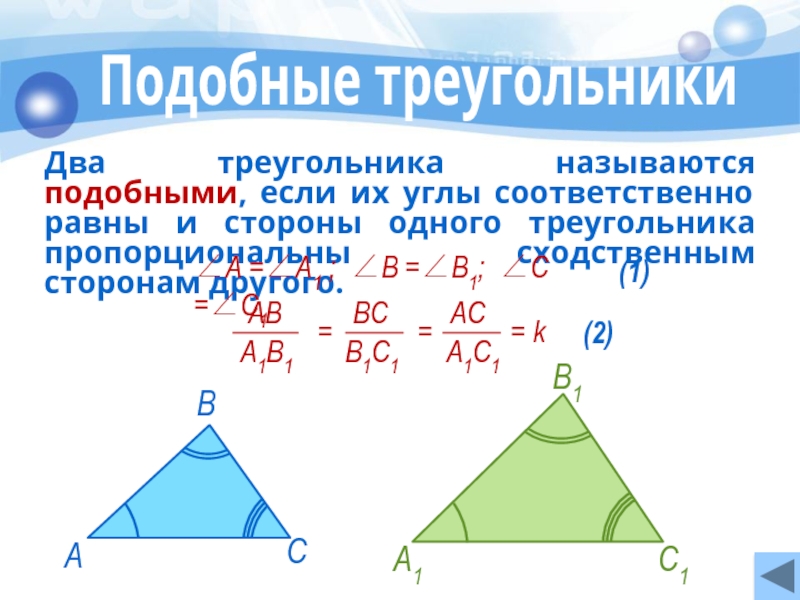
- 5. Подобные треугольники Два треугольника называются подобными, если
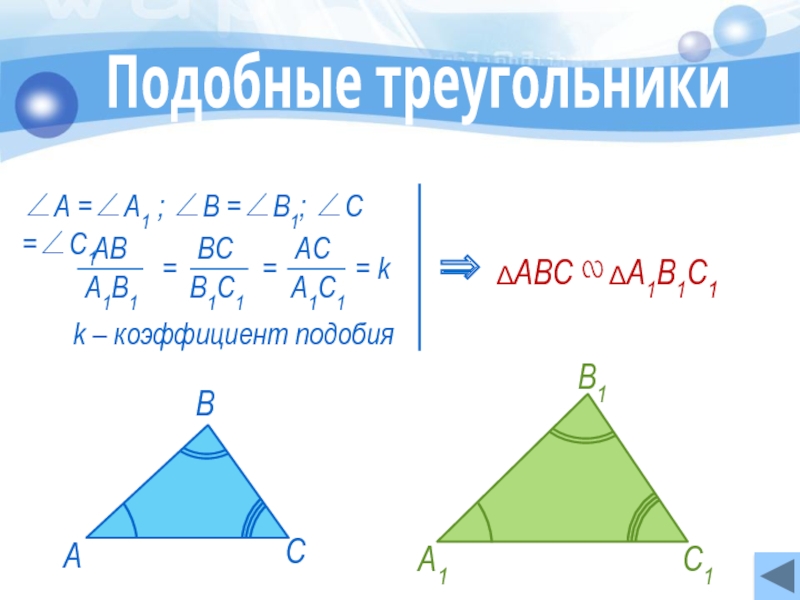
- 6. k – коэффициент подобия ∠А =∠А1 ;
- 7. Т.к. ∠А =∠А1 , то по теореме
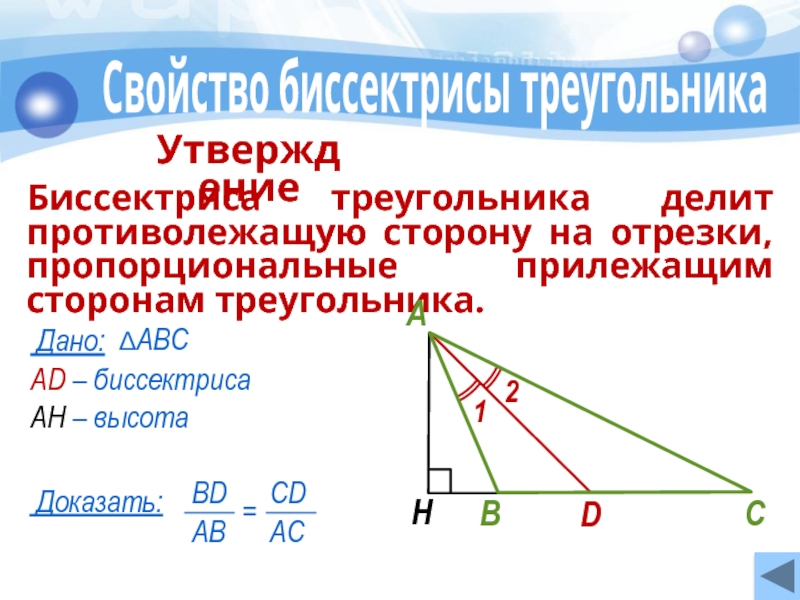
- 8. AD – биссектриса АН – высота
- 9. Т.к. ∆АВD и ∆АСD имеют общую высоту
- 10. Самостоятельная работа
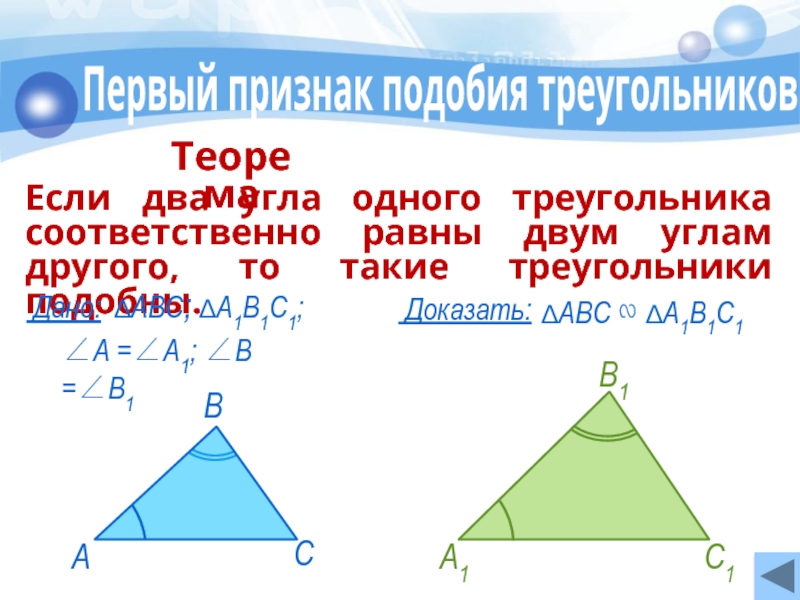
- 11. Первый признак подобия треугольников Если два
- 12. Первый признак подобия треугольников Доказательство:
- 13. Второй признак подобия треугольников Если две
- 14. Третий признак подобия треугольников Если три
Слайд 1Подобные треугольники
Автор: Семенова Елена Юрьевна
МОУ СОШ № 5 – «Школа здоровья
Слайд 5Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны и
∠А =∠А1 ; ∠В =∠В1; ∠С =∠С1
(1)
(2)
Слайд 7Т.к. ∠А =∠А1 , то по теореме об
k – коэффициент подобия
∆АВС
⇒
Отношение площадей подобных треугольников
Дано:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Теорема
Доказать:
Доказательство:
отношении площадей треугольников
По формуле (2)
Слайд 8AD – биссектриса
АН – высота
∆АВС
Свойство биссектрисы треугольника
Дано:
Биссектриса
Утверждение
Доказать:
Н
D
1
2
Слайд 9Т.к. ∆АВD и ∆АСD имеют общую высоту
⇒
Свойство биссектрисы треугольника
углы (∠1 =∠2), поэтому
Из равенств (1) и (2) получаем
С другой стороны, эти же треугольники имеют равные
Ч.т.д.
Слайд 11Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны
Теорема
∆АВС ∾ ∆А1В1С1
Дано:
Доказать:
∠А =∠А1; ∠В =∠В1
∆АВС; ∆А1В1С1;
Слайд 12Первый признак подобия треугольников
Доказательство:
По теореме о сумме углов
Тогда по теореме об отношении площадей треугольников
С = 180° ‒ (∠А +∠В)
С1 = 180° ‒ (∠А1 +∠В1)
⇒ ∠С =∠С1
Таким образом, ∠А =∠А1 ; ∠В =∠В1; ∠С =∠С1.
из
⇒
Ч.т.д.
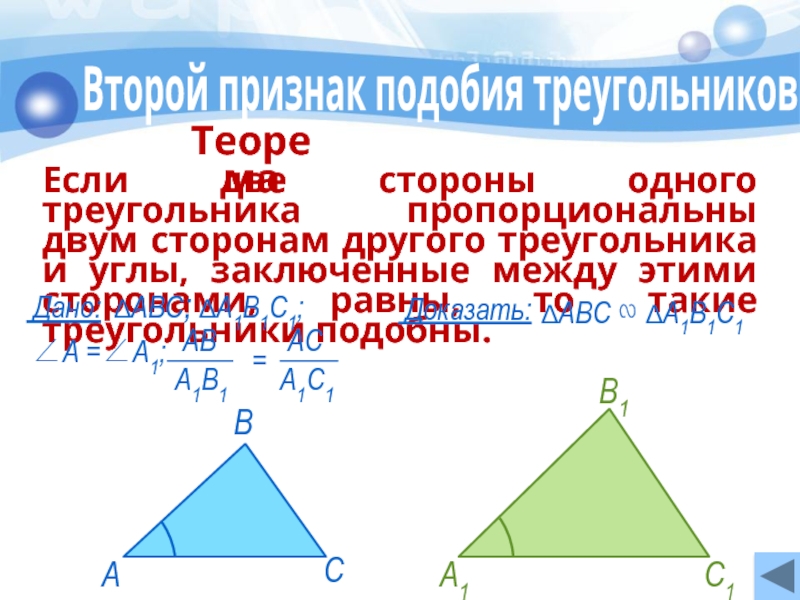
Слайд 13Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум
Теорема
∆АВС ∾ ∆А1В1С1
Дано:
Доказать:
∠А =∠А1;
∆АВС; ∆А1В1С1;
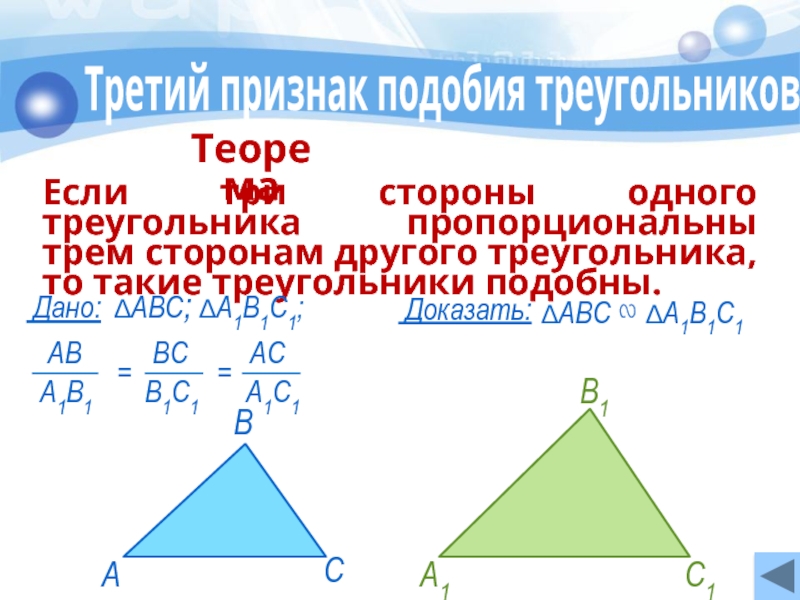
Слайд 14Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем
Теорема
∆АВС ∾ ∆А1В1С1
Дано:
Доказать:
∆АВС; ∆А1В1С1;