- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Особливості обробки й інтерпретації результатів дослідних робіт в умовах тріщиннокарстових водоносних горизонтів (частина 1) презентация
Содержание
- 1. Особливості обробки й інтерпретації результатів дослідних робіт в умовах тріщиннокарстових водоносних горизонтів (частина 1)
- 2. Розглядаються питання: Поняття про тріщинуватість та закарстованість
- 3. Тріщинуватість Тріщинуватість -
- 4. Види тріщинуватості Нетектонічна тріщинуватість гірських порід -
- 5. Наслідки явища тріщинуватості Позитивні
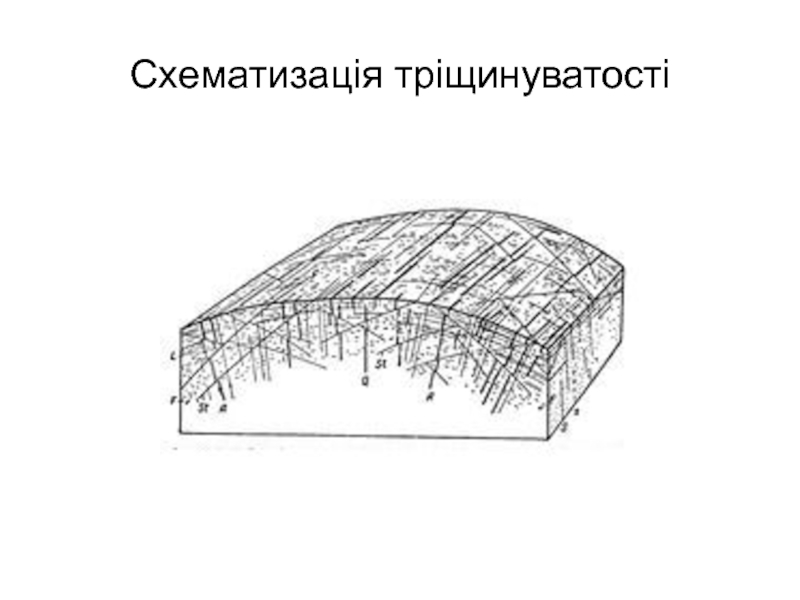
- 6. Схематизація тріщинуватості
- 7. Карст та закарстованість Карст — геологічна формація,
- 8. Схематизація закарстованості
- 9. Загальна характеристика Тріщинуваті
- 10. “Своєрідна пористість” Тріщинуватість розглядається, як «своєрідна
- 11. “Подвійна” природа пустот
- 12. “Подвійна” природа пустот Проникні блоки
- 13. Роль карстових порожнин Роль крупних карстових порожнин
- 14. ОСОБЛИВОСТІ ПРОЦЕСУ ФІЛЬТРАЦІЇ РІДИНИ В ТРІЩИНУВАТИХ ПОРОДАХ
- 15. Основні положення про рух рідини в тріщинуватій
- 16. Чисто тріщинувата порода, у якої блоки є
- 17. Структура фільтраційного потоку в тріщинуватих породах
- 18. “Перерозподіл” напорів При різкій зміні напору в
- 19. Напрямки вивчення процесів фільтрації в тріщинуватих породах
- 20. Застосування теорії нестаціонарної фільтрації рідини в тріщинувато-пористій
- 21. Схеми гетерогенної структури гірської породи
- 22. Математична модель При прийнятих передумовах
- 23. Математична модель α − безрозмірний коефіцієнт, що
- 24. Математична модель Як правило, n1 K2, то
- 25. Математична модель
- 26. Висновок по математичній моделі (наближення результатів)
- 28. Підходи до визначення геофільтраційних параметрів Визначення
- 29. Недоліки першого підходу Складність визначення параметрів диференційних
- 30. Типовий графік простеження за часом в тріщинно-карстовому
- 31. Коротка характеристика ділянок графіка S –
- 32. Приклад визначення геофільтраційних параметрів із застосуванням методу
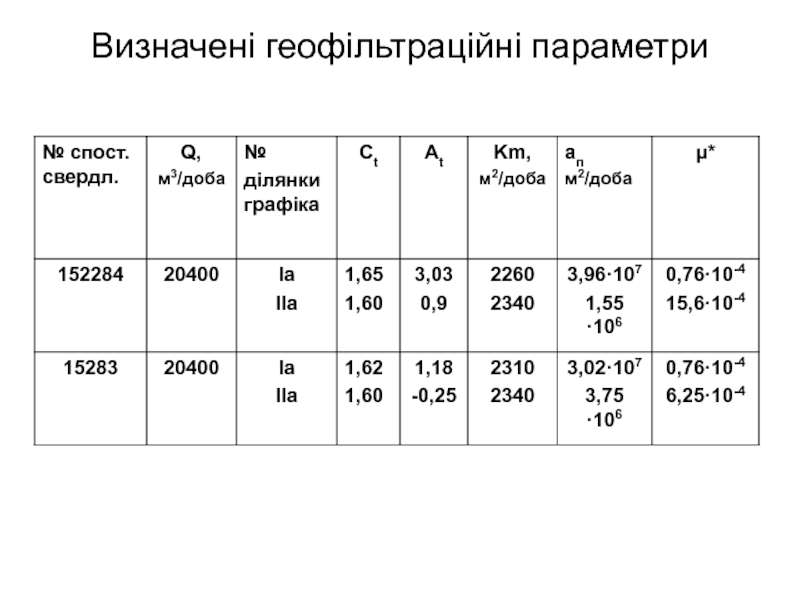
- 34. Визначені геофільтраційні параметри
- 35. Інтерпретація результатів Параметри шару,
- 37. ОСОБЛИВОСТІ ОБРОБКИ Й ІНТЕРПРЕТАЦІЇ РЕЗУЛЬТАТІВ ДОСЛІДНИХ РОБІТ
- 38. Розглядаються питання: Особливості інтерпретації результатів дослідних робіт
- 39. Автомодельна функція Шляхом моделювання на ЕОМ
- 40. Параметри “автомодельної функції” Автомодельна
- 42. Зона “надпровідності” Аналіз графіку, показує, що в
- 43. Приклади та “залежності” Встановлено, що при невеликій
- 44. Приклади та “залежності” Незважаючи на те, що
- 45. Приклади та “залежності” Характерною рисою шарів з
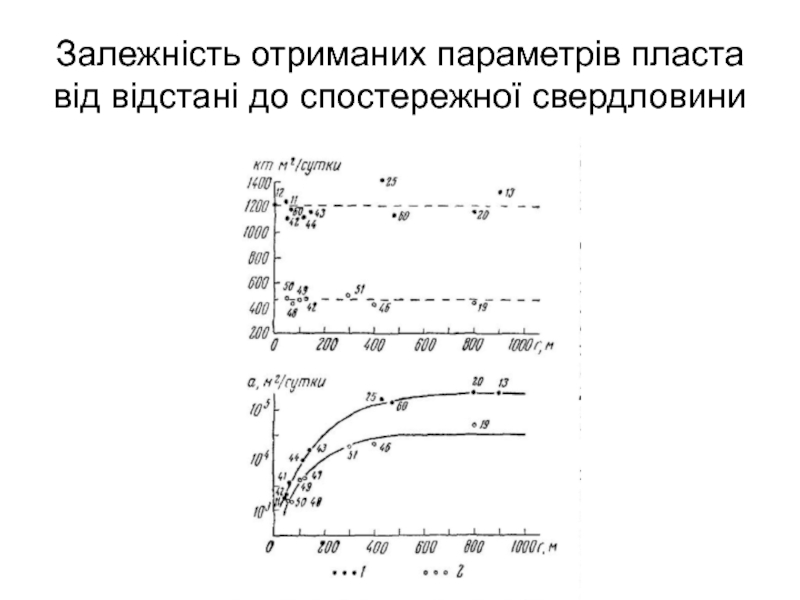
- 46. Залежність отриманих параметрів пласта від відстані до спостережної свердловини
- 47. Приклади та “залежності” На графіку добре видно,
- 48. Складність інтерпретації результатів При вирішенні питання про
- 49. Складність інтерпретації результатів графіків часового простеження
- 50. Приклади та “залежності” Роль комбінованого простеження
- 51. Приклади та “залежності” (Майкайнарська ділянка)
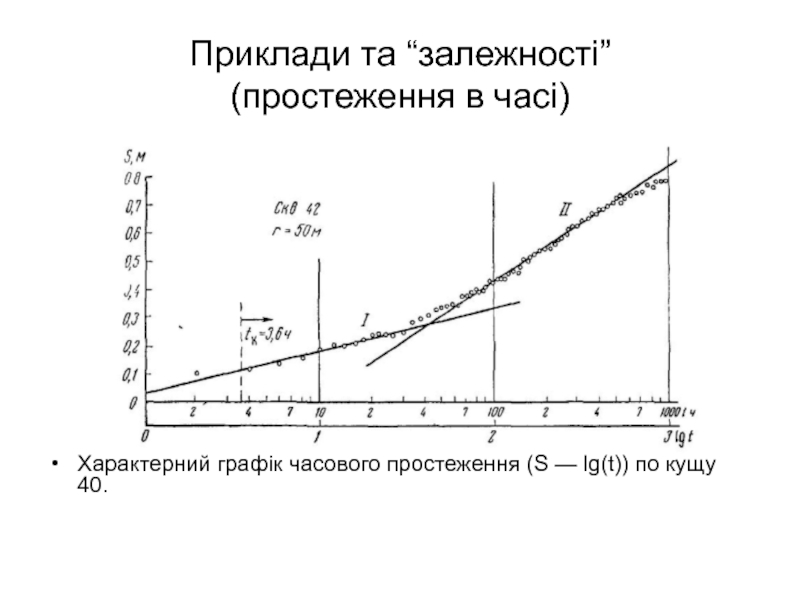
- 52. Приклади та “залежності” (простеження в часі)
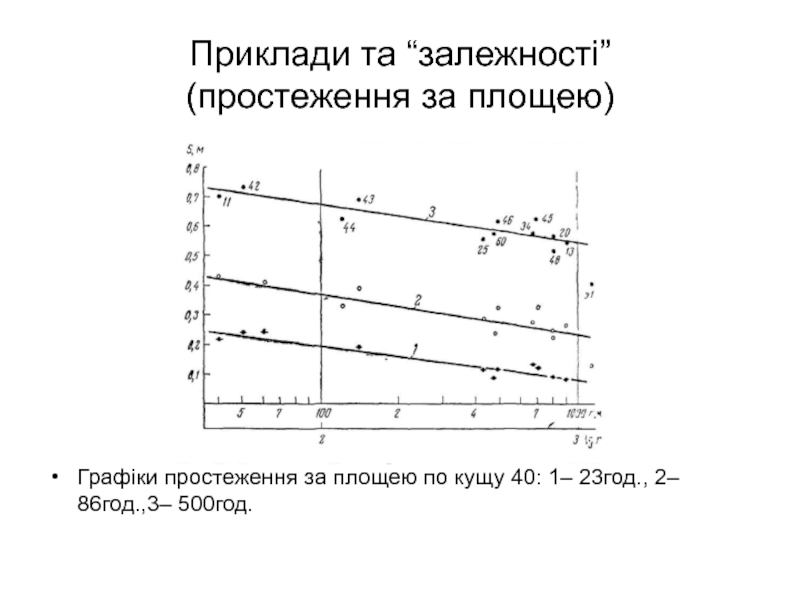
- 53. Приклади та “залежності” (простеження за площею)
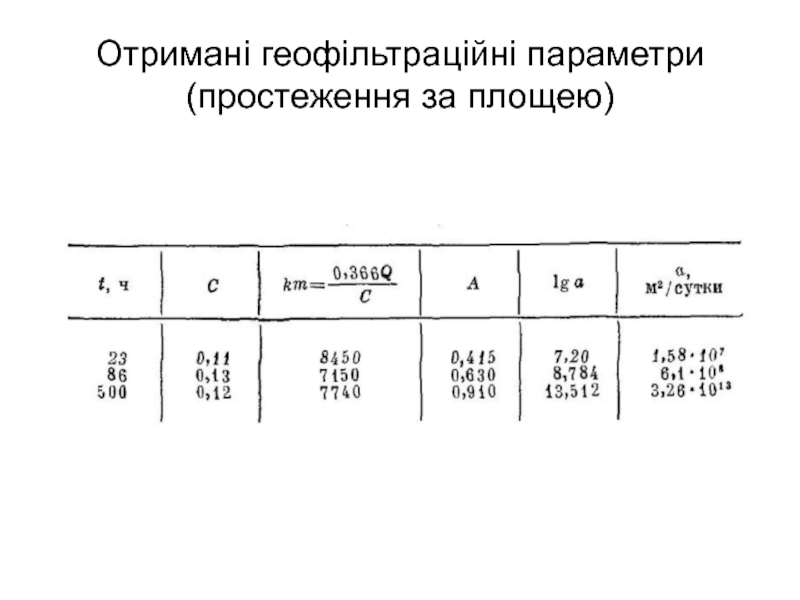
- 54. Отримані геофільтраційні параметри (простеження за площею)
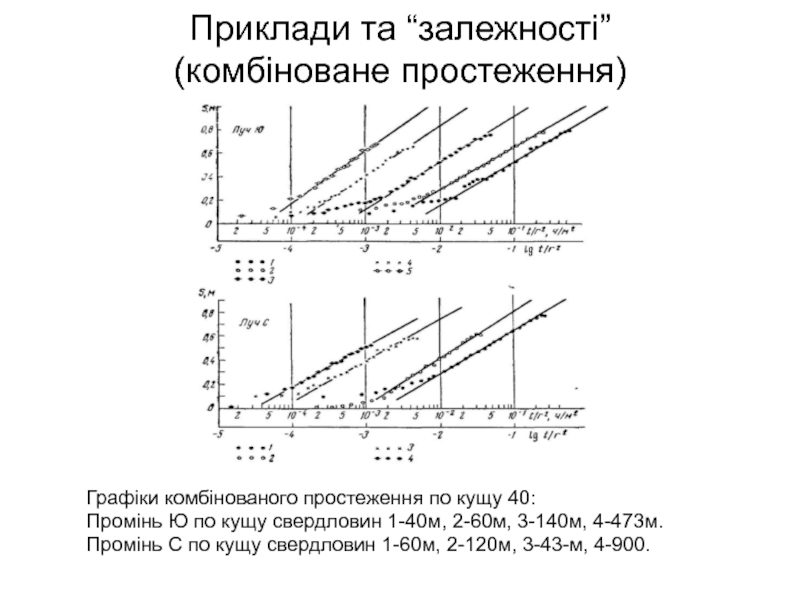
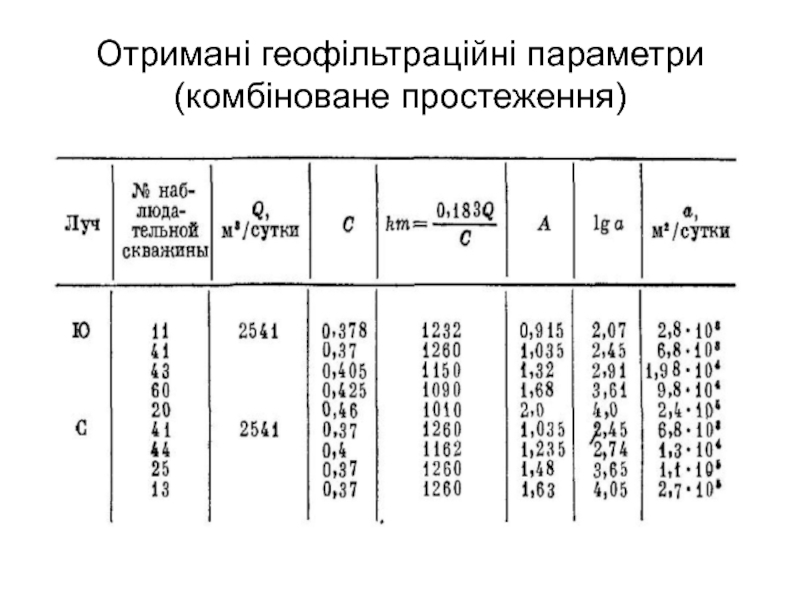
- 55. Приклади та “залежності” (комбіноване простеження)
- 56. Отримані геофільтраційні параметри (комбіноване простеження)
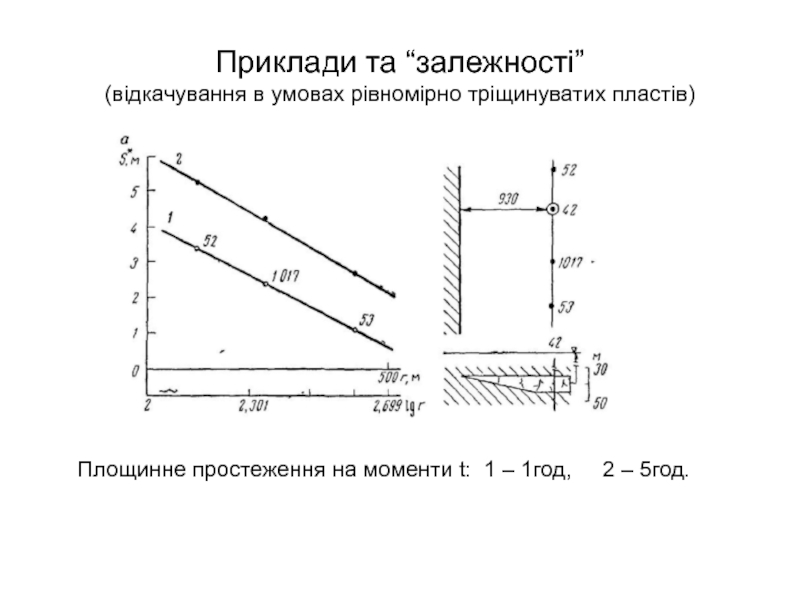
- 57. Приклади та “залежності” (відкачування в умовах рівномірно
- 58. Приклади та “залежності” (відкачування в умовах рівномірно
- 59. Приклади та “залежності” (відкачування в умовах рівномірно
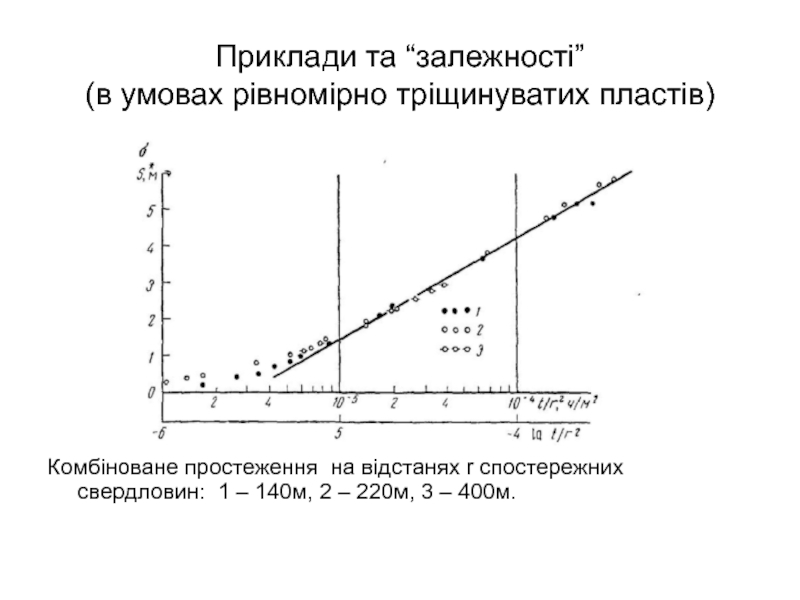
- 60. Приклади та “залежності” (в умовах рівномірно тріщинуватих
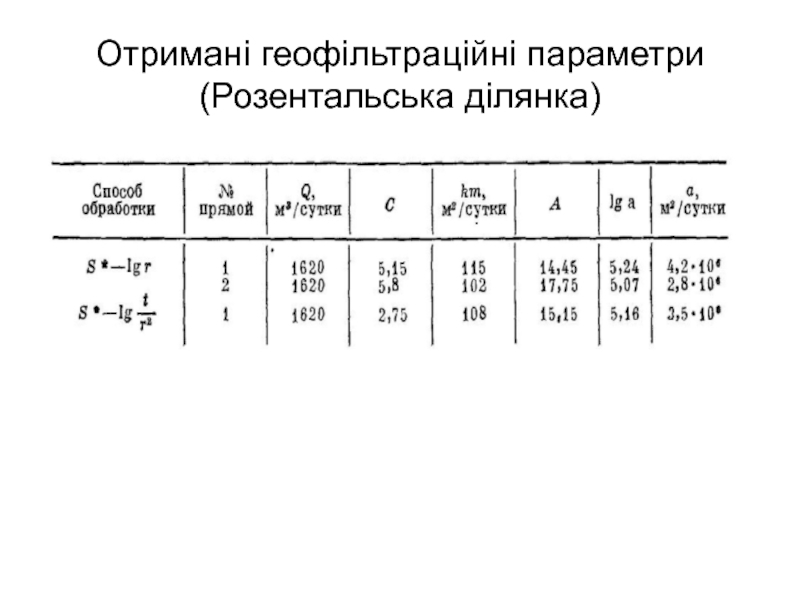
- 61. Отримані геофільтраційні параметри (Розентальська ділянка)
- 62. Приклади та “залежності” (Уральська ділянка)
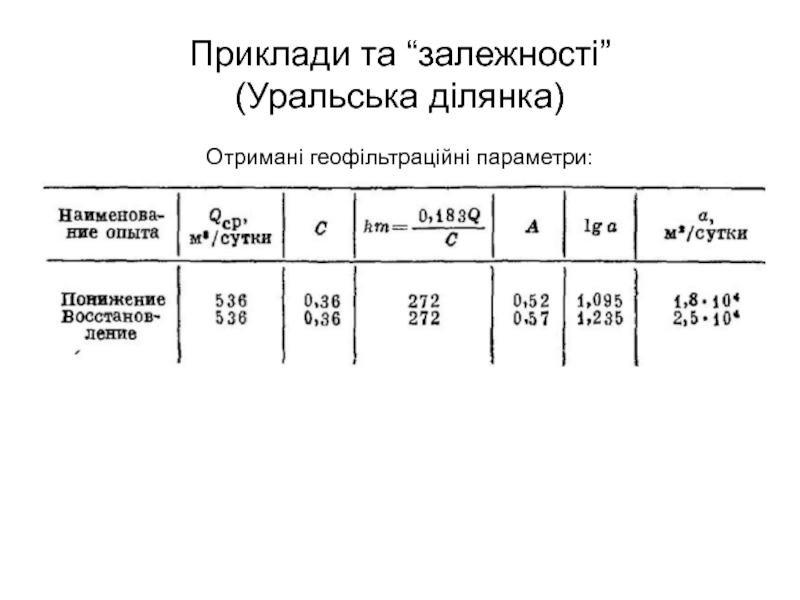
- 63. Приклади та “залежності” (Уральська ділянка) Отримані геофільтраційні параметри:
- 64. Приклади та “залежності” (Уральська ділянка)
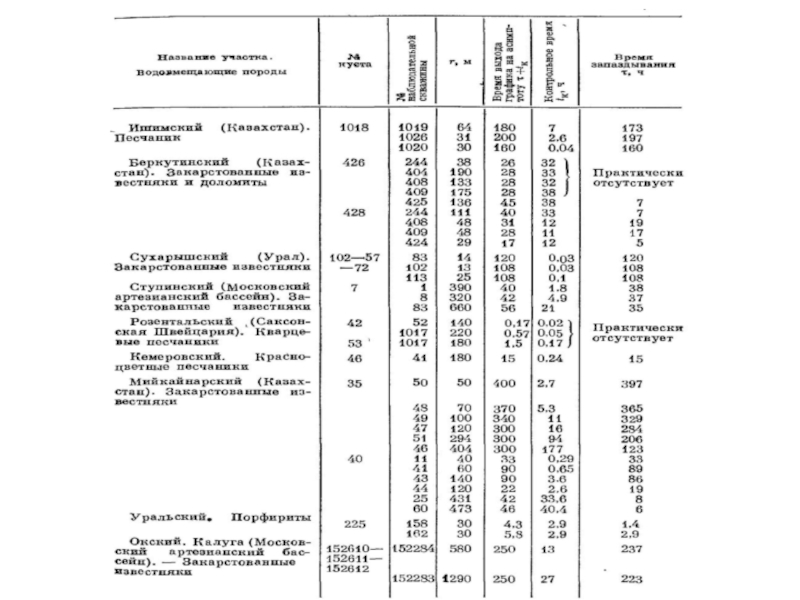
- 65. Час “запізнення”
- 67. Висновки: У тріщинних середовищах, що характеризуються
- 68. Висновки: Асимптотичні ділянки
- 69. Висновки: В умовах сполучення ефекту
- 70. ВОДОНОСНІ ГОРИЗОНТИ У ПОРОДАХ З РІЗКО НЕРІВНОМІРНОЮ ТРІЩИНУВАТІСТЮ
- 71. Загальна характеристика У багатьох випадках, особливо в
- 72. Підхід до розрахунку геофільтраційних параметрів Підхід
- 73. Форми прояву впливу великих тріщин
- 74. Результати дослідних відкачок із сильно метаморфізованих порід
- 75. Результати дослідних відкачок із сильно метаморфізованих архею
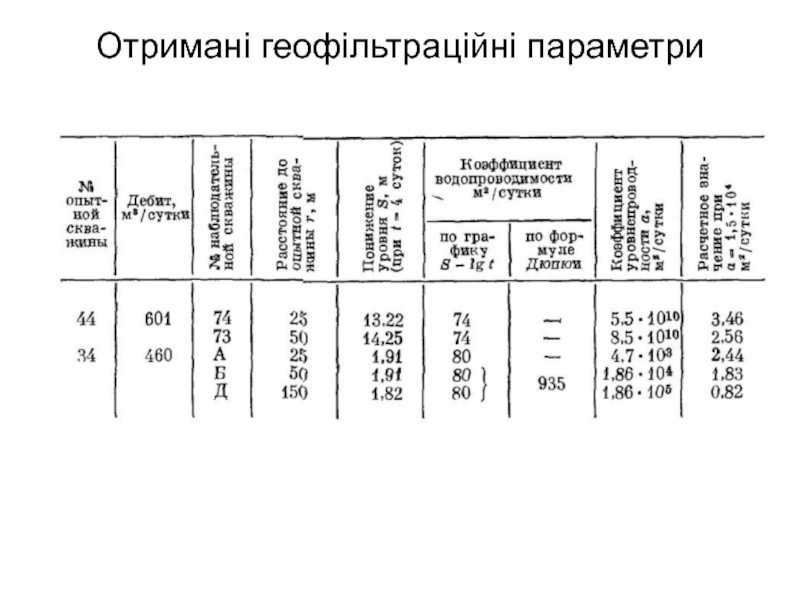
- 76. Отримані геофільтраційні параметри
- 77. Інтерпретація результатів З табл. видно, що при
- 78. Інтерпретація результатів Випадок, коли порушення радіальності потоку
- 79. Інтерпретація результатів У випадках подібних до відкачка
- 80. Висновок Розглянуті в даному розділі умови можна
- 81. ВОДОНОСНІ ГОРИЗОНТИ В АНІЗОТРОПНИХ ТРІЩИНУВАТИХ ПОРОДАХ
- 82. Загальні положення У роботах Е. М. Смехова,
- 83. Метод ізотропної деформації простору
- 84. Метод ізотропної деформації простору
- 85. Метод ізотропної деформації простору Величина зниження рівня
- 86. Для визначення параметрів з використанням всіх
- 88. Загальні висновки 1. Тріщинуваті й закарстовані породи
- 89. Загальні висновки 4. У
Слайд 1ОСОБЛИВОСТІ ОБРОБКИ Й ІНТЕРПРЕТАЦІЇ
РЕЗУЛЬТАТІВ ДОСЛІДНИХ РОБІТ В УМОВАХ
ТРІЩИНУВАТИХ І ТРІЩИННО-КАРСТОВИХ
ВОДОНОСНИХ ГОРИЗОНТІВ
(частина
Слайд 2Розглядаються питання:
Поняття про тріщинуватість та закарстованість гірських порід.
Загальна характеристика та особливості
Особливості процесу фільтрації рідини в тріщинуватих породах.
Водоносні горизонти в тріщинуватих породах.
Приклад визначення геофільтраційних параметрів у водоносних горизонтах тріщинуватих порід.
Слайд 3Тріщинуватість
Тріщинуватість - явище поділу гірських порід земної кори тріщинами різної
Слайд 4Види тріщинуватості
Нетектонічна тріщинуватість гірських порід - наслідок розтріскування гірських порід в
Тектонічна тріщинуватість гірських порід розвивається в зв'язку з напругою, що виникають в гірських породах під впливом глибинних тектонічних сил. Виділяються тріщини відриву і тріщини сколювання, які утворюють системи, закономірно орієнтовані по відношенню до великих тектонічних структур; в зв'язку з розвитком останніх відбувається розтріскування гірських порід.
При планетарній тріщинуватості гірських порід напруги в земній корі виникають під дією планетарних явищ (наприклад, зміни частоти обертання і форми Землі, "твердих припливів" і т.п.).
Слайд 5Наслідки явища тріщинуватості
Позитивні наслідки:
– розсічення
– глибинні горизонти тріщинуватих порід можуть бути колекторами прісної води, нафти і газу.
– тріщинуватість гірських порід забезпечує гарне дроблення гірських порід при відбої гірських порід, що сприяє застосуванню економічних систем розробки з само обваленням руди.
Негативні наслідки:
– зниження стійкості масивів гірських порід. Характеристики міцності масиву тріщинуватих гірських порід підвищують цементацією, силікатизацією, бітумізацією і смоло ін’єкційним зміцненням .
Слайд 7Карст та закарстованість
Карст — геологічна формація, яка формується в процесі розчинення
Карстові явища пов'язані з карбонатними (вапняк, доломіт, крейда, мармур та ін.) та не карбонатними (гіпс, ангідрит) породами.
Слайд 9Загальна характеристика
Тріщинуваті та закарстовані породи, як правило,
істотною неоднорідністю;
анізотропією фільтраційних і ємнісних властивостей;
різним механізмом утворення тріщинуватості та закарстованості;
різною природою пустот у скельних гірських породах.
Слайд 10“Своєрідна пористість”
Тріщинуватість розглядається, як «своєрідна пористість», при якій роль зерен
Макротріщини є, як би, порами першого порядку. У свою чергу блоки породи можуть бути або непроникні, або пористі, кавернозні або розбиті густою сіткою мікротріщин (пори другого порядку).
Слайд 11“Подвійна” природа пустот
Макротріщини (а також окремі тектонічні
Для такого середовища характерна:
підвищена провідність;
низька ємність;
висока п'єзопровідність.
Слайд 12“Подвійна” природа пустот
Проникні блоки з порожнечами другого порядку (мікротріщини).
Для них характерною є:
мала водопровідність;
підвищена ємність;
відносно низька п'єзо провідність.
Ці пустоти визначають переважно ємнісні властивості тріщинуватих порід.
Слайд 13Роль карстових порожнин
Роль крупних карстових порожнин у загальній ємності тріщинно-карстових порід
у загальному обсязі породи.
Так, за даними М. М. Сунцова, обсяг карстових порожнин становить лише 0,3% у загальному обсязі закарстованої породи.
Тому карстові пустоти й порожнини розглядаються
як аналоги великих тріщин.
Слайд 15Основні положення про рух рідини в тріщинуватій породі
Наявність в породі
Існуванням перетікання між порами й тріщинами, або мікро- і макротріщинами;
Наявність рідких великих тріщин, що порушують радіальний або плоский характер потоку та не дозволяють розглядати фільтраційне середовище як суцільне (в таких випадках можливо порушення лінійного закону фільтрації).
Наявністю в багатьох випадках яскраво вираженої анізотропії (фільтраційних властивостей тріщинуватого середовища в різних напрямках).
Слайд 16Чисто тріщинувата порода, у якої блоки є непроникними і їхня пористість
Тріщинно-пориста порода — проникність породи переважно визначається проникністю тріщин, а пористість — пористістю (кавернозністю) блоків.
Тріщинно-тріщинна, або нерівномірно тріщинувата порода із двома або більше системами тріщин істотно різного розкриття — густа мережу мікротріщин різного генезису та відносно рідка мережа крупних тріщин. Такі структури можуть розглядатися як аналоги тріщинно-пористих порід. При цьому мікротріщини як би відіграють роль пор, а макротріщини — власне тріщин.
Типи “пористого середовища”
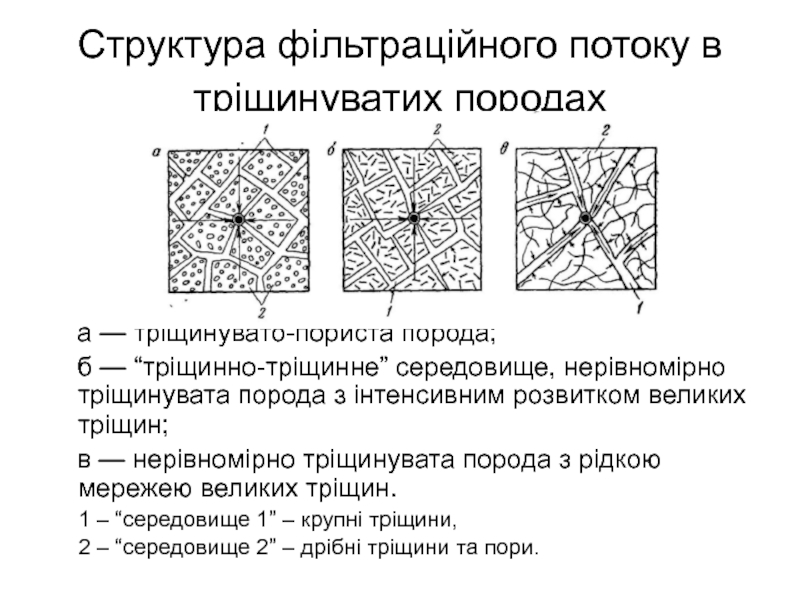
Слайд 17Структура фільтраційного потоку в тріщинуватих породах
а — тріщинувато-пориста
б — “тріщинно-тріщинне” середовище, нерівномірно тріщинувата порода з інтенсивним розвитком великих тріщин;
в — нерівномірно тріщинувата порода з рідкою мережею великих тріщин.
1 – “середовище 1” – крупні тріщини,
2 – “середовище 2” – дрібні тріщини та пори.
Слайд 18“Перерозподіл” напорів
При різкій зміні напору в шарі, оскільки проникність тріщин відносно
За короткий час у системі тріщин відбувається перерозподіл напору. У силу малої проникності блоків фільтрація рідини в них відбувається повільно, і напір може більш-менш довго залишатися на рівні початкового.
У результаті між напором рідини, що заповнює пористий блок, і напором у тріщинах виникає “стрибок”. Зникнення стрибка, а отже, і перерозподіл напорів буде здійснюватися поступово в результаті перетікання частини рідини із блоків у тріщини.
Подібні процеси відбуваються і у «тріщинно-тріщинних» породах
Слайд 19Напрямки вивчення процесів фільтрації в тріщинуватих породах
Тріщинувата порода розглядається як
має безперервні властивості.
Тріщинувата порода розглядається як середовище, розбите системами правильно розташованих тріщин з відомою геометрією процесів фільтрації та параметрами тріщинуватості гірських порід (розкриття тріщин, інтенсивність розтріскування породи, орієнтацію тріщин у просторі) і законами руху рідини в одиночних тріщинах (щілинах).
З точки зору теорії фільтрації перший підхід є значно більш загальним. У той же час у ряді випадків при наявності рідкої мережі великих тріщин їхніми розмірами й конфігурацією не можна зневажити без істотних погрішностей у гідродинамічних розрахунках.
Слайд 20Застосування теорії нестаціонарної фільтрації рідини в тріщинувато-пористій породі
Основні положення нестаціонарної
Тріщинувата порода представляється у вигляді двох пористих середовищ, вкладених одне в інше, з порами різних масштабів.
Тоді рух рідини можна розглядати роздільно в системі крупних тріщин (середовище 1), що розділяють пористі блоки, і в системі блоків (середовище 2).
При цьому між обома середовищами буде відбуватися обмін рідиною.
Слайд 21Схеми гетерогенної структури гірської породи
б) Гетерогенна – блокова.
Слайд 22Математична модель
При прийнятих передумовах фільтрація рідини в такій породі
де Н1,Н2, К1,К2, n1,n2 – відповідно напір, коефіцієнт фільтрації та пористість середовищ 1 та2;
βс1, βс2, β – відповідно стисливість середовищ 1 та 2, рідини;
Δ – оператор Лапласа; α – безрозмірний коефіцієнт.
Слайд 23Математична модель
α − безрозмірний коефіцієнт, що характеризує інтенсивність обміну рідиною між
Величина α пов’язана з коефіцієнтом фільтрації, прямо пропорційна питомій поверхні тріщин σ та обернено пропорційна середньому розміру блока l.
Слайд 25Математична модель
При η → 0 рівняння
Даний розв’язок також показав, що рух рідини у тріщинувато-пористому середовищі порівняно з пористим характеризується наявністю часу запізнювання перехідних процесів ( τ ).
Час запізнювання тим більший, чим більше співвідношення коефіцієнтів фільтрації двох середовищ, та чим менша величина п'єзопровідності, що пов’язано з великим об’ємом рідини в мало проникних блоках.
Слайд 26Висновок по математичній моделі (наближення результатів)
Г.І. Баренблаттом і Ю.I
Тому, якщо час розглянутих процесів (t) достатньо великий в порівнянні з (τ), то для розрахунків можна користуватися звичайними рівняннями фільтрації в пористому середовищі, тобто рівнянням Тейса або Тейса — Джейкоба.
Слайд 28 Підходи до визначення геофільтраційних параметрів
Визначення геофільтраційних параметрів на основі безпосереднього
Визначення геофільтраційних параметрів за методикою для звичайних зернистих середовищ на основі рішення рівняння Тейса - Джейкоба, коли час відкачки значно більше характерного часу запізнювання ( τ ), з використанням асимптотичної частини дослідних закономірностей зміни рівня.
При використанні другого підходу слід встановити:
– наскільки реальна картина фільтрації відповідає математичній моделі середовища з “подвійною пористістю;
– наявність на графіках зміни рівня асимптотичної ділянки, що відповідає рівнянню Тейса-Джейкоба.
Слайд 29Недоліки першого підходу
Складність визначення параметрів диференційних рівнянь, що відповідають умовам досліду.
Аналітична
Громіздкість розв'язку.
Значна розбіжність результатів по окремим свердловинам за даними дослідних кущових відкачувань.
Тому доцільно використовувати метод Джейкоба
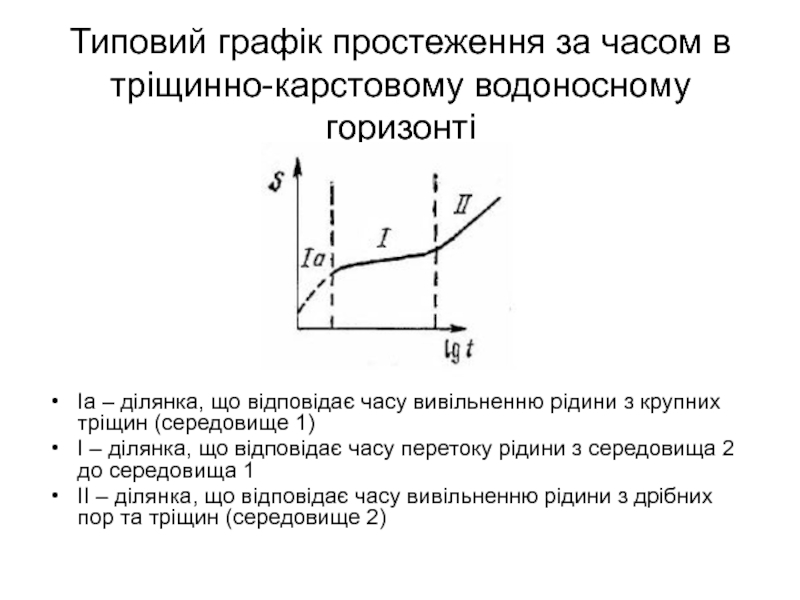
Слайд 30Типовий графік простеження за часом в тріщинно-карстовому водоносному горизонті
Іа – ділянка,
І – ділянка, що відповідає часу перетоку рідини з середовища 2 до середовища 1
ІІ – ділянка, що відповідає часу вивільненню рідини з дрібних пор та тріщин (середовище 2)
Слайд 31Коротка характеристика ділянок
графіка S – lg(t)
Ділянка Іа.
В окремих випадках
за методом Тейса-Джейкоба можна визначити
параметри по ділянках Іа та ІІ.
Ділянка І.
Чим менша різниця в пористості двох середовищ, тим
ця ділянка менше виражена на графіку S – lg(t).
Практична її тривалість від кількох годин до кількох діб
(при цьому вона легко може бути прийнята за ділянку
квазістаціонарного режиму).
Ділянка ІІ.
Квазістаціонарний режим фільтрації
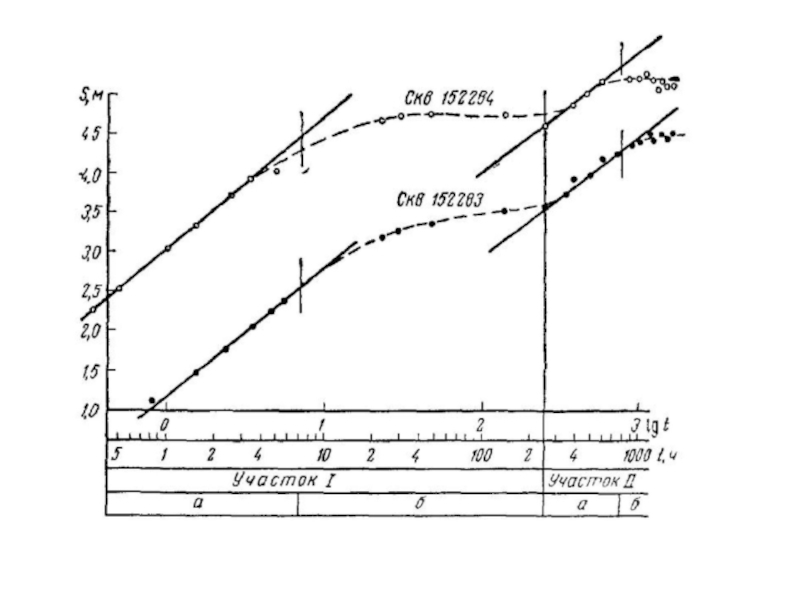
Слайд 32Приклад визначення геофільтраційних параметрів із застосуванням методу Джейкоба
Відкачування виконувалось з напірного
Обробка виконана методом часового простеження.
Всі ділянки на графіку представлені у повному вигляді.
Слайд 35Інтерпретація результатів
Параметри шару, визначенні по ділянках Іa та
П’єзопровідність, визначена по ділянці 1а, виявляється нереально високою й перевищує значення по ділянці IIа в 10-20 разів.
Співставлення величин пружної водовіддачі показує, що середовище 1 (великі тріщини й карстові порожнини) дає лише близько 5—10% від загальної пружної водовіддачі шару.
Збіг водопровідностей також свідчить, що на ділянці II ще не позначається вплив притоку з ріки. Цей чинник виявився пізніше (ділянка II, б), коли рівень води поступово стабілізувався.
Проведений аналіз підтверджує, що досліджуваний водоносний горизонт характеризується «подвійною пористістю».
Розраховані за методом Джейкоба значення коефіцієнтів водопровідності виходять досить надійними. Коефіцієнт п’єзопровідності визначається характером розвитку депресії та потребує перевірки іншими способами простеження.
Слайд 37ОСОБЛИВОСТІ ОБРОБКИ Й ІНТЕРПРЕТАЦІЇ
РЕЗУЛЬТАТІВ ДОСЛІДНИХ РОБІТ В УМОВАХ
ТРІЩИНУВАТИХ І ТРІЩИННО-КАРСТОВИХ
ВОДОНОСНИХ ГОРИЗОНТІВ
(частина
Слайд 38Розглядаються питання:
Особливості інтерпретації результатів дослідних робіт в умовах тріщинно-пористих водоносних горизонтів.
Водоносні
Водоносні горизонти в анізотропних тріщинуватих породах.
Слайд 39Автомодельна функція
Шляхом моделювання на ЕОМ (Г.І.Баренблатт, Ю.П.Желтов, І.Н.Кочина,1960) було встановлено,
Для цього була розрахована спец. «автомодельна функція», що характеризує залежність безрозмірного тиску від параметрів математичної моделі нестаціонарної фільтрації. Отримані результати порівнювались із даними розрахованими для умов пористого середовища.
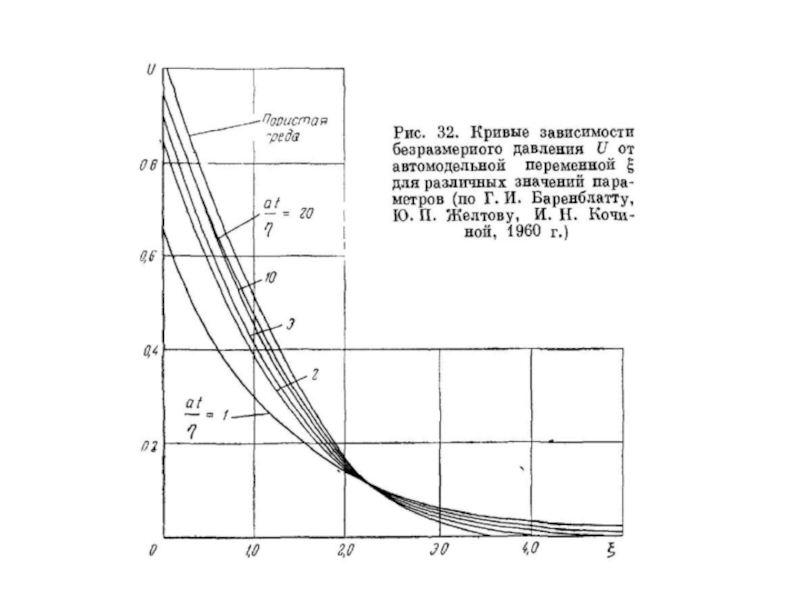
Слайд 40Параметри
“автомодельної функції”
Автомодельна змінна
Криві побудовані для різних
При зростанні (що може бути або при
η → 0, або при t →∞) розподіл тиску в тріщинуватій породі прагне до розподілу його у звичайному пористому середовищі. Як видно з малюнка, крива депресії в тріщинуватому шарі є більше пологою, ніж у звичайному пористому.
Слайд 42Зона “надпровідності”
Аналіз графіку, показує, що в еквівалентному зернистому пласті поблизу дослідної
Радіус такої зони у слабо тріщинуватих пластах змінюється в межах кількох метрів, а в сильно тріщинуватих може досягати 150-200м. Це пов'язано з дренуючим впливом крупних тріщин. Це зона “надпровідності”.
Коефіцієнти п'єзопровідності відповідно у першому випадку будуть занижені, у другому – завищені.
Слайд 43Приклади та “залежності”
Встановлено, що при невеликій тривалості досліду (відкачування) значення коефіцієнтів
Аналогічна картина буде спостерігатися в інтенсивно тріщинуватих й закарстованих породах, коли розкриття тріщин досить великі, тому, що при високій проникності окремих великих тріщин абсолютні зниження міняються мало в міру віддалення спостережних свердловин від дослідної.
Слайд 44Приклади та “залежності”
Незважаючи на те, що з часом розподіли напорів у
У високо проникних пластах при невеликих зниженнях рівня (перші десятки сантиметрів) розходження можуть виявитися істотними, а коефіцієнти водопровідності, розраховані по площинним графікам, будуть значно перевищувати результат розрахунку по часовим і комбінованим (до 5-10 разів).
Слайд 45Приклади та “залежності”
Характерною рисою шарів з інтенсивно розвинутою тріщинуватістю є видиме
Слайд 47Приклади та “залежності”
На графіку добре видно, що зі збільшенням відстані темп
Аналіз результатів дослідних відкачок в інтенсивно тріщинуватих й закарстованих пластах показує, що в якості розрахункових варто приймати значення коефіцієнтів п’єзо- або рівнепровідності, що отримані по спостережних свердловинах, віддалених від дослідної на відстань не менш 1,5—2h (h — потужність горизонту).
Більш обґрунтовані розрахункові значення можуть бути прийняті по графіках а = f(г) на ділянці, де наростання а практично припиняється або стає незначним.
Ця задача вирішується при досить великій кількості різновіддалених спостережних свердловин (не менш 5-6 свердловин).
Слайд 48Складність інтерпретації результатів
При вирішенні питання про виділення на графіку
В умовах, коли графік чітко диференційований, виділення на ньому асимптотичної ділянки II не викликає труднощів.
При впливі зовнішніх меж пласта на діагностування графіків ускладнюється, тому, що:
– потрібна більша тривалість дослідів, щоб вплив мікро неоднорідності шару вже не позначався;
– при великій тривалості дослідів починає позначатися вплив меж, що приводить до деформації та виродження ділянки II для свердловин поблизу границь.
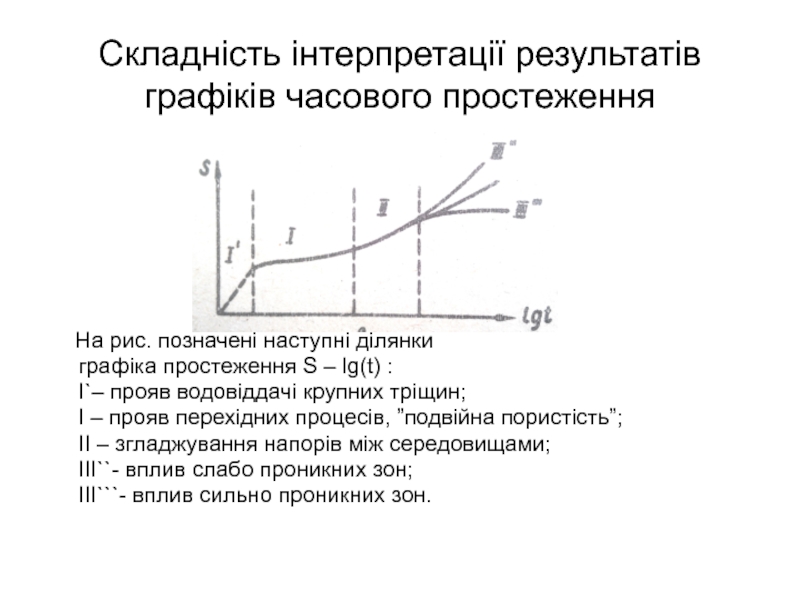
Слайд 49Складність інтерпретації результатів
графіків часового простеження
На рис. позначені
графіка простеження S – lg(t) :
І`– прояв водовіддачі крупних тріщин;
І – прояв перехідних процесів, ”подвійна пористість”;
ІІ – згладжування напорів між середовищами;
ІІІ``- вплив слабо проникних зон;
ІІІ```- вплив сильно проникних зон.
Слайд 50Приклади та “залежності”
Роль комбінованого простеження
Істотну допомогу при аналізі вірогідності отриманих
На них, як правило, пропадає видимість прямолінійності ділянки несправжнього стаціонарного режиму, що добре видно на прикладі відкачки із св. куща 40 на Майкайнарській мульді при порівнянні (співставленні) графіків S — lg(t) і S — lg(t/r2).
Слайд 51Приклади та “залежності”
(Майкайнарська ділянка)
Схема куща 40 (Майкайнарська
Потужність водоносного горизонту 200м. Потужність верхньої, найбільш обводненої зони 100м.
Слайд 52Приклади та “залежності”
(простеження в часі)
Характерний графік часового простеження (S — lg(t))
Слайд 53Приклади та “залежності”
(простеження за площею)
Графіки простеження за площею по кущу 40:
Слайд 55Приклади та “залежності”
(комбіноване простеження)
Графіки
Промінь Ю по кущу свердловин 1-40м, 2-60м, 3-140м, 4-473м.
Промінь С по кущу свердловин 1-60м, 2-120м, 3-43-м, 4-900.
Слайд 57Приклади та “залежності”
(відкачування в умовах рівномірно тріщинуватих пластів)
В умовах звичайних рівномірно
Однак площинні графіки повинні будуватися лише на час, що відповідає виходу графіків S — lg(t/r2) на асимптотичну гілку.
Відповідно, у таких умовах будуть отримані коефіцієнти п’єзо провідності близькі до реальних.
Прикладом подібних умов може служити Розентальска ділянка (Саксонська Швейцарія).
Слайд 58Приклади та “залежності”
(відкачування в умовах рівномірно тріщинуватих пластів)
Об'єктом випробування
Паралельність і лінійність площинних графіків простеження також свідчить про квазістаціонарний режим.
Параметри отримані по площинним і комбінованим графікам практично збігаються, що свідчить про їхній дійсний характер.
Однак у цьому випадку ефект «подвійної пористості» не фіксується практично й на графіках часового простеження, що зв’язано або з відсутністю цього ефекту, або з дуже маленьким часом запізнювання (τ).
Слайд 59Приклади та “залежності”
(відкачування в умовах рівномірно тріщинуватих пластів)
Площинне простеження
Слайд 60Приклади та “залежності”
(в умовах рівномірно тріщинуватих пластів)
Комбіноване простеження на відстанях r
Слайд 62Приклади та “залежності”
(Уральська ділянка)
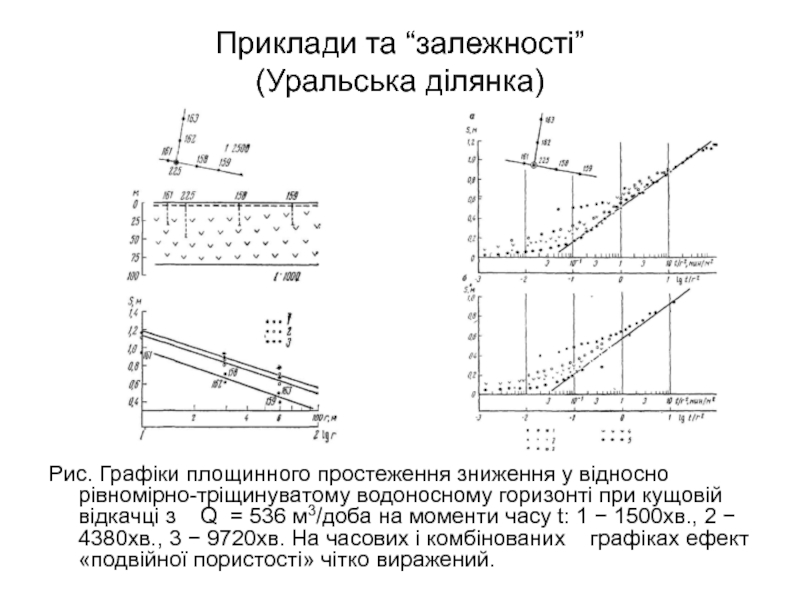
Рис. Графіки площинного простеження зниження у відносно рівномірно-тріщинуватому водоносному горизонті при кущовій відкачці з Q = 536 м3/доба на моменти часу t: 1 − 1500хв., 2 − 4380хв., 3 − 9720хв. На часових і комбінованих графіках ефект «подвійної пористості» чітко виражений.
Слайд 64Приклади та “залежності”
(Уральська ділянка)
Комбіновані графіки виходять на одну
Час запізнювання в даному прикладі не перевивав 1,4 —2,9год.
Слайд 67Висновки:
У тріщинних середовищах, що характеризуються одною системою пустот або двома,
Слайд 68Висновки:
Асимптотичні ділянки комбінованих графіків по різних спостережних
Найбільші складності виникають при інтерпретації результатів відкачок з обмежених пластів, складених інтенсивно тріщинуватими й закарстованими породами.
Слайд 69Висновки:
В умовах сполучення ефекту «подвійної пористості» з різними граничними
а) вплив границь проявляється в часових і комбінованих графіках у формі появи кінцевого більше пологої або більше крутої ділянки; розрахункова асимптотична ділянка формується до початку впливу границь; графік має характерну форму;
б) вплив границь, не деформує характерної форми графіків, але змінює кутовий коефіцієнт асимптотичної ділянки графіка;
в) вплив границь деформує характерну форму графіка, не дозволяючи виділити асимптотичну розрахункову ділянка на часових і комбінованих графіках.
В останньому випадку задача розрахунку гідрогеологічних параметрів методом Джейкоба стає невизначеною,
Слайд 71Загальна характеристика
У багатьох випадках, особливо в межах древніх щитів і масивів
До таких порід відносяться родовища так званих тріщинно-жильних води. У цих умовах розмірами й конфігурацією окремих тріщин зневажити не можна, оскільки фільтраційний потік втрачає радіальний характер
Слайд 72Підхід до розрахунку геофільтраційних параметрів
Підхід до розрахунку фільтрації, заснований на
Слайд 73Форми прояву впливу
великих тріщин
1) зниження рівня у двох різновіддалених від
2) зниження рівня в далекій свердловині більше, ніж у ближній, хоча свердловини розташовані по одному променю;
3) у свердловинах, розташованих на різних променях на одній відстані від дослідної, зниження рівня по абсолютній величині різняться на порядок і більше.
Слайд 74Результати дослідних відкачок із сильно метаморфізованих порід архею
Графіки часового простеження
Слайд 75Результати дослідних відкачок із сильно метаморфізованих архею
Відкачка із свердловини №44 (Q
Відкачка зі свердловини №34 (Q = 5,35л/сек). Але одному променю розташовані три спостережливі свердловини на відстанях 25,50 і 150м від дослідної. Зниження рівня відповідно склали 2,03, 2,01 і 1,96м.
У той же час при обох відкачках досдіні закономірності зниження рівня в часі має однаковий характер.
Слайд 77Інтерпретація результатів
З табл. видно, що при відкачці зі свердловини 34 завищені
Дійсно, розрахунок коефіцієнта водопровідності по формулі Дюпюі дав різко завищений результат (див. табл.). У цьому випадку, однак, порушенням радіальності потоку можна зневажити.
При відкачці зі свердловини №44 фактичні зниження виявилися істотно більше розрахункових, що свідчить про те, що основний приплив до свердловини відбувається лише по декількох великих тріщинах.
Слайд 78Інтерпретація результатів
Випадок, коли порушення радіальності потоку проявляється найбільше характерно, можна ілюструвати
Дослідний кущ складався із двох взаємо перпендикулярних променів по дві свердловини в кожному, розташовані на відстанях 25 і 50 м від дослідної.
Один промінь розташований уздовж великої тріщини або зони дроблення, другий — у слабко тріщинуватих породах. Дебіт свердловини дорівнює 6 л/сек. Зниження рівня відповідно: по свердловинах, що розкрила велику тріщину, 16,61 і 12,35м; по свердловинах, що розкрила слабко проникні породи, 0,61 і 0,30м. Як видно, різниця в зниженнях рівня в свердловинах, що розкрили мало проникні породи й тріщину, істотно відмінна й становить відповідно 0,31 і 4,26м. Це свідчить про те, що основна кількість води надходить до свердловини по розкритій тріщині. Дійсно, якщо розрахувати величину Кm по формулі Дюпюі, то по свердловинах, що розкрили тріщину, вона виявляється 13 м2/доба, а в мало проникних блоках 185 м2/доба, що повністю суперечить результатам, отриманим при прокачуваннях відповідних свердловин. Якщо ж розрахувати водопровідність тріщинної зони по свердловинах, що розкрили тріщину, розглядаючи потік у ній як плоскопаралельний і зневажаючи припливом із слабо проникних зон, то з урахуванням двостороннього припливу до дрени при ширині потоку (тріщини) 10м Кm — 1530 м2/доба (чи 765 м2/доба при ширині потоку 20м).
Відповідно, у даних умовах порушенням радіальності потоку зневажити не можна, тому що відстані між тріщинами і їхніми розмірами досить великі й порівнянні з відстанями між свердловинами.
Слайд 79Інтерпретація результатів
У випадках подібних до відкачка зі св. 34 розрахунок по
К = Ктр.·n,
де К и Ктр. — коефіцієнти фільтрації шару й тріщини; n — пористість.
Якщо одна зі свердловин потрапила в слабо проникний блок, а друга в тріщину, значення водопровідності буде різко занижено. При розкритті обома свердловинами слабо проникних порід водопровідність шару може, виявитися істотно завищеною.
Очевидно, що в розглянутих умовах визначення параметрів на основі площинного простеження зміни рівнів при невеликому числі точок замірів практично неможливо.
Однак у ряді випадків можна скористатися загальним графіком S/Q — lg(r), коли за рахунок великої кількості точок, незважаючи на їхнє розсіювання, вдається провести осреднюючу лінію.
Слайд 80Висновок
Розглянуті в даному розділі умови можна охарактеризувати як крайній граничний випадок
Природно, що р таких умовах час запізнювання може бути дуже великий. Тому в ряді випадків досягнення квазістаціонарного режиму виявляється практично неможливим, а отже, завдання визначення параметрів за даними дослідних робіт по суті, нездійсненно.
Слайд 82Загальні положення
У роботах Е. М. Смехова, Е. С. Ромма й інших
У плані визначення розрахункових гідрогеологічних параметрів з урахуванням анізотропії гірських порід найбільший інтерес представляє однорідна прямолінійна анізотропія, коли напрямок головних осей не міняється при зміні координат і властивості середовища залишаються незмінними від точки до точки.
У випадку неоднорідної криволінійної анізотропії вона повинна бути зведена до однорідної прямолінійної, інакше можливості розрахунку параметрів обмежені так само, як і в умовах різкої нерівномірної тріщинуватості.
Слайд 83Метод ізотропної деформації простору
Основним методом рішення фільтраційних завдань
Рішення диференціального рівняння несталої фільтрації в шарі із прямолінійною однорідною анізотропією отримане Н. К. Гавич для умов радіального потоку при трансформації однієї з осей координат у вигляді [34]:
де Кх і Ку — коефіцієнти фільтрації по головних осях координат х та у; r − радіус-вектор у системі координат х та у,
При цьому приймається, що об'ємна інтенсивність тріщинуватості (або водовіддача) залишається постійною незалежно від обраного напрямку:
де ах ау — коефіцієнти п’єзопровідності по різним осям анізотропії.
Слайд 84Метод ізотропної деформації простору
Аналогічний вираз, але
Як і у звичайному ізотропному шарі, за умови, що експонентна функція може бути замінена логарифмічної, тоді вираз
за умови трансформації осі х може бути записаний у вигляді:
Дані залежності показують, що в анізотропному шарі в умовах квазістаціонарної фільтрації темп зниження рівня не залежить від напрямку й визначається середнім геометричним значенням коефіцієнту фільтрації, який можна розглядати як його ефективну величину:
Слайд 85Метод ізотропної деформації простору
Величина зниження рівня в анізотропному шарі залежить від
З огляду на рівність, вираження для зниження рівня на головних осях анізотропії приймають вид:
Таким чином, у свердловинах із прямолінійною неоднорідною анізотропією основні розрахункові параметри по осях анізотропії можуть бути визначені способом Джейкоба з використанням всіх трьох його модифікацій. Розрахункові формули наведені в табл.
Слайд 86
Для визначення параметрів з використанням всіх модифікацій способу Джейкоба необхідно мати
Критерієм необхідності врахування анізотропії при обробці результатів дослідних відкачок є витягнутість і еліпсоподібна форма воронки депресії з істотним розходженням довжин півосей еліпса. Однак питання про кількісну оцінку погрішностей, що виникають при ігноруванні анізотропії, у загальному випадку не вирішений. Тому можлива погрішність повинна оцінюватися в кожному конкретному випадку, після чого можна встановити необхідність врахування анізотропії.
Слайд 88Загальні висновки
1. Тріщинуваті й закарстовані породи в більшості випадків характеризуються подвійною
2. Вибір розрахункових ділянок часових і комбінованих графіків виконується по суті на основі якісного аналізу дослідних закономірностей зміни рівнів у процесі відкачок, тому, що критерій контрольного часу в даних умовах не може бути застосований.
3. Найкращі результати при діагностуванні розрахункових ділянок графіків дає комбіноване простежування. Комбіновані графіки залежно від структури тріщинуватого або тріщинно-карстового середовища й співвідношення фільтраційних і ємнісних властивостей різних типів порожнеч можуть бути представлені:
а) загальним напівлогарифмічним графіком, що формується по
суті без запізнювання (ефект «подвійної пористості» відсутній або практично не проявляється);
б) графіками, аналогічними графіками Болтона, із загальною асимптотичною ділянкою, що формується із запізнюванням;
в) сімейством графіків з паралельними асимптотичними
ділянками, що формуються із запізнюванням.
Слайд 89Загальні висновки
4. У шарах з різко нерівномірною тріщинуватістю
5. Визначення параметрів анізотропних шарів може бути виконано звичайними методами, але з урахуванням зміни форми потоку. Тому всі графіки варто будувати роздільно для свердловин, розташованих на різних осях анізотропії.
6. У зв'язку із запізнюванням формування асимптотичних ділянок для аналізу ступеня впливу границь критерій наведеної відстані (гпр) може бути використаний лише при невеликих значеннях τ. Факт впливу границь може додатково встановлений по початку появи аномальної ділянки, що буде залежати від положення свердловини відносно межі (границі), що не спостерігається при впливі «подвійної пористості».