Е – единичная матрица
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обратная матрица презентация
Содержание
- 1. Обратная матрица
- 2. Алгоритм нахождения обратной матрицы 1
- 3. 2 Находим определитель матрицы. Если он равен нулю, то обратной матрицы не существует.
- 4. 3 Заменяем каждый элемент матрицы его алгебраическим дополнением.
- 5. 4 Полученную матрицу транспонируем.
- 6. 5 Каждый элемент полученной матрицы делим
- 7. 6 Делаем проверку. Для этого перемножаем полученную и исходную матрицы. Должна получиться единичная матрица.
- 8. Пример. Найти матрицу, обратную к матрице
- 9. Применяем алгоритм нахождения обратной матрицы. Решение: Находим
- 10. Находим алгебраические дополнения каждого элемента матрицы: 3 Составляем из полученных значений матрицу:
- 11. Транспонируем ее: Каждый элемент матрицы делим на
- 12. Проверяем: 6
Алгоритм нахождения
обратной матрицы 1 Определяем, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.
Слайд 2Алгоритм нахождения
обратной матрицы
1
Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы
для
нее не существует.
нее не существует.
Слайд 65
Каждый элемент полученной
матрицы делим на определитель
исходной матрицы. Получаем
матрицу,
обратную к данной.
Слайд 76
Делаем проверку. Для этого
перемножаем полученную и исходную
матрицы. Должна получиться
единичная матрица.
Слайд 9Применяем алгоритм нахождения обратной матрицы.
Решение:
Находим определитель:
Матрица квадратная, следовательно обратная матрица для
нее существует.
1
2
Слайд 10Находим алгебраические дополнения каждого элемента матрицы:
3
Составляем из полученных значений матрицу:
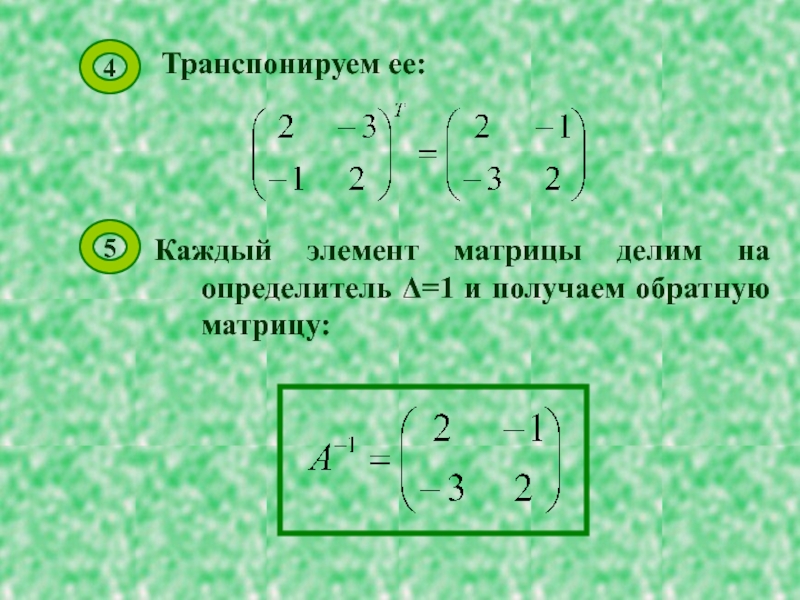
Слайд 11Транспонируем ее:
Каждый элемент матрицы делим на определитель Δ=1 и получаем обратную
матрицу:
4
5
