2007-2008
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия и ее виды презентация
Содержание
- 1. Симметрия и ее виды
- 3. Цели проекта Изучить виды симметрий Рассмотреть виды
- 4. План 1. Понятие «движение» 2.Виды движения
- 5. Движение Движение (в геометрии) - преобразование пространства,
- 6. Виды движений Центральная симметрия Симметрия вращения Осевая симметрия Зеркальная симметрия Поворот Параллельный перенос
- 7. Отображение плоскости на себя Представим себе, что
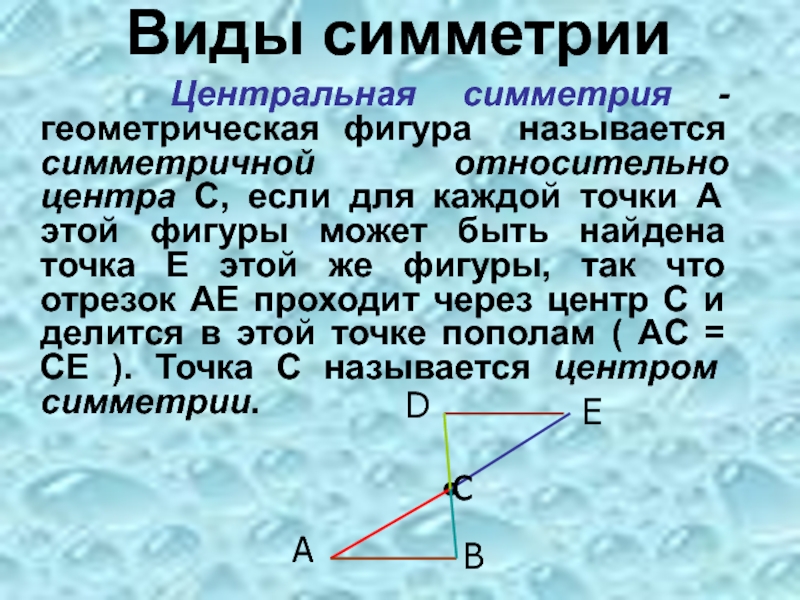
- 8. Виды симметрии Центральная симметрия -геометрическая
- 9. Симметрия вращения Симметрия вращения - тело обладает
- 10. Осевая симметрия Две точки А и А'
- 11. Зеркальная симметрия Геометрическая фигура называется симметричной относительно
- 12. Поворот Поворотом на плоскости около данной точки
- 13. Параллельный перенос Параллельным переносом называется
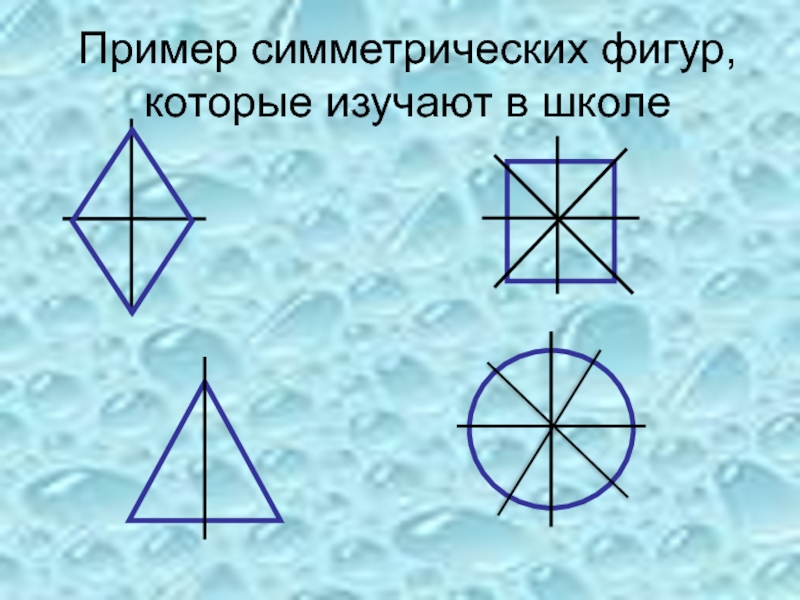
- 14. Пример симметрических фигур, которые изучают в школе
- 15. С симметрией мы встречаемся не только на
- 16. Архитектура Останкинская башня
- 17. Врата в Индии
- 18. Троицкий монастырь
- 19. Дворец с садом
- 20. Храмы на территории Кремля г. Рязани
- 22. Храм в Великом Устюге
- 23. Музей-усадьба академика И.П.Павлова
- 25. Гробница Акбара Эйфелева башня
- 26. Дворец Тадж-Махал
- 27. Симметрия в природе
- 32. Симметрия в быту
- 35. Предметы посуды
- 36. Обои
- 37. Выводы по проделанной работе По проделанной работе
- 38. Литература: ●Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк,И.И.Юдина «Геометрия 7
- 39. Дополнительные материалы www.finam.ru
Слайд 1Самотаева Ирина 9Б
Симметрия и ее виды
ЮВАО
ГОУ СОШ № 1968
Руководитель
Слайд 3Цели проекта
Изучить виды симметрий
Рассмотреть виды симметрий на примерах в природе, быту,
Во время экскурсий и во внеклассной деятельности обратить внимание, где встречается симметрия в нашей жизни
Слайд 4План
1. Понятие «движение»
2.Виды движения
а) Отображение плоскости на себя
б)Центральная симметрия
г)Осевая симметрия
д)Зеркальная симметрия
е)Примеры
ж)Фотографии
3.Выводы
Слайд 5Движение
Движение (в геометрии) - преобразование пространства, сохраняющее свойства фигур (размеры, форму
Движение евклидова пространства - геометрическое преобразование пространства, сохраняющее расстояния между точками. Движение называют собственным или несобственным в зависимости от того, сохраняет ли оно или меняет ориентацию, движение есть ортогональное преобразование.
Слайд 6Виды движений
Центральная симметрия
Симметрия вращения
Осевая симметрия
Зеркальная симметрия
Поворот
Параллельный перенос
Слайд 7Отображение плоскости на себя
Представим себе, что каждой точке плоскости сопоставляется какая-то
м
к
Р
Слайд 8Виды симметрии
Центральная симметрия -геометрическая фигура называется симметричной относительно центра
с
А
Е
В
D
Слайд 9Симметрия вращения
Симметрия вращения - тело обладает симметрией вращения, если при повороте
Слайд 10Осевая симметрия
Две точки А и А' плоскости называются симметричными относительно прямой
Соответствие, при котором каждой точке А сопоставляется симметричная ей относительно прямой с точка А', называется осевой симметрией. Прямая с называется осью симметрии.
Две фигуры F и F' называются симметричными относительно оси с, если каждой точке одной фигуры соответствует симметричная точка другой фигуры.
Фигура F называется симметричной относительно оси с, если она симметрична сама себе.
При симметрии прямые переходят в прямые, причем сохраняются расстояния и углы.
Представление об осевой симметрии дает перегибание листа бумаги. При этом линия сгиба будет осью симметрии, а каждая точка листа совместится с симметричной точкой
В природе оси симметрии имеют листья деревьев, лепестки цветов, бабочки, стрекозы
Слайд 11Зеркальная симметрия
Геометрическая фигура называется симметричной относительно плоскости S , если для
Симметрия плоских фигур.
Зеркально-осевая симметрия. Если плоская фигура ABCDE ( рис.107 ) симметрична относительно плоскости S ( что возможно, если только плоская фигура перпендикулярна плоскости S ), то прямая KL, по которой эти плоскости пересекаются, является осью симметрии второго порядка фигуры ABCDE. В этом случае фигура ABCDE называется зеркально-симметричной.
Слайд 12Поворот
Поворотом на плоскости около данной точки называется такое движение, при котором
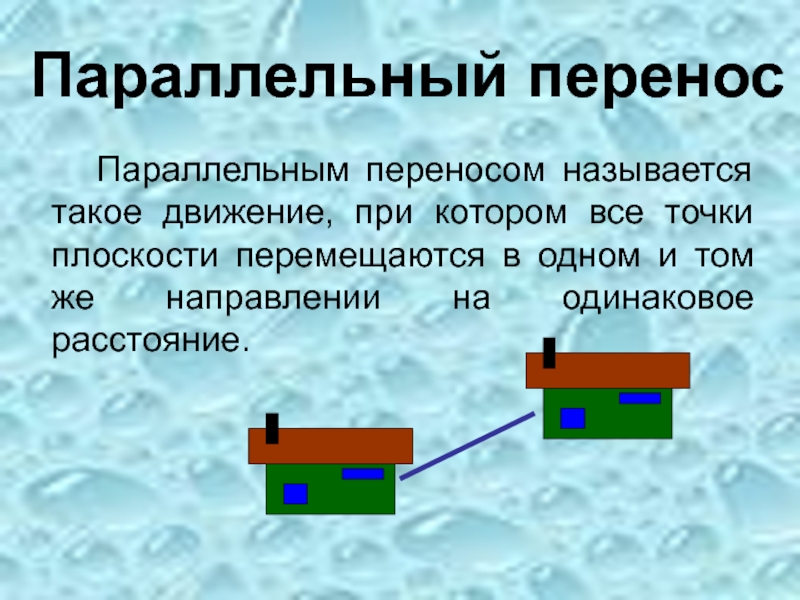
Слайд 13Параллельный перенос
Параллельным переносом называется такое движение, при котором все
Слайд 15С симметрией мы встречаемся не только на уроках, но и в
Слайд 37Выводы по проделанной работе
По проделанной работе мы узнали, что такое симметрия.
Мы узнали, что симметрия используется во всех отраслях нашей жизни – это природа и быт. С давних пор симметрия используется в архитектуре. Даже самые известные памятники архитектуры построены на основе симметрии.
Многие деревья и растения имеют симметричные ветви, листья.
В нашей жизни можно увидеть её в орнаментах обоев и многом другом.
В симметрии заключается красота, пропорции и эстетика всей нашей жизни.
Слайд 38Литература:
●Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк,И.И.Юдина «Геометрия 7 -9»
●Фотографии, сделанные учащейся 9-б класса
●Internet.
●Работы, выполненные учащимися 9-б класса.