t:
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование ВС. Обслуживание с ожиданием. (Тема 3.1.1) презентация
Содержание
- 1. Моделирование ВС. Обслуживание с ожиданием. (Тема 3.1.1)
- 3. СВОЙСТВО ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ) P0(a+t) = e-μ(a+t) P0(a) = e-μa Pa(t)
- 4. СВОЙСТВО ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ) e-μ(a+t) = e-μa⋅Pa(t)
- 5. РАСПРЕДЕЛЕНИЕ ЭРЛАНГА (ГАММА-РАСПРЕДЕЛЕНИЕ С ЦЕЛОЧИСЛЕННЫМ ПАРАМЕТРОМ B)
- 6. МНОГОКАНАЛЬНАЯ СИСТЕМА ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ G/G/M
- 7. ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ ОБСЛУЖИВАНИЕ ПОСЛЕ T0 моменты поступления
- 8. СЛУЧАЙНЫЙ ПРОЦЕСС МАРКОВА Случайный процесс, для
- 9. ОБСЛУЖИВАНИЕ С ПОТЕРЯМИ Потери заявок имеют
- 10. 3.3.2 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ Постановка
- 11. M-МЕРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС Ξ(T): ξ(t)={ ξ1(t), ξ2(t)…
- 12. Если в момент времени t :
- 13. Пусть на i-й аппарат, свободный от обслуживания
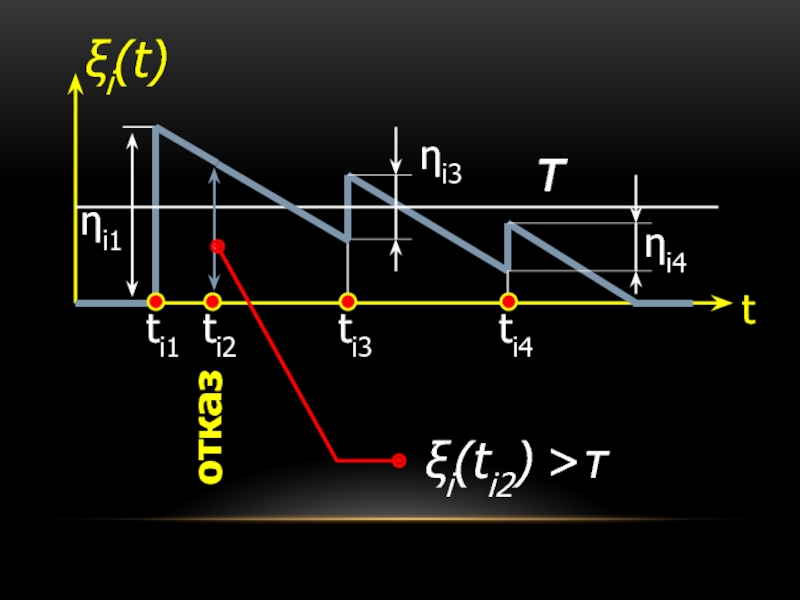
- 14. ξi(ti2) >τ отказ
- 15. 3.3.3 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ Постановка задачи:
- 16. tожидания + tобслуживания < τ заявка обслужена
- 17. ПРИМЕР НЕВОЗМОЖНОСТЬ ЧИСТЫХ ПОТЕРЬ ПРИ ДИСЦИПЛИНЕ ОБСЛУЖИВАНИЯ
- 18. M-МЕРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС Ξ(T): ξ(t)={ ξ1(t), ξ2(t)… ξm(t) } ξi(t) ≤τ Ограничение:
- 19. Пусть на i-й аппарат, свободный от обслуживания
- 20. До момента времени ti1 аппарат свободен от
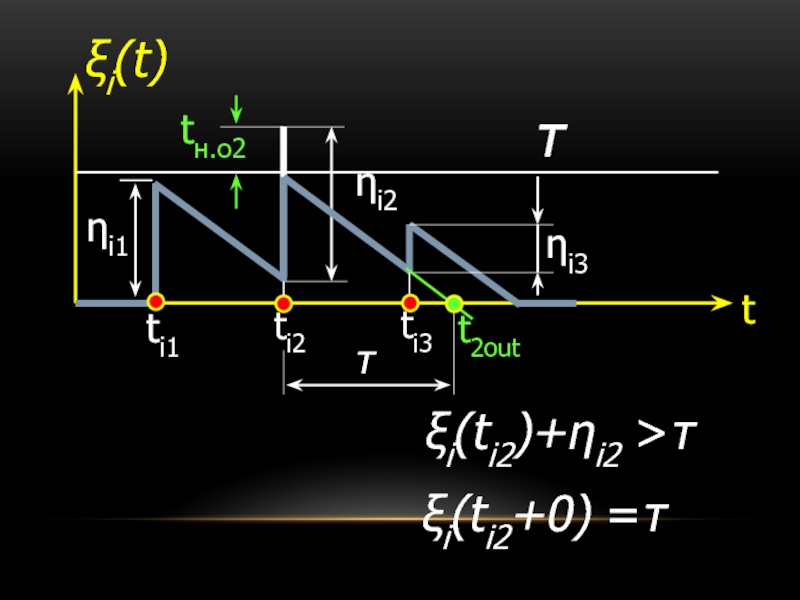
- 21. ξi(ti2)+ηi2 >τ ξi(ti2+0) =τ
- 22. 3.3.4 МОДЕЛИ ПРИОРИТЕТНОГО ОБСЛУЖИВАНИЯ Постановка задачи:
- 23. ПРИОРИТЕТНОЕ ОБСЛУЖИВАНИЕ Заявки: Первого типа (приоритет) Второго
ПРИМЕР ИССЛЕДОВАНИЕ СВОЙСТВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ Пусть Pa(t) – вероятность того, что обслуживание, которое уже продолжается время а, продлиться еще не менее, чем время t.
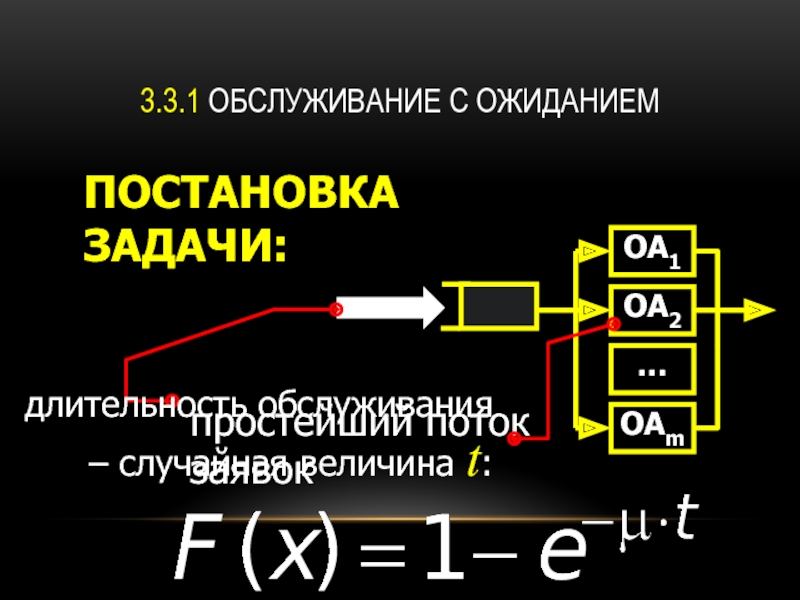
Слайд 13.3.1 ОБСЛУЖИВАНИЕ С ОЖИДАНИЕМ
ПОСТАНОВКА ЗАДАЧИ:
простейший поток заявок
длительность обслуживания – случайная величина
Слайд 2
ПРИМЕР ИССЛЕДОВАНИЕ СВОЙСТВ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Пусть Pa(t) – вероятность того, что обслуживание,
которое уже продолжается время а, продлиться еще не менее, чем время t.
t
0
Слайд 4СВОЙСТВО ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ (ПРОДОЛЖЕНИЕ)
e-μ(a+t) = e-μa⋅Pa(t)
Pa(t) = = e-μt
P0(a+t) =
P0(a)⋅ Pa(t)
не зависит от a
Слайд 5РАСПРЕДЕЛЕНИЕ ЭРЛАНГА
(ГАММА-РАСПРЕДЕЛЕНИЕ С ЦЕЛОЧИСЛЕННЫМ ПАРАМЕТРОМ B)
Плотность распределения:
где
b – целое положительное
число
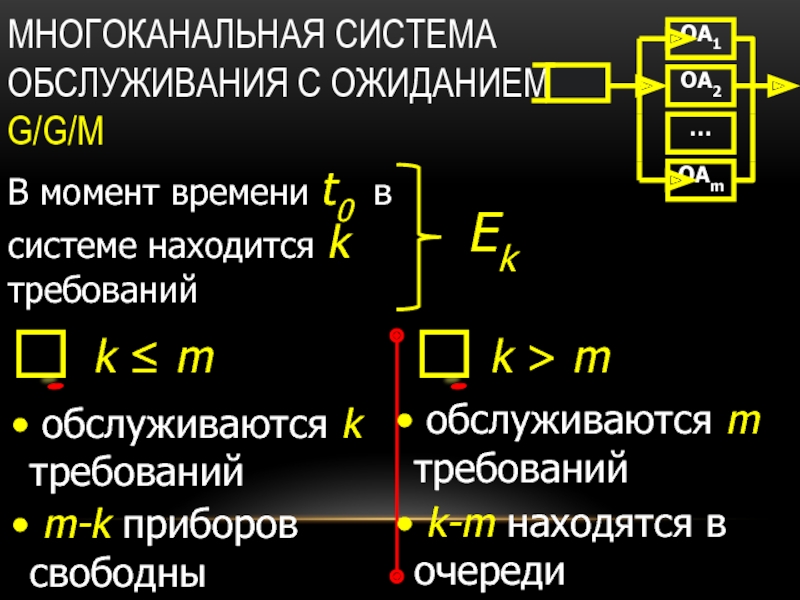
Слайд 6МНОГОКАНАЛЬНАЯ СИСТЕМА ОБСЛУЖИВАНИЯ С ОЖИДАНИЕМ G/G/M
В момент времени t0 в
системе находится k требований
k ≤ m
k > m
обслуживаются k требований
m-k приборов свободны
обслуживаются m требований
k-m находятся в очереди
Ek
Слайд 7ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ ОБСЛУЖИВАНИЕ ПОСЛЕ T0
моменты поступления новых заявок
длительность обслуживания заявок,
поступивших после t0
моменты окончания обслуживаний, производящихся в момент времени t0
не зависят в вероятностном смысле от того, как происходило обслуживание до момента времени t0
Слайд 8СЛУЧАЙНЫЙ
ПРОЦЕСС МАРКОВА
Случайный процесс, для которого будущее развитие зависит только от
достигнутого в данный момент состояния и не зависит от того, как происходило развитие в прошлом
Аналитическое моделирование СМО применимо только к Марковским процессам и системам
!
Слайд 9ОБСЛУЖИВАНИЕ С ПОТЕРЯМИ
Потери заявок имеют место в СМО
с ограниченным временем
ожидания;
с ограниченным временем пребывания;
приоритетного обслуживания;
с ограниченной очередью.
Слайд 10
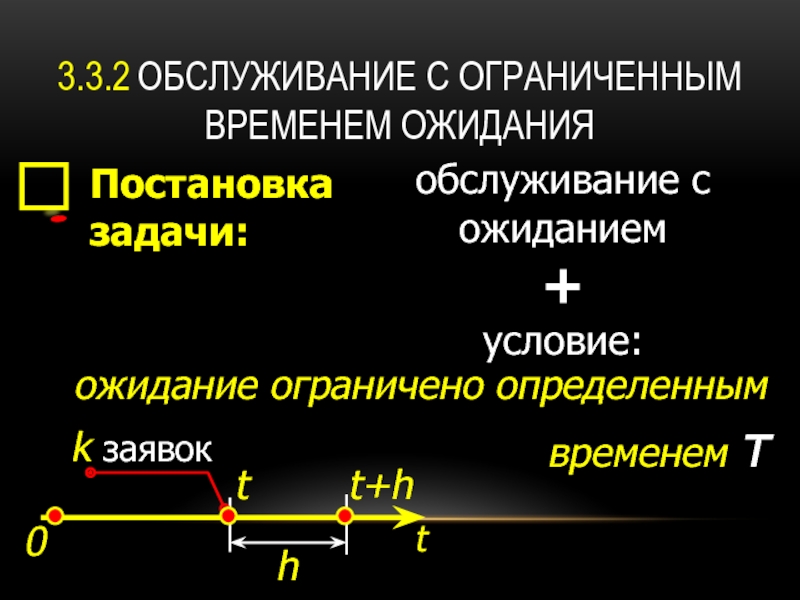
3.3.2 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
Постановка задачи:
обслуживание с ожиданием
+
условие:
ожидание ограничено определенным
временем τ
k заявок
Слайд 11M-МЕРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС Ξ(T):
ξ(t)={ ξ1(t), ξ2(t)… ξm(t) }
где
ξi(t) –
время, которое должно протечь от момента t до освобождения прибора с номером i от обслуживания заявок, поступивших ранее t
Слайд 12Если в момент времени t :
аппарат с номером i
свободен
в системе нет заявок, ожидающих обслуживания
и
ξi(t)=0
Заявка, поступившая в момент t, выбирает прибор с номером i если:
Слайд 13Пусть на i-й аппарат, свободный от обслуживания в момент времени t=0
заявки поступают в моменты времени ti1 , ti2…
необходимые для их обслуживания длительности времени равны соответственно ηi1 , ηi2…
Слайд 153.3.3 ОБСЛУЖИВАНИЕ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
Постановка задачи:
обслуживание с ожиданием
+
условие:
пребывание заявки в
системе ограничено определенным временем τ
Слайд 16tожидания + tобслуживания < τ
заявка обслужена полностью
tожидания < τ
tожидания + tобслуживания
> τ
заявка потеряна с незавершенным обслуживанием
tожидания > τ
чистая потеря (без затраты времени на обслуживание)
Слайд 17ПРИМЕР НЕВОЗМОЖНОСТЬ ЧИСТЫХ ПОТЕРЬ ПРИ ДИСЦИПЛИНЕ ОБСЛУЖИВАНИЯ FIFO
Ординарный поток
раздельное поступление заявок
в СМО
первая заявка покидает СМО
первая заявка покидает СМО
начинается обслуживание второй заявки
вторая заявка покидает СМО
Слайд 19Пусть на i-й аппарат, свободный от обслуживания в момент времени t=0
заявки поступают в моменты времени ti1 , ti2…
необходимые для их обслуживания длительности времени равны соответственно ηi1 , ηi2…
Слайд 20До момента времени ti1 аппарат свободен от обслуживания:
ξi(t) = 0
В момент
времени ti1 при поступлении заявки ξi(t) совершает скачек, причем:
ξi(ti1+0)=ξi(ti1)+ηi1
если ξi(ti1) +ηi1 ≤ τ, то
ξi(ti1+0)=τ
если ξi(ti1) + ηi1 > τ, то
Слайд 223.3.4 МОДЕЛИ ПРИОРИТЕТНОГО ОБСЛУЖИВАНИЯ
Постановка задачи:
Абсолютный приоритет с продолжением незавершенного
обслуживания
Абсолютный приоритет с возобнавлением незавершенного обслуживания
Абсолютный приоритет с потерей незавершенного обслуживания
Слайд 23ПРИОРИТЕТНОЕ ОБСЛУЖИВАНИЕ
Заявки:
Первого типа (приоритет)
Второго типа
обслуживаются независимо от требований второго типа
аналитическая модель обслуживания с ожиданием
обслуживание заявок первого типа эквивалентно отказу ОА
математический аппарат моделирования СМО с ненадежным прибором
