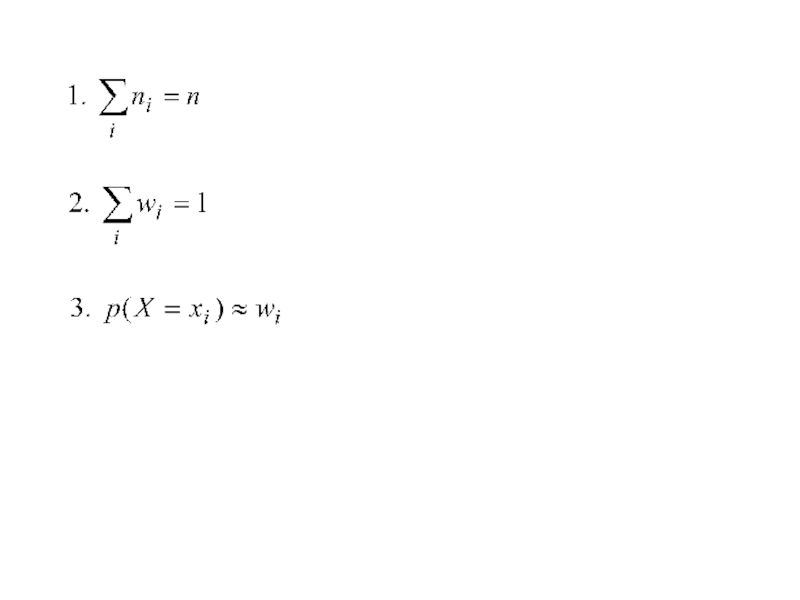Метод моментов
Интервальные оценки
Алгоритм нахождения доверительных интервалов
Оценка а при известной дисперсии
Оценка а при неизвестной дисперсии
Оценка среднего квадратического отклонения
Оценка вероятности события
Проверка статистических гипотез
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА презентация
Содержание
- 1. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- 2. Генеральной совокупностью называют совокупность всех объектов, над
- 3. Способы отбора 1. Отбор, не требующий расчленения
- 4. Наблюдаемые значения xi называют вариантами. Последовательность вариант,
- 6. Полигоном частот называют ломаную, отрезки которой последовательно
- 7. Функция распределения случайной величины Х: F(x) = p(X
- 8. Выборочная характеристика (*) используемая для нахождения приближённого
- 9. Выборочная средняя: 2. Если ui = hxi
- 10. Выборочная дисперсия: 2. Если ui = hxi
- 11. Исправленная выборочная дисперсия: Выборочное среднее квадратическое отклонение: Исправленное выборочное среднее квадратическое отклонение:
- 12. 1-ая группа: N1 элементов 2-ая группа: N2
- 13. Метод максимального (наибольшего) правдоподобия x1, x2, … , xn – выборка
- 14. I. Дискретное распределение p(x1), … ,
- 15. Алгоритм исследования на максимум функции правдоподобия 1. 3. 2. 4.
- 16. Метод моментов I. Оценка одного параметра
- 17. – точечная оценка Интервальной называют оценку, которая
- 19. 1. Пусть Х – непрерывная случайная величина,
- 20. Алгоритм нахождения доверительных интервалов
- 21. Пусть генеральная совокупность имеет нормальное распределение
- 22. или Шаг 2.
- 24. Пусть генеральная совокупность имеет нормальное распределение
- 25. Шаг 2.
- 27. Пусть генеральная совокупность имеет нормальное распределение
- 28. Шаг 2.
- 30. Шаг 2.
- 31. Пусть производятся независимые испытания с неиз-вестной вероятностью
- 32. – случайная величина, имеющая нормальное
- 33. Шаг 2.
- 34. При больших значениях n (порядка сотен)
- 35. Статистической гипотезой называется любое предположение о виде
Генеральной совокупностью называют совокупность всех объектов, над которыми производят наблюдение. Выборочной совокупностью (выборкой) называют часть отобранных из генеральной совокупности объектов. Объёмом совокупности называют количество объектов в ней.
Слайд 1МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Визуализация данных
Точечные оценки
Групповые характеристики
Метод наибольшего правдоподобия
Слайд 2Генеральной совокупностью называют совокупность всех объектов, над которыми производят наблюдение.
Выборочной совокупностью
(выборкой) называют часть отобранных из генеральной совокупности объектов.
Объёмом совокупности называют количество объектов в ней.
Слайд 3Способы отбора
1. Отбор, не требующий расчленения генеральной совокупности на части:
а) простой
случайный бесповторный отбор,
б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается на части:
а) типический,
б) механический,
в) серийный.
Комбинированный отбор.
Слайд 4Наблюдаемые значения xi называют вариантами.
Последовательность вариант, записанных в возра-стающем порядке называют
вариационным рядом.
Частотой варианты называют число ni, показываю-щее сколько раз встречается данная варианта.
Относительной частотой варианты называют отношение частоты к объёму выборки: wi=ni /n.
Статистическим распределением выборки называ-ется перечень вариант и соответствующих им частот или относительных частот.
Слайд 6Полигоном частот называют ломаную, отрезки которой последовательно соединяют точки (xi, ni).
Полигоном
относительных частот называют ломаную, отрезки которой последовательно соединяют точки (xi, wi).
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы, а высоты равны отношению частоты попадания в данный интервал к длине интервала.
Аналогично вводится понятие гистограммы относительных частот.
Визуализация данных
Слайд 7Функция распределения случайной величины Х:
F(x) = p(X
распределения генеральной совокупности.
Эмпирической (выборочной) функцией распределения называют функцию
Обозначим через nx – частоту появления вариант, меньших x. Тогда nx /n – относительная частота появления вариант , меньших x.
F*(x) = nx /n.
Слайд 8Выборочная характеристика
(*)
используемая для нахождения приближённого значения неизвестной генеральной характеристики
, называет-ся её точечной статистической оценкой.
,
Слайд 9Выборочная средняя:
2. Если ui = hxi для всех i, где h
– некоторое число, то
1. Если ui = xi – c для всех i, где с – некоторое число, то
Слайд 10Выборочная дисперсия:
2. Если ui = hxi для всех i, где h
– некоторое число, то
1. Если ui = xi – c для всех i, где с – некоторое число, то
Dв(u) = Dв(x)
Dв(u) = h2Dв(x)
Слайд 11Исправленная выборочная дисперсия:
Выборочное среднее квадратическое отклонение:
Исправленное выборочное среднее квадратическое отклонение:
Слайд 121-ая группа: N1 элементов
2-ая группа: N2 элементов
j-тая группа: Nj элементов
…
…
– групповые средние
– групповые дисперсии
D1, D2, …
Dв=Dвнгр+Dмежгр
– внутригрупповая дисперсия
– межгрупповая дисперсия
Слайд 14I. Дискретное распределение
p(x1), … , p(xn) – вероятности значений x1, …
, xn
Пример. Распределение Пуассона
II. Непрерывное распределение
f(x) – плотность распределения
Слайд 16Метод моментов
I. Оценка одного параметра
Пример. Показательное распределение
II. Оценка двух параметров
Пример. Нормальное
распределение
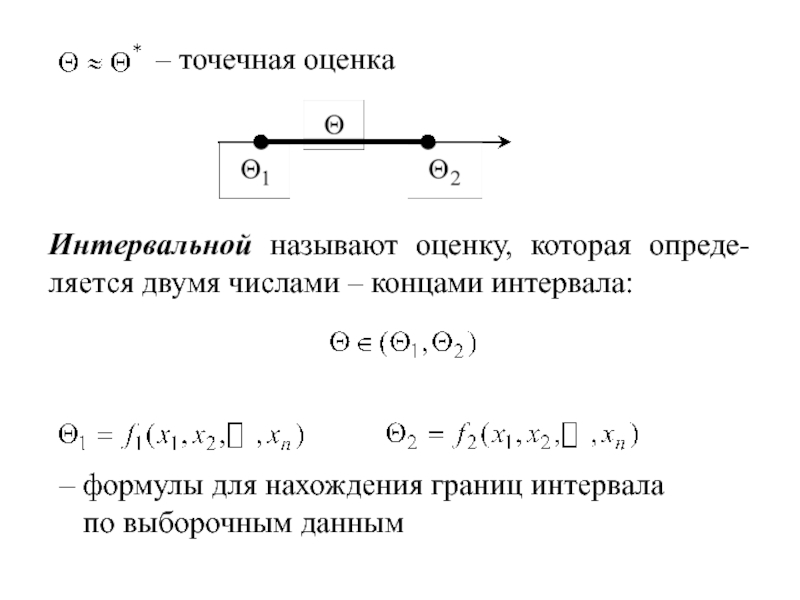
Слайд 17– точечная оценка
Интервальной называют оценку, которая опреде-ляется двумя числами – концами
интервала:
– формулы для нахождения границ интервала
по выборочным данным
Слайд 191. Пусть Х – непрерывная случайная величина,
F(x) – функция
распределения,
f(x) – плотность распределения
f(x) – плотность распределения
(*)
2. Пусть плотность распределения f(x) – чётная функция
(**)
(***)
Слайд 20Алгоритм нахождения доверительных интервалов
или
Вопрос: какой вид имеют функции F(x) и f(x)
?
Слайд 31Пусть производятся независимые испытания с неиз-вестной вероятностью р появления события А
в каждом испытании.
р – ?
2. Находим точечную оценку:
m – число появлений события А при n испытаниях.
Слайд 32
– случайная величина, имеющая нормальное
распределение с нулевым математическим
ожиданием и единичной дисперсией
или
Слайд 35Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона
распределения.
Проверяемую гипотезу называют нулевой (основной), обозначают её Н0.
Конкурирующей (альтернативной) называют гипо-тезу, которая противоречит нулевой, обозначают её Н1.
Задача: проверить, верна ли нулевая гипотеза Н0 при
альтернативной гипотезе Н1?
