- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерное моделирование позы больного ДЦП послехирургической коррекции презентация
Содержание
- 1. Компьютерное моделирование позы больного ДЦП послехирургической коррекции
- 2. Заболевание ЦНС Причина симптомо- комплекса
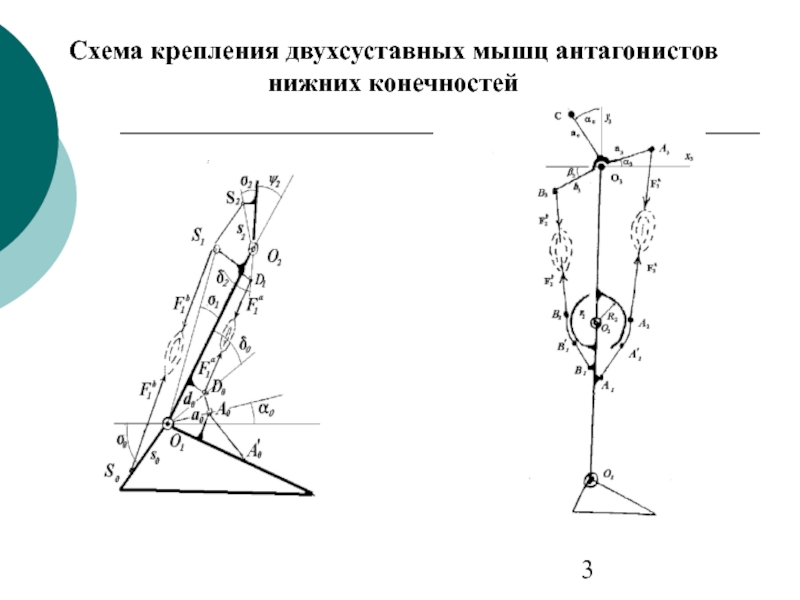
- 3. Схема крепления двухсуставных мышц антагонистов нижних конечностей
- 4. Модель А.Г.Фельдмана мышечных усилий А.Г.Фельдман. Центральные и
- 5. Кинематические соотношения прямая группа hamstring разгибатели пальцев икроножная
- 6. Уравнения равновесия : € Возможная
- 7. Моменты в суставах - моменты, создаваемые односуставными мышцами.
- 8. Управление поддержанием вертикальной позы избыточно с
- 9. Уравнения для определения углов в суставах, описывающих
- 10. Результаты моделирования позы больного при hamstring-синдроме Характерная
- 11. Результаты моделирования позы при hamstring-синдроме
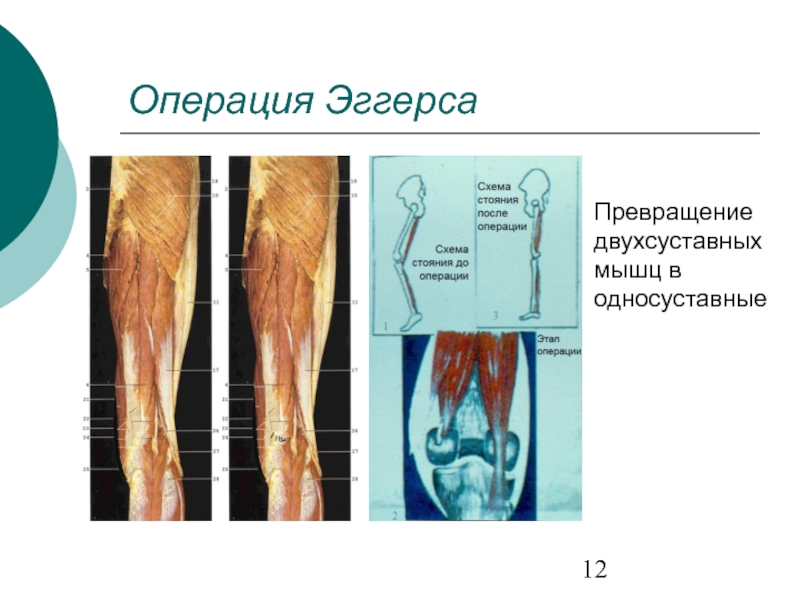
- 12. Операция Эггерса Превращение двухсуставных мышц в односуставные
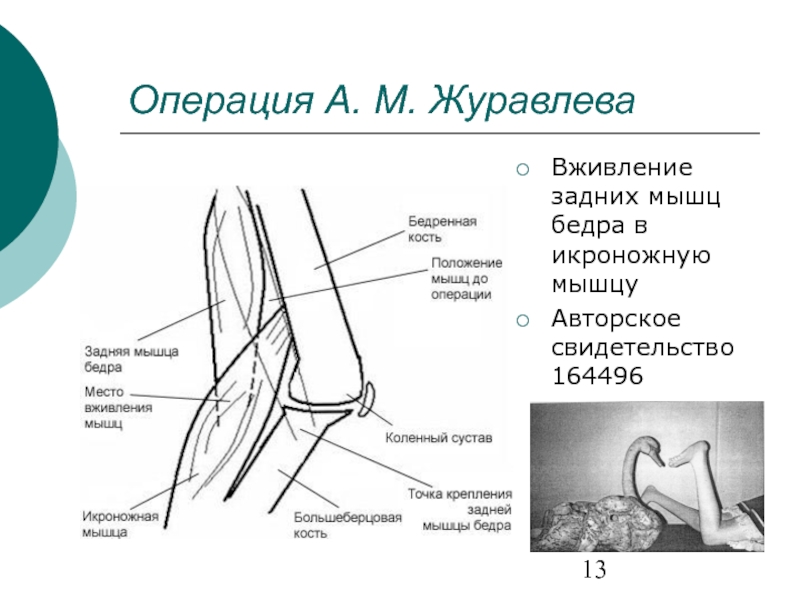
- 13. Операция А. М. Журавлева Вживление задних мышц бедра в икроножную мышцу Авторское свидетельство 164496
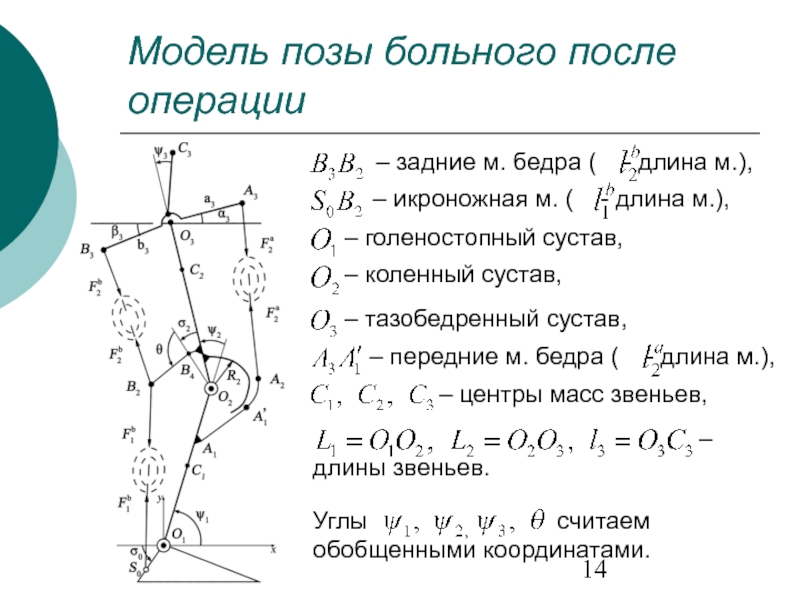
- 14. Модель позы больного после операции – задние
- 15. Обобщенные силы Возможная мощность активных
- 16. Возможные скорости удлинения мышц
- 17. Уравнения равновесия Уравнения равновесия получаем из соотношений: Обобщенные силы Моменты в суставах
- 18. Модель А. Г. Фельдмана мышечных усилий l
- 19. Дополнительные предположения Уравнения равновесия – система
- 20. Уменьшение числа неизвестных Из предположений о позе
- 21. Повышенный тонус прямой мышцы бедра и слабость
- 22. Результаты моделирования позы при hamstring-синдроме после операции
- 23. Поза больного при hamstring-синдроме после операции Поза
Слайд 1Компьютерное моделирование позы больного ДЦП после
хирургической коррекции
П.А.Кручинин, Журавлев А.М,.Хакимов А.И
Кручинин П.А., Никитина О.В. Компьютерное моделирование позы больного ДЦП после хирургической коррекции средствами пакета MATLAB // Труды III Всероссийской научной конференции ПРОЕКТИРОВАНИЕ НАУЧНЫХ И ИНЖЕНЕРНЫХ ПРИЛОЖЕНИЙ В СРЕДЕ MATLAB. СПб, 2007, с. 1558-1567.
Кручинин П.А., Никитина О.В. Моделирование позы больного ДЦП при hamstring-синдроме после хирургической коррекции по А.М.Журавлеву // Вестник МГУ. Математика. Механика. 2010, N 2 , c. 18-23
Слайд 2Заболевание ЦНС
Причина
симптомо-
комплекса
hamstring-
синдрома – черезмерное напряжение
задних
двухсуставных
мышц бедра.
Слайд 4Модель А.Г.Фельдмана мышечных усилий
А.Г.Фельдман. Центральные и рефлекторные
механизмы управления движениями. М.:Наука.
1979
Семейство характеристик тонического
стреч-рефлекса m.gastrocnemius
децеребрированной кошки.
Слайд 6Уравнения равновесия : €
Возможная мощность активных сил
Вертикальная проекция возможной скорости
Обобщенные силы
Qi=0 (i= ψ1, ψ2, ψ3)
Слайд 8 Управление поддержанием вертикальной позы избыточно с точки зрения задачи удержания
Траектории движения центра масс в
проекции на саггитальную плоскость
Размер стопы
Слайд 9Уравнения для определения углов в суставах,
описывающих позу на примере rectus-синдрома.
Уравнения
Сервосвязи ( Результат управления)
Центр масс над голеностопом
вертикальный корпус
Неизвестные
Задано
-”управления” задних групп
двухсуставных мышц
момнеты сил
односуставных мышц
- углы в суставах
минимум “энергозатрат”
-”управления” передней группы двухсуставных мышц бедра
При hamstring-синдроме
Задано
управление для
группы hamstring
- неизвестные
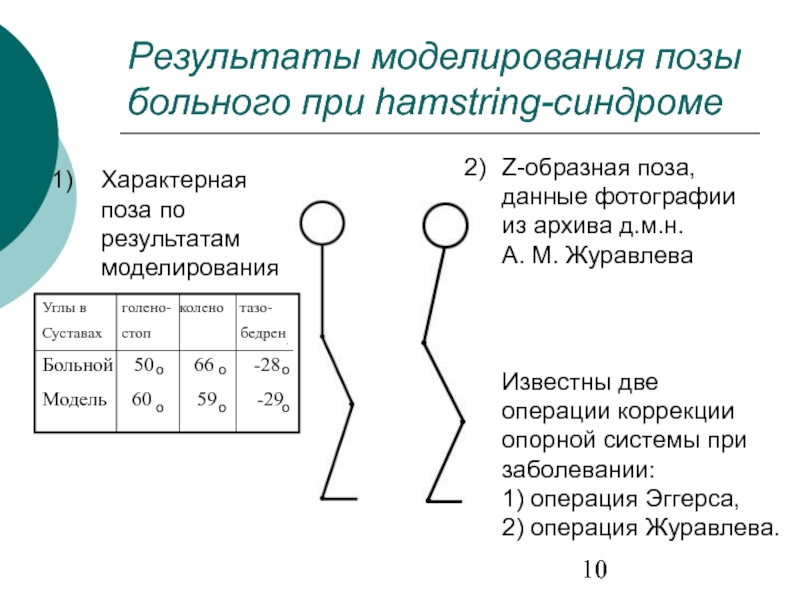
Слайд 10Результаты моделирования позы больного при hamstring-синдроме
Характерная поза по результатам моделирования
Z-образная поза,
из архива д.м.н.
А. М. Журавлева
2)
Известны две
операции коррекции
опорной системы при
заболевании:
1) операция Эггерса,
2) операция Журавлева.
Углы в голено- колено тазо-
Суставах стоп бедрен.
Больной 50 66 -28
Модель 60 59 -29
o
o
o
o
o
o
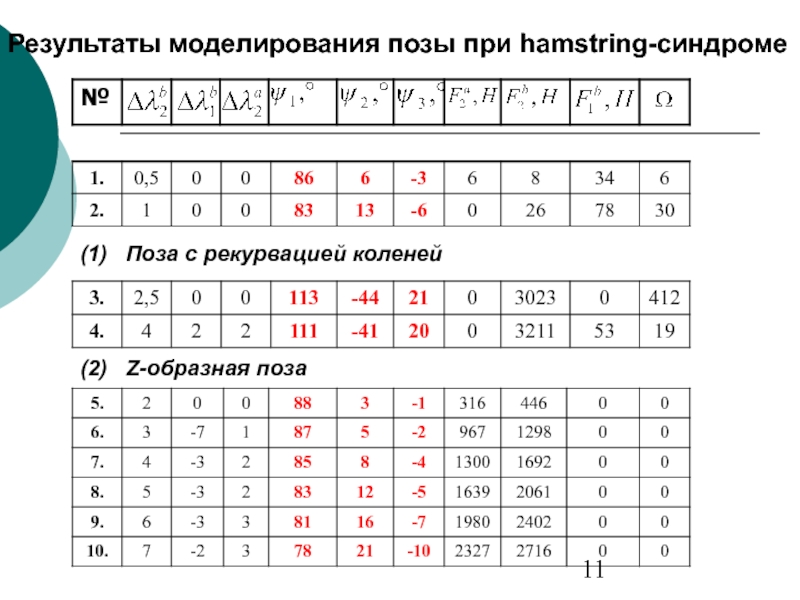
Слайд 11Результаты моделирования позы при hamstring-синдроме
(1) Поза с рекурвацией коленей
(2)
Слайд 13Операция А. М. Журавлева
Вживление задних мышц бедра в икроножную мышцу
Авторское свидетельство
Слайд 14Модель позы больного после операции
– задние м. бедра ( -
– икроножная м. ( - длина м.),
– голеностопный сустав,
– коленный сустав,
– тазобедренный сустав,
– передние м. бедра ( - длина м.),
– центры масс звеньев,
считаем обобщенными координатами.
Углы
– длины звеньев.
Слайд 15Обобщенные силы
Возможная мощность активных сил
Вертикальная проекция возможной скорости центра масс
Обобщенные
Слайд 17Уравнения равновесия
Уравнения равновесия получаем из соотношений:
Обобщенные силы
Моменты в суставах
Слайд 18Модель А. Г. Фельдмана мышечных усилий
l
А. Г. Фельдман. Центральные и рефлекторные
механизмы управления движениями.
М.:Наука. 1979.
примем -модель Фельдмана.
Для сил
Слайд 19Дополнительные предположения
Уравнения равновесия – система 4-х уравнений с 10-ю
неизвестными
Дополним систему:
1)
5) организм обеспечивает минимум некоторого функционала:
2) вертикальный корпус:
3) анатомические особенности:
4) для патологического состояния задано управление :
(из опыта хирургов ).
Слайд 20Уменьшение числа неизвестных
Из предположений
о позе больного
Из уравнений равновесия
переменных с анатомическими ограничениями
проводим
получаем решение:
Минимизацию функционала от 4-х
Слайд 21Повышенный тонус прямой мышцы бедра и слабость икроножной мышцы
Повышенный тонус передней
мышц бедра:
Слабость икроножной мышцы:
Будем решать задачу для фиксированных значений
Уравнение
разрешаем относительно с помощью функции fsolve,
получим зависимость
Задача сведена к нахождению минимума функции
на отрезке