- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Искусственные нейронные сети презентация
Содержание
- 1. Искусственные нейронные сети
- 2. Искусственные нейронные сети Активационные функции 1 2
- 3. Искусственные нейронные сети Активационные функции 3 4
- 4. Искусственные нейронные сети Многослойный персептрон МП -
- 5. Искусственные нейронные сети Многослойный персептрон Количество входных
- 6. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 7. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 8. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 9. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 10. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 11. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 12. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 13. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 14. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 15. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 16. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 17. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 18. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 19. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 20. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 21. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 22. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 23. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 24. Искусственные нейронные сети Алгоритм обучения многослойной нейронной
- 25. Искусственные нейронные сети Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
- 26. Искусственные нейронные сети Обучение “с учителем” и
- 27. Искусственные нейронные сети Ограничение на количество синаптических
- 28. Искусственные нейронные сети
- 29. Искусственные нейронные сети Переобучение, нормализация и подготовка данных
Слайд 1Искусственные нейронные сети
Математическая модель нейрона
Была предложена в 1943 году Урнером Мак-Каллоком
Слайд 4Искусственные нейронные сети
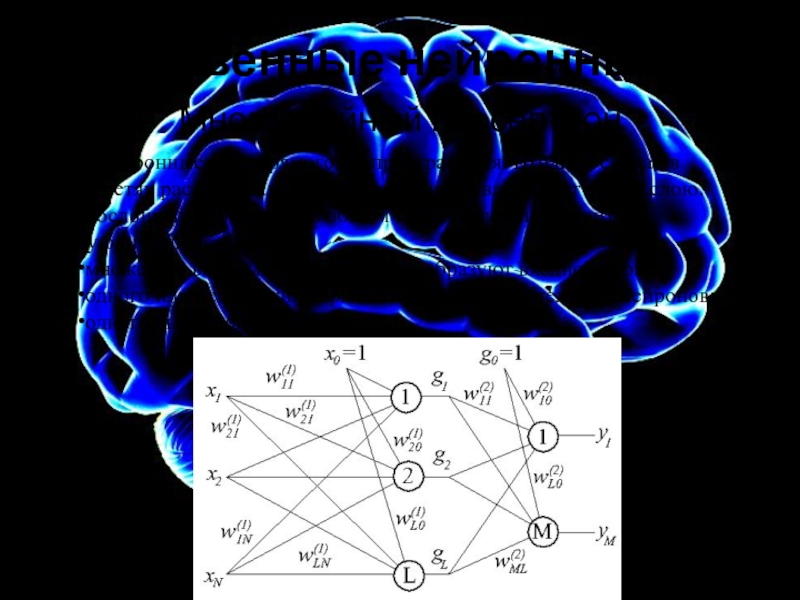
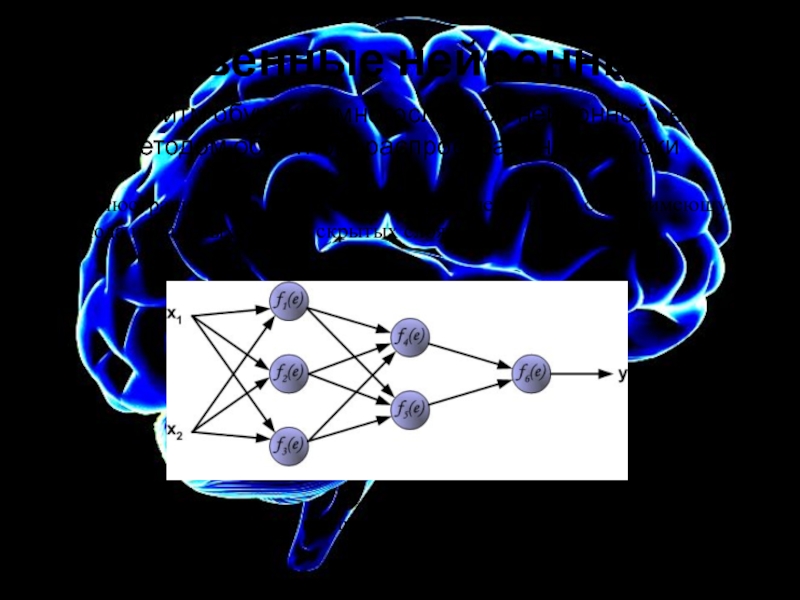
Многослойный персептрон
МП - нейронные сети прямого распространения. Входной сигнал
множества входных узлов, которые образуют входной слой;
одного или нескольких скрытых слоев вычислительных нейронов;
одного выходного слоя нейронов.
Слайд 5Искусственные нейронные сети
Многослойный персептрон
Количество входных и выходных элементов в многослойном персептроне
Свойства:
Каждый нейрон сети имеет гладкую нелинейную функцию активации
Несколько скрытых слоев
Высокая связность
Слайд 6Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
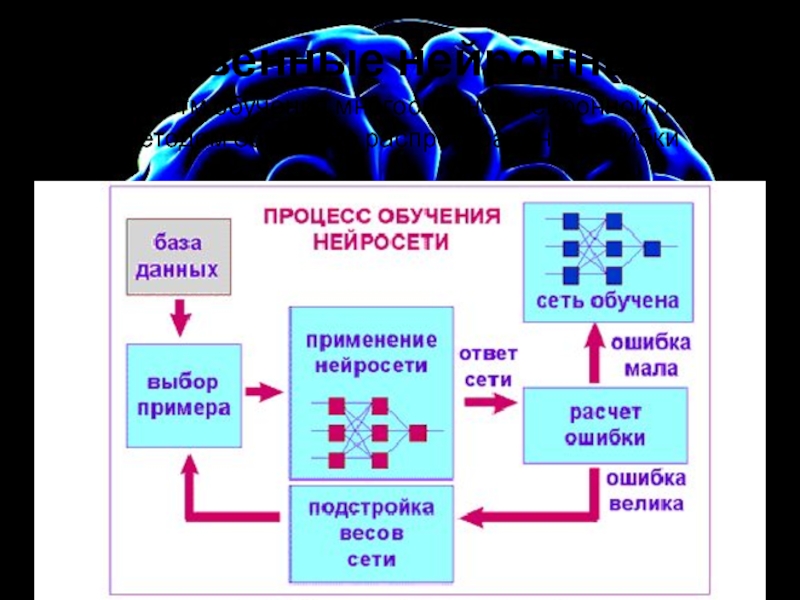
Обучение
При прямом проходе входной вектор подается на входной слой нейронной сети, после чего распространяется по сети от слоя к слою. В результате генерируется набор выходных сигналов, который и является фактической реакцией сети на данный входной образ.
Во время прямого прохода все синаптические веса сети фиксированы. В
о время обратного прохода все синаптические веса настраиваются в соответствии с правилом коррекции ошибок
Слайд 7Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Для
Сигнал е – это взвешенная сумма входных сигналов
Слайд 8Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Чтобы
Обучение – это последовательность итераций (повторений). В каждой итерации весовые коэффициенты нейронов подгоняются с использованием новых данных из тренировочных примеров. Изменение весовых коэффициентов и составляют суть алгоритма, описанного ниже.
Каждый шаг обучения начинается с воздействия входных сигналов из тренировочных примеров. После этого можно определить значения выходных сигналов для всех нейронов в каждом слое сети.
Слайд 9Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Вычисляется
Символы W(xm)n представляют вес связи между сетевым входом xm и нейрона n во входном слое.
Символы yn представляют выходной сигнал нейрона n.
Слайд 10Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
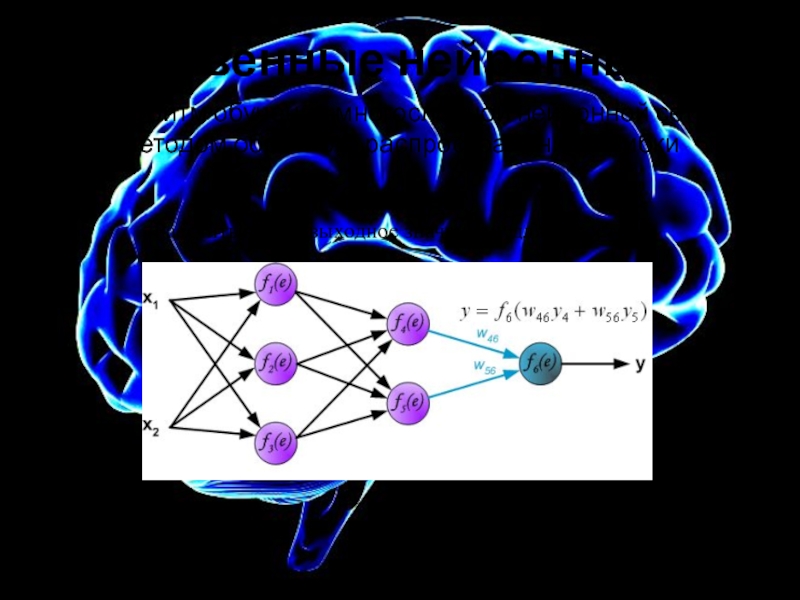
Вычисляется
Слайд 11Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Рассчитывается
Слайд 12Искусственные нейронные сети
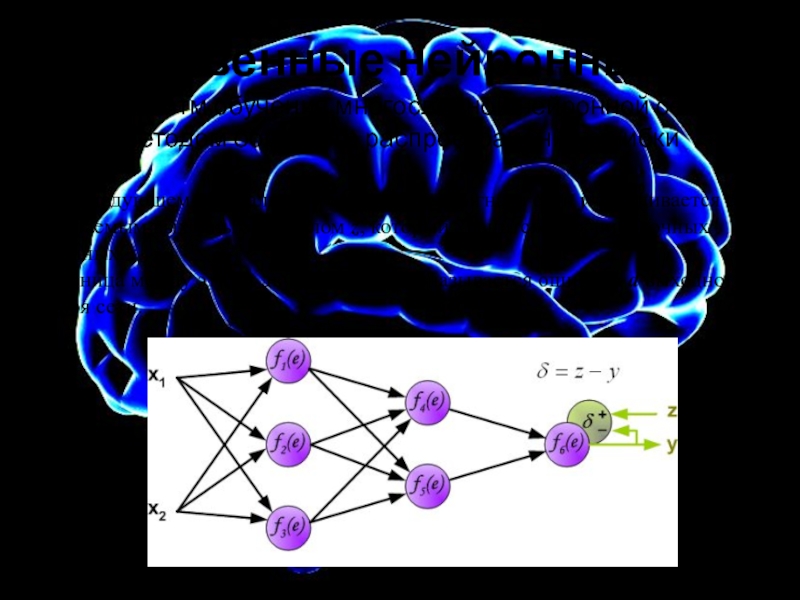
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
На
Разница между этими двумя сигналами называется ошибкой d выходного слоя сети.
Слайд 13Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Невозможно
На протяжении многих лет был неизвестен эффективный метод для обучения многослойной сети.
Только в середине восьмидесятых годов был разработан алгоритм обратного распространения ошибки.
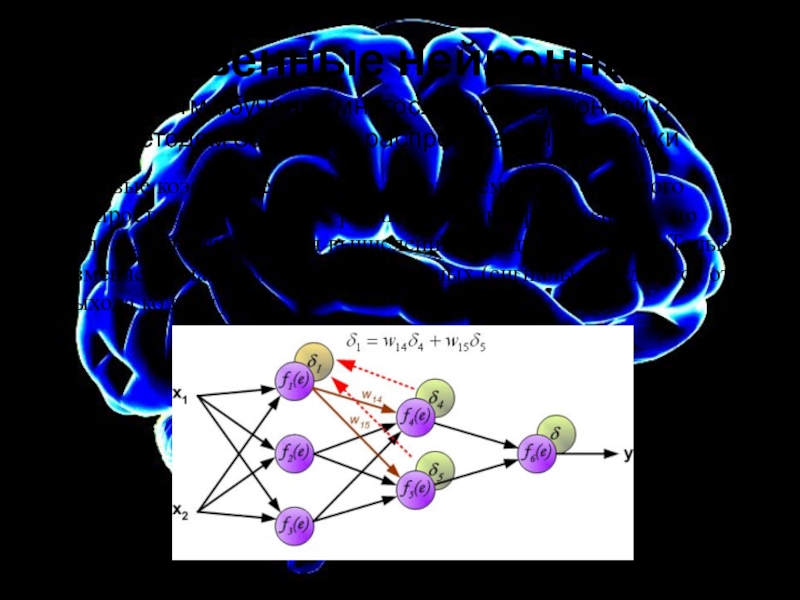
Идея заключается в распространении сигнала ошибки d (вычисленного в шаге обучения) обратно на все нейроны, чьи выходные сигналы были входящими для последнего нейрона.
Слайд 14Искусственные нейронные сети
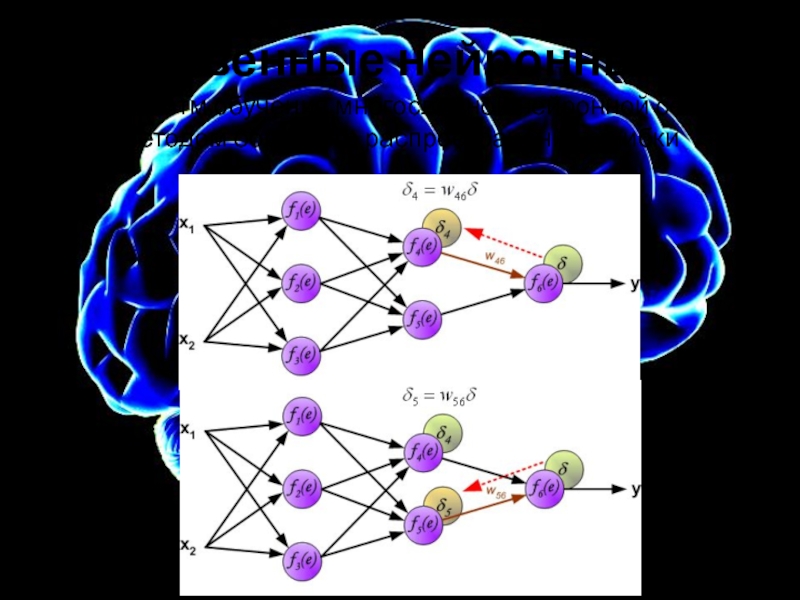
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
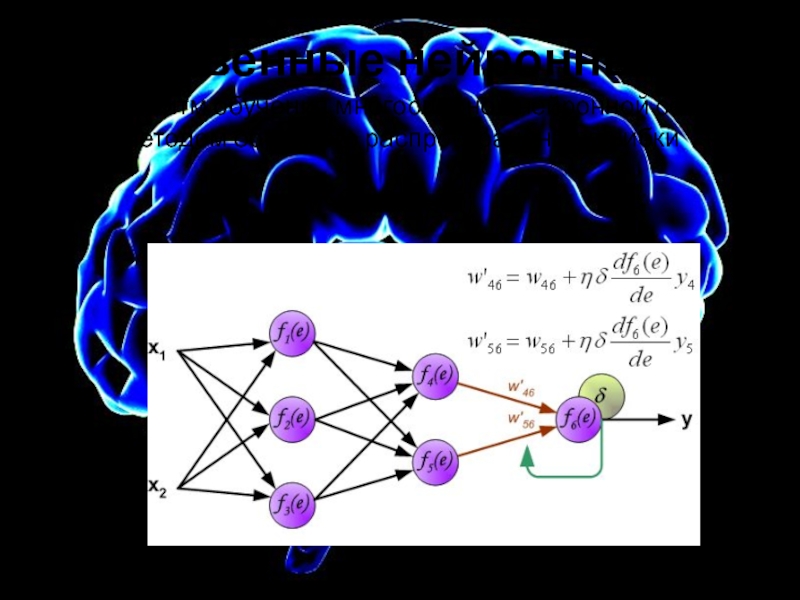
Слайд 15Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Весовые
Слайд 16Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
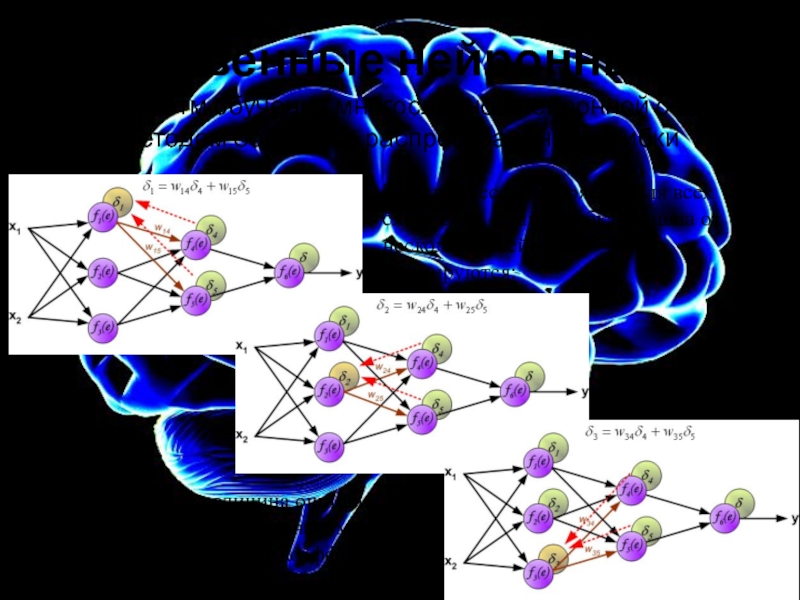
Когда
Этот процесс повторяется для всех слоёв сети. Если ошибка пришла от нескольких нейронов — она суммируются:
Слайд 17Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
При
Для активационной функции типа сигмоида
производная выражается через саму функцию:
что позволяет существенно сократить вычислительную сложность метода обратного распространения ошибки.
1
S(x) = -----------
1 + exp(-x)
S'(x) = S(x)*(1 - S(x))
Слайд 18Искусственные нейронные сети
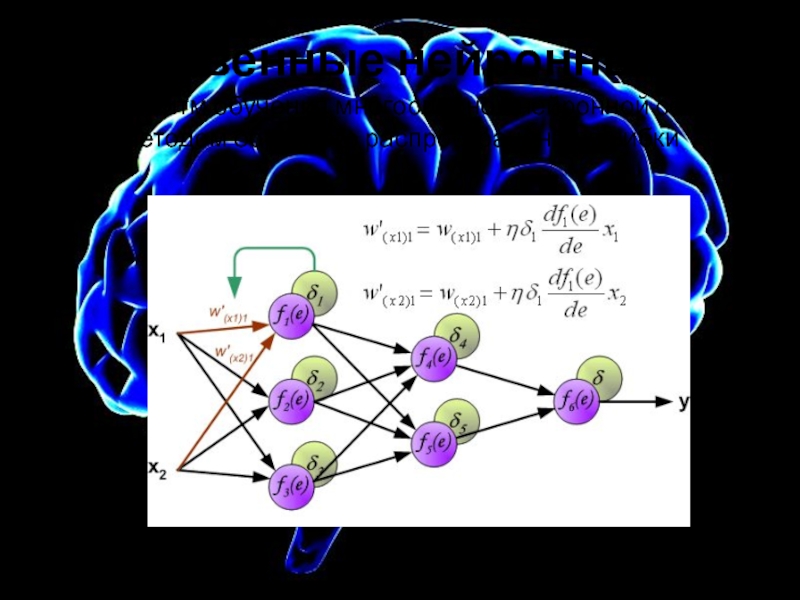
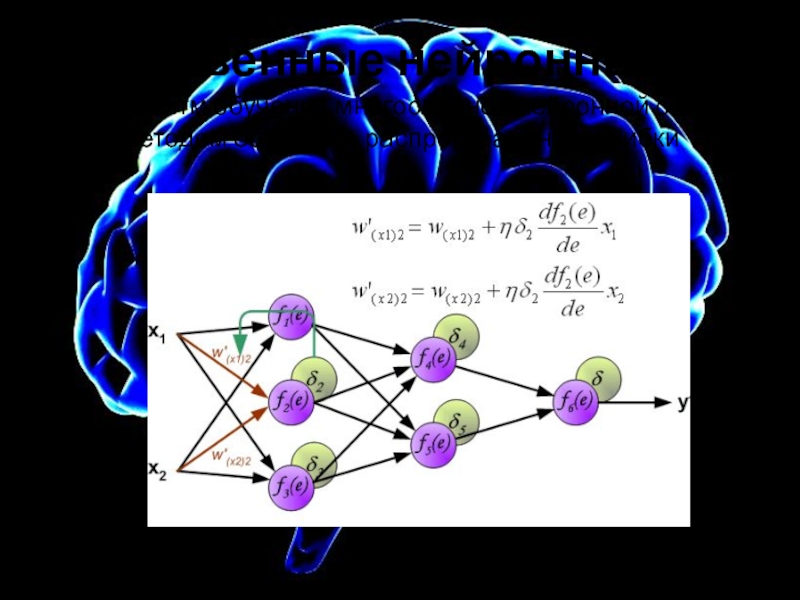
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Слайд 19Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
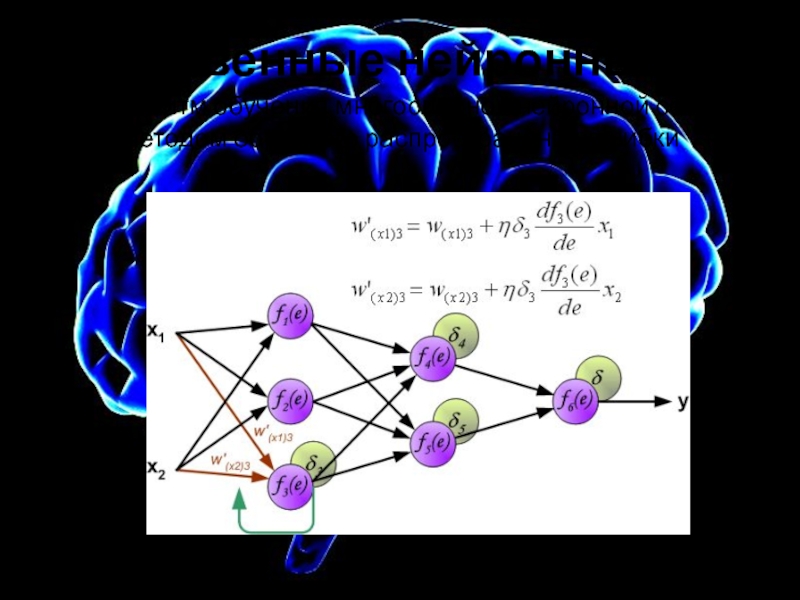
Слайд 20Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
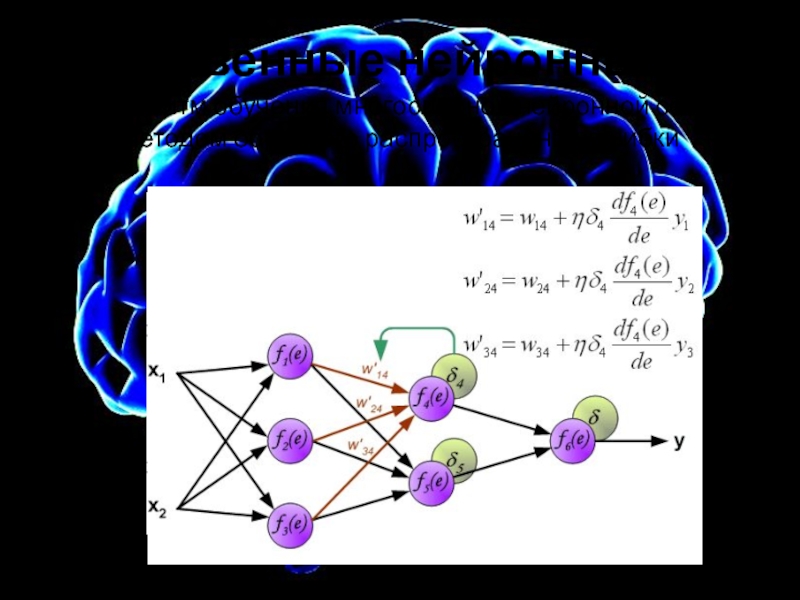
Слайд 21Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
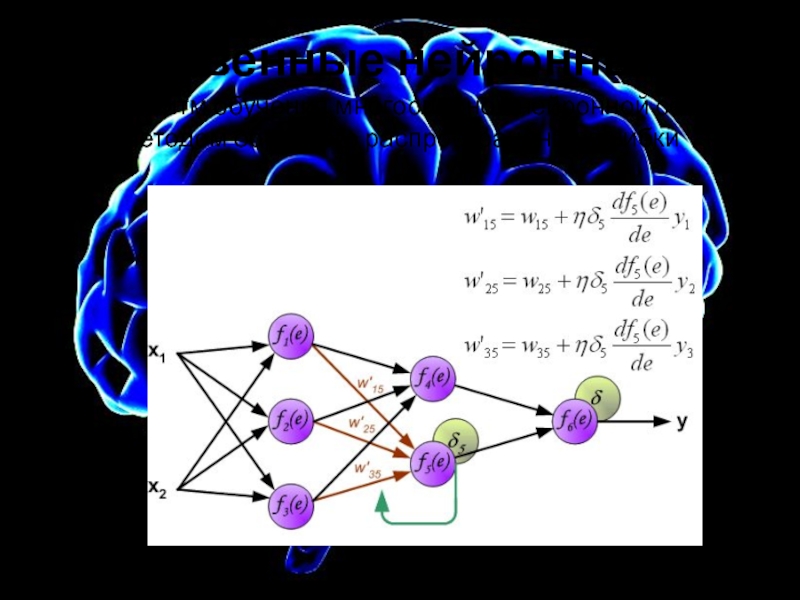
Слайд 22Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Слайд 23Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Слайд 24Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Коэффициент ƞ влияет
Слайд 25Искусственные нейронные сети
Алгоритм обучения многослойной нейронной сети методом обратного распространения ошибки
Слайд 26Искусственные нейронные сети
Обучение “с учителем” и “без учителя”
По принципу обучения нейронных
В первом случае помимо набора входных данных есть соответствующий набор правильных “ответов”, на основании вычисления разница между желаемым ответом и ответом сети и с последующей коррекцией весов построены методы обучения “с учителем”
Во втором случае, есть только набор данных на основании которых сеть должна сделать какие-либо “выводы” (обобщение или кластеризацию)
Метод обратного распространения ошибки в Многослойных персептронах – типичный пример обучения с учителм.
Слайд 27Искусственные нейронные сети
Ограничение на количество синаптических связей
Не смотря на то, что
Для однородный МНС с сигмоидальной активационной функцией существует формула для оценки количества Lw синаптических весов:
mN .
1+log2N
<=
Lw
<=
(N/m+1)(m+n+1)+m
Где n - размерность входного сигнала, m – размерность выходного, N – размерность обучающей выборки. Что для персептрона с одним скрытым слоем даст нейронов. Известны и другие формулы для оценки:
L=
Lw .
n+m
2(n+L+m)<=N<=10(n+L+m) или N/10-n-m<=L<=N/2-n-m



![Искусственные нейронные сетиАлгоритм обучения многослойной нейронной сети методом обратного распространения ошибкиВычисляется значения выходного вектора Y=[y1,y2,y3]](/img/tmb/4/359725/d9dcbab636125fe0bb34b750579a5d40-800x.jpg)
![Искусственные нейронные сетиАлгоритм обучения многослойной нейронной сети методом обратного распространения ошибкиВычисляется значения выходного вектора Y=[y4,y5]](/img/tmb/4/359725/fd6e2a9919aaa5516093029a455d28a8-800x.jpg)