- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физико-химические основы биокатализа в иллюстрациях 4. Ингибирование ферментативных реакций. Методы описания и определения констант ингибирования. Применение элементов теории графов для вывода кинетических уравнений в стационарном режиме презентация
Содержание
- 1. Физико-химические основы биокатализа в иллюстрациях 4. Ингибирование ферментативных реакций. Методы описания и определения констант ингибирования. Применение элементов теории графов для вывода кинетических уравнений в стационарном режиме
- 2. Cкорость ферментативной
- 3. Разрушение фермента Ингибитор Различные факторы (высокие температуры, кислоты) =
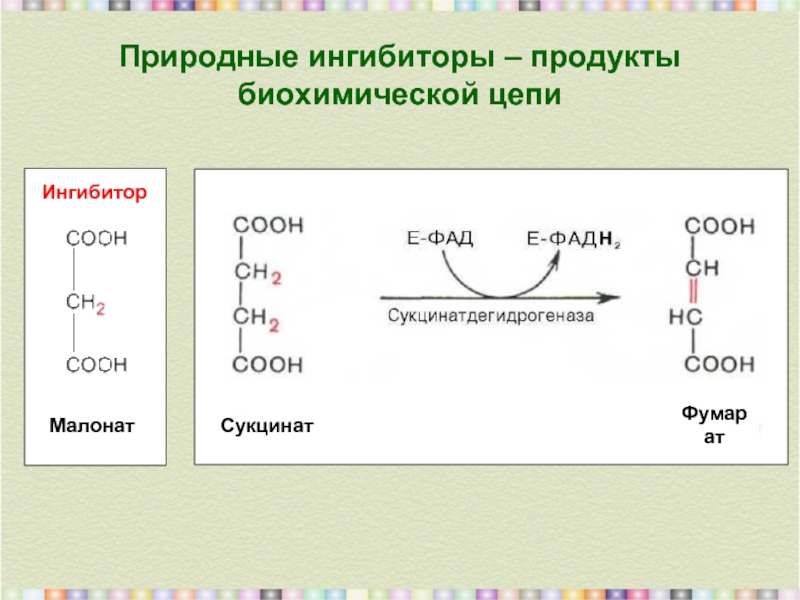
- 4. Природные ингибиторы – продукты биохимической цепи Малонат Сукцинат Фумарат Ингибитор
- 5. Аллостерическое (от греч. "инопространственный") ингибирование В процессе
- 6. Аллостерическое (от греч. "инопространственный") ингибирование Каталитический
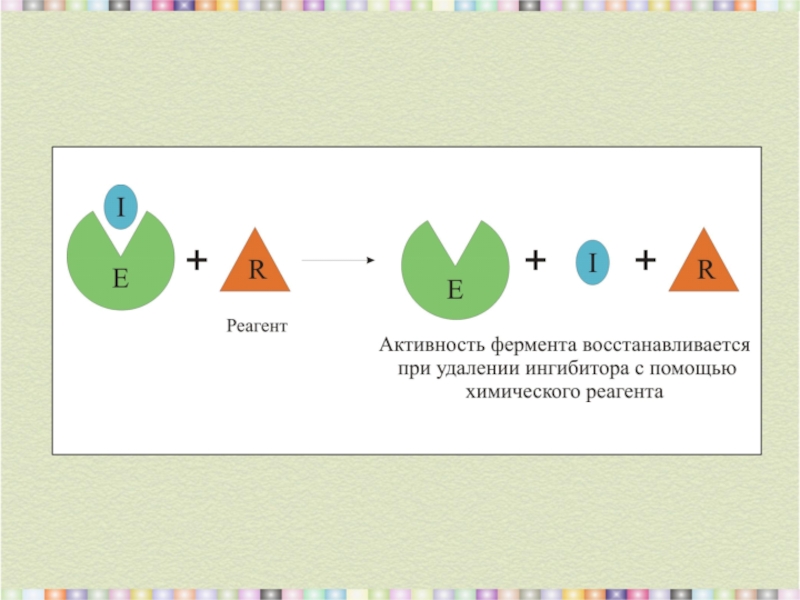
- 7. Связывание ингибитора с ферментом Обратимое Необратимое
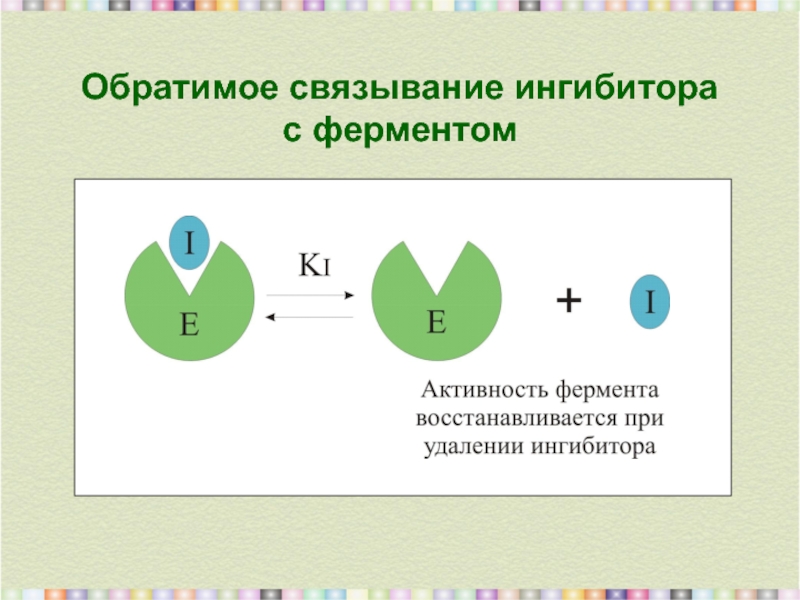
- 8. Обратимое связывание ингибитора с ферментом
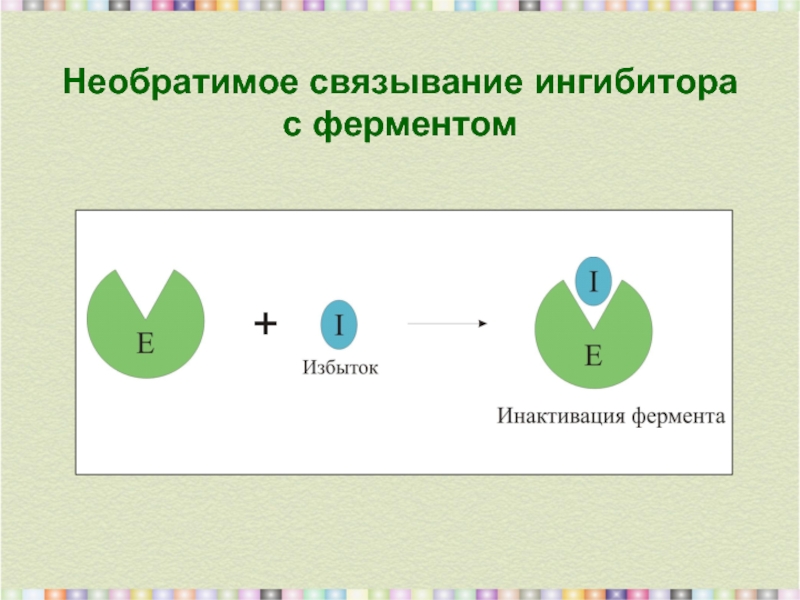
- 9. Необратимое связывание ингибитора с ферментом
- 11. Пример обратимого ингибитора Обратимые ингибиторы, как
- 12. Типы ингибирования 1. Конкурентное ингибирование, 2. Неконкурентное
- 13. Конкурентное ингибирование (δ = γ = 0)
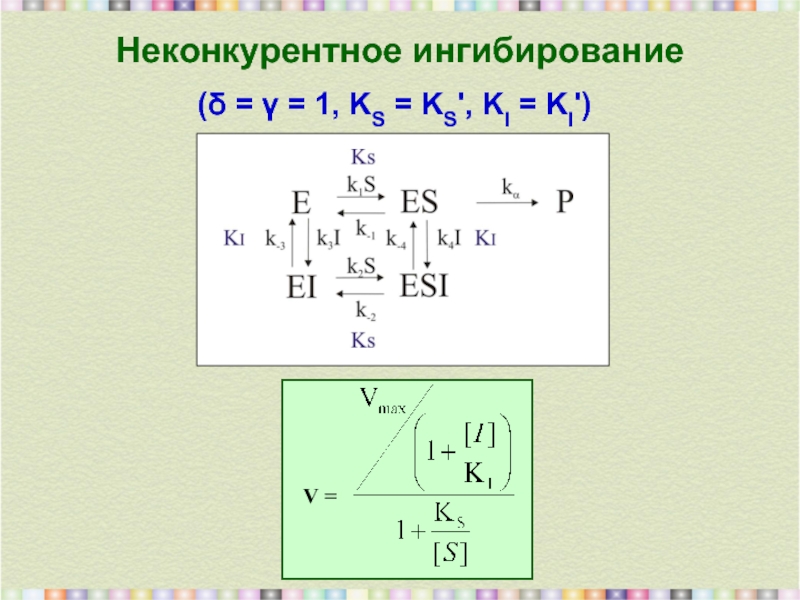
- 14. Неконкурентное ингибирование (δ = γ = 1, KS = KS', KI = KI')
- 15. Смешанное ингибирование (δ = γ ≠ 1, KS ≠ KS', KI ≠ KI')
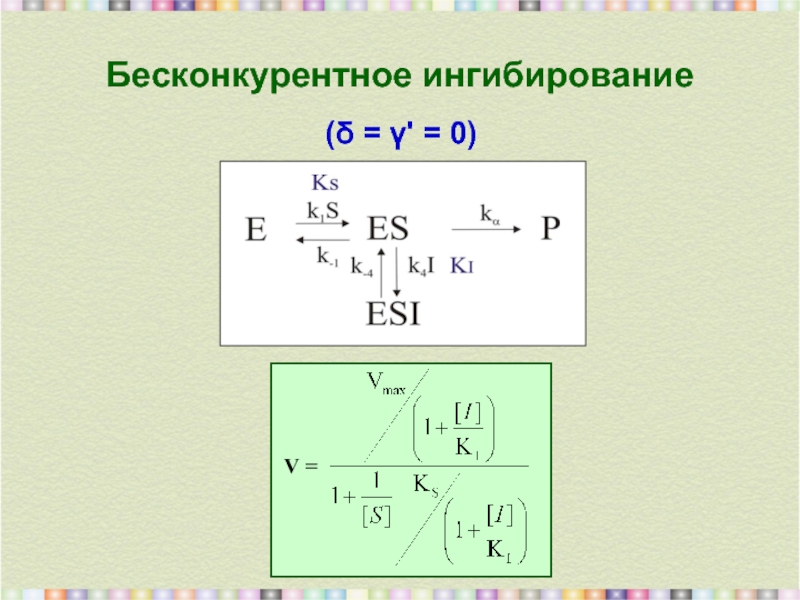
- 16. Бесконкурентное ингибирование (δ = γ' = 0)
- 17. Графические методы определения кинетических параметров реакции в
- 18. Метод Лайнуивера-Берка 1/v (1/[S]) I2 >
- 19. Метод Эди-Хофсти v (v/[S]) I2 >
- 20. Метод Диксона 1/v ([I]) S2 > S1
- 21. Метод Корниш-Боуден [S]/v ([I]) S2 > S1
- 22. Теория графов Граф Эйлера,
- 23. Теория графов Задача: пройти через
- 24. Граф – это схематическое изображение некоторого
- 25. Теория графов. Пример 1: односубстратная
- 26. Теория графов. Пример 2: конкурентное ингибирование
- 27. Теория графов. Пример 3: бесконкурентное ингибирование
Слайд 1Физико-химические основы биокатализа в иллюстрациях 4. Ингибирование ферментативных реакций. Методы описания
Слайд 2
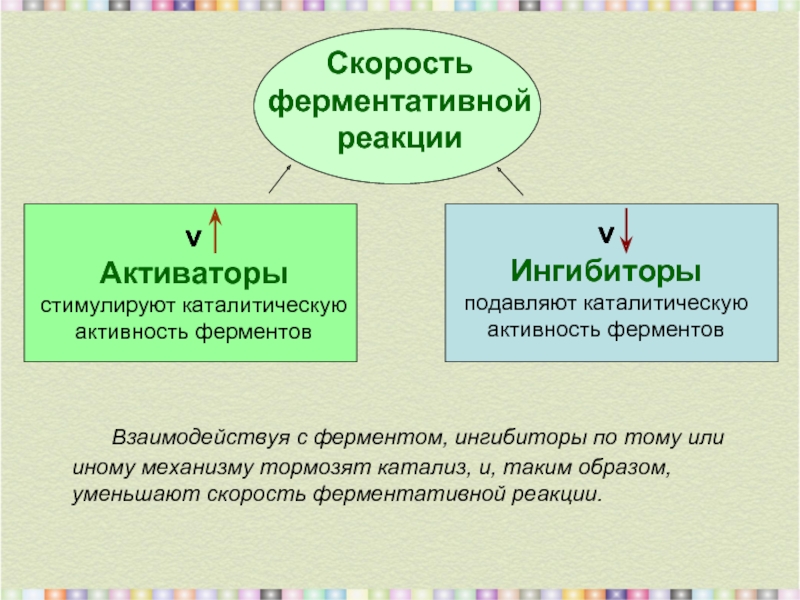
Cкорость
ферментативной
реакции
Взаимодействуя с ферментом, ингибиторы по тому или
v
Активаторы
стимулируют каталитическую
активность ферментов
v
Ингибиторы
подавляют каталитическую
активность ферментов
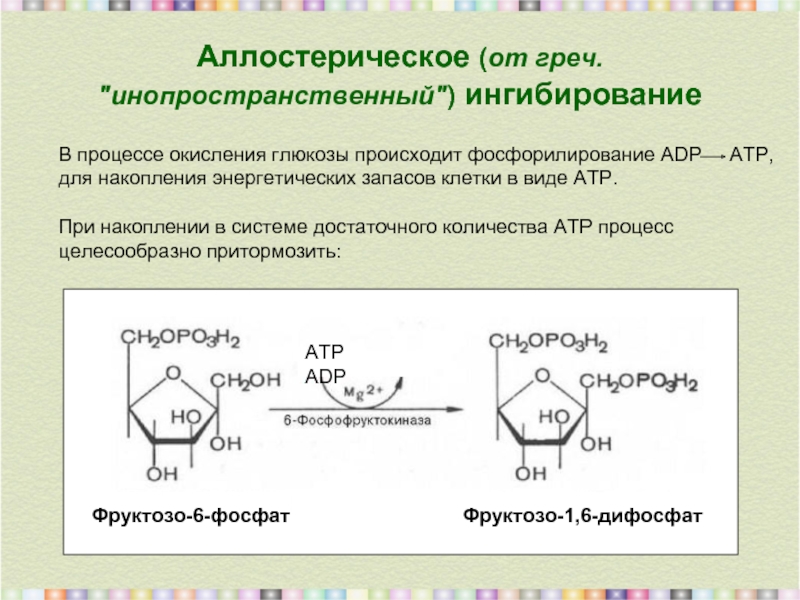
Слайд 5Аллостерическое (от греч. "инопространственный") ингибирование
В процессе окисления глюкозы происходит фосфорилирование АDР
При накоплении в системе достаточного количества АТР процесс целесообразно притормозить:
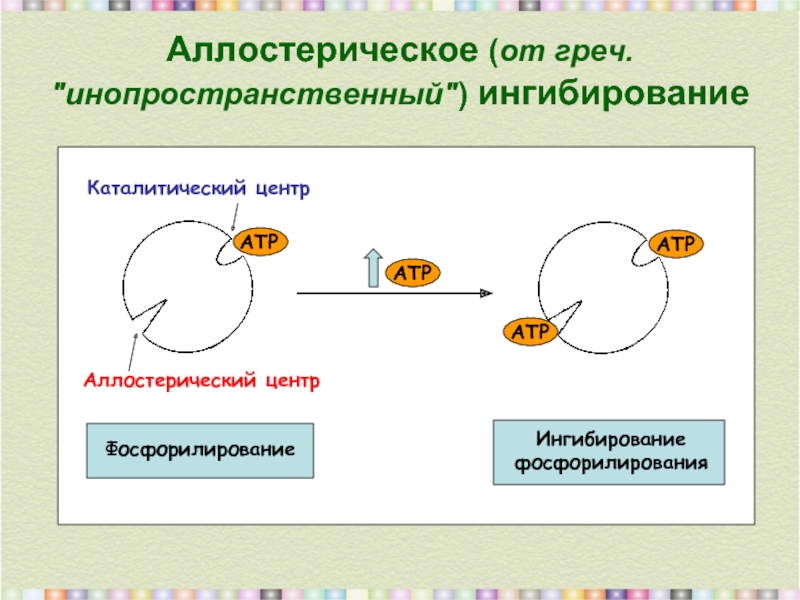
Слайд 6
Аллостерическое (от греч. "инопространственный") ингибирование
Каталитический центр
Аллостерический центр
АТР
АТР
Фосфорилирование
Ингибирование
фосфорилирования
Слайд 11
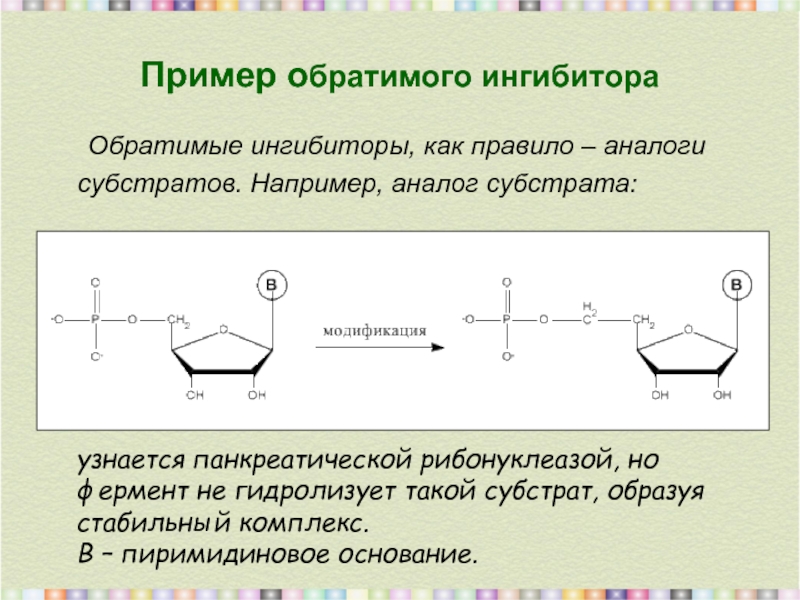
Пример обратимого ингибитора
Обратимые ингибиторы, как правило – аналоги субстратов. Например, аналог
узнается панкреатической рибонуклеазой, но
фермент не гидролизует такой субстрат, образуя
стабильный комплекс.
В – пиримидиновое основание.
Слайд 12
Типы ингибирования
1. Конкурентное ингибирование,
2. Неконкурентное ингибирование,
3. Бесконкурентное ингибирование,
4. Смешанное ингибирование.
k1,,k2,, k3, k4, k-1, k-2, k-3,
KS, KS', KI, KI' – константы диссоциации комплексов фермента с субстратом и/или ингибитором,
γ, γ', δ – численные коэффициенты.
Рассмотрен случай kβ = 0, то есть когда тройной комплекс ESI не
распадается с образованием продукта. При этом скорость реакции
образования продукта равна:
v = kα[ES] (при [S]0, [I]0 >> [E]0).
Слайд 17Графические методы определения кинетических параметров реакции в присутствии ингибитора
На приведенных ниже
V – максимальная скорость реакции,
К – эффективная константа, полученная экспериментально,
KI – константа ингибирования;
а - конкурентное, б - неконкурентное,
в - смешанное, г - бесконкурентное ингибирование.
Слайд 18Метод Лайнуивера-Берка 1/v (1/[S])
I2 > I1, -1/K = -1/KM(1+[I]/KI)
а - конкурентное,
в - смешанное, г - бесконкурентное ингибирование
- I=0
Слайд 19Метод Эди-Хофсти v (v/[S])
I2 > I1, tg α = -K =
а - конкурентное, б - неконкурентное,
в - смешанное, г - бесконкурентное ингибирование
- I=0
Слайд 20Метод Диксона 1/v ([I])
S2 > S1
а - конкурентное, б - неконкурентное,
в - смешанное, г - бесконкурентное ингибирование
Слайд 21Метод Корниш-Боуден [S]/v ([I])
S2 > S1
а - конкурентное, б - неконкурентное,
в - смешанное, г - бесконкурентное ингибирование
Слайд 22
Теория графов
Граф Эйлера, 1736 г.
A
D
B
C
Задача, положившая начало развитию теории графов:
как
Теорема Эйлера: если сеть имеет не более двух «странных»
(с нечетным количеством связей) вершин, есть по крайней
мере один подобный путь.
Леонард Эйлер
1707-1783
Швейцарский и
российский математик
A
B
D
C
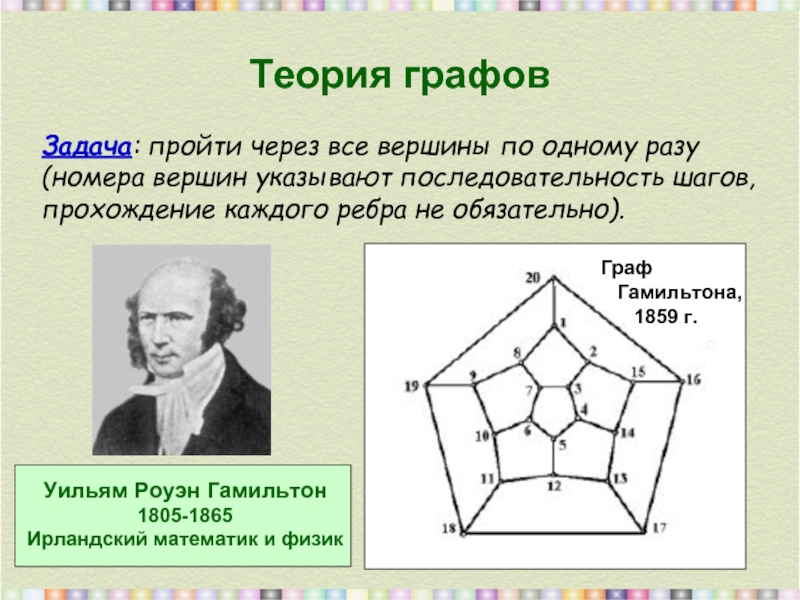
Слайд 23
Теория графов
Задача: пройти через все вершины по одному разу
(номера вершин
прохождение каждого ребра не обязательно).
Граф
Гамильтона,
1859 г.
Уильям Роуэн Гамильтон
1805-1865
Ирландский математик и физик
Слайд 24
Граф – это схематическое изображение некоторого множества элементов и их взаимосвязей.
Ветви графа – линии, соединяющие узлы, имеют направление. Ветвям графа сопоставляются элементарные стадии ферментативной реакции.
Вес ветви – число, характеризующее ветвь графа, эквивалентно константе скорости реакции.
Путь графа – непрерывная совокупность ветвей, в которой ни одна из вершин не встречается более одного раза, не замкнутая (не должно быть циклов).
База – одна из вершин.
Базовое дерево – совокупность ветвей, проходящих через все узлы и ведущих к базе.
Определитель узла (базы) (D) – сумма величин (базовых) деревьев.
Скорость ферментативной реакции можно выразить формулой:
v = E0 , где kr – константа скорости реакции, приводящей к
образованию продукта.
Теория графов
Слайд 25
Теория графов. Пример 1:
односубстратная ферментативная реакция
Граф:
kr = k2
Вес параллельных ветвей,
Dr = DES = k1S
DE = k-1 + k2
v = E0
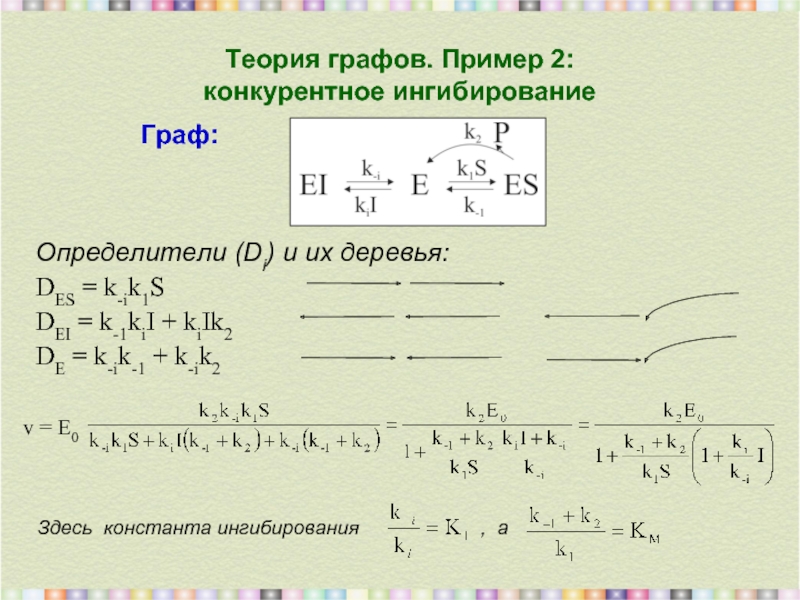
Слайд 26Теория графов. Пример 2:
конкурентное ингибирование
Определители (Di) и их деревья:
DES
DEI = k-1kiI + kiIk2
DE = k-ik-1 + k-ik2
v = E0
Здесь константа ингибирования , а
Слайд 27Теория графов. Пример 3:
бесконкурентное ингибирование
Определители (Di) и их деревья:
DES
DESI = k-1kiI + kiIk2
DE = k-ik-1 + k-ik2
Граф:
v = E0





![Метод Лайнуивера-Берка 1/v (1/[S])I2 > I1, -1/K = -1/KM(1+[I]/KI)а - конкурентное, б - неконкурентное, в](/img/tmb/2/153914/26206e2c7767bb27c4e568dfed64f96c-800x.jpg)
![Метод Эди-Хофсти v (v/[S])I2 > I1, tg α = -K = -KM(1+[I]/KI)а - конкурентное, б](/img/tmb/2/153914/b0432ad89d02a394bb56bb6da217bd5a-800x.jpg)
![Метод Диксона 1/v ([I])S2 > S1а - конкурентное, б - неконкурентное, в - смешанное, г](/img/tmb/2/153914/e6484894b6e42af22fea5182dad6f87d-800x.jpg)
![Метод Корниш-Боуден [S]/v ([I])S2 > S1а - конкурентное, б - неконкурентное, в - смешанное, г](/img/tmb/2/153914/91c22f8626d4c9097c4c9c1bb759c2f7-800x.jpg)