- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дискретные системы и сигналы презентация
Содержание
- 1. Дискретные системы и сигналы
- 2. DSP Z – преобразование Прямое Z –
- 3. DSP Дискретные сигналы и системы
- 4. DSP Дискретные сигналы и системы Прямое
- 5. DSP Дискретные сигналы и системы
- 6. DSP Дискретные сигналы и системы Рассмотрим примеры
- 7. DSP Дискретные сигналы и системы Часто удобно
- 8. DSP Дискретные сигналы и системы Обратное Z
- 9. DSP Дискретные сигналы и системы Для рациональных
- 10. DSP Дискретные сигналы и системы Как
- 11. DSP Дискретные сигналы и системы
- 12. DSP Дискретные сигналы и системы
- 13. DSP Дискретные сигналы и системы Свойства Z
- 14. DSP Дискретные сигналы и системы Для одностороннего
- 15. DSP Дискретные сигналы и системы 3).
- 16. DSP Дискретные сигналы и системы 4).Перемножение последовательностей.
- 17. DSP Дискретные сигналы и системы Таблица 1.
- 18. DSP Дискретные сигналы и системы Таблица
- 19. DSP Дискретные сигналы и системы Решение разностных
- 20. DSP Дискретные сигналы и системы Воспользуемся свойством
- 21. DSP Дискретные сигналы и системы Первая компонента
- 22. DSP Дискретные сигналы и системы Передаточная (системная)
- 23. DSP Дискретные сигналы и системы Часто z-преобразование
- 24. DSP Дискретные сигналы и системы Если систему
- 25. DSP Дискретные сигналы и системы Эта формула
- 26. DSP Дискретные сигналы и системы Если система
- 27. DSP Дискретные сигналы и системы Одним из
- 28. DSP Дискретные сигналы и системы Чтобы определить
- 29. DSP Дискретные сигналы и системы Рисунок 3.
- 30. DSP Дискретные сигналы и системы Для определения
- 31. DSP Дискретные сигналы и системы В качестве
- 32. DSP Дискретные сигналы и системы Рисунок
Слайд 2DSP
Z – преобразование
Прямое Z – преобразование
Обратное Z – преобразование
Свойства
Решение разностных уравнений с применением Z – преобразования
Передаточная (системная) функция
Слайд 3DSP
Дискретные сигналы и системы
Z – преобразование
В теории систем непрерывного
Слайд 4DSP
Дискретные сигналы и системы
Прямое Z – преобразование
Для последовательности x(n), заданной
(2.1)
где z - комплексная переменная. Если представить комплексную переменную z в показательной форме z=rejω, то (2.1) можно интерпретировать как ДВПФ :
(2.2)
Действительно, согласно (2.2) z–преобразование x(n) можно интерпретировать как ДВПФ последовательности x(n), умноженной на экспоненциальную последовательность r -n. Очевидно, что для |z| = r = 1, т.е. на окружности единичного радиуса в комплексной z-плоскости, z–преобразование x(n) совпадает с ДВПФ последовательности x(n).
Слайд 5DSP
Дискретные сигналы и системы
Соотношение (2.1) называют двусторонним z–преобразованием, а в большинстве
(2.3)
При x(n)=0, для n<0, т.е. для физически реализуемых последовательностей эти преобразования эквивалентны.
Для любой последовательности множество тех значений z, для которых z–преобразование сходится (|Χ(z)|<∞), называется областью сходимости. Ряд (2.1) сходится, если выполняется соотношение
(2.4)
следующее из условия сходимости ДВПФ.
Для последовательностей, растущих не быстрее, чем экспонента, z–преобразование будет сходиться для всех z , находящихся вне некоторого круга в комплексной z-плоскости, радиус r0 которого называют радиусом сходимости. Соответствие между x(n) и X(z) взаимно однозначное т.е. каждому x(n) соответствует только одно X(z) , определенное для |z|>r0 и обратно.
Слайд 6DSP
Дискретные сигналы и системы
Рассмотрим примеры нахождения z–преобразований некоторых полезных последовательностей.
1).
2). Найдем z–преобразование единичной ступенчатой последовательности x(n)=u(n).
Поскольку x(n)=0 везде, кроме n≥ 0, где x(n)=1, то
причем X(z) сходится при |z| >1 , так как X(z) имеет единственную особую точку (полюс) z =1, в которой X(1)=∞.
3). Найдем z–преобразование действительной экспоненциальной последовательности x(n)=аnu(n). Получим
X(z) сходится при |z|>а , так как X(z) имеет единственную особую точку (полюс) z =a.
4). Найдем z–преобразование комплексной экспоненциальной последовательности x(n)=ejωn u(n). Получим
X(z) сходится при |z|>1, так как X(z) имеет единственную особую точку (полюс) z = ejω
Слайд 7DSP
Дискретные сигналы и системы
Часто удобно изображать z–преобразование графически с помощью диаграммы
а полюсы - это корни полинома знаменателя, при которых X(z)=∞. Так, для X(z), полученного в примере 4, нуль соответствует z = 0, а полюс z = ejω.
На рис.1 нуль обозначен кружком, полюс крестиком, а область сходимости обозначена штриховкой и включает все z на плоскости, удовлетворяющие условию |z|>1.
Рисунок 1.
Слайд 8DSP
Дискретные сигналы и системы
Обратное Z – преобразование
Обратный переход от z–преобразования
(2.5)
Это обратное z–преобразование содержит интеграл по любому замкнутому контуру с направлением обхода против часовой стрелки, расположенному в области сходимости и окружающему начало координат.
При выводе соотношения (2.5) используется теорема Коши, согласно которой
(2.6)
Умножая (2.1) на zk-1 и интегрируя по замкнутому контуру, окружающему начало координат, получим
откуда следует (2.5).
Слайд 9DSP
Дискретные сигналы и системы
Для рациональных z–преобразований контурные интегралы вида (2.5) удобно
(2.7)
когда X(z)zn-1 имеет полюс порядка s в точке z=pi, ψ(z) не имеет полюсов в z=pi . Вычет X(z)zn-1 в точке z=pi определяется формулой
В частности, если pi – полюс первого порядка, то
Слайд 10DSP
Дискретные сигналы и системы
Как пример рассмотрим вычисление обратного преобразования от
|z|>а. Используя (2.7), получим
где контур интегрирования С является окружностью с радиусом больше а. Тогда при n≥ 0 контур интегрирования содержит только один полюс первого порядка в точке z=a. Следовательно, при n ≥ 0 x(n) = an . При n<0 в точке z=0 имеется кратный полюс, порядок которого зависит от n. При n=-1 этот полюс имеет первый порядок с вычетом, равным (–a-1). Вычет в полюсе z=a равен a-1. Следовательно, сумма вычетов равна нулю и поэтому x(-1)=0. Продолжая эту процедуру, можно проверить, что в этом примере x(n) =0 при n<0. Поэтому x(n)=аnu(n) для всех n.
Слайд 11DSP
Дискретные сигналы и системы
Во многих случаях вычисления по формуле (2.7) оказываются
1). Разложение на простые дроби.
Например, для рационального z–преобразования с однократными полюсами X(z) можно представить в форме суммы простых дробей
тогда
для всех n.
Слайд 12DSP
Дискретные сигналы и системы
2). Разложение в степенной ряд.
Если z–преобразование имеет вид
Если X(z) дается в замкнутом виде, то часто можно вывести соответствующий степенной ряд или использовать известное разложение в ряд. Например, для
|z|>а представление в виде степенного ряда можно получить непосредственным делением числителя z на знаменатель z-a:
Слайд 13DSP
Дискретные сигналы и системы
Свойства Z – преобразования
Рассмотрим некоторые наиболее важные
1). Линейность.
z–преобразование есть линейное преобразование, что означает справедливость для него принципа суперпозиции. Если z–преобразования последовательностей y(n), x1(n), x2(n) равны Y(z), X1(z), и X2(z) соответственно, то для любых действительных a и b справедливы соотношения: для y(n)=ax1(n)+bx2(n), Y(z)=aX1(z)+bX2(z).
2). Сдвиг последовательности (задержка).
Если z–преобразования последовательностей y(n), x(n) равны Y(z), X(z) соответственно, то для y(n)=x(n-n0), где n0-целое число, справедливо соотношение:
(2.8)
Так, при задержке на один такт y(n)=x(n-1), Y(z)=z-1X(z) т.е.
z–преобразование исходной последовательности умножается на z-1. Поэтому иногда пользуются оператором задержки на такт
z-1{}, понимая под ним следующее соотношение: z-1{x(n)}=x(n-1).
Слайд 14DSP
Дискретные сигналы и системы
Для одностороннего z–преобразования свойство задержки следует рассмотреть подробнее.
то
Если x(n)=0 при n<0, то , т.е свойство задержки физически реализуемых последовательностей сохраняется и для одностороннего z–преобразования.
(2.9)
Однако для опережающего сдвига физически реализуемой последовательности, т.е. для случая, когда y(n)=x(n+n0), (n0>0 и целое), аналогично (2.9) легко получить соотношение:
Соотношения (2.8) и (2.9) используются при решении разностных уравнений с применением одностороннего z–преобразования.
(2.10)
Слайд 15DSP
Дискретные сигналы и системы
3). Свертка последовательностей.
Пусть
Если z–преобразования последовательностей y(n), x(n),
Y(z)=X(z)H(z),
которое означает, что z–преобразование свертки равно произведению z–преобразований свертываемых последовательностей. Действительно,
(2.11)
Слайд 16DSP
Дискретные сигналы и системы
4).Перемножение последовательностей.
Пусть y(n)=x1(n)x2(n). Если z–преобразования последовательностей y(n), x1(n),
Это соотношение называют комплексной сверткой. При z=ejω и v=ejθ из (2.12) имеем
Следовательно, ДВПФ произведения последовательностей есть периодическая (круговая) свертка ДВПФ сомножителей.
Доказательство (2.12):
(2.12)
(2.12а)
Важным следствием (2.12a) является равенство Парсеваля:
(2.13)
Слайд 18DSP
Дискретные сигналы и системы
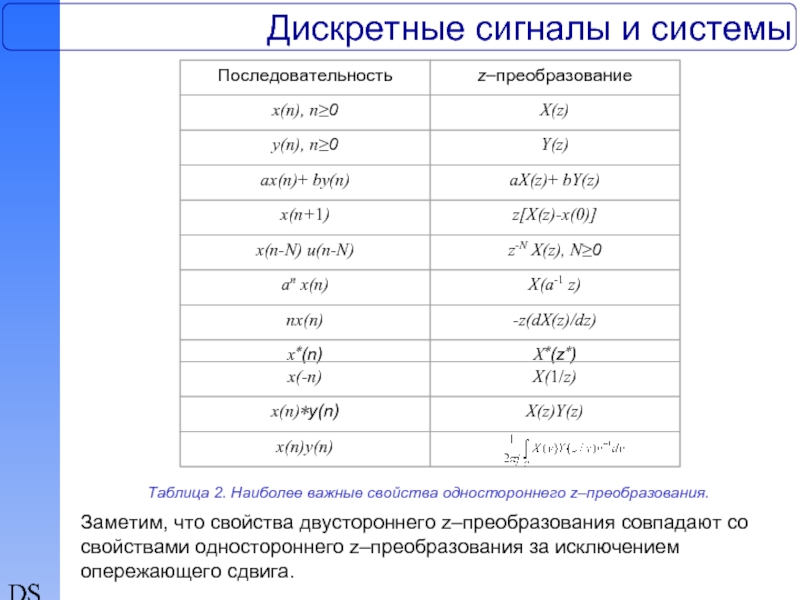
Таблица 2. Наиболее важные свойства одностороннего z–преобразования.
Заметим, что
Слайд 19DSP
Дискретные сигналы и системы
Решение разностных уравнений с применением z-преобразования
Разностные уравнения
с начальным условием y(-1)=k. Пусть входной сигнал есть экспоненциальная последовательность . Найдем одностороннее z–преобразование обеих частей уравнения:
Слайд 20DSP
Дискретные сигналы и системы
Воспользуемся свойством (2.9), связанным с задержкой последовательности, получим:
откуда
Поскольку для , , то
Разлагая второе слагаемое на простые дроби, получим
Находя обратное z–преобразование, получим
Слайд 21DSP
Дискретные сигналы и системы
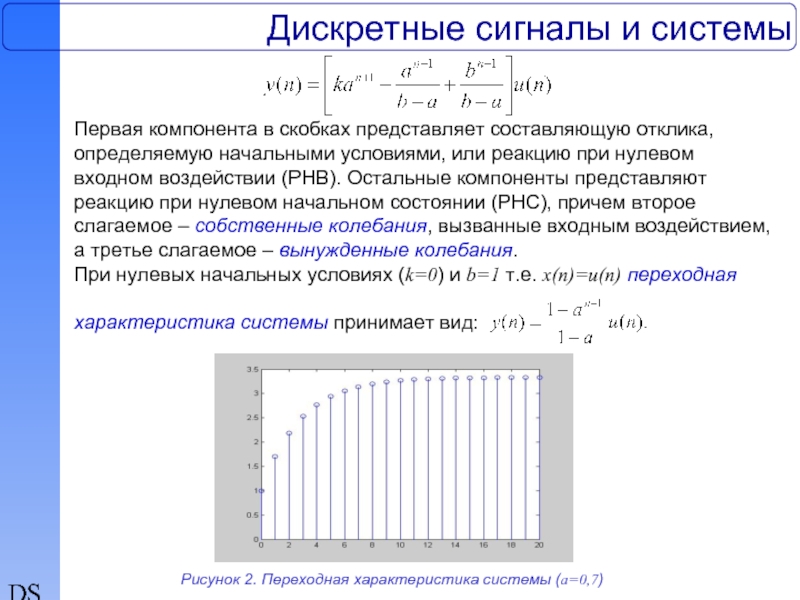
Первая компонента в скобках представляет составляющую отклика, определяемую
При нулевых начальных условиях (k=0) и b=1 т.е. x(n)=u(n) переходная
характеристика системы принимает вид:
Рисунок 2. Переходная характеристика системы (а=0,7)
Слайд 22DSP
Дискретные сигналы и системы
Передаточная (системная) функция
Выше мы рассмотрели описание линейных
Более общим образом можно описать линейные с постоянными параметрами системы с помощью z-преобразования импульсной характеристики. Обозначая х(п), у(п) и h(n) вход, выход и импульсную характеристику соответственно и X(z), Y(z) и H(z) их z-преобразования и используя результаты предыдущего раздела, получим из свертки у(п) = х(п) * h(п) соотношение
Y(z)=X(z)H(z). (2.14)
Как и в случае преобразования Фурье, соотношение между входом и выходом для линейных с постоянными параметрами систем получается умножением z-преобразований входного сигнала и импульсной характеристики.
Слайд 23DSP
Дискретные сигналы и системы
Часто z-преобразование импульсной характеристики называется передаточной или системной
Было показано, что необходимым и достаточным условием устойчивости системы является абсолютная суммируемость импульсной характеристики h(п). Область сходимости z-преобразования импульсной характеристики h(п) определяется теми значениями z, при которых h(n)z-n — абсолютно суммируемая последовательность. Поэтому, если область сходимости передаточной функции включает единичную окружность, система устойчива и наоборот. Кроме того, мы можем утверждать, что для устойчивой и физически реализуемой системы: область сходимости будет, включать единичную окружность и всю z-плоскость вне единичной окружности, включая z=∞.
Слайд 24DSP
Дискретные сигналы и системы
Если систему можно описать линейным разностным уравнением с
Применяя z-преобразование к обеим частям разностного уравнения с учетом свойства линейности и свойства задержки, получим
Поэтому
(2.15)
Слайд 25DSP
Дискретные сигналы и системы
Эта формула дает конкретное выражение для передаточной функции,
Так как выражение (2.15) есть отношение полиномов от z-1, то его можно записать в виде
(2.15)
(2.16)
Каждый из сомножителей (1—ziz-1) в числителе (2.16) дает нуль при z =zi и полюс при z=0. Аналогично каждый сомножитель вида (1— piz-1) в знаменателе дает полюс при z=pi и нуль в начале координат. То, что передаточная функция системы равна отношению полиномов от z-1 является характерной чертой систем, описываемых линейными разностными уравнениями с постоянными коэффициентами. Следовательно, с точностью до скалярного множителя А в (2.16) передаточная функция может быть полностью описана картиной полюсов и нулей в z-плоскости.
(2.16)
Слайд 26DSP
Дискретные сигналы и системы
Если система устойчива, то все полюсы должны лежать
Пример.
В качестве простого примера рассмотрим физически реализуемую систему, описываемую разностным уравнением у(п) = ау(п-1)+х(п). Передаточная функция равна
и в силу предположения о физической реализуемости область сходимости определяется неравенством |z|>|a|, откуда следует, что импульсная характеристика равна h(п )=апи(п).
В частном случае, когда N=0 в (2.15) или (2.16), система не имеет полюсов, за исключением точки z=0, и ее импульсная характеристика имеет конечную длительность. При N>0 система имеет полюсы, каждый из которых прибавляет экспоненциальную последовательность к импульсной характеристике. Таким образом, если передаточная функция имеет полюсы, то импульсная характеристика имеет бесконечную протяженность.
Слайд 27DSP
Дискретные сигналы и системы
Одним из преимуществ представления передаточной функции посредством ее
Слайд 28DSP
Дискретные сигналы и системы
Чтобы определить передаточную функцию на единичной окружности, нужно
Представляя H(ejω) = | H(ejω) |ejarg[H(.)], получим
(2.17)
(2.18)
Слайд 29DSP
Дискретные сигналы и системы
Рисунок 3. Геометрическая интерпретация измерения
Геометрическая интерпретация соотношений (2.17) — (2.18) дана на рис.3. Из точки z = ejω находящейся на единичной окружности, во все нули и полюсы проведены векторы. По их величине определяется модуль передаточной функции на заданной частоте ω, а по их углам — фаза. В примере на рис.3 имеются три полюса (N = 3) и два нуля (М = 2), а коэффициент А =1, поэтому (рис.3)
Слайд 30DSP
Дискретные сигналы и системы
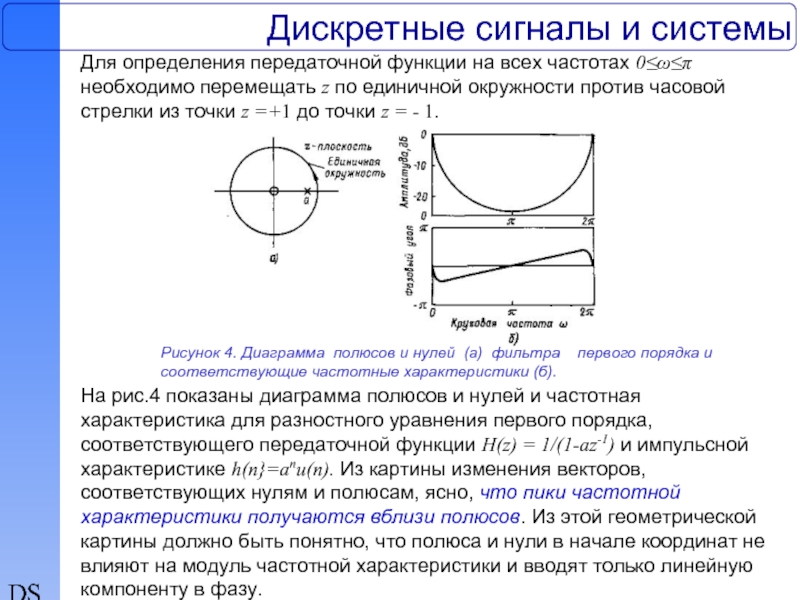
Для определения передаточной функции на всех частотах 0≤ω≤π
Рисунок 4. Диаграмма полюсов и нулей (а) фильтра первого порядка и соответствующие частотные характеристики (б).
На рис.4 показаны диаграмма полюсов и нулей и частотная характеристика для разностного уравнения первого порядка, соответствующего передаточной функции H(z) = 1/(1-az-1) и импульсной характеристике h(n}=anu(n). Из картины изменения векторов, соответствующих нулям и полюсам, ясно, что пики частотной характеристики получаются вблизи полюсов. Из этой геометрической картины должно быть понятно, что полюса и нули в начале координат не влияют на модуль частотной характеристики и вводят только линейную компоненту в фазу.
Слайд 31DSP
Дискретные сигналы и системы
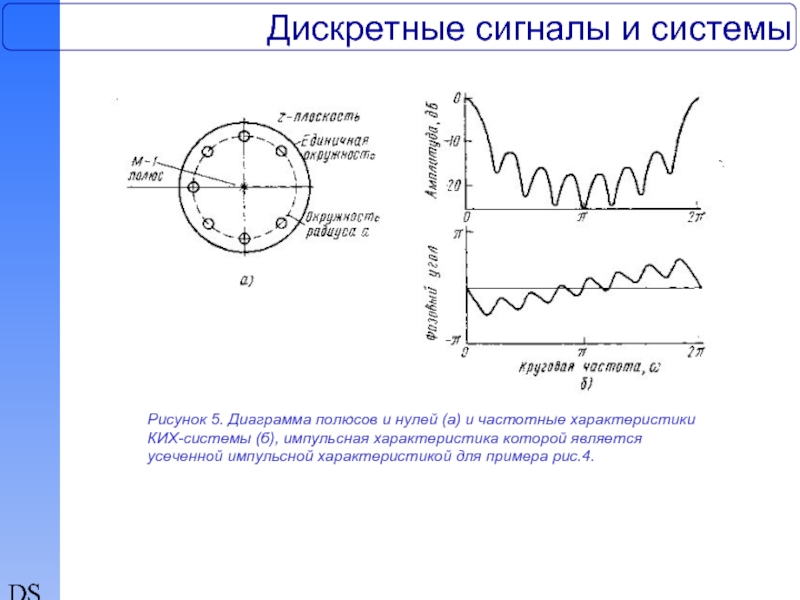
В качестве второго примера рассмотрим случай, когда импульсная
Тогда передаточная функция равна
или H(z) = (zM-aM)/zM-1(z-а). Так как числитель имеет нули при zk=aej(2π/M)k, k=0,1,…,M-1, где а считается положительным числом, то полюс при z=a компенсируется нулем в той же точке. Диаграмма полюсов и нулей и соответствующая частотная характеристика для случая М=8 показана на рис. 5. Заметим наличие пика при ω=0 (z=1), где нет нулей, и провалов в частотной характеристике в окрестности каждого нуля. Эти свойства частотной характеристики легко выводятся геометрически из диаграммы полюсов и нулей.