- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы решения оптимизационных задач презентация
Содержание
- 1. Численные методы решения оптимизационных задач
- 2. План лекции Постановка и виды задач оптимизации
- 3. Постановка задачи оптимизации Экстремум берется относительно порядка заданного на Y
- 4. Классификация по структуре допустимого множества
- 5. Классификация по числу критериев Скалярная оптимизация (один
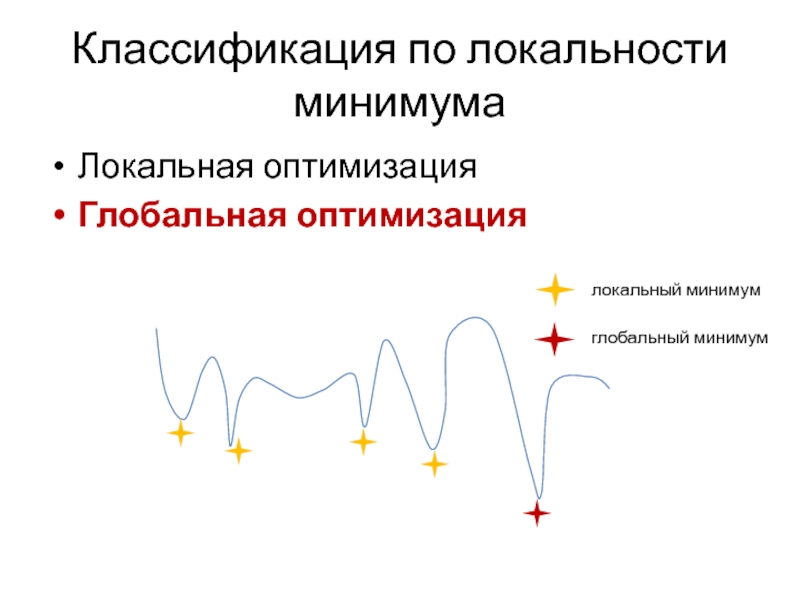
- 6. Классификация по локальности минимума Локальная оптимизация Глобальная оптимизация
- 7. Классификация по гарантии оптимальности Эвристические методы (не
- 8. Примеры задач глобальной оптимизации оптимизация инвестиционного
- 9. Метод Неравномерных Покрытий Предложен Ю.Г. Евтушенко в
- 10. Метод неравномерных покрытий Предложен для безусловной оптимизации
- 11. Безусловная оптимизация: постановка задачи Требуется найти точку
- 12. Упрощение постановки От безусловной переходим к оптимизации
- 13. Метод неравномерных покрытий для одномерной безусловной оптимизации
- 14. Метод неравномерных покрытий для одномерной безусловной оптимизации [ a ] b
- 15. Общий случай: основная теорема L2 L3 L4
- 16. Основные составляющие МНП Построение покрытия (системы покрывающих множеств) Построение последовательности рекордных точек
- 17. Липшицева Миноранта 1-го порядка Условие Липшица: Миноранта:
- 18. Липшицева миноранта 2-го порядка Градиент удовлетворяет условию
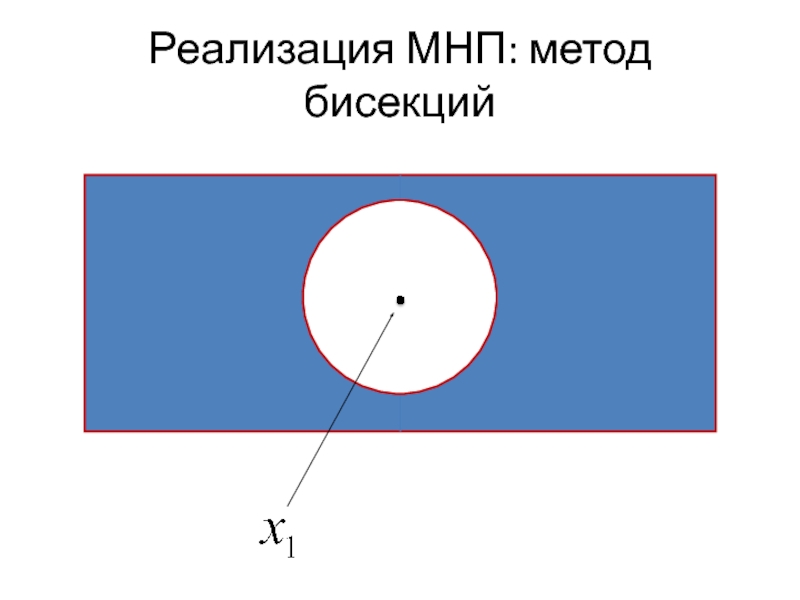
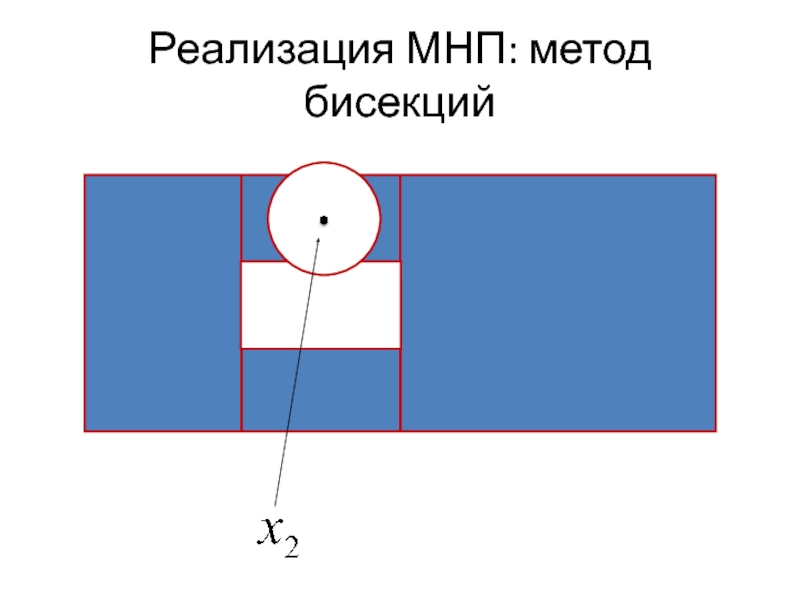
- 19. Реализация МНП: метод бисекций
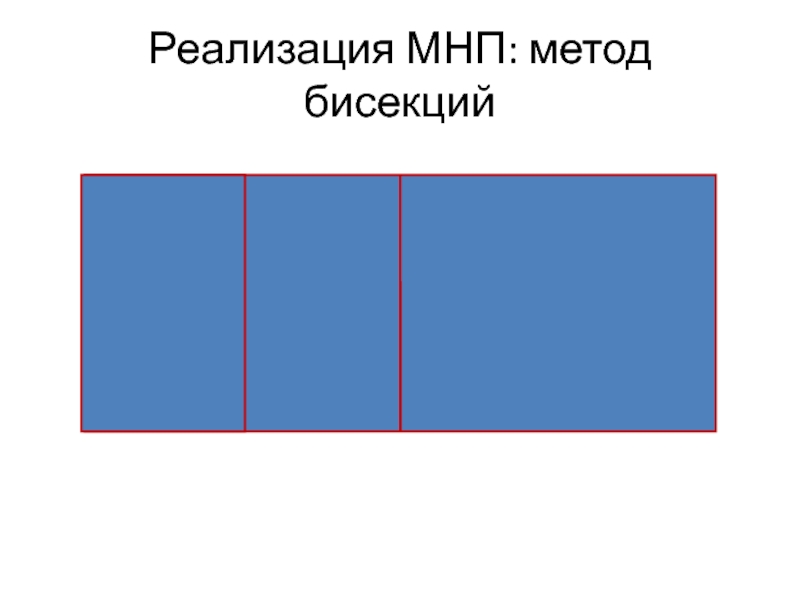
- 20. Реализация МНП: метод бисекций
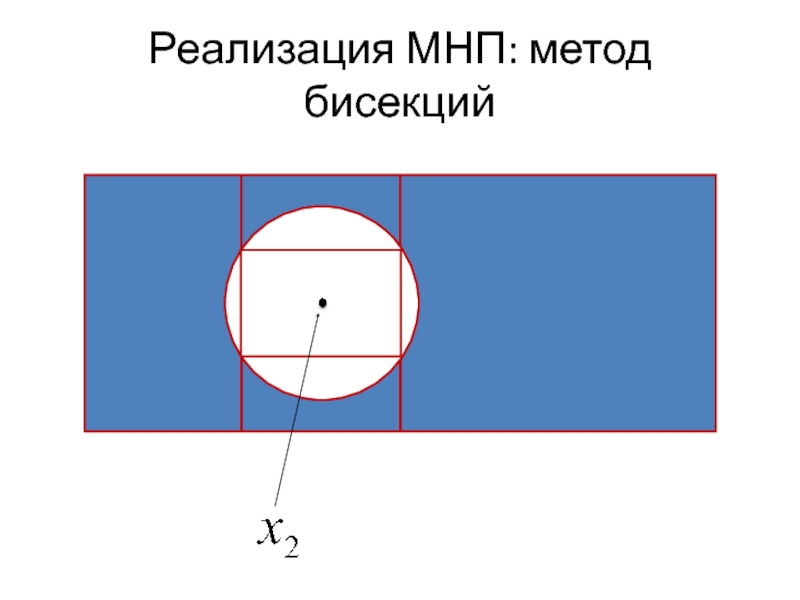
- 21. Реализация МНП: метод бисекций
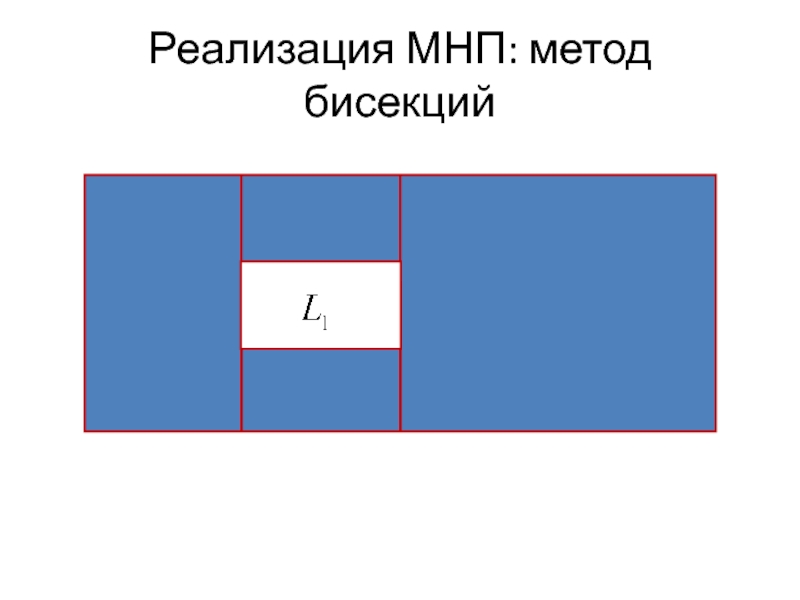
- 22. Реализация МНП: метод бисекций
- 23. Реализация МНП: метод бисекций
- 24. Реализация МНП: метод бисекций
- 25. Реализация МНП: метод бисекций
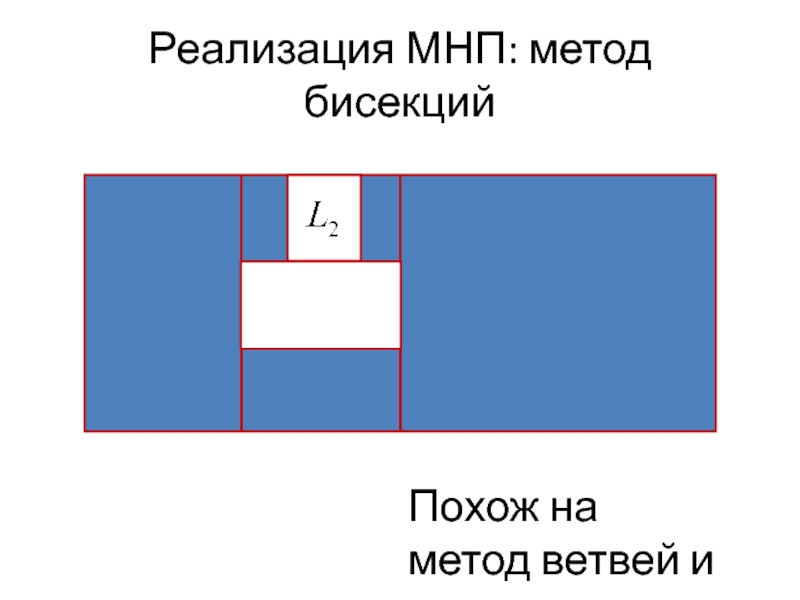
- 26. Реализация МНП: метод бисекций Похож на метод ветвей и границ
- 28. Нахождение хорошего рекорда Использование локальных и эвристических
- 29. Задачи с ограничениями: постановка непрерывные Найти:
- 30. МНП для задач с ограничениями Допустимая область
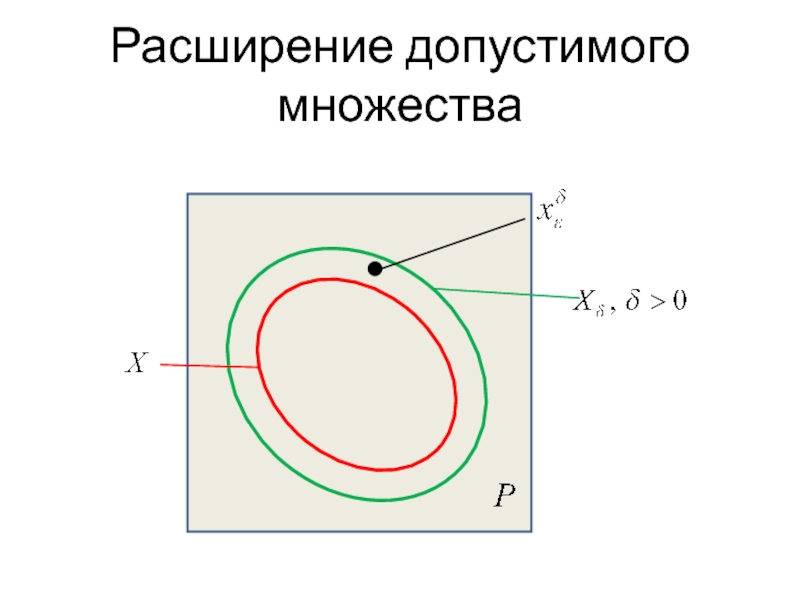
- 31. Расширение допустимого множества
- 32. Оптимизация с ограничениями: основная идея Если
- 33. Оптимизация с ограничениями: основная теорема L2 L3
- 34. Учет целочисленности Множество, исключаемое из рассмотрения, расширяется до целочисленных границ
- 35. Частично целочисленные задачи Требуется минимизировать затраты f(x) на производство при соблюдении технологических ограничений g1-g4.
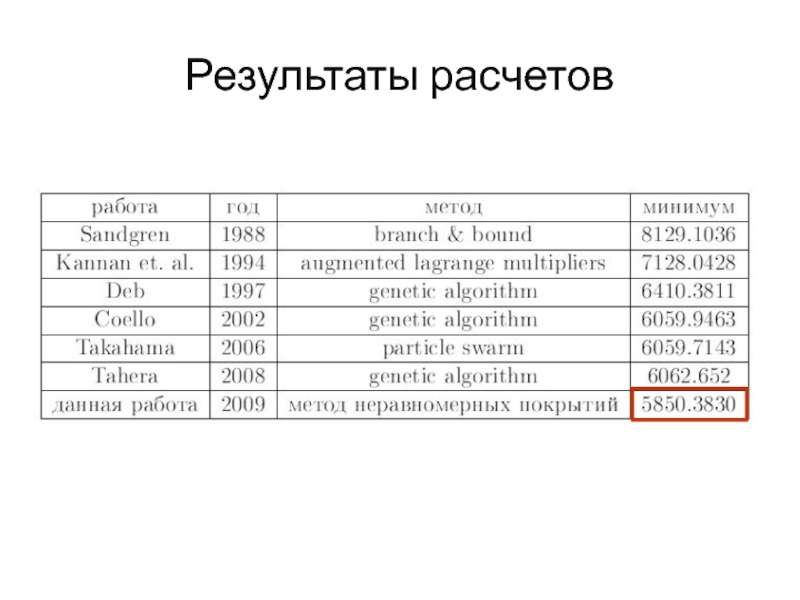
- 36. Результаты расчетов
- 37. Метод ветвей и границ
- 38. Проблемы распараллеливания МВГ дерево ветвления не является
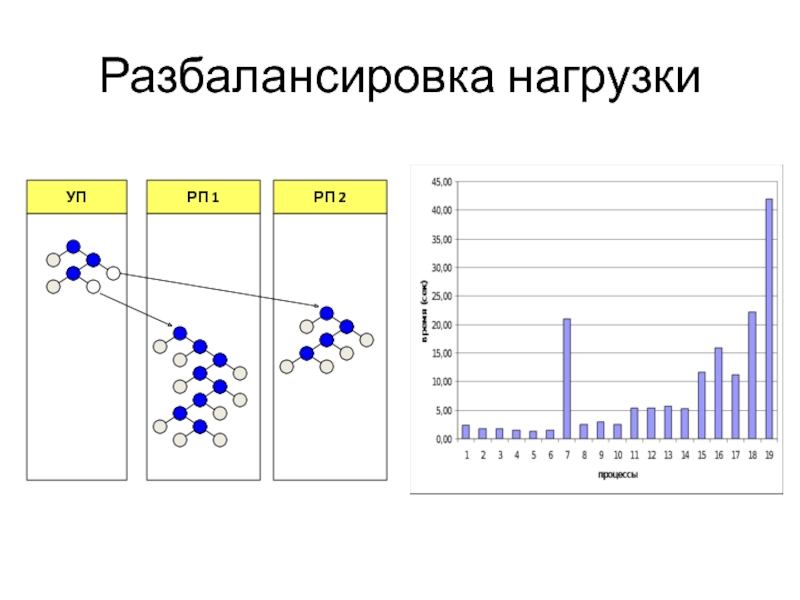
- 39. Разбалансировка нагрузки
- 40. Разделение проблемно-зависимых и независимых частей
- 41. Реализация для различных архитектур: повторное использование многопроцессорные
- 42. Структура пакета BNB-Solver (С ++) БАЗОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ
- 43. Проблема балансировки нагрузки Число вершин в разных
- 44. Адаптивная балансировка нагрузки РП выполняет Tb
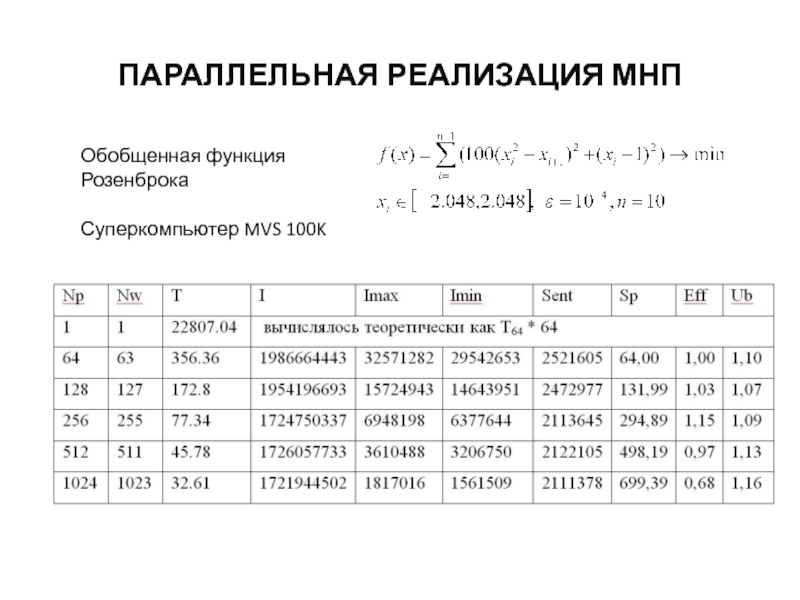
- 45. ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ МНП Обобщенная функция Розенброка Суперкомпьютер MVS 100K
- 46. Современные проблемы МНП Усовершенствование метода Новые способы
- 47. Проблемы эффективной реализации Преодоление 100 TFLOPS: совершенствование
- 48. Спасибо за внимание!
Слайд 1Численные методы решения оптимизационных задач
Ю.Г. Евтушенко, М.А. Посыпкин
Вычислительный центр РАН
Слайд 2План лекции
Постановка и виды задач оптимизации
Метод неравномерных покрытий (МНП)
Безусловная оптимизация
Математическое
Эффективная реализация МНП на современных архитектурах
Слайд 4Классификация по структуре допустимого множества
- дискретная оптимизация
математическое программирование
Линейное программирование
Нелинейное программирование
частично-целочисленное программирование (оптимизация)
Слайд 5Классификация по числу критериев
Скалярная оптимизация (один критерий)
Многокритериальная оптимизация (более одного критерия)
Слайд 7Классификация по гарантии оптимальности
Эвристические методы (не дают информацию о точности найденного
Детерминированные методы (гарантируют оптимальность с заданной точностью)
Оптимум
Приближенное решение
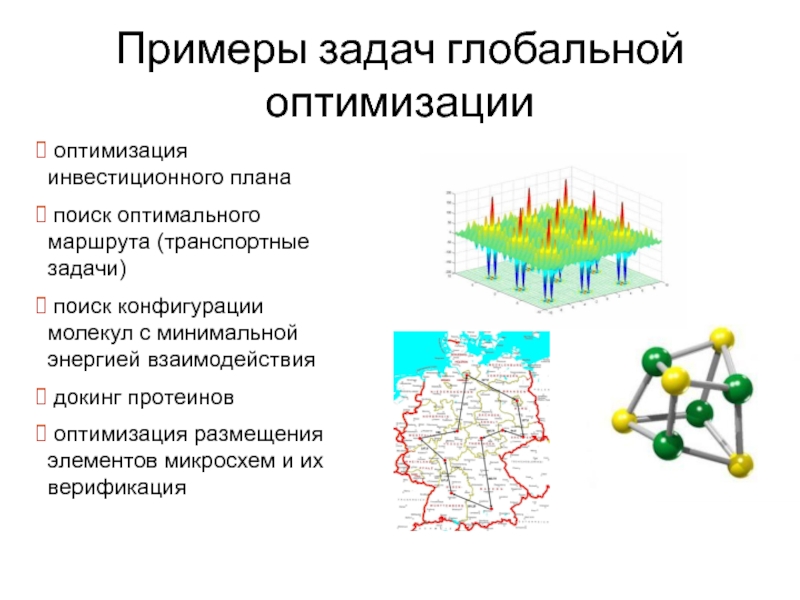
Слайд 8Примеры задач глобальной оптимизации
оптимизация инвестиционного плана
поиск оптимального маршрута (транспортные
поиск конфигурации молекул с минимальной энергией взаимодействия
докинг протеинов
оптимизация размещения элементов микросхем и их верификация
Слайд 9Метод Неравномерных Покрытий
Предложен Ю.Г. Евтушенко в 1971 году
Позволяет решать
задачи без
с нелинейными ограничениями,
частично-целочисленные задачи
с одним и несколькими критериями
Гарантирует оптимальность с заданной точностью (детерминированный метод)
Слайд 10Метод неравномерных покрытий
Предложен для безусловной оптимизации в 1971
Ю. Г. Евтушенко, “Численный
Расширен на случай многих критериев в 1986 Евтушенко Ю. Г., Потапов М. А. «Методы численного решения многокритериальных задач.» ДАН СССР, Т. 291, N 1, 1986, С. 25-39.
Расширен на задачи математического программирования в 1992 Yu. G. Evtushenko, M. A. Potapov, V. V. Korotkikh. Numerical methods for global optimization. In "Recent advances in global optimization”, Princeton University Press, pp. 274-297. 1992.
Первая параллельная реализация 2007 Ю. Г. Евтушенко, В. У. Малкова, А. А. Станевичюс. Распараллеливание процесса поиска глобального экстремума. Автоматика и телемеханика, № 5. С. 46-58, 2007.
Новая техника для задач математического программирования 2011 Ю. Г. Евтушенко, М. А. Посыпкин. Варианты метода неравномерных покрытий для глобальной оптимизации частично-целочисленных нелинейных задач. Доклады Академии наук. Т: 437. № 2. С. 168–172.
Слайд 12Упрощение постановки
От безусловной переходим к оптимизации с простыми (параллелепипедными) ограничениями («box-constrained»)
Требуется
Слайд 13Метод неравномерных покрытий для одномерной безусловной оптимизации
[
a
]
b
]
a’
[
b’
Миноранта
Лебеговское множество
Целевая функция
Слайд 15Общий случай: основная теорема
L2
L3
L4
L5
L6
- совокупность множеств
Теорема. Если выполнено
- совокупность допустимых точек
Слайд 16Основные составляющие МНП
Построение покрытия (системы покрывающих множеств)
Построение последовательности рекордных точек
Слайд 17Липшицева Миноранта 1-го порядка
Условие Липшица:
Миноранта:
представляет собой шар радиуса
с центром в
Слайд 18Липшицева миноранта 2-го порядка
Градиент удовлетворяет условию Липшица
Миноранта
- шар радиуса
с центром
Этот шар может быть исключен из дальнейшего рассмотрения.
Слайд 28Нахождение хорошего рекорда
Использование локальных и эвристических методов позволяет найти хороший рекорд
Слайд 32Оптимизация с ограничениями: основная идея
Если -
то множество
можно отбросить как не содержащее допустимых точек.
Слайд 33Оптимизация с ограничениями: основная теорема
L2
L3
L4
L5
L6
- совокупность множеств
Теорема. Если выполнено
- совокупность -допустимых точек
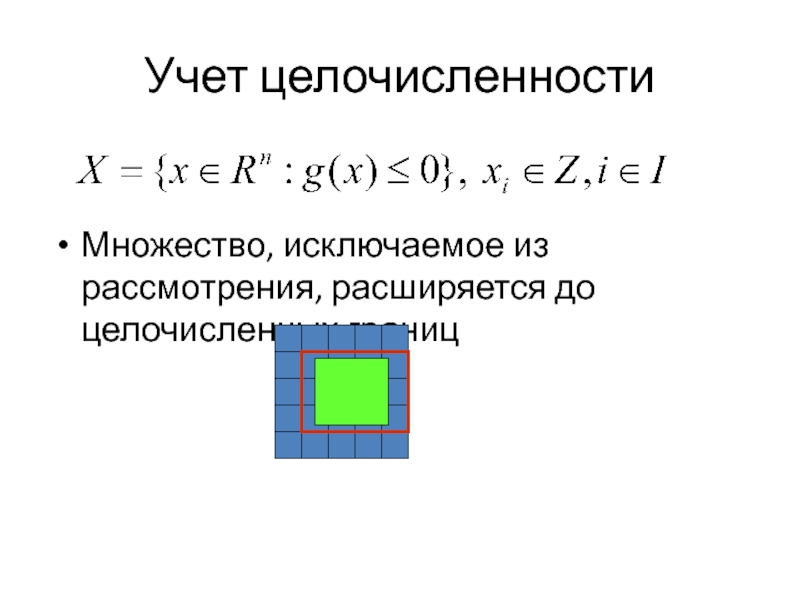
Слайд 34Учет целочисленности
Множество, исключаемое из рассмотрения, расширяется до целочисленных границ
Слайд 35Частично целочисленные задачи
Требуется минимизировать затраты f(x) на производство при соблюдении технологических
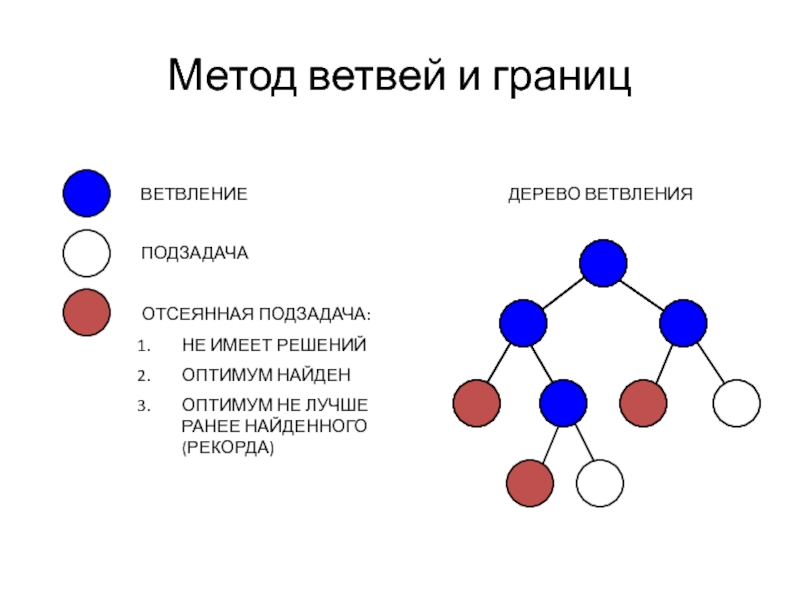
Слайд 37Метод ветвей и границ
ДЕРЕВО ВЕТВЛЕНИЯ
ВЕТВЛЕНИЕ
ПОДЗАДАЧА
ОТСЕЯННАЯ ПОДЗАДАЧА:
НЕ ИМЕЕТ РЕШЕНИЙ
ОПТИМУМ НАЙДЕН
ОПТИМУМ НЕ ЛУЧШЕ
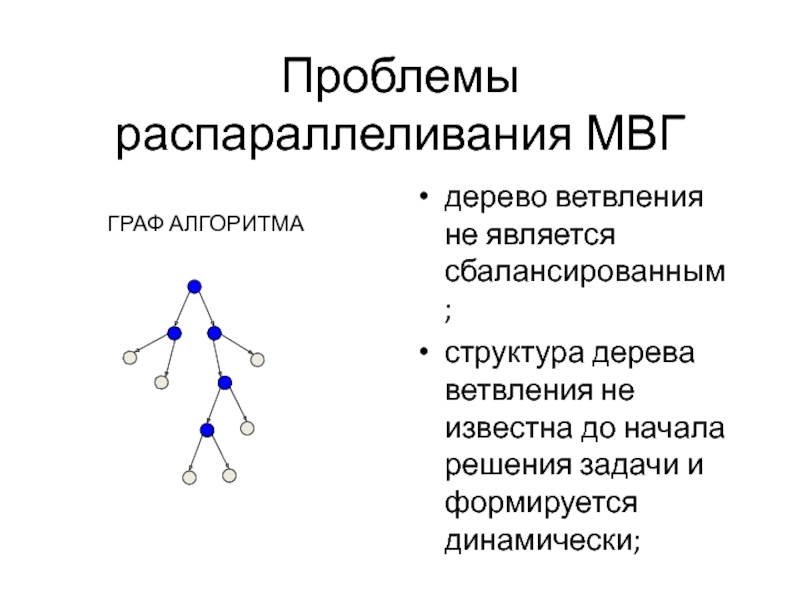
Слайд 38Проблемы распараллеливания МВГ
дерево ветвления не является сбалансированным;
структура дерева ветвления не известна
ГРАФ АЛГОРИТМА
Слайд 40
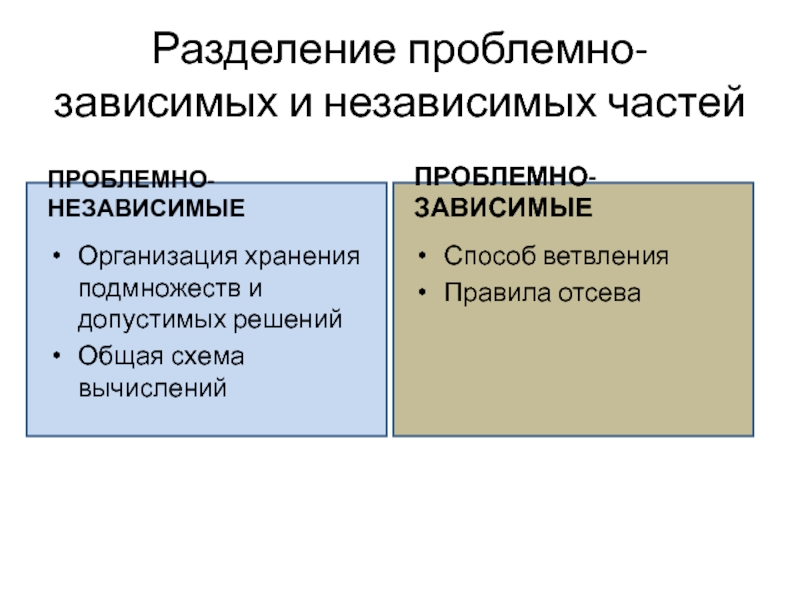
Разделение проблемно-зависимых и независимых частей
ПРОБЛЕМНО-НЕЗАВИСИМЫЕ
Организация хранения подмножеств и допустимых решений
Общая схема
ПРОБЛЕМНО-ЗАВИСИМЫЕ
Способ ветвления
Правила отсева
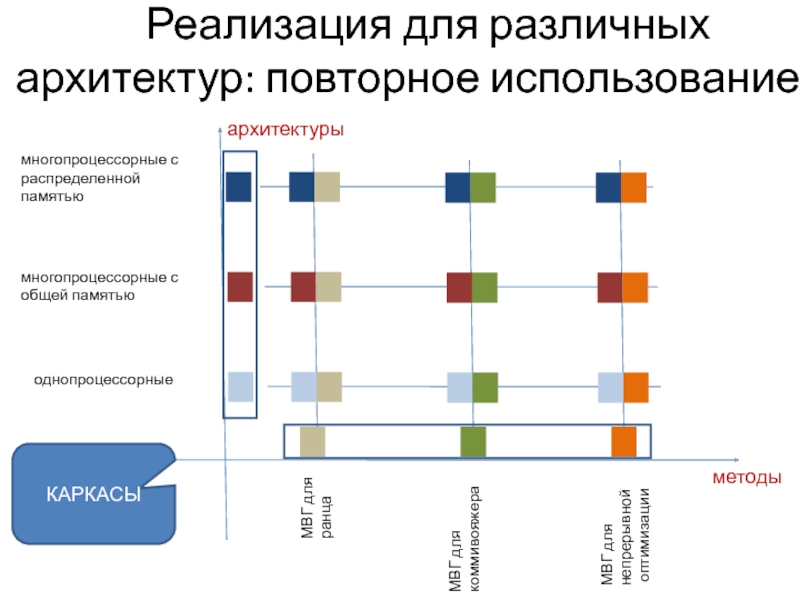
Слайд 41 Реализация для различных архитектур: повторное использование
многопроцессорные с распределенной памятью
однопроцессорные
многопроцессорные с общей
архитектуры
методы
МВГ для
ранца
МВГ для
коммивояжера
МВГ для
непрерывной
оптимизации
КАРКАСЫ
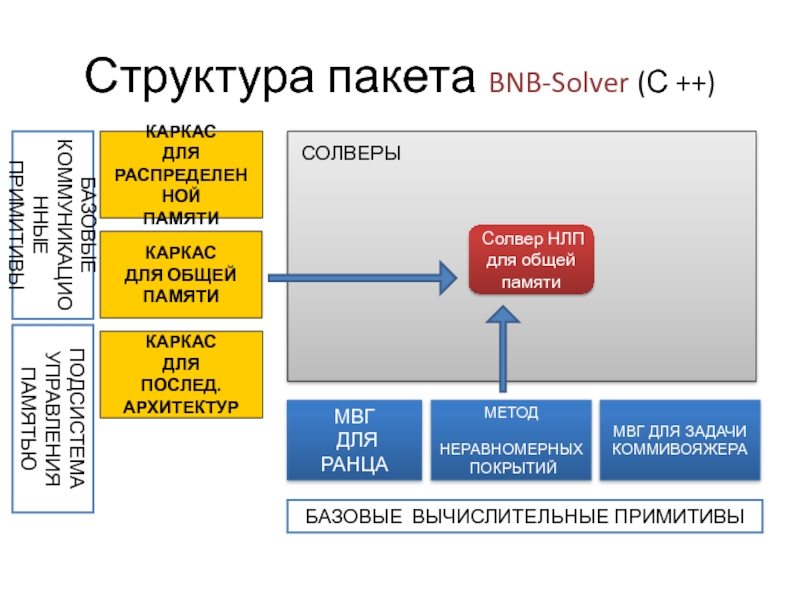
Слайд 42Структура пакета BNB-Solver (С ++)
БАЗОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ ПРИМИТИВЫ
БАЗОВЫЕ КОММУНИКАЦИОННЫЕ ПРИМИТИВЫ
КАРКАС
ДЛЯ ОБЩЕЙ
КАРКАС
ДЛЯ
РАСПРЕДЕЛЕННОЙ
ПАМЯТИ
МЕТОД
НЕРАВНОМЕРНЫХ
ПОКРЫТИЙ
МВГ
ДЛЯ РАНЦА
КАРКАС
ДЛЯ
ПОСЛЕД.
АРХИТЕКТУР
МВГ ДЛЯ ЗАДАЧИ
КОММИВОЯЖЕРА
Солвер НЛП для общей памяти
СОЛВЕРЫ
ПОДСИСТЕМА УПРАВЛЕНИЯ ПАМЯТЬЮ
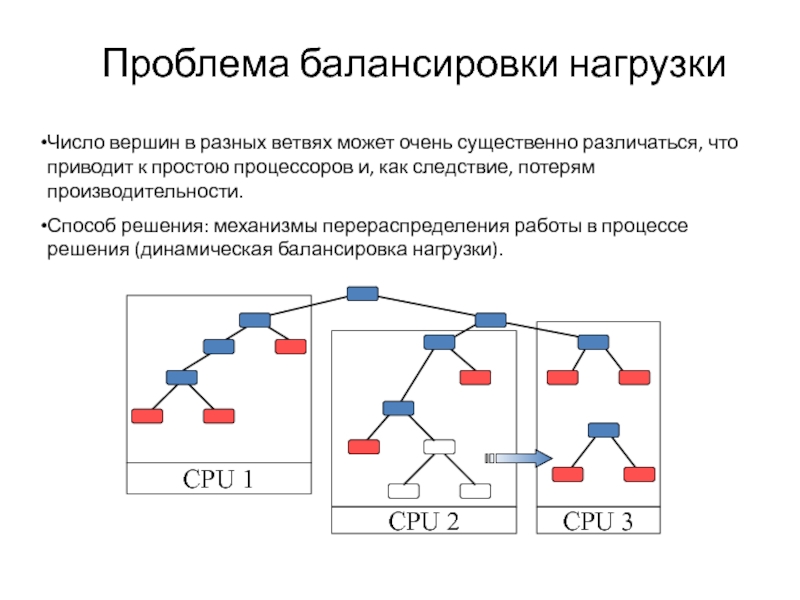
Слайд 43Проблема балансировки нагрузки
Число вершин в разных ветвях может очень существенно различаться,
Способ решения: механизмы перераспределения работы в процессе решения (динамическая балансировка нагрузки).
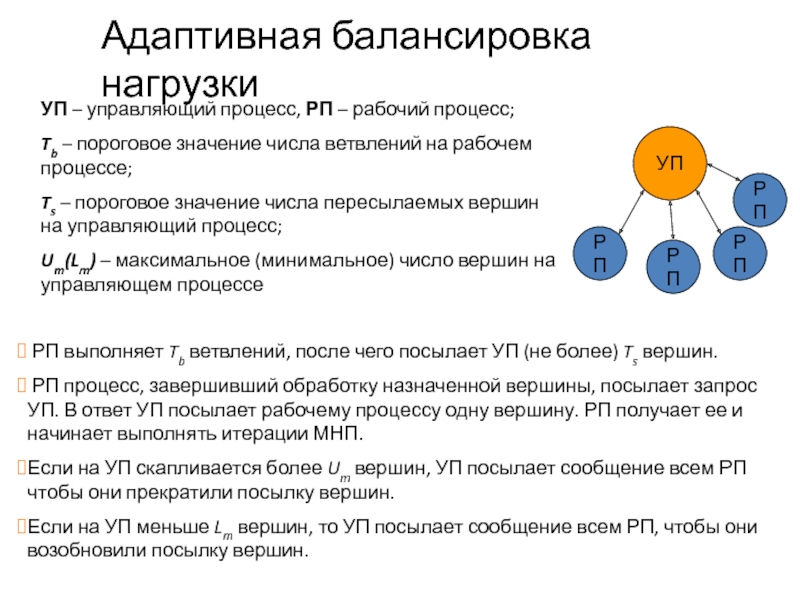
Слайд 44Адаптивная балансировка нагрузки
РП выполняет Tb ветвлений, после чего посылает УП
РП процесс, завершивший обработку назначенной вершины, посылает запрос УП. В ответ УП посылает рабочему процессу одну вершину. РП получает ее и начинает выполнять итерации МНП.
Если на УП скапливается более Um вершин, УП посылает сообщение всем РП чтобы они прекратили посылку вершин.
Если на УП меньше Lm вершин, то УП посылает сообщение всем РП, чтобы они возобновили посылку вершин.
УП
РП
РП
РП
РП
УП – управляющий процесс, РП – рабочий процесс;
Tb – пороговое значение числа ветвлений на рабочем процессе;
Ts – пороговое значение числа пересылаемых вершин на управляющий процесс;
Um(Lm) – максимальное (минимальное) число вершин на управляющем процессе
Слайд 46Современные проблемы МНП
Усовершенствование метода
Новые способы построения покрытий
Ускорение получения рекордов
Решение многокритериальных задач
Слайд 47Проблемы эффективной реализации
Преодоление 100 TFLOPS: совершенствование балансировки
Перенос на гибридные архитектуры (распределенная
Реализация в распределенной среде (BOINC-проекты: OPTIMA@home)










![Метод неравномерных покрытий для одномерной безусловной оптимизации[a]b]a’[b’МинорантаЛебеговское множествоЦелевая функция](/img/tmb/2/165310/424ae7f1ea829b3b08d772bc46cce49e-800x.jpg)
![Метод неравномерных покрытий для одномерной безусловной оптимизации[a]b](/img/tmb/2/165310/cc9e2efa8cd6a992068f0182f3333f21-800x.jpg)