- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первый признак подобия треугольников. Урок 1. презентация
Содержание
Слайд 1
*
Первый признак подобия треугольников.
Урок 1.
ГОУ СОШ №1280 ЮЗАО г. Москвы
Замковая Татьяна
Слайд 23. Два треугольника подобны. Два угла одного треугольника 1200 и 500.
Ответ: 100
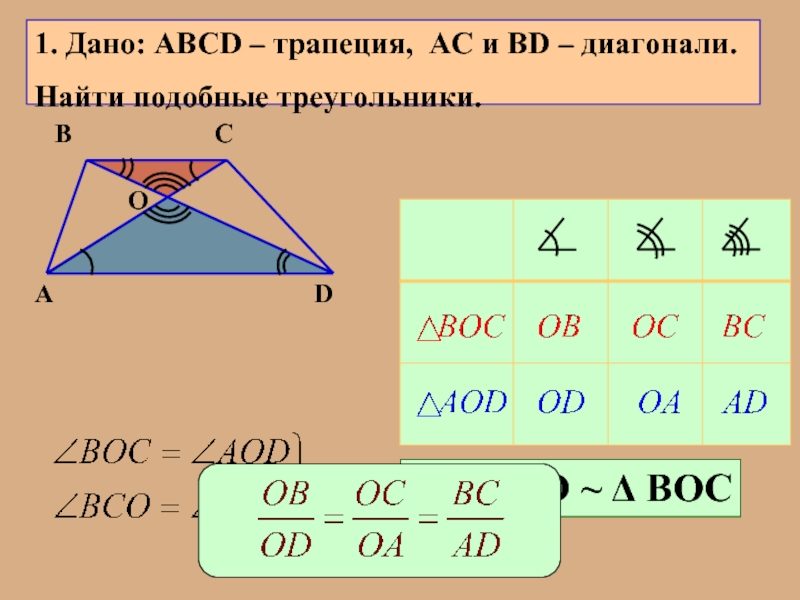
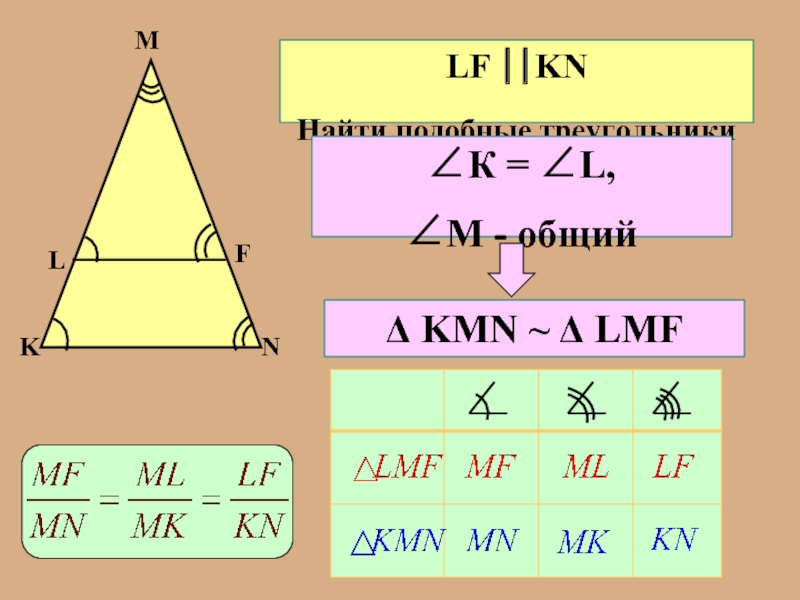
1. Какие треугольники называются подобными?
2. Сформулировать теорему об отношении площадей треугольников, имеющих по равному углу.
4. У подобных треугольников сходственные стороны равны 3 см и 9 см. Площадь первого треугольника равна 8 см2. Найдите площадь второго треугольника.
Ответ: 72 см2
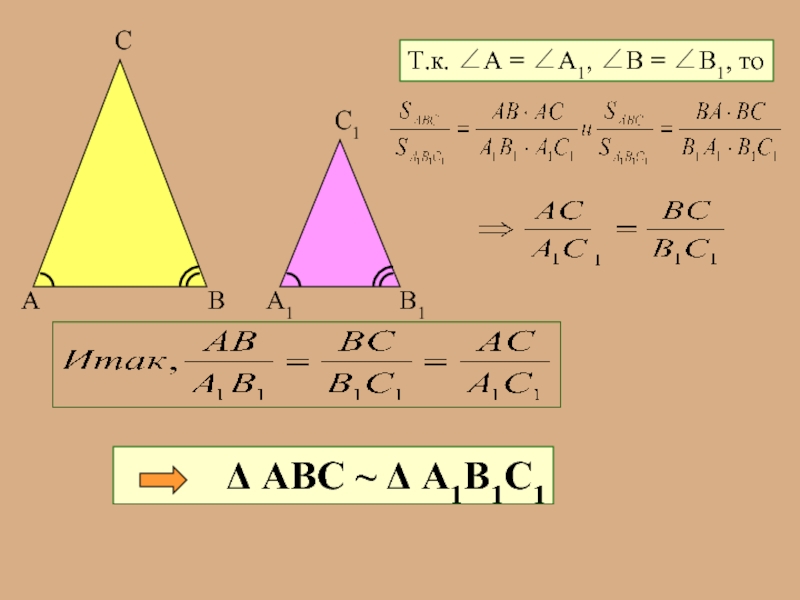
Слайд 3Теорема 1. Если два угла одного треугольника соответственно равны двум углам
А
В
С
А1
В1
С1
Доказать: Δ АВС ~ Δ А1В1С1
Доказательство:
Т.к. ∠А = ∠А1, ∠С = ∠С1, то:
Итак, ∠А=∠А1, ∠В=∠В1, ∠С=∠С1.
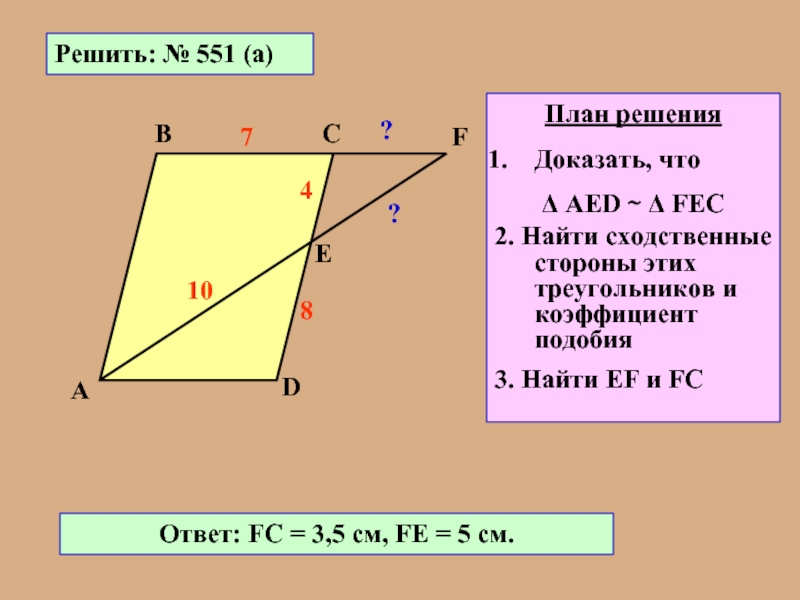
Слайд 7Решить: № 551 (а)
А
В
С
D
Е
F
8
4
7
10
?
?
План решения
Доказать, что
Δ АЕD ∼ Δ FЕС
2.
3. Найти ЕF и FC
Ответ: FC = 3,5 см, FЕ = 5 см.
Слайд 8Список используемой литературы:
1) Геометрия, 7-9: Учеб. Для общеобразоват. учреждений/ Л.С.
М.: Просвещение, АО «Московские учебники», 2001.