- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Касательная к окружности. Решение задач. презентация
Содержание
- 1. Касательная к окружности. Решение задач.
- 2. Теоретический тест. Среди
- 3. Теоретический тест. Окружность
- 4. Теоретический тест. Истинно
- 5. Теоретический тест. Сформулируйте:
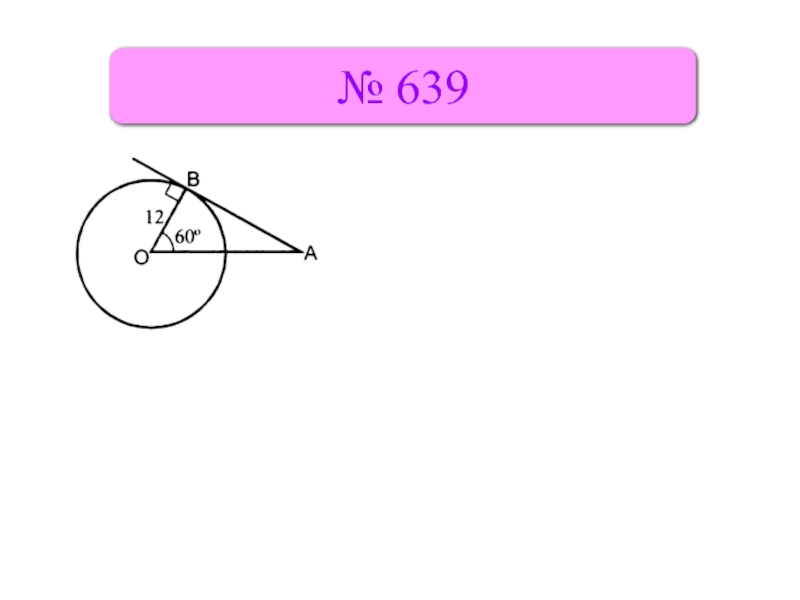
- 6. № 639
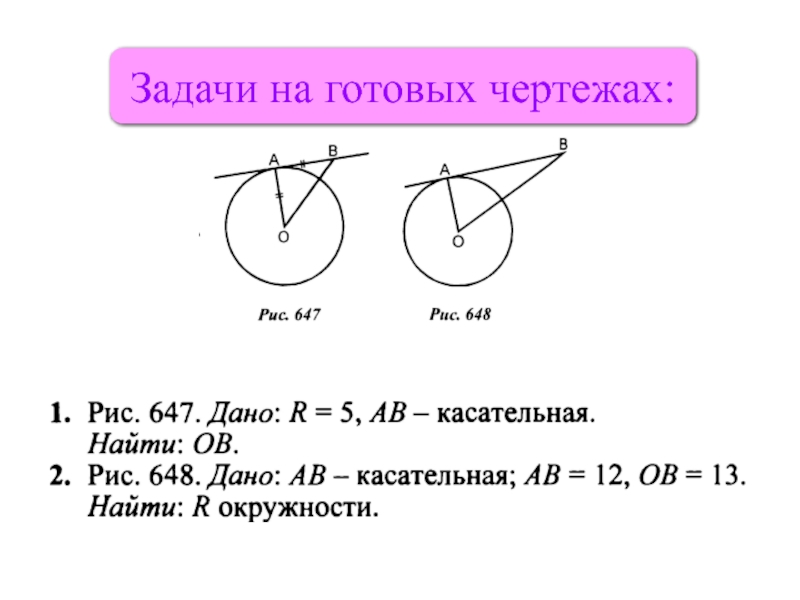
- 7. Задачи на готовых чертежах:
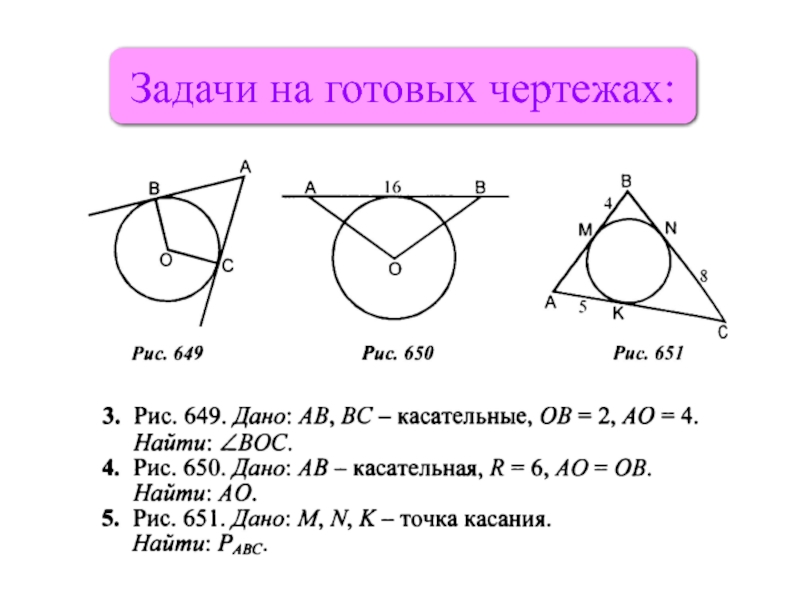
- 8. Задачи на готовых чертежах:
- 9. Рабочая тетрадь - №84
- 10. Самостоятельная работа:
- 11. Домашнее задание: №№ 641, 643, 645, 648
Теоретический тест. Среди следующих утверждений укажите истинные. Окружность и прямая имеют две общих точки, если: расстояние от центра окружности до прямой не превосходит радиуса окружности; расстояние от
Слайд 2Теоретический тест.
Среди следующих утверждений укажите истинные.
Окружность и прямая имеют две общих
точки, если:
расстояние от центра окружности до прямой не превосходит радиуса окружности;
расстояние от центра окружности до прямой меньше радиуса окружности;
расстояние от окружности до прямой меньше радиуса окружности;
расстояние от центра окружности до прямой не превосходит радиуса окружности;
расстояние от центра окружности до прямой меньше радиуса окружности;
расстояние от окружности до прямой меньше радиуса окружности;
1
Слайд 4Теоретический тест.
Истинно или ложно?
Прямая является секущей по отношению к окружности, если
она имеет
с окружностью общие точки.
Прямая является секущей по отношению к окружности, если она пересекает
окружность в двух точках.
Прямая является секущей по отношению к окружности, если расстояние
от центра окружности до данной прямой не больше радиуса.
с окружностью общие точки.
Прямая является секущей по отношению к окружности, если она пересекает
окружность в двух точках.
Прямая является секущей по отношению к окружности, если расстояние
от центра окружности до данной прямой не больше радиуса.
3
Слайд 5Теоретический тест.
Сформулируйте:
теорему о свойстве касательной.
теорему о свойстве отрезков касательных к окружности,
проведенных из одной точки.
теорему, обратную теореме о свойстве касательной.
теорему, обратную теореме о свойстве касательной.
4
