- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к решению задач презентация
Содержание
- 1. Применение производной к решению задач
- 2. Цели занятия Уточнить основные понятия и законы
- 3. Задание 1 1. Зная правило дифференцирования произведения
- 4. Задание 2 Составить алгоритм отыскания промежутков выпуклости
- 5. Задание 3 Установить соответствие между
- 6. Работа первой группы № 1.
- 7. Работа первой группы № 2. D(у)=R, , у΄>0 при х
- 8. Работа второй группы Напишите уравнение касательной к графику функции у=-х³-6х²+3, которая имеет наибольший угловой коэффициент.
- 9. Работа третьей группы № 1.
- 11. Работа третьей группы 1. V(t)=x΄(t), V(t)=36t –
- 12. Домашнее задание
Слайд 2Цели занятия
Уточнить основные понятия и законы темы, углублённо рассмотреть конкретные вопросы
Провести самостоятельное исследование по теме, перенос знаний в нестандартную ситуацию.
Проявить и развить свои способности, организовать свои цели, составить реальный план, выполнить его и оценить свои результаты.
Слайд 3Задание 1
1. Зная правило дифференцирования произведения двух функций, составьте формулу (u∙v∙w)΄
2. Зная связь первой производной и
экстремумов, установите, как определить вид экстремума по второй производной.
(u∙v∙w)΄ = u΄∙v∙w + u∙v΄∙w + u∙v∙w΄
Слайд 4Задание 2
Составить алгоритм отыскания промежутков выпуклости вверх и вниз
1. у΄=12х5 – 20х³
2. у΄΄=60(х²)² – 60х²
3. у΄΄=0 при х=0, х=1, х=-1.
4. у΄΄> 0, функция выпукла вниз при
х ≤ -1, х ≥ 1.
5. у΄΄< 0, функция выпукла вверх при
-1 ≤ х ≤ 1.
Слайд 5Задание 3
Установить соответствие между предложенными графиками у=f΄(x) и формулами,
1. у= х²-1 2. у=х³- 1 3. у=(х-1)² 4. у=-х² -1
А Б В Г
Ответы: 1- Б, 2 – А, 3 – Г, 4 – В.
Слайд 6Работа первой группы
№ 1.
Для графика функции у=f(x): f΄(x)>0 и f(x) возрастает [-5;-2,8],[-0,4;3,5]
f΄(x)<0 и f(x) убывает [-2,8;-0,4,[3,5;5]
f΄(x)=0 и производная меняет знак с плюса на
минус при х=-2,8 и х=3,5 и х=-2,8 и х=3,5
точки максимума
f΄(x)=0 и производная меняет знак с минуса на
плюс при х=-0,4 и х=-0,4 точка минимума
Для графика функции у=f ΄΄(х): f΄(x) убывает на промежутках [-3,5;-1,5],
[0,5;1,5], [2,8;5] значит функция у=f΄΄(x)
отрицательна на этих промежутках и
обращается в нуль при х=-3,5, х=-1,5,х=0,5,
х=1,5, х=2,8
f΄(x) возрастает на промежутках [-5;-3,5],
[-1,5;0,5], [1,5;2,8] значит функция у=f΄΄(x)
положительна на этих промежутках.
Слайд 7Работа первой группы
№ 2.
D(у)=R, , у΄>0 при х
Слайд 8Работа второй группы
Напишите уравнение касательной к графику функции у=-х³-6х²+3, которая имеет
Слайд 9Работа третьей группы
№ 1.
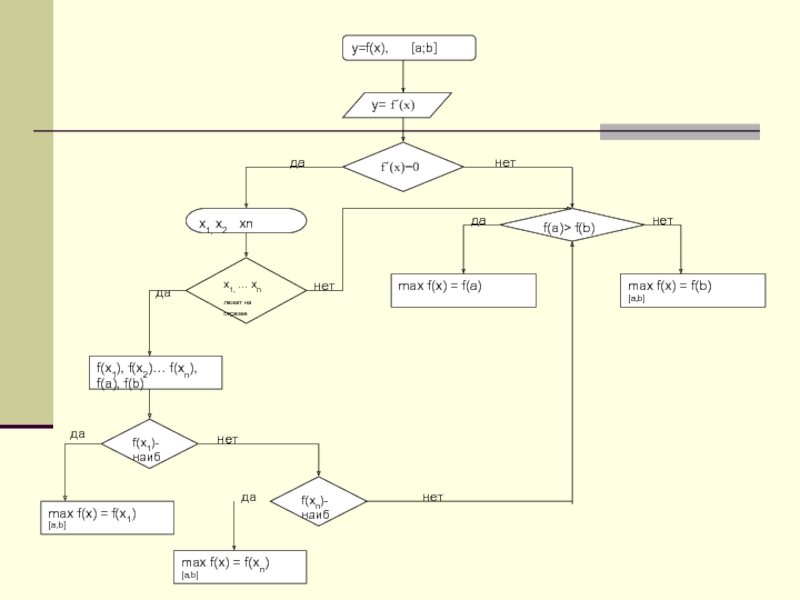
Найти наибольшее значение функции y=f(x)
1. Найти производную данной функции.
2. Найти критические точки.
3. Выбрать критические точки, принадлежащие заданному отрезку.
4. Найти значение функции в отобранных критических точках и концах отрезка.
5. Выбрать наибольшее значение функции.
Слайд 11Работа третьей группы
1. V(t)=x΄(t), V(t)=36t – 3t2
2. V΄ (t)= 36 –
3. V΄ (t)=0 при t=6
4. 6 принадлежит отрезку [4,8]
5. V(4)=96 м/с, V(6)=108 м/с,
V(8)=96м/с
6. max V(t) = V(6) =108 м/с








![Работа третьей группы№ 1. Найти наибольшее значение функции y=f(x) на отрезке [a,b].1. Найти производную](/img/tmb/1/27122/e581c7bcb727a8d97b7d795a5d6f052d-800x.jpg)