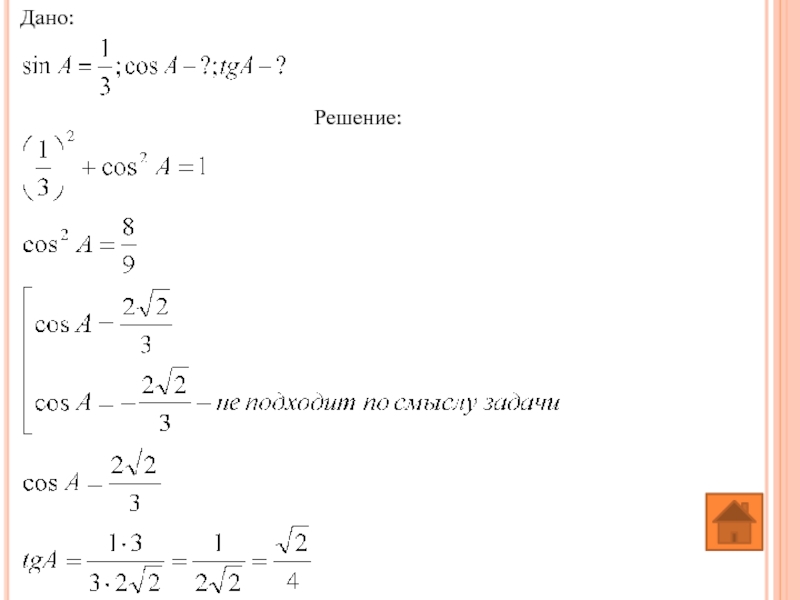488(учитель Курышова Н.Е).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрия глава 7 Подобные треугольники. презентация
Содержание
- 1. Геометрия глава 7 Подобные треугольники.
- 2. Оглавление 1.Определение подобных треугольников а)пропорциональные отрезки б)определение
- 3. Подобные треугольники
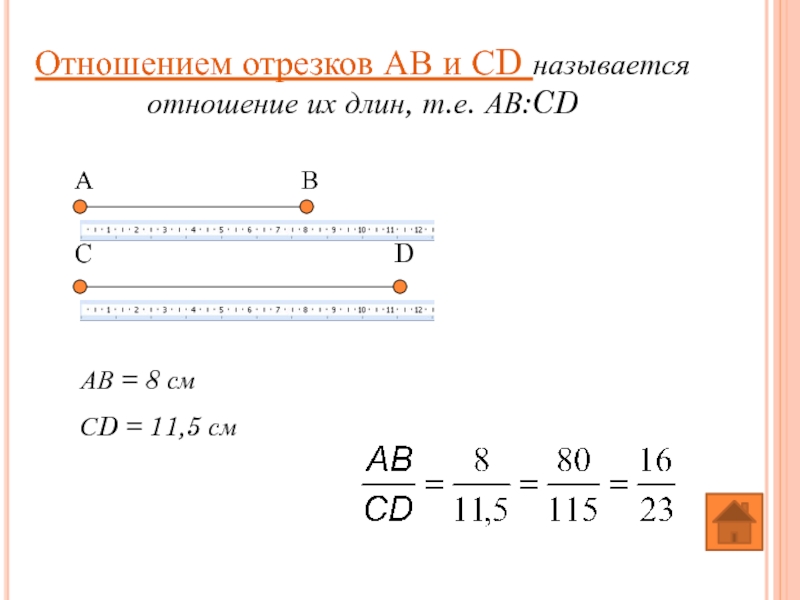
- 4. Отношением отрезков АВ и СD называется отношение
- 5. Отрезки АВ и CD пропорциональны отрезкам А1В1
- 6. Подобные фигуры- это фигуры одинаковой формы
- 7. Если в треугольниках все углы соответственно равны,
- 8. Два треугольника называются подобными, если их углы
- 9. Задача
- 10. назад Стороны
- 11. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия Доказательство:
- 12. Признаки подобия треугольников
- 13. Первый признак подобия треугольников Если два угла
- 14. Доказательство
- 15. Задача
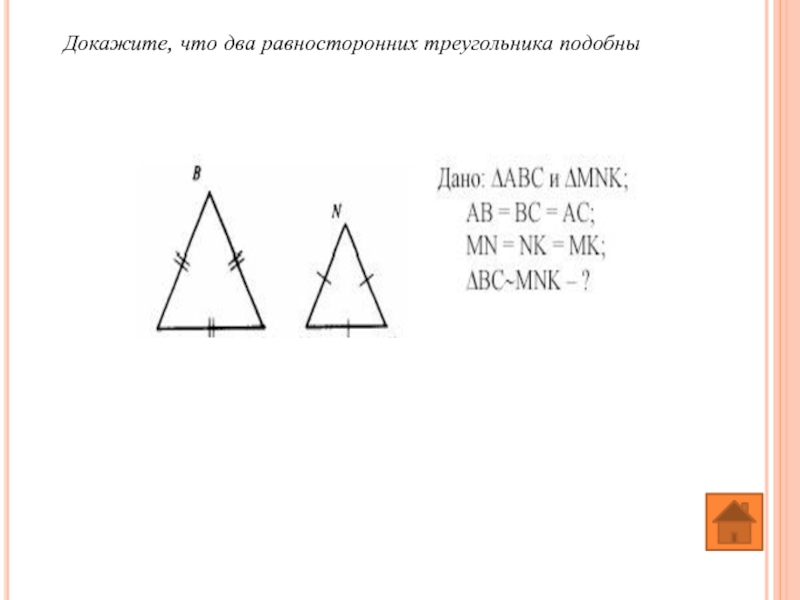
- 16. Докажите, что два равносторонних треугольника подобны
- 17. Второй признак подобия треугольников Если две стороны
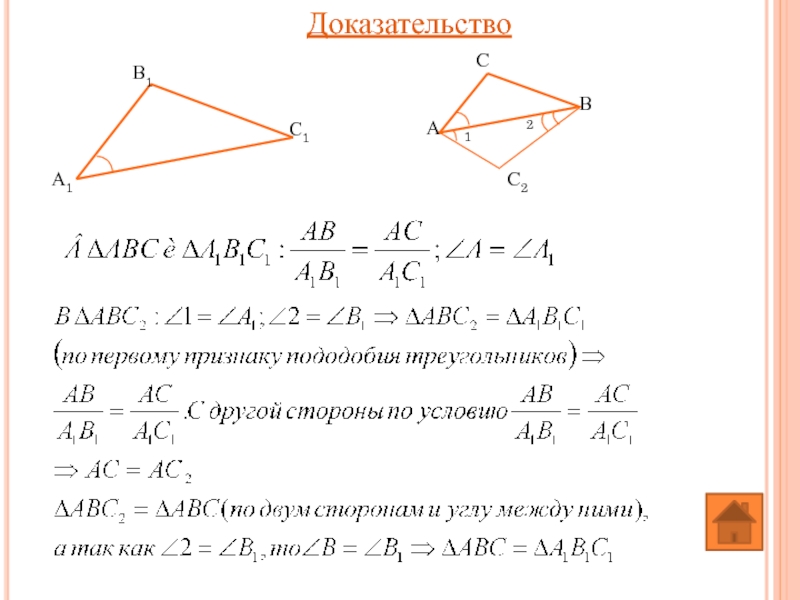
- 18. Доказательство
- 19. Задача
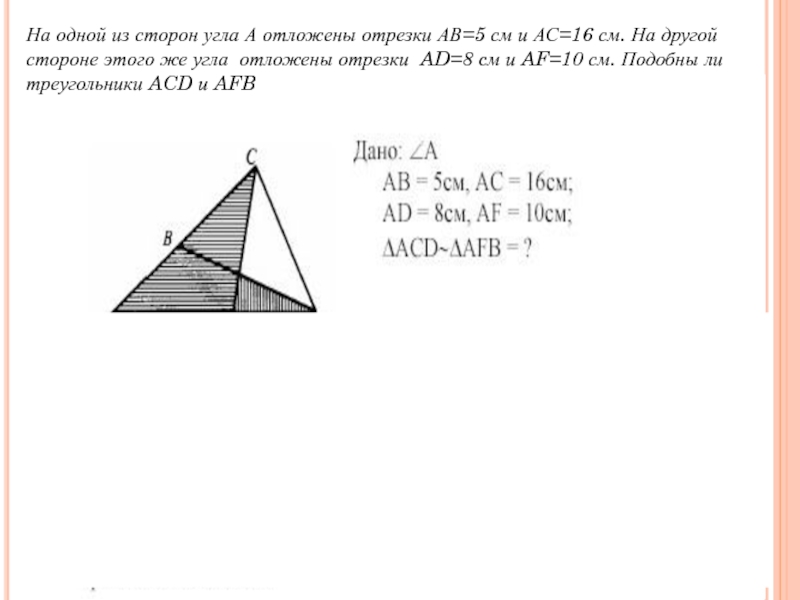
- 20. На одной из сторон угла А отложены
- 21. Третий признак подобия треугольников Если три стороны
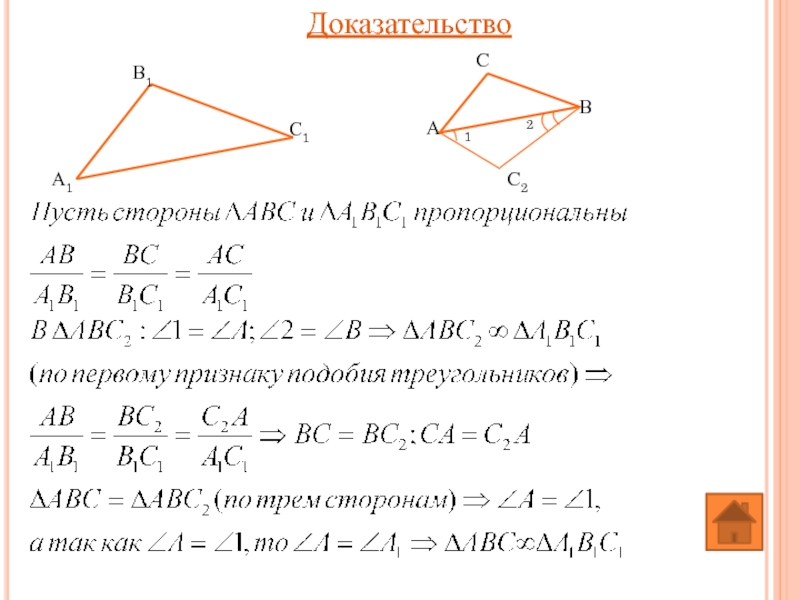
- 22. Доказательство
- 23. Применение подобия к доказательству теорем и решению задач
- 24. Средней линией называется отрезок, соединяющий середины двух
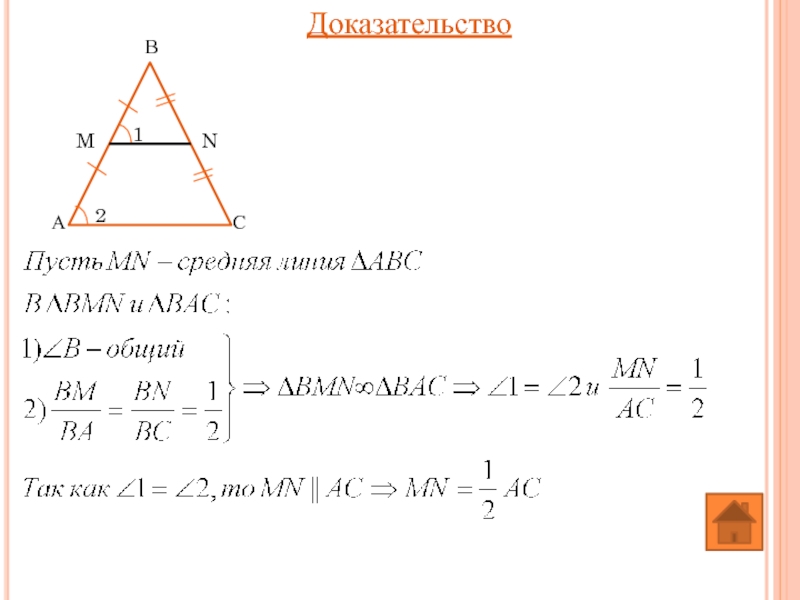
- 25. Доказательство
- 26. Задача
- 27. Точки P и Q-середины
- 28. Теорема: Медианы треугольника пересекаются в одной точке,
- 29. Доказательство
- 30. Задача
- 31. В треугольнике АВС медианы АА1 и
- 32. Теорема: Высота прямоугольного треугольника, проведенная из вершины
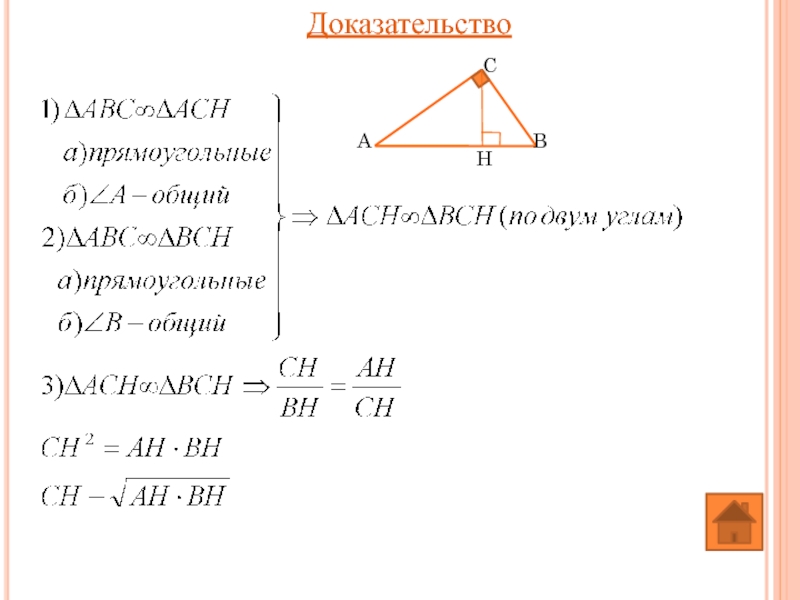
- 33. Теорема: Высота прямоугольного треугольника, проведённая из вершины
- 34. Доказательство
- 35. Определение высоты предмета: Определить высоту телеграфного столба Практические приложения подобия треугольников
- 36. Задача
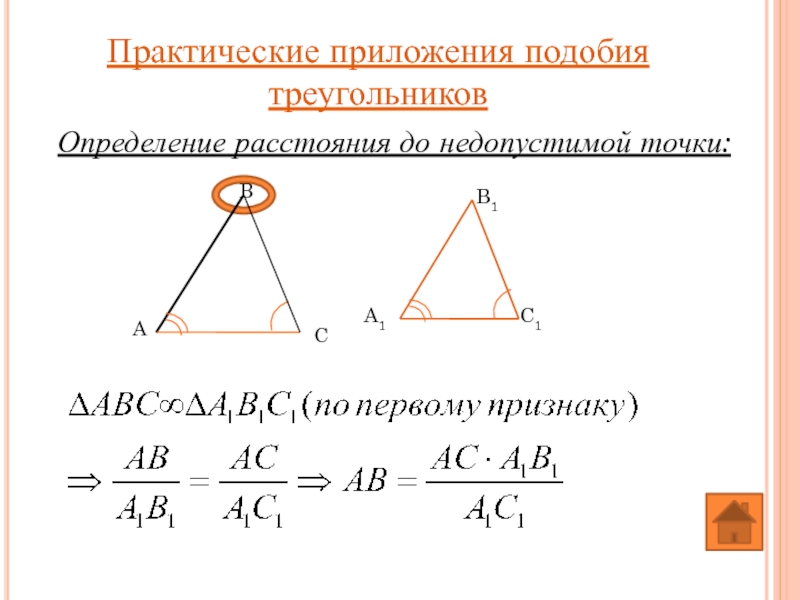
- 38. Определение расстояния до недопустимой точки: Практические приложения подобия треугольников
- 39. Задача
- 40. Для определения расстояния от точки
- 41. Соотношение между сторонами и углами прямоугольного треугольника
- 42. Синус, косинус и тангенс острого угла прямоугольного
- 43. Синус, косинус и тангенс острого угла прямоугольного треугольника
- 44. Значение синуса, косинуса и тангенса для углов 300, 450, 600
- 45. Задача
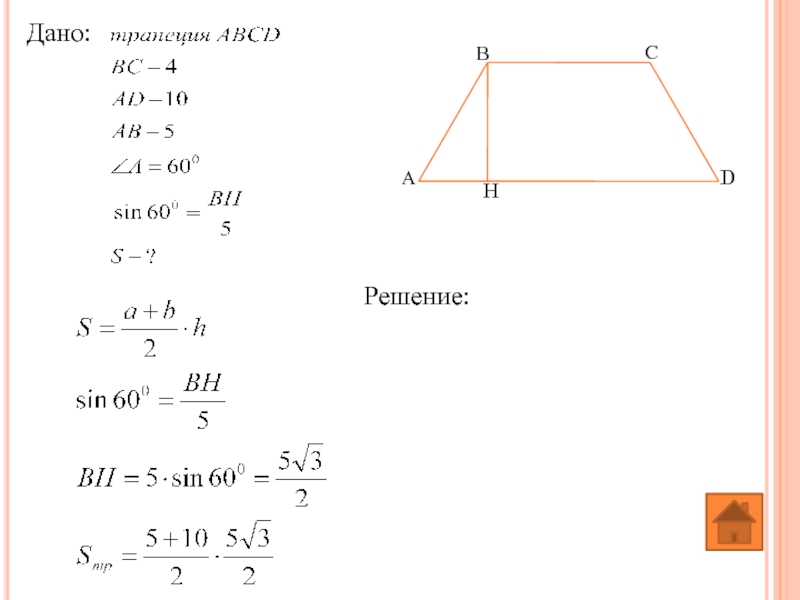
- 46. Дано: Решение:
- 47. Значение синуса, косинуса и тангенса для углов 300, 450, 600
- 48. Задача
- 49. Дано: Решение:
- 50. Конец
Оглавление 1.Определение подобных треугольников а)пропорциональные отрезки б)определение подобных треугольников в)Отношение площадей 2.Признаки подобия треугольников а)Первый признак подобия б)Второй признак подобия в)Третий признак подобия 3.Применение подобия к доказательству теорем и решению
Слайд 1Геометрия
глава 7
Подобные треугольники.
Подготовила Пономарева Кристина ученица 9 класса СПб лицей
Слайд 2Оглавление
1.Определение подобных треугольников
а)пропорциональные отрезки
б)определение подобных треугольников
в)Отношение площадей
2.Признаки подобия треугольников
а)Первый признак подобия
б)Второй
признак подобия
в)Третий признак подобия
в)Третий признак подобия
3.Применение подобия к доказательству теорем и решению задач
а)Средняя линия треугольника
б)Пропорциональные отрезки в прямоугольном треугольнике
в)Практические приложения подобия треугольников
4.Соотношение между сторонами и углами прямоугольного треугольника
а)Синус, косинус и тангенс острого угла прямоугольного треугольника
б)Значение синуса, косинуса и тангенса для углов 300, 450 и 600
Слайд 5Отрезки АВ и CD пропорциональны отрезкам А1В1 и С1D1, если:
С1D1= 6
см
АВ= 4 см
CD= 8 см
А1В1=3 см
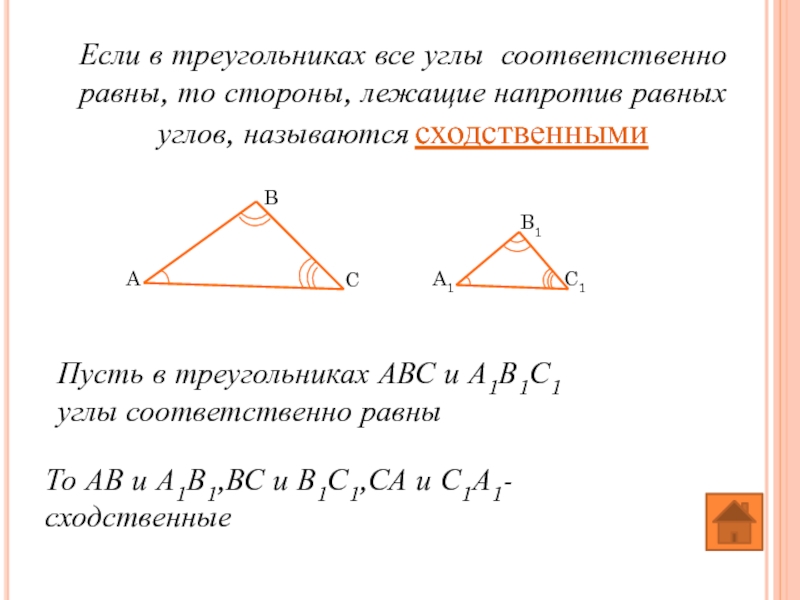
Слайд 7Если в треугольниках все углы соответственно равны, то стороны, лежащие напротив
равных углов, называются сходственными
Пусть в треугольниках АВС и А1В1С1 углы соответственно равны
То АВ и А1В1,ВС и В1С1,СА и С1А1-сходственные
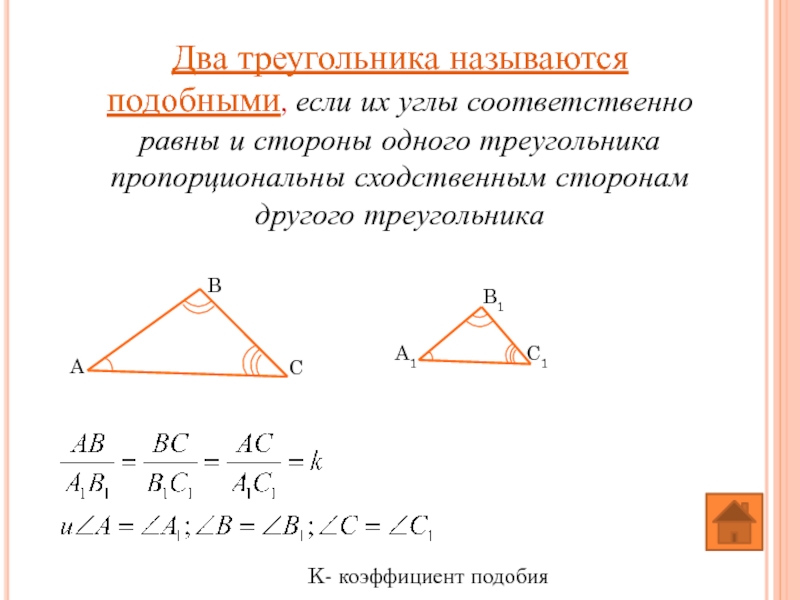
Слайд 8Два треугольника называются подобными, если их углы соответственно равны и стороны
одного треугольника пропорциональны сходственным сторонам другого треугольника
K- коэффициент подобия
Слайд 10назад
Стороны одного треугольника равны 15 см, 20 см, и
30 см. Найдите стороны треугольника, подобного данному, если периметр равен 26 см
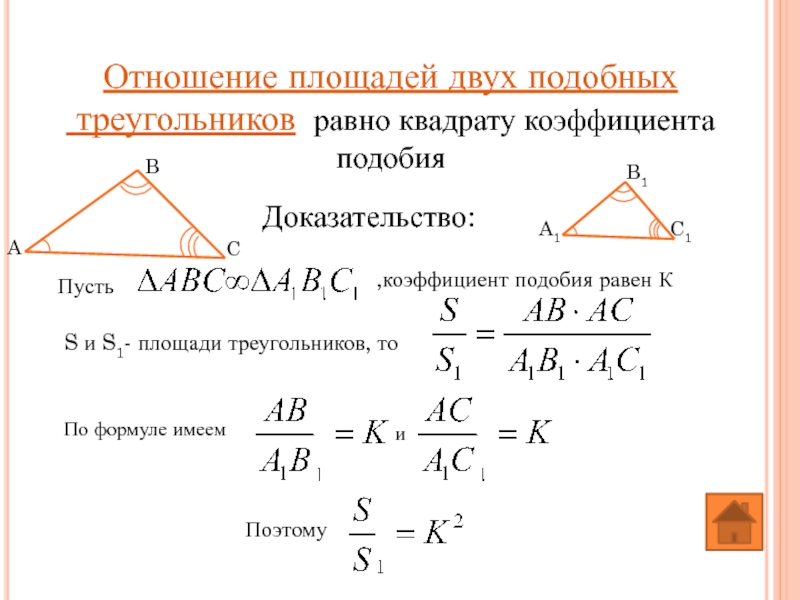
Слайд 11Отношение площадей двух подобных
треугольников равно квадрату коэффициента подобия
Доказательство:
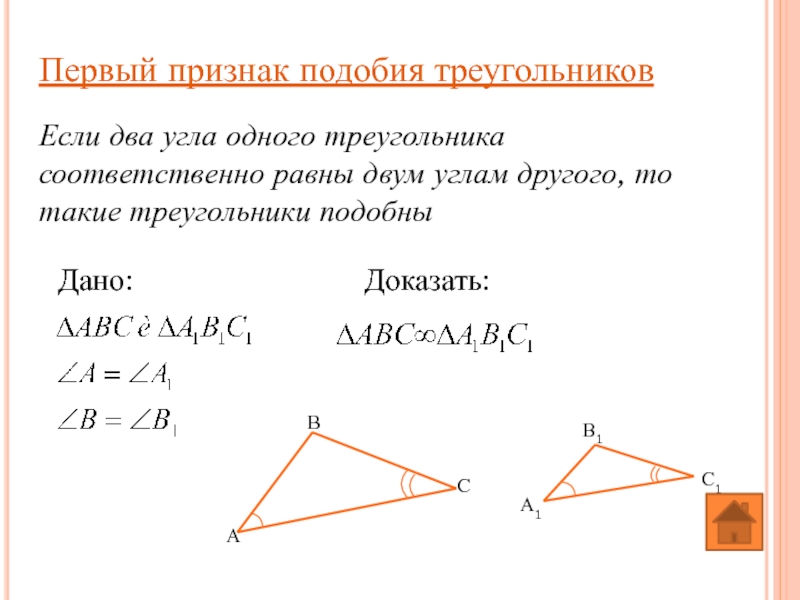
Слайд 13Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум
углам другого, то такие треугольники подобны
Дано:
Доказать:
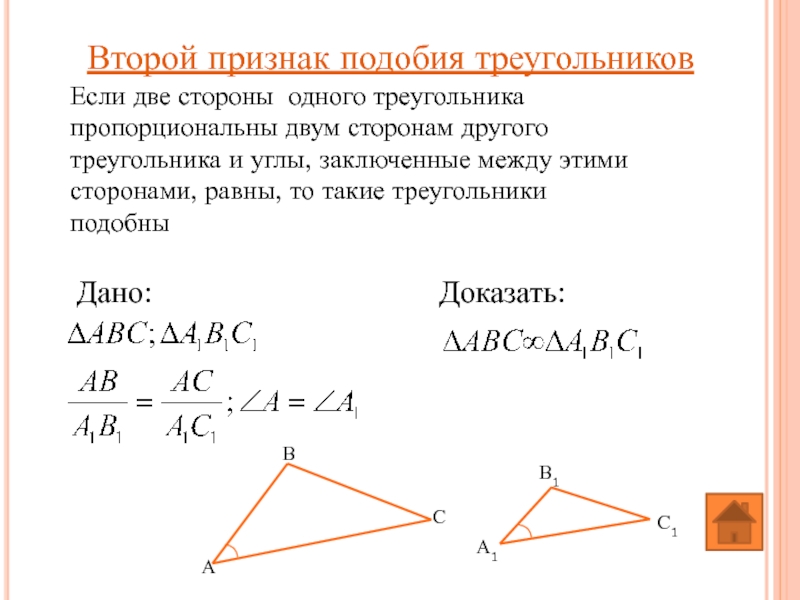
Слайд 17Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам
другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Дано:
Доказать:
Слайд 20На одной из сторон угла А отложены отрезки АВ=5 см и
АС=16 см. На другой стороне этого же угла отложены отрезки AD=8 cм и AF=10 см. Подобны ли треугольники ACD и AFB
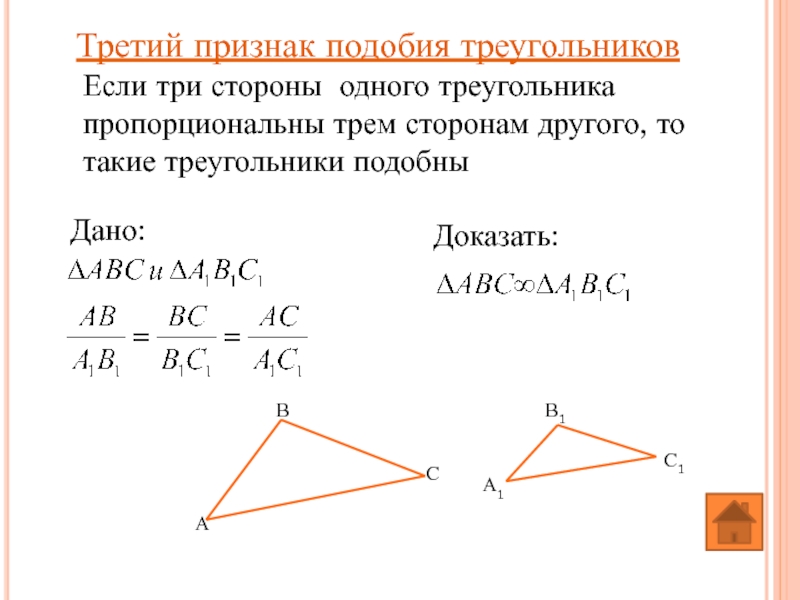
Слайд 21Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам
другого, то такие треугольники подобны
Дано:
Доказать:
Слайд 24Средней линией называется отрезок, соединяющий середины двух его сторон
Теорема:
Средняя линия
треугольника параллельна одной из его сторон и равна половине этой стороны
Дано:
Доказать:
Слайд 27
Точки P и Q-середины сторон АВ и АС треугольника АВС. Найдите
периметр треугольника АВС, если периметр треугольника APQ равен 21 см
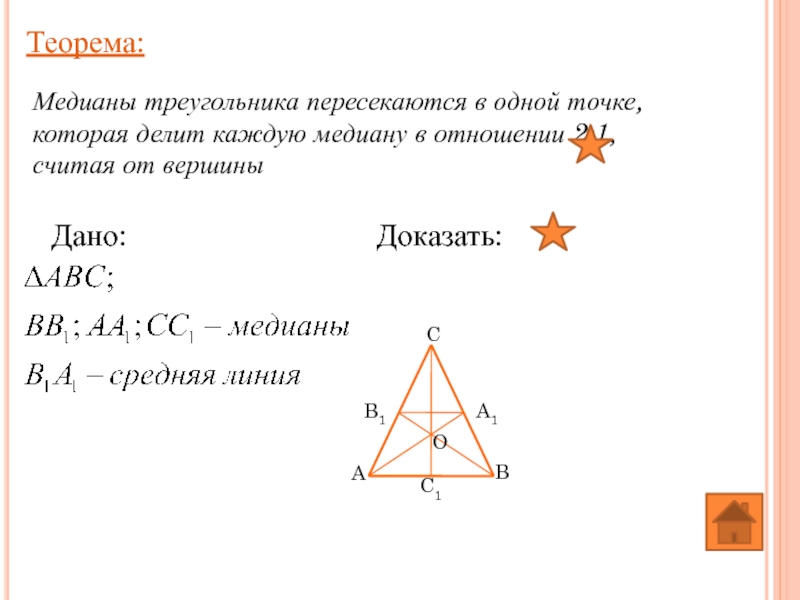
Слайд 28Теорема:
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в
отношении 2:1, считая от вершины
Дано:
Доказать:
Слайд 31
В треугольнике АВС медианы АА1 и ВВ1 пересекаются в точке О.
Найдите площадь треугольника АВС, если площадь треугольника АВО равна S
Слайд 32Теорема:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на
два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику
Дано:
Доказать:
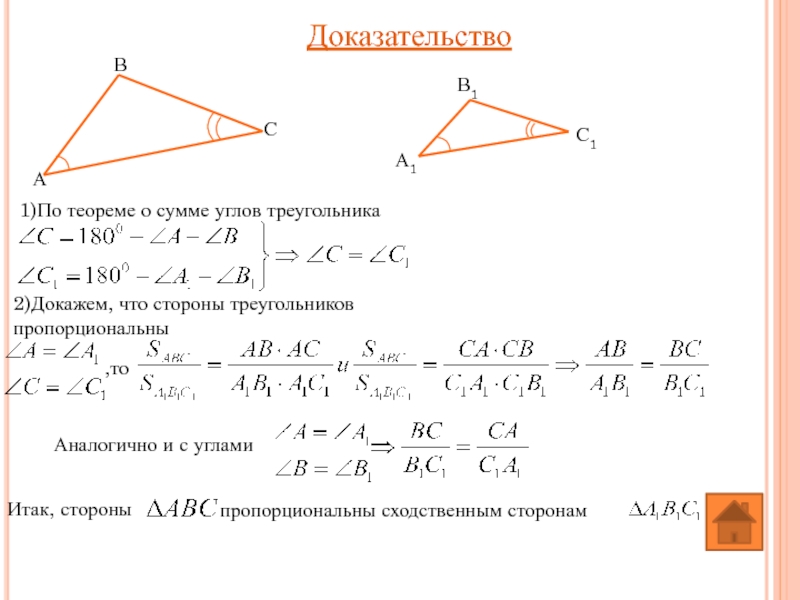
Доказательство
Слайд 33Теорема:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное
для отрезков, на которые делится гипотенуза этой высотой
Дано:
Доказать:
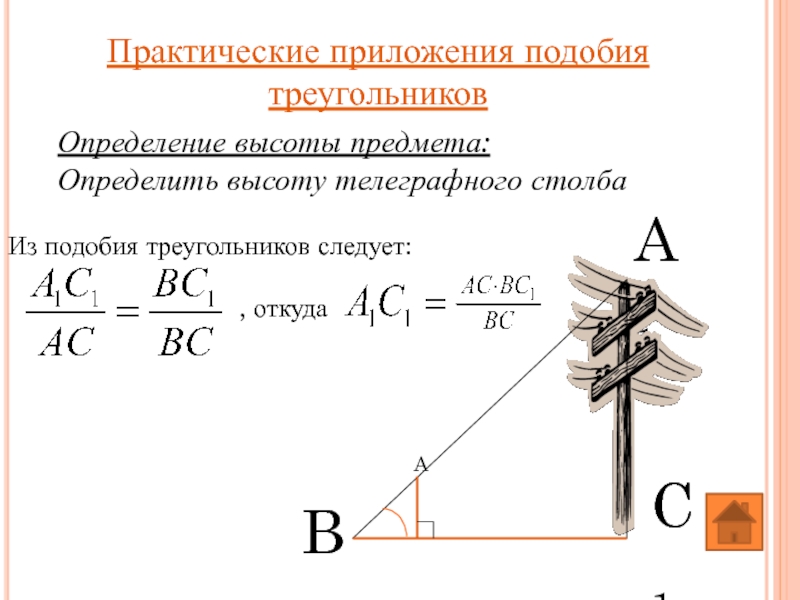
Слайд 35Определение высоты предмета:
Определить высоту телеграфного столба
Практические приложения подобия треугольников
Слайд 40
Для определения расстояния от точки А до недопустимой точки В на
местности выбрали точку С и измерили отрезок АС, углы ВАС и АСВ. Затем построили на бумаге треугольник А1В1С1, подобный треугольнику АВС. Найдите АВ, если АС=42 м, А1С1=6,3 см,А1В1=7,2 см
Слайд 42Синус, косинус и тангенс острого угла прямоугольного треугольника
Косинус - отношение
прилежащего катета к гипотенузе в прямоугольном треугольнике
Синус- отношение противолежащего катета к гипотенузе в прямоугольном треугольнике
Тангенс- отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике
