Якобовский М.В., д.ф.-м.н.
Институт математического моделирования РАН, Москва
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Учебный курс Введение в параллельные алгоритмы презентация
Содержание
- 1. Учебный курс Введение в параллельные алгоритмы
- 2. Введение в параллельные алгоритмы: Сортировка
- 3. Объём оперативной памяти одного процессорного узла достаточен
- 4. Расположить N элементов массива a таким образом,
- 5. Пусть массив можно разместить на p процессорах.
- 6. Части массива хранятся на нескольких процессорах Каждая
- 7. Будем рассматривать только процесс упорядочивания элементов: Перед
- 8. Упорядочивание фрагментов массива на каждом из
- 9. ? Конструирование наилучшего последовательного алгоритма Введение в
- 10. Сравнение алгоритмов
- 11. Пусть f(N)
- 12. Константа времени сортировки T=10-9K N
- 13. T=10-9K n log2(n) M=10-9R n log2(n) Пирамидальная
- 14. Введение в параллельные алгоритмы: Сортировка данных
- 15. сортировать ( массив mas, число элементов n
- 16. Dsort(intsort *array, int n) { a=array; // сортируемый массив b=array_second; // вспомогательный массив for(i=1;i
- 17. Слияние упорядоченных фрагментов for(ia=0,ib=0,k=0;k=n1) b[j+k]=a[r+ib++]; else if(ib>=n2) b[j+k]=a[j+ia++]; else if(a[j+ia]
- 18. Требуется 2 + 4 + 8 +
- 19. Ускорение при методе сдваивания Введение в
- 20. Требуется 8 тактов Слияние двух массивов двумя
- 21. Дерево называют сбалансированным, если потомки любого его
- 22. Не пирамида Москва, 2009 г. Введение
- 23. Пирамида Москва, 2009 г. Введение в
- 24. В линейном массиве потомки вершины i хранятся
- 25. 2 3 5 1 4 3 7
- 26. Пирамида называется упорядоченной если
- 27. 9 5 8 4 4
- 28. 9 5 8 4 4
- 29. 9 5 8 4 4
- 30. Оптимальный алгоритм Оптимальна комбинация H алгоритма
- 31. Введение в параллельные алгоритмы: Сортировка данных
- 32. Рассмотрен ряд методов сортировки массивов Проиллюстрирована
- 33. В чем причина различия характера зависимости времени
- 34. Якобовский М.В. д.ф.-м.н., зав. сектором
Слайд 1Лекция 3
Сортировка данных с точки зрения МВС
(начало)
Учебный курс
Введение в параллельные
алгоритмы
Слайд 2
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало)
© Якобовский М.В.
Ц Е Л Ь
О С Н О В Н А Я
Расположить в порядке
неубывания
N элементов массива чисел,
используя p процессоров
Москва, 2009 г.
из 34
Слайд 3Объём оперативной памяти одного процессорного узла достаточен для одновременного размещения в
ней всех элементов массива
Объём оперативной памяти одного процессорного узла мал для одновременного размещения в ней всех элементов массива
Объём оперативной памяти одного процессорного узла мал для одновременного размещения в ней всех элементов массива
Две задачи сортировки массива чисел
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 4Расположить N элементов массива a таким образом, чтобы для любого выполнялось
неравенство
Задача А
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 5Пусть массив можно разместить на p процессорах.
Пусть на процессоре с
номером rank размещено
элементов массива .
Расположить N элементов массивов таким образом, чтобы:
для любых и выполнялось неравенство
для любого
выполнялось неравенство
Расположить N элементов массивов таким образом, чтобы:
для любых и выполнялось неравенство
для любого
выполнялось неравенство
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 6Части массива хранятся на нескольких процессорах
Каждая часть массива должна быть упорядочена
На
процессорах с большими номерами должны быть размещены элементы массива с большими значениями
Правильно
Ошибка
Ошибка
Правильно
Ошибка
Ошибка
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 7Будем рассматривать только процесс упорядочивания элементов:
Перед началом сортировки на каждом из
процессоров уже есть часть элементов массива
После окончания сортировки на каждом из процессоров должно остаться столько элементов, сколько их было в начале (но, это уже могут быть другие элементы, расположенные ранее на других процессорах)
После окончания сортировки на каждом из процессоров должно остаться столько элементов, сколько их было в начале (но, это уже могут быть другие элементы, расположенные ранее на других процессорах)
Задача B
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 8
Упорядочивание фрагментов массива на каждом из процессоров ?
Перераспределение элементов массива между
процессорами
Упорядочивание фрагментов массива на каждом из процессоров ?
Упорядочивание фрагментов массива на каждом из процессоров ?
Этапы сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 9?
Конструирование наилучшего последовательного алгоритма
Введение в параллельные алгоритмы: Сортировка данных с точки
зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 10
Сравнение алгоритмов сортировки
Введение в параллельные алгоритмы: Сортировка данных с точки зрения
МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Слайд 11Пусть f(N)
в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 12Константа времени сортировки
T=10-9K N log2(N)
Введение в параллельные алгоритмы: Сортировка данных
с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
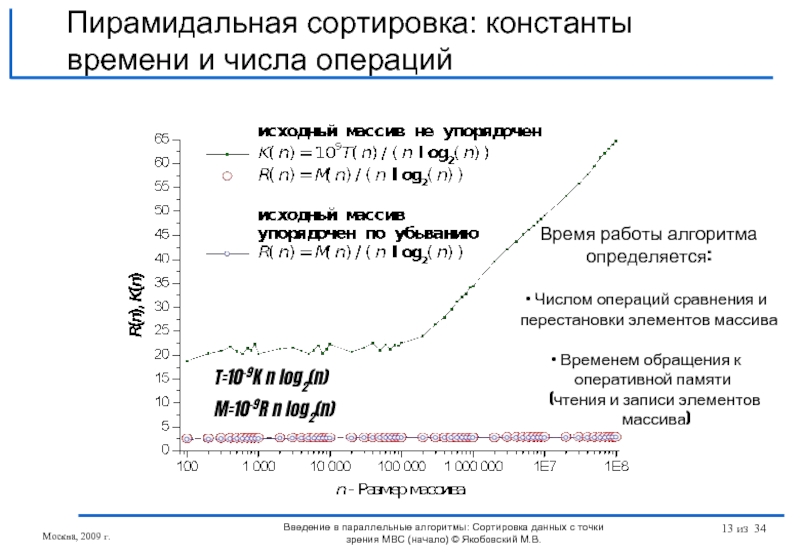
Слайд 13T=10-9K n log2(n)
M=10-9R n log2(n)
Пирамидальная сортировка: константы времени и числа операций
Введение
в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Время работы алгоритма определяется:
Числом операций сравнения и перестановки элементов массива
Временем обращения к
оперативной памяти
(чтения и записи элементов
массива)
из 34
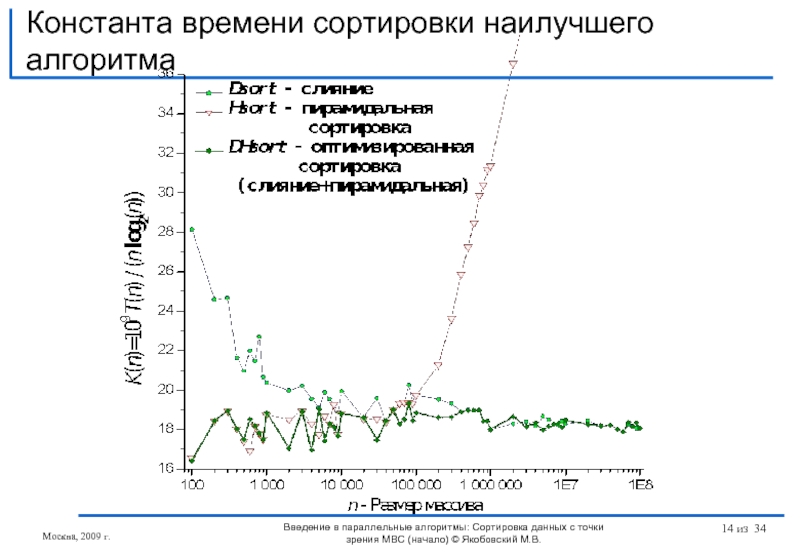
Слайд 14
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало)
© Якобовский М.В.
Москва, 2009 г.
Константа времени сортировки наилучшего алгоритма
из 34
Слайд 15сортировать ( массив mas, число элементов n )
{
если (n
> 1)
{
// сортировка первой половины массива
сортировать ( mas, n/2);
// сортировка второй половины массива
сортировать ( mas+n/2, n-n/2);
// слияние отсортированных половинок массива
слияние ( mas, n/2, mas+n/2,n-n/2);
}
}
{
// сортировка первой половины массива
сортировать ( mas, n/2);
// сортировка второй половины массива
сортировать ( mas+n/2, n-n/2);
// слияние отсортированных половинок массива
слияние ( mas, n/2, mas+n/2,n-n/2);
}
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Изящный алгоритм сортировки массива слиянием
из 34
Слайд 16Dsort(intsort *array, int n)
{
a=array; // сортируемый массив
b=array_second; // вспомогательный массив
for(i=1;i
// размер объединяемых фрагментов
{
for(j=0;j // фрагментов
{
r=j+i; // начало второго из объединяемых фрагментов
n1=max(min(i,n-j), 0);
n2=max(min(i,n-r), 0);
// слияние упорядоченных фрагментов
b = a[r…r+n1] & a[j…j+n2]
}
c=a;a=b;b=c;
}
{
for(j=0;j
{
r=j+i; // начало второго из объединяемых фрагментов
n1=max(min(i,n-j), 0);
n2=max(min(i,n-r), 0);
// слияние упорядоченных фрагментов
b = a[r…r+n1] & a[j…j+n2]
}
c=a;a=b;b=c;
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
Алгоритм сортировки массива слиянием
из 34
Слайд 17Слияние упорядоченных фрагментов
for(ia=0,ib=0,k=0;k=n1) b[j+k]=a[r+ib++];
else
if(ib>=n2) b[j+k]=a[j+ia++];
else
if(a[j+ia]
b[j+k]=a[r+ib++];
}
}
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 18Требуется 2 + 4 + 8 + 16 тактов (8 процессоров)
Сортировка
слиянием методом сдваивания
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Для просмотра анимации возможно требуется установить свободно распространяемый Swiff Point Player: http://www.globfx.com/products/swfpoint/
Слайд 19Ускорение при методе сдваивания
Введение в параллельные алгоритмы: Сортировка данных с точки
зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
k1 – сортировка, k2 – передача данных
из 34
Слайд 20Требуется 8 тактов
Слияние двух массивов двумя процессорами
Москва, 2009 г.
Введение в параллельные
алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
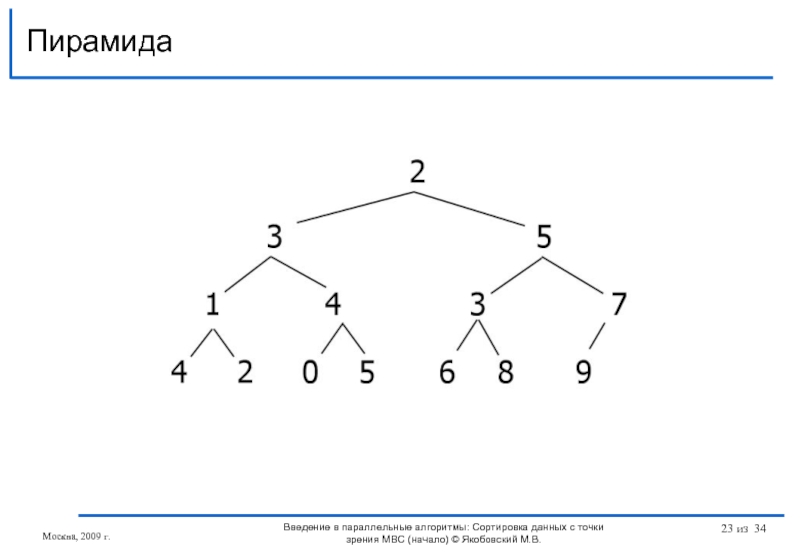
Слайд 21Дерево называют сбалансированным, если потомки любого его корня отличаются по высоте
не более чем на 1
Пирамида – сбалансированное бинарное дерево в котором левый потомок любого узла не ниже правого потомка
Пирамида – сбалансированное бинарное дерево в котором левый потомок любого узла не ниже правого потомка
Пирамиды
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Слайд 22
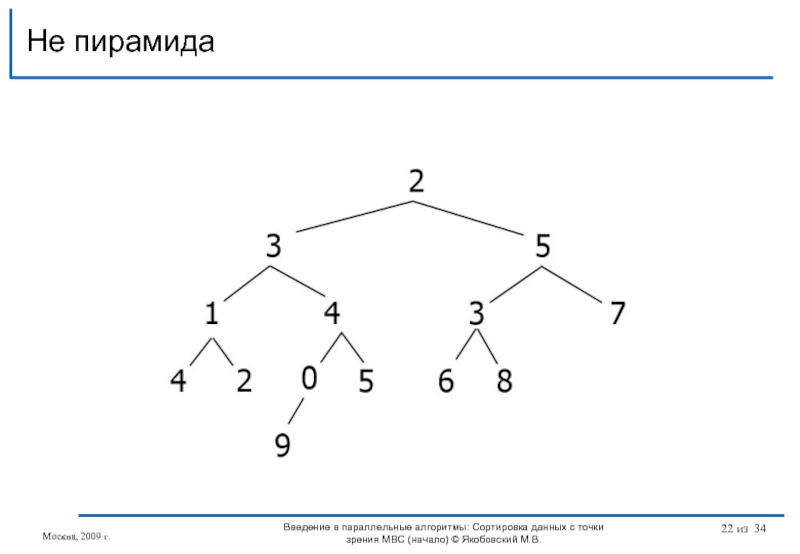
Не пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки
зрения МВС (начало) © Якобовский М.В.
из 34
Слайд 23
Пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения
МВС (начало) © Якобовский М.В.
из 34
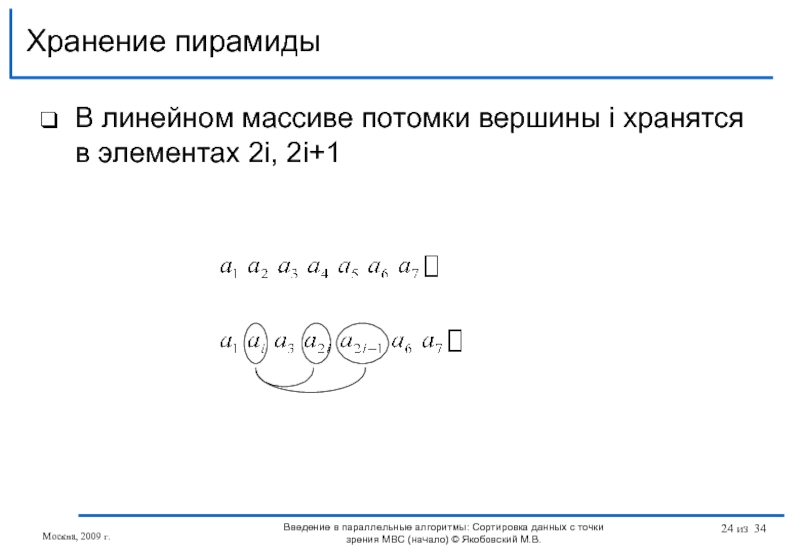
Слайд 24В линейном массиве потомки вершины i хранятся в элементах 2i, 2i+1
Хранение
пирамиды
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
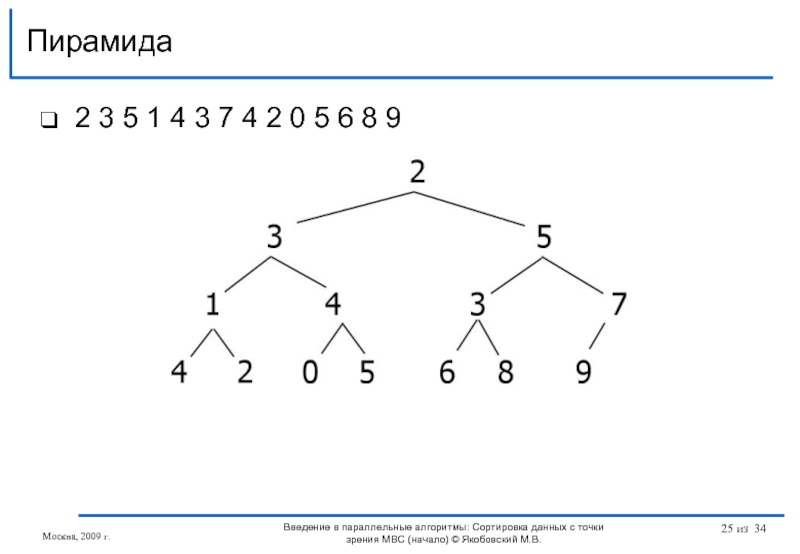
Слайд 252 3 5 1 4 3 7 4 2 0 5
6 8 9
Пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Слайд 26
Пирамида называется упорядоченной если
для любого
(если такие элементы в массиве
есть ☺)
Пирамидальная сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
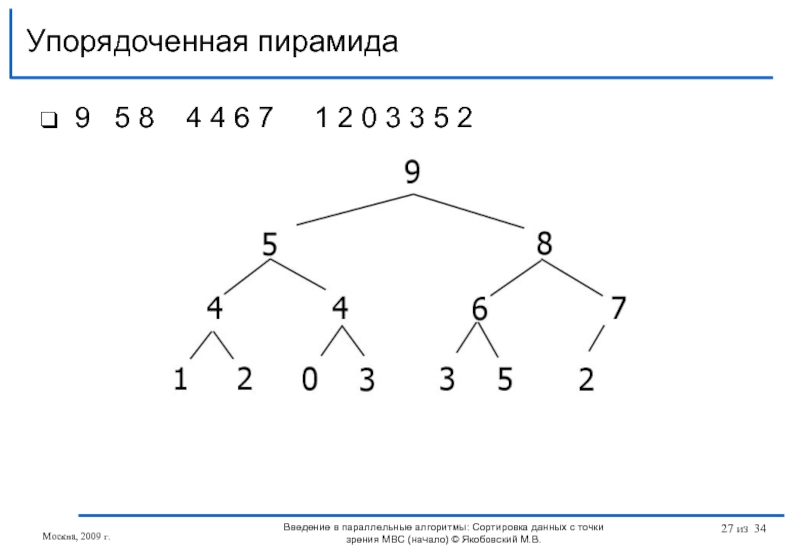
Слайд 279 5 8 4 4 6 7
1 2 0 3 3 5 2
Упорядоченная пирамида
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Слайд 289 5 8 4 4 6 7
1 2 0 3 3 5 2 [
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
3 5 6 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 5 4 4 3 2 1 2 0 3 [ 7 8 9
3 5 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 3 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 4 5 3 4 3 2 1 2 0 [ 6 7 8 9
0 4 5 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 0 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 3 3 4 0 2 1 2 [ 5 6 7 8 9
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
3 5 6 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 3 4 4 5 2 1 2 0 3 [ 7 8 9
6 5 5 4 4 3 2 1 2 0 3 [ 7 8 9
3 5 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 3 5 4 4 3 2 1 2 0 [ 6 7 8 9
5 4 5 3 4 3 2 1 2 0 [ 6 7 8 9
0 4 5 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 0 3 4 3 2 1 2 [ 5 6 7 8 9
5 4 3 3 4 0 2 1 2 [ 5 6 7 8 9
Пирамидальная
сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
2 4 3 3 4 0 2 1 [ 5 5 6 7 8 9
4 2 3 3 4 0 2 1 [ 5 5 6 7 8 9
4 4 3 3 2 0 2 1 [ 5 5 6 7 8 9
1 2 3 3 4 0 2 [ 4 5 5 6 7 8 9
1 2 3 3 4 0 2 [ 4 5 5 6 7 8 9
3 2 1 3 4 0 2 [ 4 5 5 6 7 8 9
3 2 2 3 4 0 1 [ 4 5 5 6 7 8 9
1 2 2 3 4 0 [ 3 4 5 5 6 7 8 9
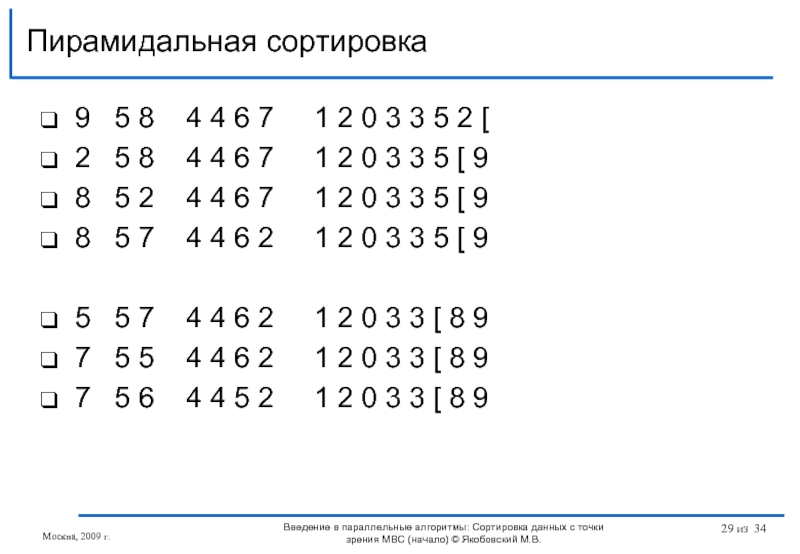
Слайд 299 5 8 4 4 6 7
1 2 0 3 3 5 2 [
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
2 5 8 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 2 4 4 6 7 1 2 0 3 3 5 [ 9
8 5 7 4 4 6 2 1 2 0 3 3 5 [ 9
5 5 7 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 5 4 4 6 2 1 2 0 3 3 [ 8 9
7 5 6 4 4 5 2 1 2 0 3 3 [ 8 9
Пирамидальная сортировка
Москва, 2009 г.
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
из 34
Слайд 30Оптимальный алгоритм
Оптимальна комбинация
H алгоритма (пирамидальная )
в диапазоне
10 - 50 000
D алгоритма (слияние) в диапазоне
50 000 - 100 000 000
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
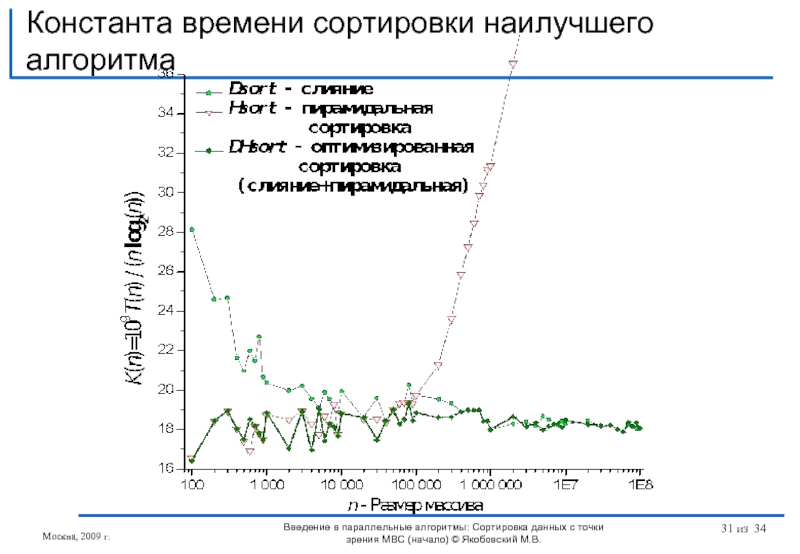
Слайд 31
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало)
© Якобовский М.В.
Москва, 2009 г.
Константа времени сортировки наилучшего алгоритма
из 34
Слайд 32Рассмотрен ряд методов сортировки массивов
Проиллюстрирована разница между зависимостью от объема
данных времени сортировки и числа выполняемых операций
Построен «наилучший» последовательный алгоритм сортировки
Построен «наилучший» последовательный алгоритм сортировки
Заключение
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 33В чем причина различия характера зависимости времени сортировки и числа выполняемых
операций от числа элементов сортируемого массива?
Какие еще можно предложить варианты сортировки, улучшающие использование кеш- памяти?
Какие еще можно предложить варианты сортировки, улучшающие использование кеш- памяти?
Вопросы для обсуждения
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
Слайд 34Якобовский М.В.
д.ф.-м.н.,
зав. сектором
«Программного обеспечения многопроцессорных систем и вычислительных
сетей»
Института математического моделирования
Российской академии наук
mail: mail: lira@imamod.rumail: lira@imamod.ru
web: web: http://lira.imamod.ru
Института математического моделирования
Российской академии наук
mail: mail: lira@imamod.rumail: lira@imamod.ru
web: web: http://lira.imamod.ru
Контакты
Введение в параллельные алгоритмы: Сортировка данных с точки зрения МВС (начало) © Якобовский М.В.
Москва, 2009 г.
из 34
