- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
§3. Параллелограмм. Средняя линия треугольника. презентация
Содержание
- 1. §3. Параллелограмм. Средняя линия треугольника.
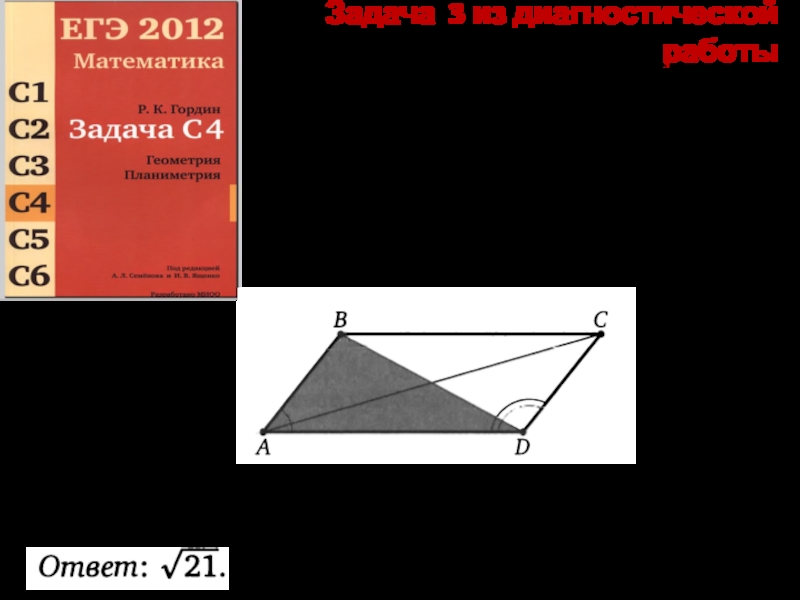
- 2. Задача 3 из диагностической работы
- 3. Для решения задач этого раздела нужно знать
- 4. ПРИМЕР 1. В выпуклом четырёхугольнике
- 5. ПРИМЕР 2. В выпуклом четырёхугольнике ABCD длина
- 6. ПРИМЕР 3. Вершины одного параллелограмма лежат
- 7. 7 подготовительных задач 3.1. Расстояние между
- 8. 7 подготовительных задач 3.4. Сторона ВС
- 9. 7 подготовительных задач 3.6. В четырёхугольнике
Слайд 3Для решения задач этого раздела нужно знать
свойства и признаки параллелограмма,
теорему о средней линии треугольника,
теорему о медианах треугольника (медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника),
Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Теорема. Середины сторон любого четырёхугольника являются вершинами параллелограмма.
Слайд 4ПРИМЕР 1.
В выпуклом четырёхугольнике отрезки, соединяющие середины противоположных сторон, равны
Найдите диагонали четырёхугольника.
Роспись за запись решения на доске
Идея решения. По диагоналям параллелограмма найти его стороны – это половины диагоналей данного четырехугольника
Слайд 5ПРИМЕР 2. В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины сторон АВ
Ответ:
Оригинальный способ решения :
найти параллелограмм!!!
1
Р
Слайд 6ПРИМЕР 3. Вершины одного параллелограмма лежат по одной на сторонах другого.
Оригинальный способ решения :
найти параллелограмм!!!
Слайд 77 подготовительных задач 3.1. Расстояние между серединами взаимно перпендикулярных хорд АС и
Балл за решение каждой задачи
Слайд 87 подготовительных задач 3.4. Сторона ВС параллелограмма ABCD вдвое больше стороны АВ.
Балл за решение каждой задачи
Слайд 97 подготовительных задач
3.6. В четырёхугольнике ABCD известны углы: ∠DAB=90°, ∠ DBC=
Кроме того, DB = a, DC = b.
Найдите расстояние между центрами двух окружностей, одна из которых
проходит через точки D, А, В,
а другая — через точки B,C,D.
3.7. На сторонах АВ и CD прямоугольника ABCD
взяты точки К и М так, что АКСМ — ромб.
Диагональ АС образует со стороной АВ угол 30°.
Найдите сторону ромба, если наибольшая сторона прямоугольника ABCD равна 3.
Балл за решение каждой задачи