- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аттестационная работа. Способы решения квадратных уравнений презентация
Содержание
- 1. Аттестационная работа. Способы решения квадратных уравнений
- 3. Теория уравнений занимает ведущее место в алгебре
- 4. Цель Задачи выявить способы решения
- 8. История возникновения квадратных уравнений Др.Индия 499 г. Др. Вавилон Европа 13 – 17 в. Диофант
- 9. Способы решения квадратных уравнений Разложение левой
- 10. Свойства:
- 11. Умножив обе
- 12. Данный способ заключается в
- 13. Это старый и незаслуженно
- 14. Рассмотрим, как древние греки
- 15. Разложение левой части уравнения
- 16. Ответ: -4,5; 1. По
- 17. Ответ: -4,5; 1.
- 18. Ответ: -4,5; 1. Графический
- 19. Ответ: -4,5; 1. С
- 20. Одни квадратные уравнения можно решить разными способами,
- 22. Плужников И.10 способов решения квадратных уравнений//Математика в
Слайд 3Теория уравнений занимает ведущее место в алгебре и математике в целом.
Слайд 4Цель
Задачи
выявить способы решения квадратных уравнений, узнать можно ли решить любое квадратное
проанализировать источники литературы для выявления способов решения квадратных уравнений, показать различные способы решения квадратных уравнений.
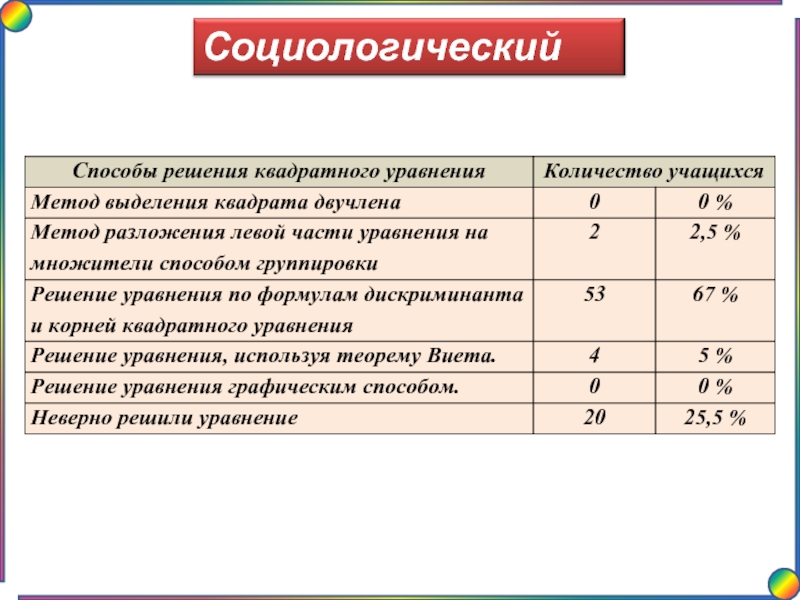
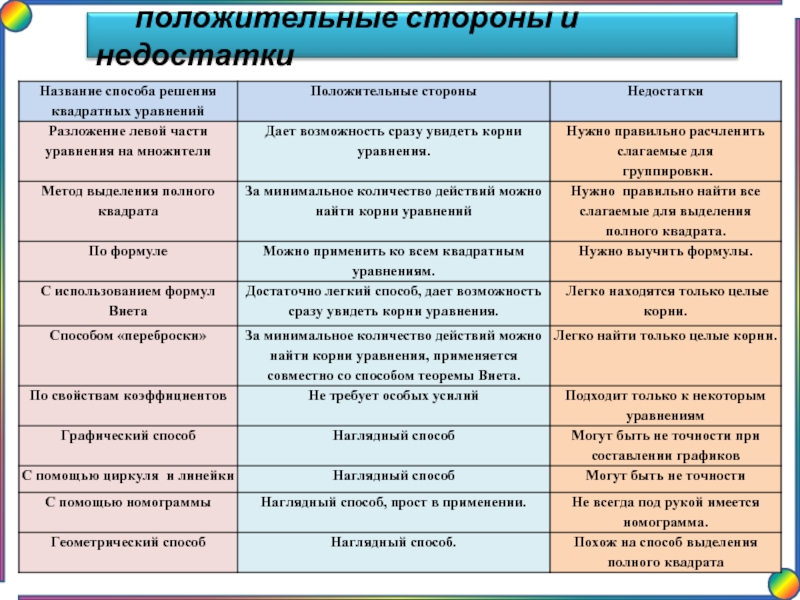
Слайд 9Способы решения квадратных уравнений
Разложение левой части на множители
Метод выделения полного квадрата
По
С использованием теоремы Виета (прямой и обратной)
Способом «переброски»
По свойствам коэффициентов
Графический способ
С помощью циркуля и линейки
С помощью номограммы
Геометрический способ
Основные
Дополнительные
Слайд 11
Умножив обе части уравнения на а, получим
Пусть
,
Тогда получим уравнение с новой переменной
Его корни у1 и у2. Окончательно
Слайд 12
Данный способ заключается в том, чтобы при нахождении корней уравнения
и А(0;1); провести окружность с центром в точке S и радиусом SA. Абсциссы точек пересечения с осью Ох есть корни исходного уравнения
Слайд 13
Это старый и незаслуженно забытый способ решения квадратных уравнений. Номограмма взята
Для этого надо на оси р взять точку M с координатой р, на оси q – точку N с координатой q и провести прямую MN. Каждая точка пересечения прямой MN с кривой Г даѐт положительный корень уравнения.
Построенная прямая MN может пересекаться с кривой Г:
в двух точках (в этом случае оба корня данного уравнения положительны);
в одной точке (в этом случае второй корень уравнения отрицателен);
может касаться кривой (в этом случае у уравнения кратный положительный корень);
может не иметь с кривой Г ни одной общей точки (в этом случае либо оба корня уравнения отрицательны, либо у него вообще нет действительных корней).
Слайд 14
Рассмотрим, как древние греки решали уравнение
Решение представлено на рисунке, где
Выражения
геометрически представляют собой один и тот же квадрат со стороной 5. Поэтому
или
и 16 + 9
Слайд 15
Разложение левой части
уравнения на множители
Ответ: -4,5; 1.
Метод выделения
полного квадрата
Слайд 16
Ответ: -4,5; 1.
По формуле
С использованием
формул Виета
имеет два разных
по
больший по модулю
корень отрицательный
Слайд 17
Ответ: -4,5; 1.
Способом «переброски»
По свойству коэффициентов
Перебросим коэффициент а =
из которого по формулам Виета
Корнями исходного уравнения будут
Так как
то
Слайд 18
Ответ: -4,5; 1.
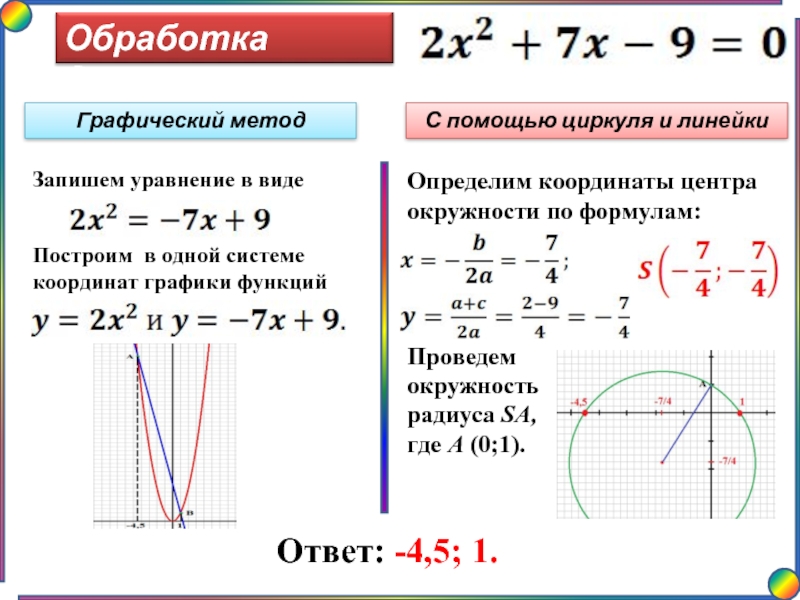
Графический метод
С помощью циркуля и линейки
Запишем уравнение в виде
Построим в одной системе координат графики функций
Определим координаты центра окружности по формулам:
Проведем окружность радиуса SA, где А (0;1).
Слайд 19
Ответ: -4,5; 1.
С помощью номограммы
Геометрический способ
Представим уравнение в виде:
Номограмма дает положительный
отрицательный корень
Представим уравнение в виде:
Площадь полученного квадрата:
Так как
, то:
Таким образом, получили уравнение:
Слайд 20Одни квадратные уравнения можно решить разными способами, а для других уравнений
Основным в решении квадратных уравнений является правильно выбрать рациональный способ решения и применить алгоритм решения
Данные способы решения заслуживают внимания, поскольку они не все отражены в школьных учебниках математики. Овладение данными способами поможет учащимся экономить время и эффективно решать уравнения, так как потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.
Слайд 22Плужников И.10 способов решения квадратных уравнений//Математика в школе.-2004.-№41
Гусев В. А., Мордкович
Глейзер Г. И. История математики в школе. – М.: просвещение, 1982
Брадис В. М. Четырехзначные математические таблицы для средней школы. – м., просвещение, 1990
Дидактические материалы по алгебре.
http://revolution.allbeс.ru/
http://mat.1september.ru/2004/41/no42_01.htm