Курс: DVM-технология разработки параллельных программ для вычислительных кластеров презентация

Содержание

Содержание Прошлое MPI – модель передачи сообщений DVM – модель параллелизма по данным и управлению. Язык Си-DVM Настоящее Многоядерные и многопоточные процессоры. SMP-кластеры Гибридная модель программирования MPI/OpenMP Язык Fortran-DVM/OpenMP Будущее Гибридные

Слайд 1Курс: «DVM-технология разработки параллельных программ для вычислительных кластеров»
Бахтин Владимир Александрович
К.ф.-м.н., зав.

сектором Института прикладной математики им М.В.Келдыша РАН
Ассистент кафедры системного программирования факультета ВМК Московского государственного университета им. М.В. Ломоносова
bakhtin@keldysh.ru

Слайд 2Содержание
Прошлое
MPI – модель передачи сообщений
DVM – модель параллелизма по данным и

управлению. Язык Си-DVM
Настоящее
Многоядерные и многопоточные процессоры. SMP-кластеры
Гибридная модель программирования MPI/OpenMP
Язык Fortran-DVM/OpenMP
Будущее
Гибридные вычислительные кластеры
PGI Accelerator Model
Язык Fortran-DVM/OpenMP/Accelerator


25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 3Алгоритм Якоби. Последовательная версия
/* Jacobi program */
#include
#define L 1000
#define ITMAX

100
int i,j,it;
double A[L][L];
double B[L][L];
int main(int an, char **as)
{
printf("JAC STARTED\n");
for(i=0;i<=L-1;i++)
for(j=0;j<=L-1;j++)
{
A[i][j]=0.;
B[i][j]=1.+i+j;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 4Алгоритм Якоби. Последовательная версия
/****** iteration loop *************************/

for(it=1; it {
for(i=1;i<=L-2;i++)
for(j=1;j<=L-2;j++)
A[i][j] = B[i][j];
for(i=1;i<=L-2;i++)
for(j=1;j<=L-2;j++)
B[i][j] = (A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4.;
}
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

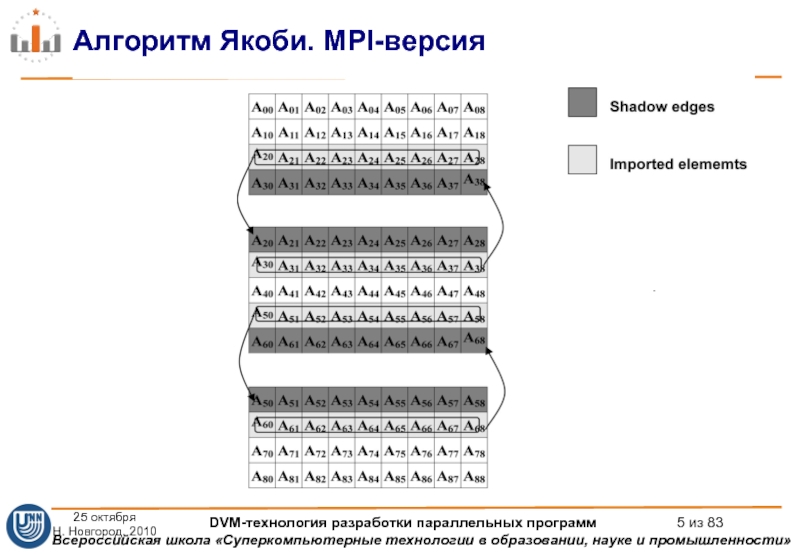
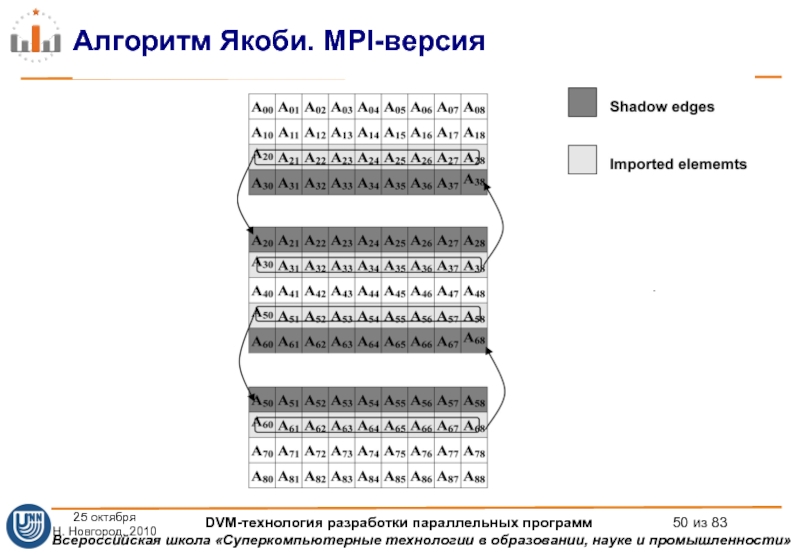
Слайд 5Алгоритм Якоби. MPI-версия
25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных

программ из 83

Слайд 6Алгоритм Якоби. MPI-версия
/* Jacobi-1d program */
#include
#include
#include
#include "mpi.h"
#define m_printf

if (myrank==0)printf
#define L 1000
#define ITMAX 100

int i,j,it,k;
int ll,shift;
double (* A)[L];
double (* B)[L];


25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 7Алгоритм Якоби. MPI-версия
int main(int argc, char **argv)
{
MPI_Request req[4];
int myrank, ranksize;
int startrow,lastrow,nrow;
MPI_Status

status[4];
double t1, t2, time;
MPI_Init (&argc, &argv); /* initialize MPI system */
MPI_Comm_rank(MPI_COMM_WORLD, &myrank);/*my place in MPI system*/
MPI_Comm_size (MPI_COMM_WORLD, &ranksize); /* size of MPI system */
MPI_Barrier(MPI_COMM_WORLD);
/* rows of matrix I have to process */
startrow = (myrank *L) / ranksize;
lastrow = (((myrank + 1) * L) / ranksize)-1;
nrow = lastrow - startrow + 1;
m_printf("JAC1 STARTED\n");

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 8Алгоритм Якоби. MPI-версия
/* dynamically allocate data structures */
A = malloc ((nrow+2)

* L * sizeof(double));
B = malloc ((nrow) * L * sizeof(double));
for(i=1; i<=nrow; i++)
for(j=0; j<=L-1; j++)
{
A[i][j]=0.;
B[i-1][j]=1.+startrow+i-1+j;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 9Алгоритм Якоби. MPI-версия
/****** iteration loop *************************/
t1=MPI_Wtime();

for(it=1; it<=ITMAX; it++)
{
for(i=1; i<=nrow; i++)
{
if (((i==1)&&(myrank==0))||((i==nrow)&&(myrank==ranksize-1))) continue;
for(j=1; j<=L-2; j++)
{
A[i][j] = B[i-1][j];
}
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 10Алгоритм Якоби. MPI-версия
if(myrank!=0)
MPI_Irecv(&A[0][0],L,MPI_DOUBLE, myrank-1, 1235,

MPI_COMM_WORLD, &req[0]);
if(myrank!=ranksize-1)
MPI_Isend(&A[nrow][0],L,MPI_DOUBLE, myrank+1, 1235,
MPI_COMM_WORLD,&req[2]);
if(myrank!=ranksize-1)
MPI_Irecv(&A[nrow+1][0],L,MPI_DOUBLE, myrank+1, 1236,
MPI_COMM_WORLD, &req[3]);
if(myrank!=0)
MPI_Isend(&A[1][0],L,MPI_DOUBLE, myrank-1, 1236,
MPI_COMM_WORLD,&req[1]);
ll=4; shift=0;
if (myrank==0) {ll=2;shift=2;}
if (myrank==ranksize-1) {ll=2;}
MPI_Waitall(ll,&req[shift],&status[0]);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 11Алгоритм Якоби. MPI-версия
for(i=1; i

it*/
printf("%d: Time of task=%lf\n",myrank,MPI_Wtime()-t1);
MPI_Finalize ();
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 12Алгоритм Якоби. DVM-версия
#include
#define L 1000
#define ITMAX 100
int i,j,it;
#define DVM(dvmdir)
#define DO(v,l,h,s)

for(v=(l); v<=(h); v+=(s))
DVM(DISTRIBUTE [BLOCK][BLOCK]) double A[L][L];
DVM(ALIGN [i][j] WITH A[i][j]) double B[L][L];
int main(int an, char **as)
{
printf("JAC STARTED\n");
DVM(PARALLEL [i][j] ON A[i][j])
DO(i,0,L-1,1)
DO(j,0,L-1,1)
{
A[i][j]=0.;
B[i][j]=1.+i+j;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 13Алгоритм Якоби. DVM-версия
/****** iteration loop *************************/

for(it=1; it {
DVM(PARALLEL [i][j] ON A[i][j])
DO(i,1,L-2,1)
DO(j,1,L-2,1)
A[i][j] = B[i][j];
DVM(PARALLEL [i][j] ON B[i][j]; SHADOW_RENEW A)
DO(i,1,L-2,1)
DO(j,1,L-2,1)
B[i][j] = (A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4.;
}
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 14Модель параллелизма по данным и управлению. DVM
Эта модель (1993 г.), положенная

в основу языков параллельного программирования Фортран-DVM и Си-DVM, объединяет достоинства модели параллелизма по данным и модели параллелизма по управлению
Базирующаяся на этих языках система разработки параллельных программ (DVM) создана в ИПМ им. М.В. Келдыша РАН
Аббревиатура DVM (Distributed Virtual Memory, Distributed Virtual Machine) отражает поддержку виртуальной общей памяти на распределенных системах

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 15Модель программирования DVM
на программиста возлагается ответственность за соблюдение правила собственных вычислений


программист определяет общие (удаленные) данные, т.е. данные, вычисляемые на одних процессорах и используемые на других процессорах
программист отмечает точки в последовательной программе, где происходит обновление значений общих данных
программист распределяет по процессорам виртуальной параллельной машины не только данные, но и соответствующие вычисления

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 16Состав DVM-системы
DVM-система состоит из следующих компонент:
Компилятор Fortran-DVM/OpenMP
Компилятор C-DVM
Библиотека поддержки LIB-DVM
DVM-отладчик
Предсказатель выполнения

DVM-программ
Анализатор производительности DVM-программ

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 17Средства программирования
C-DVM = Язык Си + специальные макросы
Fortran-DVM/OpenMP = Язык Фортран

95 + специальные комментарии
Специальные комментарии и макросы являются высокоуровневыми спецификациями параллелизма в терминах последовательной программы
Отсутствуют низкоуровневые передачи данных и синхронизации
Последовательный стиль программирования
Спецификации параллелизма «невидимы» для стандартных компиляторов
Существует только один экземпляр программы для последовательного и параллельного счета

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

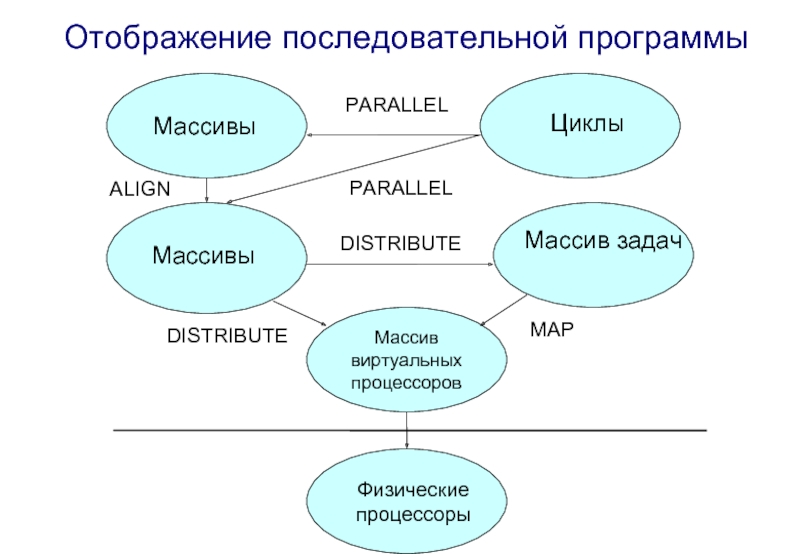
Слайд 18





Массив
виртуальных
процессоров

Массивы
Массивы
Циклы

Массив задач

Физические
процессоры
PARALLEL
PARALLEL
ALIGN
DISTRIBUTE
DISTRIBUTE
MAP
Отображение последовательной программы

Слайд 19Распределение данных. DISTRIBUTE
DVM( DISTRIBUTE f1…fk )
где fi = [ BLOCK

] - распределение равными блоками (распределенное измерение)
[MULT_BLOCK(m)] - распределение блоками кратными m (распределенное измерение)
[GENBLOCK ( block-array-name )] - распределение блоками указанных размеров
[WGTBLOCK ( block-array-name,nblock )] - распределение взвешенными блоками
[ ] - распределение целым измерением (локальное измерение)
k - количество измерений массива

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 20Распределение данных. DISTRIBUTE

DVM(DISTRIBUTE [BLOCK]) double A[12];

DVM(DISTRIBUTE [BLOCK]) double B[6];
DVM(DISTRIBUTE [MULT_BLOCK(3)]) double A[12];
node1 node2 node3 node4
A 0,1,2 3,4,5 6,7,8 9,10,11
B 0,1 2,3 4 5

double wb[6]={1.,0.5,0.5,0.5,0.5,1.};
int bs[4]={2,4,4,2};
DVM(DISTRIBUTE [GEN_BLOCK(bs)]) double A[12];
DVM(DISTRIBUTE [WGT_BLOCK(wb,6)]) double B[6];

node1 node2 node3 node4
A 0,1 2,3,4,5 6,7,8,9 10,11
B 0 1,2 3,4 5

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 21Распределение данных. DISTRIBUTE
DVM(DISTRIBUTE [BLOCK] [ ] [BLOCK]) float A[N][N][N];
…
dvm run M1 M2

<имя-программы> /*P(M1,M2)*/

Директива распределяет первое измерение массива А на первое измерение P блоками размера N/M1, третье измерение А - на второе измерение P блоками размера N/M2, а второе измерение А будет целиком распределено на каждый виртуальный процессор.

#define DVM(dvmdir)

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 22Распределение вычислений вне параллельных циклов

Одна ОПМД-программа выполняется на всех
процессорах с локальным

подмножеством
данных
Правило собственных вычислений:
OWN(A[i]) - процессор, на который распределен A[i]
A[i] = expri
Оператор всегда выполняется на процессоре OWN(A[i])
Проба: свой - “чужой” оператор по правилу собственных вычислений

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 23Локализация данных. ALIGN

DVM(DISTRIBUTE B[BLOCK][BLOCK]) float B[N][M+1];
. . .
for

(i=0; i for(j=0; j {
B[i][j+1] = A[i][j];
}

DVM(ALIGN [i][j] WITH B[i][j+1]) float A[N][M];

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 24Локализация данных. ALIGN
DVM(ALIGN a1… an WITH B b1… bm )

<описание-массива-A-на-языке-Си>
где ai - параметр i–го измерения выравниваемого массива А
bj - параметр j–го измерения базового массива B
n - количество измерений массива А
m - количество измерений массива В
ai =[ IDi ] bj =[ c*IDj+d ]
=[ ] =[ ]
где IDi , IDj - идентификаторы
c, d - целочисленные константы

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 25Локализация данных. ALIGN
DVM(ALIGN [i] WITH B[2*i+1] ) float A[N];
Распределить элемент A[

i ] и B[2*i+1] на один процессор.
DVM(ALIGN [i][j] WITH B[j][i]) float A[N][N];
Распределить элемент A[ i ] [ j ] и B[ j ] [ i ] на один процессор.
DVM(ALIGN [i] WITH B[][i]) float A[N];
Распределить элемент A[ i ] на те процессоры, где размещен хотя бы один элемент i-ого столбца B.
DVM(ALIGN [i] [ ] WITH B[i]) float A[N][N];
Распределить i-ую строку A и элемент B[ i ] на один процессор, т.е. размножить второе измерение массива А.

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 26Распределение витков цикла. PARALLEL
Заголовки параллельного цикла не должны разделяться другими операторами

(тесно-гнездовой цикл);
Параметры заголовков параллельного цикла не должны изменяться в процессе выполнения цикла (прямоугольное индексное пространство);
Виток цикла должен быть неделимым объектом и выполняться на одном процессоре. Поэтому левые части операторов присваивания одного витка цикла должны быть распределены на один процессор (согласование с правилом собственных вычислений).

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 27Распределение витков цикла. PARALLEL
FOR(i, N)
{
D[2*i] = …;
D[2*i+1]

= …;
}

DVM(PARALLEL [i] ON D[2*i])
FOR(i, N)
{
D[2*i] = …;
}
DVM(PARALLEL [i] ON D[2*i+1])
FOR(i, N)
{
D[2*i+1] = …;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 28Локализация данных. TEMPLATE

DVM(PARALLEL [i] ON A[i])
FOR(i, N)
{
A[i] = B[i+d1]

+ C[i-d2];
}

DVM(DISTRIBUTE [BLOCK]; TEMPLATE [N+d1+d2]) void *TABC;
DVM( ALIGN [i] WITH TABC[i] ) float B[N];
DVM( ALIGN [i] WITH TABC[i+d2] ) float A[N];
DVM( ALIGN [i] WITH TABC[i+d1+d2] ) float C[N];

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 29Удаленные данные типа SHADOW

DVM(DISTRIBUTE [BLOCK]) float A[N];
DVM(PARALLEL [i] ON A[i]; SHADOW_RENEW

B )
FOR(i, N)
{
A[i] = B[i+d1] + B[i-d2];
}

DVM( ALIGN [i] WITH A[i]; SHADOW [d1:d2] ) float B[N];


25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 30Удаленные данные типа SHADOW

DVM(DISTRIBUTE [BLOCK][BLOCK]) float C[100][100];
DVM(ALIGN[I][J] WITH C[I][J]) float A[100][100],

B[100][100], D[100][100];
DVM(SHADOW_GROUP) void *AB;
. . .
DVM(CREATE_SHADOW_GROUP AB: A B);
. . .
DVM(SHADOW_START AB);
. . .
DVM(PARALLEL[I][J] ON C[I][J]; SHADOW_WAIT AB)
DO( I, 1, 98, 1)
DO( J, 1, 98, 1) {
C[I][J] = (A[I-1][J]+A[I+1][J]+A[I][J-1]+A[I][J+1])/4.;
D[I][J] = (B[I-1][J]+B[I+1][J]+B[I][J-1]+B[I][J+1])/4.;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 31Удаленные данные типа ACROSS

DVM(DISTRIBUTE [BLOCK]; SHADOW [d1:d2] ) float A[N];
DVM(PARALLEL [i]

ON A[i] ]; ACROSS A[d1:d2])
FOR(i, N)
{
A[i] = A[i+d1] + A[i-d2];
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 32Удаленные данные типа REMOTE

DVM(DISTRIBUTE [BLOCK]) float A[N];
DVM(PARALLEL [i] ON A[i]; REMOTE_ACCESS

C[5] C[i+n])
FOR(i, N)
{
A[i] = C[5] + C[i+n];
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 33Удаленные данные типа REMOTE
DVM (DISTRIBUTE [BLOCK][BLOCK]) float A1[M][N1+1], A2[M1+1][[N2+1], A3[M2+1][N2+1];
DVM (REMOTE_GROUP)

void *RS;
DO(ITER,1, MIT,1) {
. . .
DVM (PREFETCH RS);
. . .
DVM ( PARALLEL[i] ON A1[i][N1]; REMOTE_ACCESS RS: A2[i][1])
DO(i,0, M1-1,1)
A1[i][N1] = A2[i][1];
DVM (PARALLEL[i] ON A1[i][N1]; REMOTE_ACCESS RS: A3[i-M1][1])
DO(i,M1, M-1,1)
A1[i][N1] = A3[i-M1][1];
DVM (PARALLEL[i] ON A2[i][0]; REMOTE_ACCESS RS: A1[I][N1-1])
DO(i,0, M1-1,1)
A2[i][0] = A1[i][N1-1];
DVM(PARALLEL[i] ON A3[i][0]; REMOTE_ACCESS RS: A1[I+M1][N1-1])
DO (i,0, M2-1,1)
A3[i][0] = A1[i+M1][N1-1];
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 34Удаленные данные типа REDUCTION

DVM(DISTRIBUTE [BLOCK]) float A[N];
DVM(PARALLEL [i] ON A[i] ;

REDUCTION SUM(S) )
FOR(i, N)
{
A[i] = B[i] + C[i];
s = s + A[i];
}

DVM( ALIGN [i] WITH A[i]) float B[N];
DVM( ALIGN [i] WITH A[i]) float C[N];

К редукционным операторам относятся:
SUM, PRODUCT, AND, OR, MAX, MIN, MAXLOC, MINLOC

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 35Удаленные данные типа REDUCTION
DVM(REDUCTION_GROUP) void *RG;
S = 0; X = A[1];

Y = A[1]; MINI = 1;
DVM(PARALLEL[I] ON A[I]; REDUCTION RG: SUM(S), MAX(X), MINLOC(Y,MIMI))
FOR(I, N) {
S = S + A[I];
X =max(X, A[I]);
if(A[I] < Y) {
Y = A[I];
MINI = I;
}
}
DVM(REDUCTION_START RG);
DVM(PARALLEL[I] ON B[I])
FOR( I, N)
B[I] = C[I] + A[I];
DVM(REDUCTION_WAIT RG);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 36Копирование секций массивов

DVM(DISTRIBUTE [BLOCK][]) float A[N][N];
DVM(ALIGN [i][j] WITH [j][i]) float B[N][N];

. . .
DVM(COPY)
FOR(i,N)
FOR(j,N)
B[i][j]=A[i][j];

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 37Копирование секций массивов

DVM(DISTRIBUTE [BLOCK][]) float A[N][N];
DVM(ALIGN [i][j] WITH [j][i]) float B[N][N];

. . .
DVM(COPY_FLAG) void * flag;
. . .
DVM(COPY_START &flag)
FOR(i,N)
FOR(j,N)
B[i][j]=A[i][j];
. . .
DVM(COPY_WAIT &flag);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

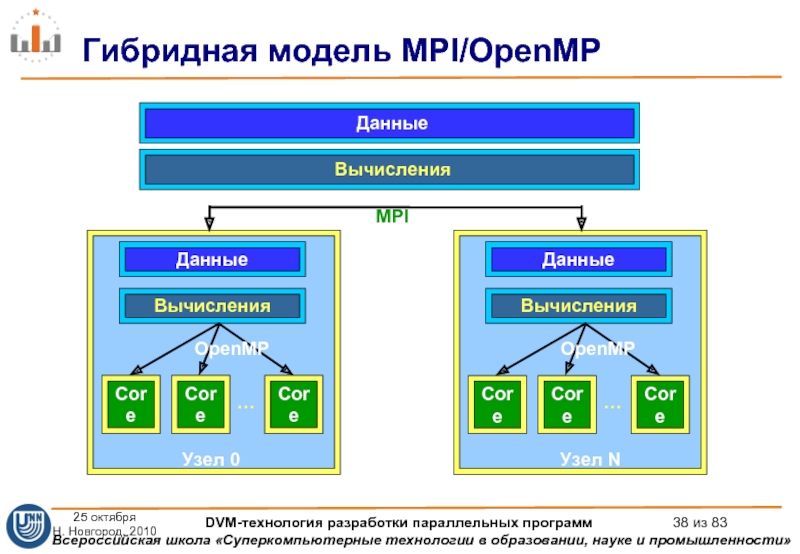
Слайд 38Гибридная модель MPI/OpenMP


Данные



Данные

Вычисления
…
Узел N
OpenMP


Вычисления
MPI
25 октября
Н. Новгород, 2010
DVM-технология разработки

параллельных программ из 83

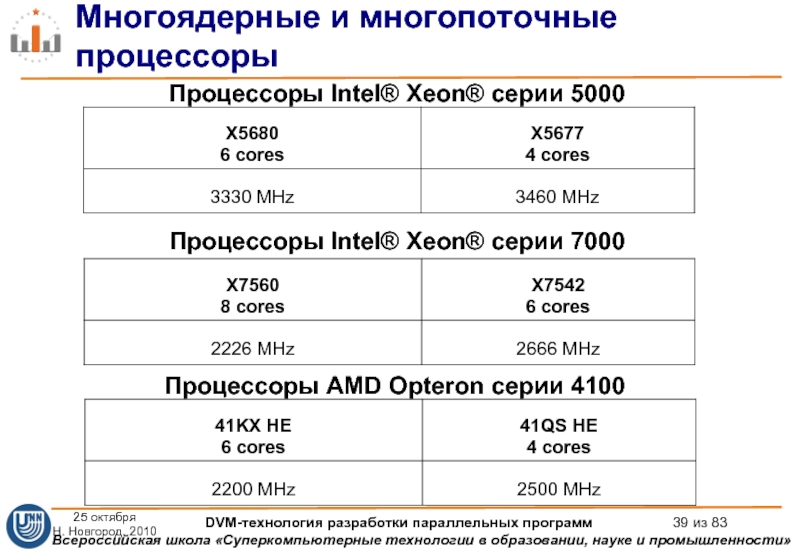
Слайд 39Многоядерные и многопоточные процессоры

Процессоры Intel® Xeon® серии 5000
Процессоры Intel® Xeon® серии

7000

Процессоры AMD Opteron серии 4100

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 40Достоинства использования в узлах OpenMP вместо MPI
Возможность инкрементального распараллеливания.
Упрощение программирования и

эффективность на нерегулярных вычислениях, проводимых над общими данными.
Ликвидация или сокращение дублирования данных в памяти, свойственного MPI-программам.
Дополнительный уровень параллелизма на OpenMP реализовать проще, чем на MPI.

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 41Преимущества OpenMP для многоядерных процессоров
Объемы оперативной памяти и кэш памяти, приходящиеся

в среднем на одно ядро, будут сокращаться – присущая OpenMP экономия памяти становится очень важна.
Ядра используют общую Кэш-память, что требуется учитывать при оптимизации программы.

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 42National Institute for Computational Sciences. University of Tennessee
Суперкомпьютер Kraken Cray XT5-HE

Opteron Six Core 2.6 GHz
4 место в TOP 500

http://nics.tennessee.edu

Пиковая производительность - 1028.85 TFlop/s
Число процессоров/ядер в системе — 16 288 / 98 928
Производительность на Linpack - 831.7 TFlop/s (81% от пиковой)


Updrage: замена 4-х ядерных процессоров AMD Opteron на 6-ти ядерные процессоры AMD Opteron
Результат: 6-ое место в TOP500 в июне 2009 - 3-ье место в TOP500 в ноябре 2009

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 43National Institute for Computational Sciences. University of Tennessee

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 44Межведомственный Суперкомпьютерный Центр Российской Академии Наук
Суперкомпьютер MVS-100K
46 место в TOP 500

http://www.jscc.ru/

Пиковая

производительность - 140.16 TFlop/s
Число процессоров/ядер в системе — 2 920/11 680
Производительность на Linpack - 107.45 TFlop/s (76.7% от пиковой)


Updrage: замена 2-х ядерных процессоров Intel Xeon 53xx на 4-х ядерные процессоры Intel Xeon 54xx
Результат: 57-ое место в TOP500 в июне 2008 - 36-ое место в TOP500 в ноябре 2008

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 45Oak Ridge National Laboratory
Суперкомпьютер Jaguar Cray XT5-HE Opteron Six Core 2.6

GHz
1 место в TOP 500

http://computing.ornl.gov

Пиковая производительность - 2331 TFlop/s
Число ядер в системе — 224 162
Производительность на Linpack - 1759 TFlop/s (75.4% от пиковой)


Updrage: замена 4-х ядерных процессоров AMD Opteron на 6-ти ядерные процессоры AMD Opteron
Результат: 2-ое место в TOP500 в июне 2009 - 1-ое место в TOP500 в ноябре 2009

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

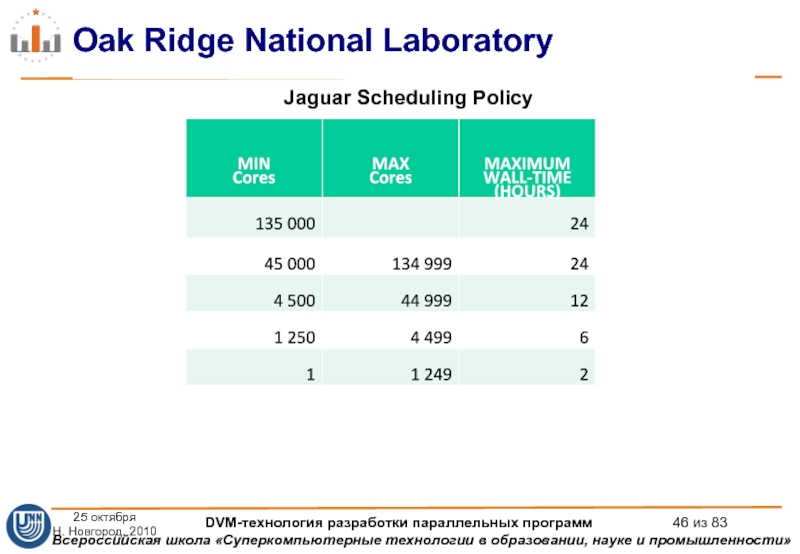
Слайд 46Oak Ridge National Laboratory
Jaguar Scheduling Policy
25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

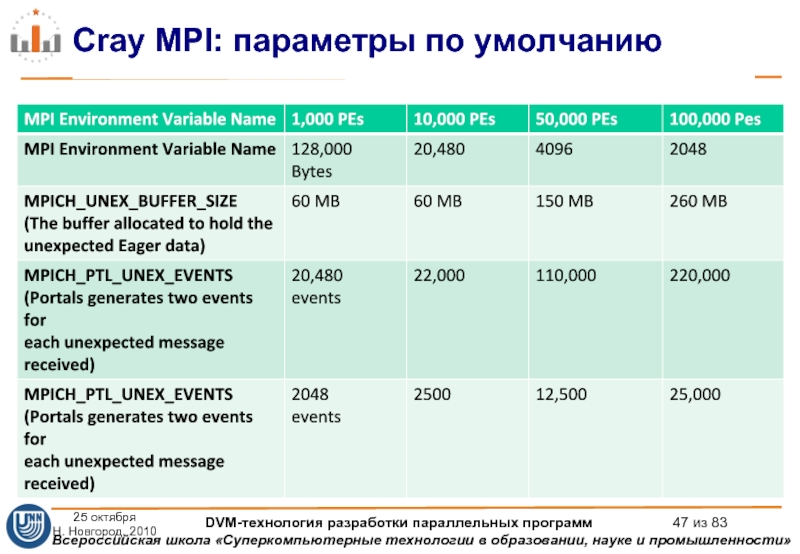
Слайд 47Cray MPI: параметры по умолчанию
25 октября
Н. Новгород, 2010
DVM-технология

разработки параллельных программ из 83

Слайд 48Алгоритм Якоби. Последовательная версия
/* Jacobi program */
#include
#define L 1000
#define ITMAX

100
int i,j,it;
double A[L][L];
double B[L][L];
int main(int an, char **as)
{
printf("JAC STARTED\n");
for(i=0;i<=L-1;i++)
for(j=0;j<=L-1;j++)
{
A[i][j]=0.;
B[i][j]=1.+i+j;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 49Алгоритм Якоби. Последовательная версия
/****** iteration loop *************************/

for(it=1; it {
for(i=1;i<=L-2;i++)
for(j=1;j<=L-2;j++)
A[i][j] = B[i][j];
for(i=1;i<=L-2;i++)
for(j=1;j<=L-2;j++)
B[i][j] = (A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4.;
}
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 50Алгоритм Якоби. MPI-версия
25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных

программ из 83

Слайд 51Алгоритм Якоби. MPI-версия
/* Jacobi-1d program */
#include
#include
#include
#include "mpi.h"
#define m_printf

if (myrank==0)printf
#define L 1000
#define ITMAX 100

int i,j,it,k;
int ll,shift;
double (* A)[L];
double (* B)[L];


25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 52Алгоритм Якоби. MPI-версия
int main(int argc, char **argv)
{
MPI_Request req[4];
int myrank, ranksize;
int startrow,lastrow,nrow;
MPI_Status

status[4];
double t1, t2, time;
MPI_Init (&argc, &argv); /* initialize MPI system */
MPI_Comm_rank(MPI_COMM_WORLD, &myrank);/*my place in MPI system*/
MPI_Comm_size (MPI_COMM_WORLD, &ranksize); /* size of MPI system */
MPI_Barrier(MPI_COMM_WORLD);
/* rows of matrix I have to process */
startrow = (myrank *L) / ranksize;
lastrow = (((myrank + 1) * L) / ranksize)-1;
nrow = lastrow - startrow + 1;
m_printf("JAC1 STARTED\n");

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 53Алгоритм Якоби. MPI-версия
/* dynamically allocate data structures */
A = malloc ((nrow+2)

* L * sizeof(double));
B = malloc ((nrow) * L * sizeof(double));
for(i=1; i<=nrow; i++)
for(j=0; j<=L-1; j++)
{
A[i][j]=0.;
B[i-1][j]=1.+startrow+i-1+j;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 54Алгоритм Якоби. MPI-версия
/****** iteration loop *************************/
t1=MPI_Wtime();

for(it=1; it<=ITMAX; it++)
{
for(i=1; i<=nrow; i++)
{
if (((i==1)&&(myrank==0))||((i==nrow)&&(myrank==ranksize-1))) continue;
for(j=1; j<=L-2; j++)
{
A[i][j] = B[i-1][j];
}
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 55Алгоритм Якоби. MPI-версия
if(myrank!=0)
MPI_Irecv(&A[0][0],L,MPI_DOUBLE,

myrank-1, 1235,
MPI_COMM_WORLD, &req[0]);
if(myrank!=ranksize-1)
MPI_Isend(&A[nrow][0],L,MPI_DOUBLE, myrank+1, 1235,
MPI_COMM_WORLD,&req[2]);
if(myrank!=ranksize-1)
MPI_Irecv(&A[nrow+1][0],L,MPI_DOUBLE, myrank+1, 1236, MPI_COMM_WORLD, &req[3]);
if(myrank!=0)
MPI_Isend(&A[1][0],L,MPI_DOUBLE, myrank-1, 1236, MPI_COMM_WORLD,&req[1]);
ll=4; shift=0;
if (myrank==0) {ll=2;shift=2;}
if (myrank==ranksize-1) {ll=2;}
MPI_Waitall(ll,&req[shift],&status[0]);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 56Алгоритм Якоби. MPI-версия
for(i=1; i

it*/
printf("%d: Time of task=%lf\n",myrank,MPI_Wtime()-t1);
MPI_Finalize ();
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

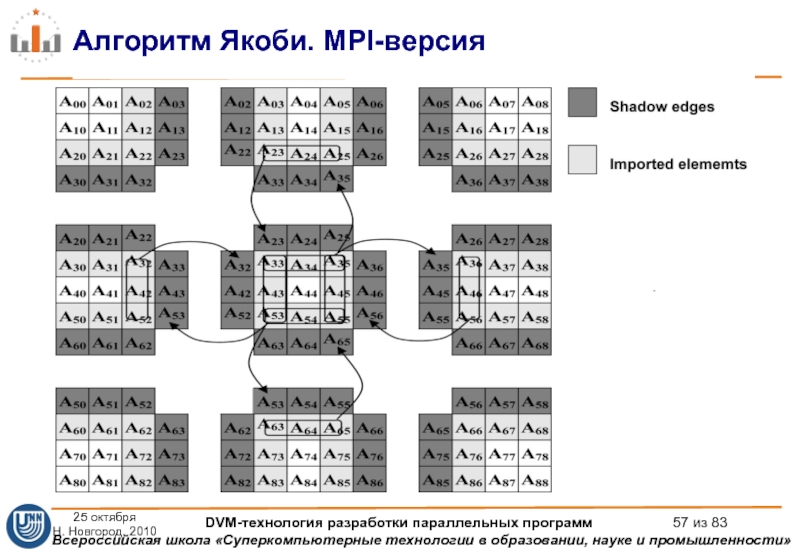
Слайд 57Алгоритм Якоби. MPI-версия
25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных

программ из 83

Слайд 58Алгоритм Якоби. MPI-версия
/*Jacobi-2d program */
#include
#include
#include
#include "mpi.h"
#define m_printf if

(myrank==0)printf
#define L 1000
#define LC 2
#define ITMAX 100

int i,j,it,k;

double (* A)[L/LC+2];
double (* B)[L/LC];

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 59Алгоритм Якоби. MPI-версия
int main(int argc, char **argv)
{
MPI_Request req[8];
int myrank, ranksize;
int srow,lrow,nrow,scol,lcol,ncol;
MPI_Status

status[8];
double t1;
int isper[] = {0,0};
int dim[2];
int coords[2];
MPI_Comm newcomm;
MPI_Datatype vectype;
int pleft,pright, pdown,pup;
MPI_Init (&argc, &argv); /* initialize MPI system */
MPI_Comm_size (MPI_COMM_WORLD, &ranksize); /* size of MPI system */
MPI_Comm_rank (MPI_COMM_WORLD, &myrank); /* my place in MPI system */

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 60Алгоритм Якоби. MPI-версия
dim[0]=ranksize/LC;
dim[1]=LC;
if ((L%dim[0])||(L%dim[1]))
{
m_printf("ERROR: array[%d*%d] is not distributed on %d*%d processors\n",L,L,dim[0],dim[1]);
MPI_Finalize();
exit(1);
}
MPI_Cart_create(MPI_COMM_WORLD,2,dim,isper,1,&newcomm);
MPI_Cart_shift(newcomm,0,1,&pup,&pdown);
MPI_Cart_shift(newcomm,1,1,&pleft,&pright);
MPI_Comm_rank

(newcomm, &myrank); /* my place in MPI system */
MPI_Cart_coords(newcomm,myrank,2,coords);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 61Алгоритм Якоби. MPI-версия
/* rows of matrix I have to process */
srow

= (coords[0] * L) / dim[0];
lrow = (((coords[0] + 1) * L) / dim[0])-1;
nrow = lrow - srow + 1;
/* columns of matrix I have to process */
scol = (coords[1] * L) / dim[1];
lcol = (((coords[1] + 1) * L) / dim[1])-1;
ncol = lcol - scol + 1;
MPI_Type_vector(nrow,1,ncol+2,MPI_DOUBLE,&vectype);
MPI_Type_commit(&vectype);
m_printf("JAC2 STARTED on %d*%d processors with %d*%d array, it=%d\n",dim[0],dim[1],L,L,ITMAX);
/* dynamically allocate data structures */
A = malloc ((nrow+2) * (ncol+2) * sizeof(double));
B = malloc (nrow * ncol * sizeof(double));

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 62Алгоритм Якоби. MPI-версия
for(i=0; i


for(it=1; it<=ITMAX; it++)
{
for(i=0; i<=nrow-1; i++)
{
if (((i==0)&&(pup==MPI_PROC_NULL))||((i==nrow-1)&&(pdown==MPI_PROC_NULL))) continue;
for(j=0; j<=ncol-1; j++)
{
if (((j==0)&&(pleft==MPI_PROC_NULL))||((j==ncol-1)&&(pright==MPI_PROC_NULL)))
continue;
A[i+1][j+1] = B[i][j];
}
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 63Алгоритм Якоби. MPI-версия
MPI_Irecv(&A[0][1],ncol,MPI_DOUBLE,
pup, 1235, MPI_COMM_WORLD, &req[0]);
MPI_Isend(&A[nrow][1],ncol,MPI_DOUBLE,

pdown, 1235, MPI_COMM_WORLD,&req[1]);
MPI_Irecv(&A[nrow+1][1],ncol,MPI_DOUBLE,
pdown, 1236, MPI_COMM_WORLD, &req[2]);
MPI_Isend(&A[1][1],ncol,MPI_DOUBLE,
pup, 1236, MPI_COMM_WORLD,&req[3]);
MPI_Irecv(&A[1][0],1,vectype,
pleft, 1237, MPI_COMM_WORLD, &req[4]);
MPI_Isend(&A[1][ncol],1,vectype,
pright, 1237, MPI_COMM_WORLD,&req[5]);
MPI_Irecv(&A[1][ncol+1],1,vectype,
pright, 1238, MPI_COMM_WORLD, &req[6]);
MPI_Isend(&A[1][1],1,vectype,
pleft, 1238, MPI_COMM_WORLD,&req[7]);
MPI_Waitall(8,req,status);

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 64Алгоритм Якоби. MPI-версия
for(i=1; i

(((i==1)&&(pup==MPI_PROC_NULL))||
((i==nrow)&&(pdown==MPI_PROC_NULL))) continue;
for(j=1; j<=ncol; j++)
{
if (((j==1)&&(pleft==MPI_PROC_NULL))||
((j==ncol)&&(pright==MPI_PROC_NULL))) continue;
B[i-1][j-1] = (A[i-1][j]+A[i+1][j]+A[i][j-1]+A[i][j+1])/4.;
}
}
}
printf("%d: Time of task=%lf\n",myrank,MPI_Wtime()-t1);
MPI_Finalize ();
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 65Алгоритм Якоби. MPI/OpenMP-версия
/****** iteration loop *************************/
t1=MPI_Wtime();
#pragma omp parallel default(none) private(it,i,j) shared

(A,B,myrank, nrow,ranksize,ll,shift,req,status)
for(it=1; it<=ITMAX; it++)
{
for(i=1; i<=nrow; i++)
{
if (((i==1)&&(myrank==0))||((i==nrow)&&(myrank==ranksize-1))) continue;
#pragma omp for nowait
for(j=1; j<=L-2; j++)
{
A[i][j] = B[i-1][j];
}
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 66Алгоритм Якоби. MPI/OpenMP-версия
#pragma omp barrier
#pragma omp single
{
if(myrank!=0)
MPI_Irecv(&A[0][0],L,MPI_DOUBLE, myrank-1, 1235, MPI_COMM_WORLD, &req[0]);
if(myrank!=ranksize-1)
MPI_Isend(&A[nrow][0],L,MPI_DOUBLE,

myrank+1, 1235, MPI_COMM_WORLD,&req[2]);
if(myrank!=ranksize-1)
MPI_Irecv(&A[nrow+1][0],L,MPI_DOUBLE, myrank+1, 1236, MPI_COMM_WORLD, &req[3]);
if(myrank!=0)
MPI_Isend(&A[1][0],L,MPI_DOUBLE, myrank-1, 1236, MPI_COMM_WORLD,&req[1]);
ll=4; shift=0; if (myrank==0) {ll=2;shift=2;}
if (myrank==ranksize-1) {ll=2;}
MPI_Waitall(ll,&req[shift],&status[0]);
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 67Алгоритм Якоби. MPI/OpenMP-версия
for(i=1; i

j++)
B[i-1][j] = (A[i-1][j]+A[i+1][j]+
A[i][j-1]+A[i][j+1])/4.;
}
}/*DO it*/
printf("%d: Time of task=%lf\n",myrank,MPI_Wtime()-t1);
MPI_Finalize ();
return 0;
}

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

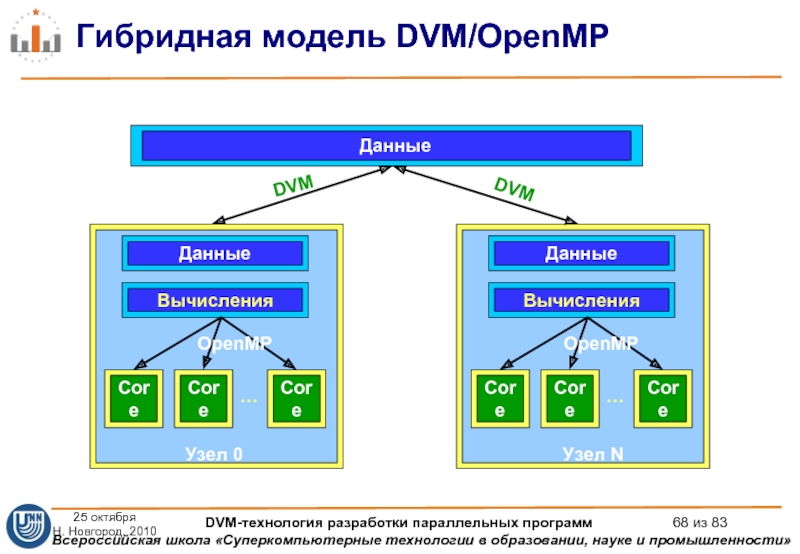
Слайд 68Гибридная модель DVM/OpenMP



Данные



Данные

Вычисления
…
Узел N
OpenMP
DVM
DVM
25 октября
Н. Новгород, 2010
DVM-технология разработки

параллельных программ из 83

Слайд 69Алгоритм Якоби. DVM/OpenMP-версия
PROGRAM

JAC_OpenMP_DVM
PARAMETER (L=1000, ITMAX=100)
REAL A(L,L), B(L,L)
CDVM$ DISTRIBUTE ( BLOCK, BLOCK) :: A
CDVM$ ALIGN B(I,J) WITH A(I,J)
PRINT *, '********** TEST_JACOBI **********'
C$OMP PARALLEL DEFAULT(NONE ) SHARED(A,B) PRIVATE(IT,I,J)
DO IT = 1, ITMAX
CDVM$ PARALLEL (J,I) ON A(I, J)
DO J = 2, L-1
C$OMP DO
DO I = 2, L-1
A(I, J) = B(I, J)
ENDDO
C$OMP ENDDO NOWAIT
ENDDO

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 70Алгоритм Якоби. DVM/OpenMP-версия
C$OMP BARRIER
CDVM$ PARALLEL

(J,I) ON B(I, J), SHADOW_RENEW (A)
DO J = 2, L-1
C$OMP DO
DO I = 2, L-1
B(I, J) = (A(I-1, J) + A(I, J-1) + A(I+1, J) + A(I, J+1)) / 4
ENDDO
C$OMP ENDDO NOWAIT
ENDDO
ENDDO
C$OMP END PARALLEL
END

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

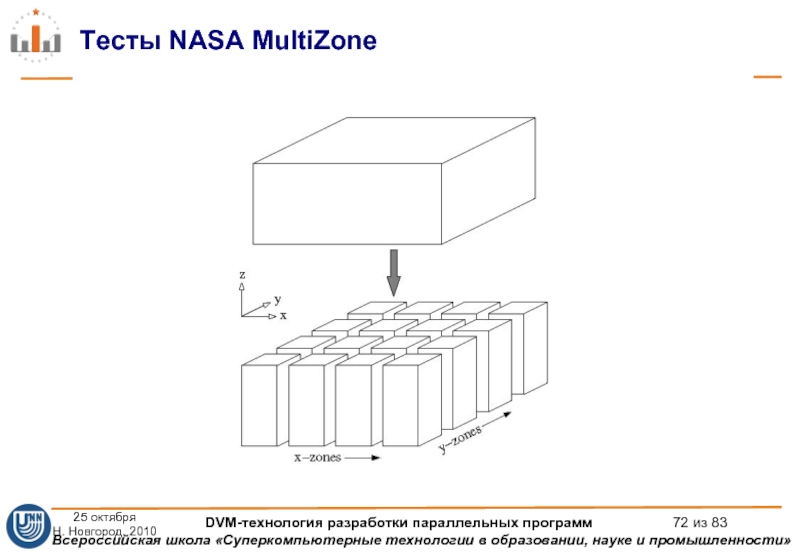
Слайд 71Тесты NASA MultiZone
BT (Block Tridiagonal Solver) 3D Навье-Стокс, метод переменных направлений
LU

(Lower-Upper Solver) 3D Навье-Стокс, метод верхней релаксации
SP (Scalar PentadiagonalSolver) 3D Навье-Стокс, Beam-Warning approximate factorization

http://www.nas.nasa.gov/News/Techreports/2003/PDF/nas-03-010.pdf

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 72Тесты NASA MultiZone


25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных

программ из 83

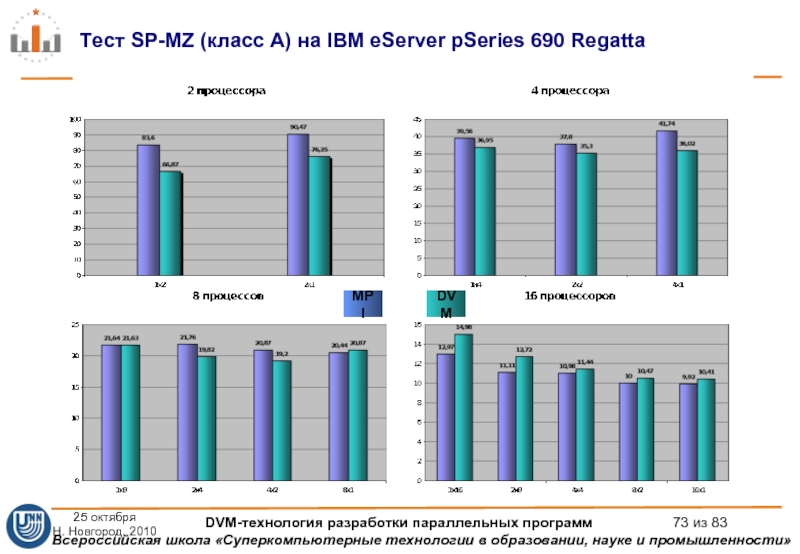
Слайд 73Тест SP-MZ (класс A) на IBM eServer pSeries 690 Regatta

DVM
MPI
25 октября
Н.

Новгород, 2010

DVM-технология разработки параллельных программ из 83

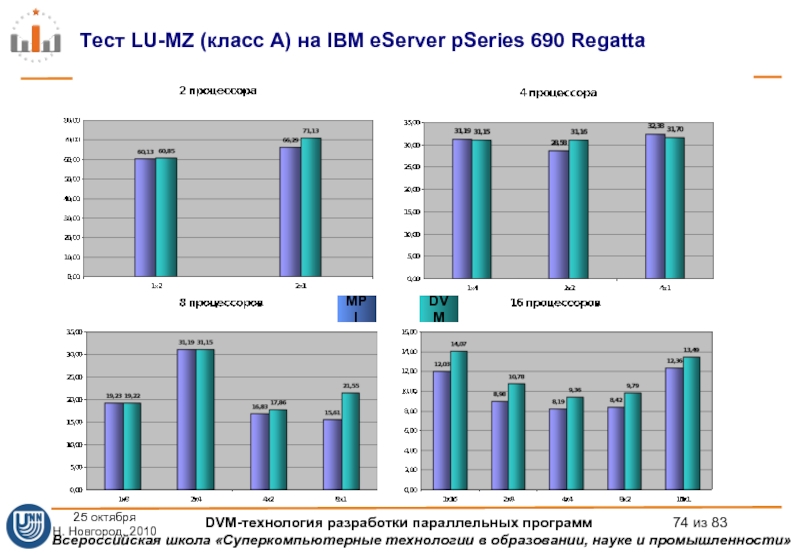
Слайд 74Тест LU-MZ (класс A) на IBM eServer pSeries 690 Regatta

DVM
MPI
25 октября
Н.

Новгород, 2010

DVM-технология разработки параллельных программ из 83

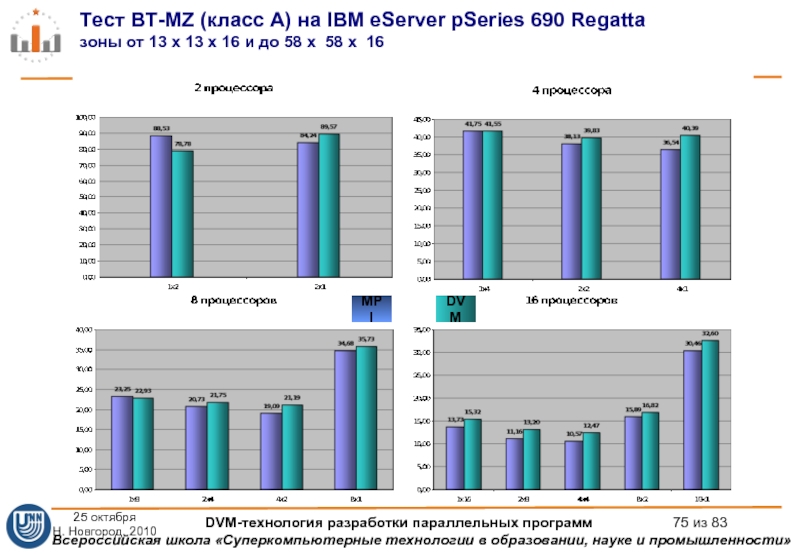
Слайд 75Тест BT-MZ (класс A) на IBM eServer pSeries 690 Regatta зоны от

13 x 13 x 16 и до 58 x 58 x 16


DVM

MPI

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 76
Ликвидация или сокращение дублирования данных в памяти узла.
Дополнительный уровень параллелизма на

OpenMP реализовать проще, чем на MPI (например, когда в программе есть два уровня параллелизма – параллелизм между подзадачами и параллелизм внутри подзадачи).
Улучшение балансировки на многоблочных задачах при меньшей трудоемкости реализации еще одного уровня параллелизма.

Преимущества гибридной модели MPI/OpenMP

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 77
Близость моделей OpenMP и DVM, что упрощает их совместное использование.
Получение гибких

программ, способных настраиваться на неоднородность узлов SMP-кластера.
Возможность использования параллельной программы как последовательной, как OpenMP-программы, как DVM-программы, и как DVM/OpenMP -программы.

Преимущества гибридной модели DVM/OpenMP

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 78
Гибридная вычислительная система – это параллельная вычислительная система, в которой, наряду

с универсальными процессорами, используются различные типы ускорителей, или сопроцессоров, обладающих нестандартной архитектурой (векторной, мультитредовой, реконфигурируемой под конкретную задачу и т. п.).

В идеале должна снабжаться также нестандартной, усиленной системой межузловых коммуникаций.

Гибридные вычислительные системы

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

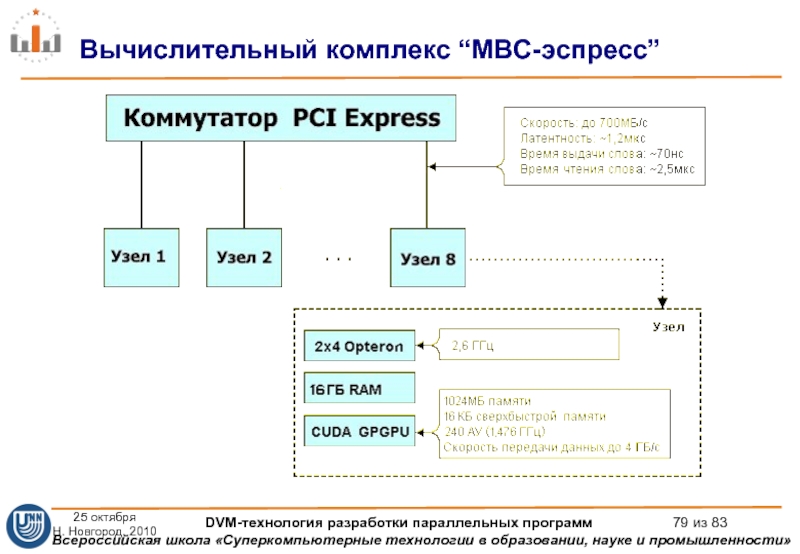
Слайд 79
Вычислительный комплекс “МВС-эспресс”
25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных

программ из 83

Слайд 80
!$acc data region copy(a(1:n,1:m)) local(b(2:n-1,2:m-1)) copyin(w(2:n-1))
do while(resid .gt. tol)

resid = 0.0
!$acc region
do i = 2, n-1
do j = 2, m-1
b(i,j) = 0.25*w(i)*(a(i-1,j)+a(i,j-1)+ &
a(i+1,j)+a(i,j+1)) &
+(1.0-w(i))*a(i,j)
enddo
enddo

Модель PGI Accelerator для Fortran и Си

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 81
do i = 2, n-1

do j = 2, m-1
resid = resid + (b(i,j)-a(i,j))**2
a(i,j) = b(i,j)
enddo
enddo
!$acc end region
enddo
!$acc end data region

http://www.pgroup.com/lit/whitepapers/pgi_accel_prog_model_1.2.pdf

Модель PGI Accelerator для Fortran и Си

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 82
OpenMP Application Program Interface Version 3.0, May 2008.
http://www.openmp.org/mp-documents/spec30.pdf
MPI: A

Message-Passing Interface Standard Version 2.2, September 2009. http://www.mpi-forum.org/docs/mpi-2.2/mpi22-report.pdf
Параллельное программирование на языке C-DVM. Методическое пособие по практикуму для студентов 2-4 курсов. МГУ им. М.В.Ломоносова. Факультет ВMиК. Москва, 2002 г. ftp://ftp.keldysh.ru/K_student/DVM-practicum/method_CDVM_2006.doc
Антонов А.С. Параллельное программирование с использованием технологии OpenMP: Учебное пособие.-М.: Изд-во МГУ, 2009.
http://parallel.ru/info/parallel/openmp/OpenMP.pdf
Антонов А.С. Параллельное программирование с использованием технологии MPI: Учебное пособие.-М.: Изд-во МГУ, 2004.
http://parallel.ru/tech/tech_dev/MPI/mpibook.pdf
Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002.

Литература

25 октября
Н. Новгород, 2010

DVM-технология разработки параллельных программ из 83

Слайд 83

Вопросы?
25 октября
Н. Новгород, 2010
DVM-технология разработки параллельных программ

из 83

Похожие презентации

Модернизация среднего профессионального образования 318
Биография и жизнь Григория Белых 318
Эльдар Александрович Рязанов. Рожденный быть режиссером 632
Информационные системы 236
Дмитрий Иванович Менделеев – орыс химигі 413
в школе 244

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика