- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
A презентация
Содержание
- 1. A
- 2. Abstract maths… for us? Dizzyingly abstract branch
- 3. The plan Basic Category Theory concepts New
- 4. A bit of background 1940s Eilenberg, Mac
- 5. I. Categories
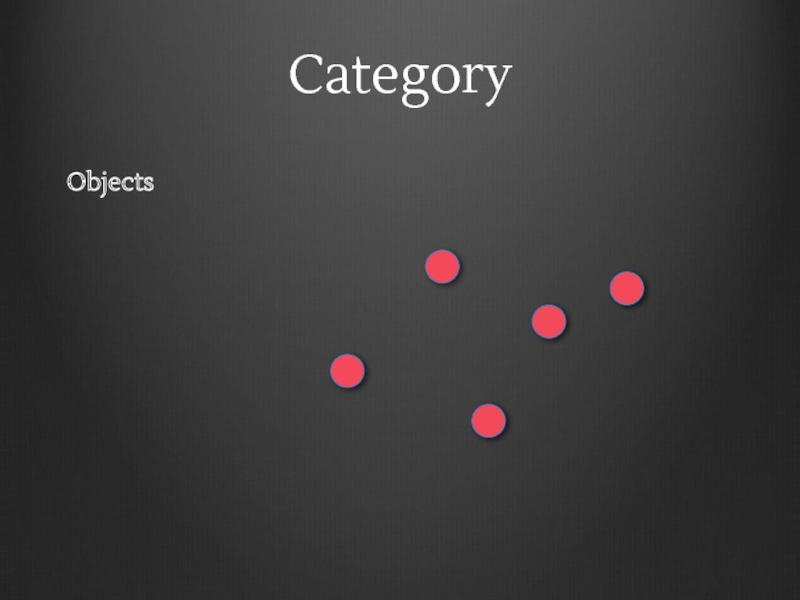
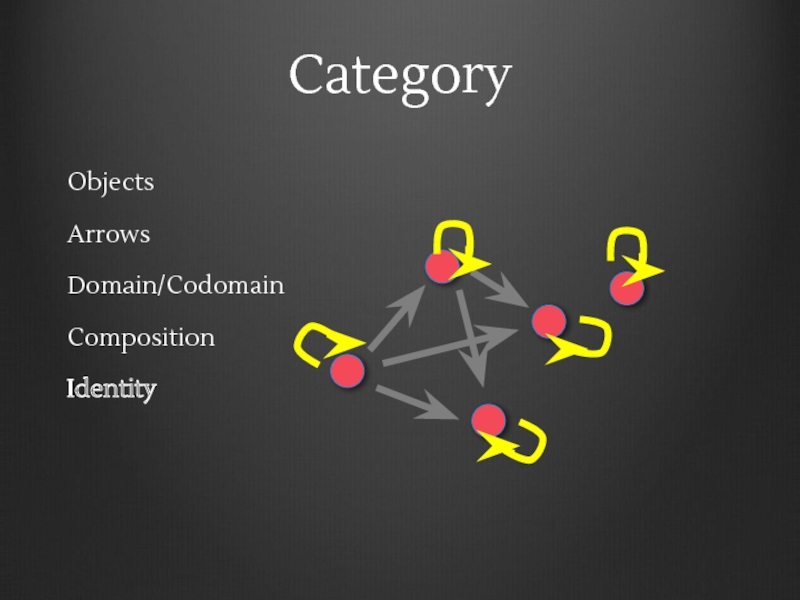
- 6. Category Objects
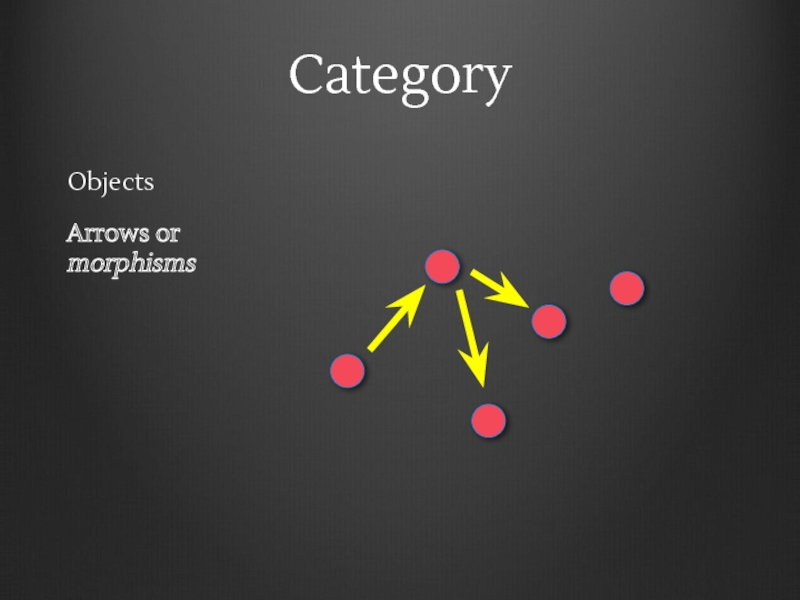
- 7. Category Objects Arrows or morphisms
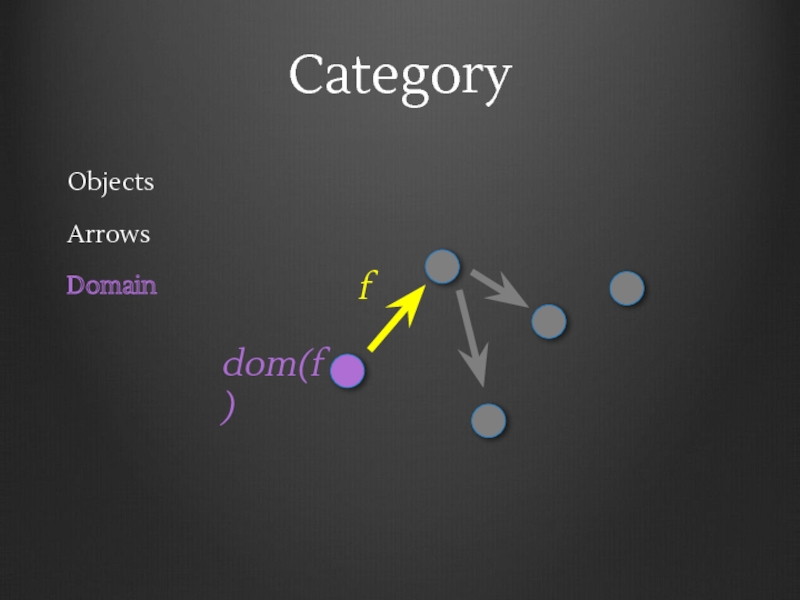
- 8. Category Objects Arrows Domain f dom(f)
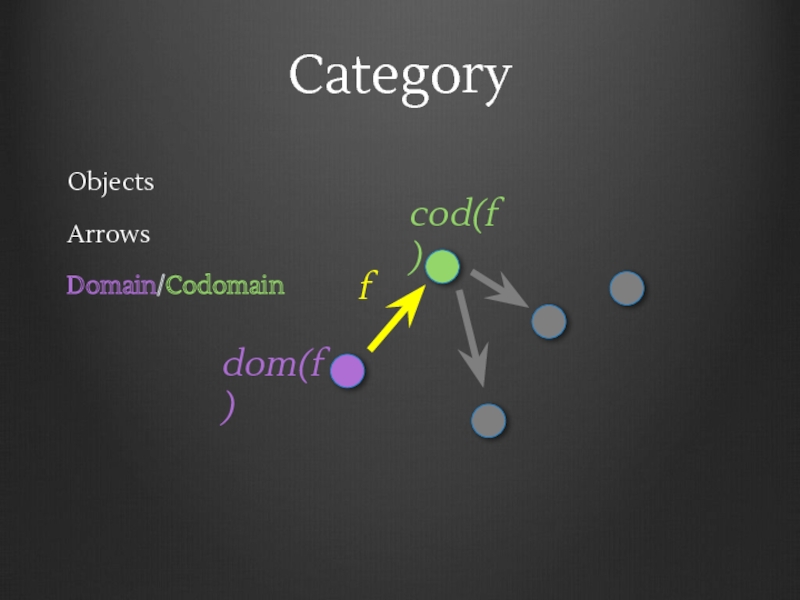
- 9. Category Objects Arrows Domain/Codomain f cod(f) dom(f)
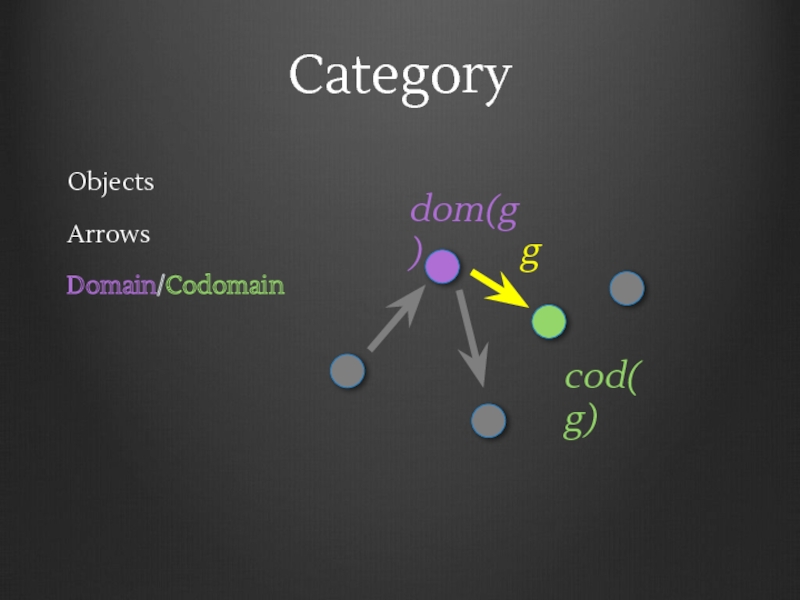
- 10. Category Objects Arrows Domain/Codomain dom(g) cod(g) g
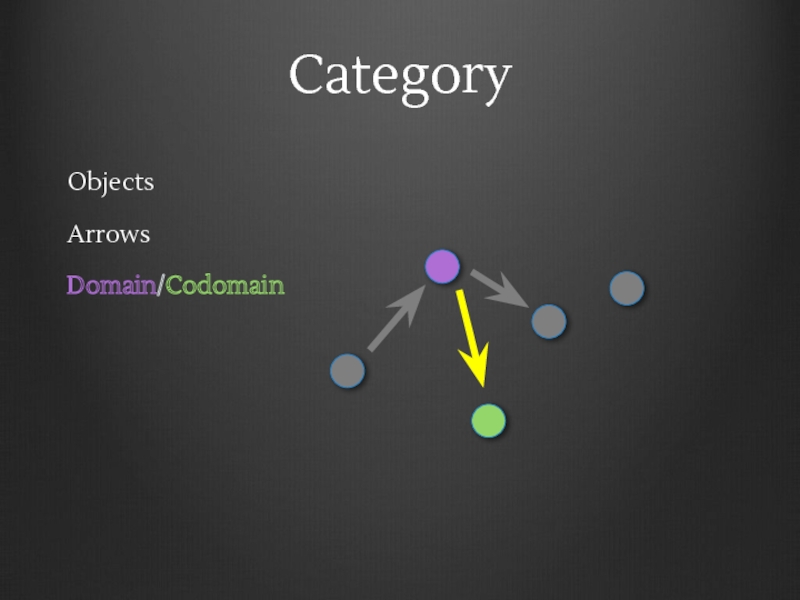
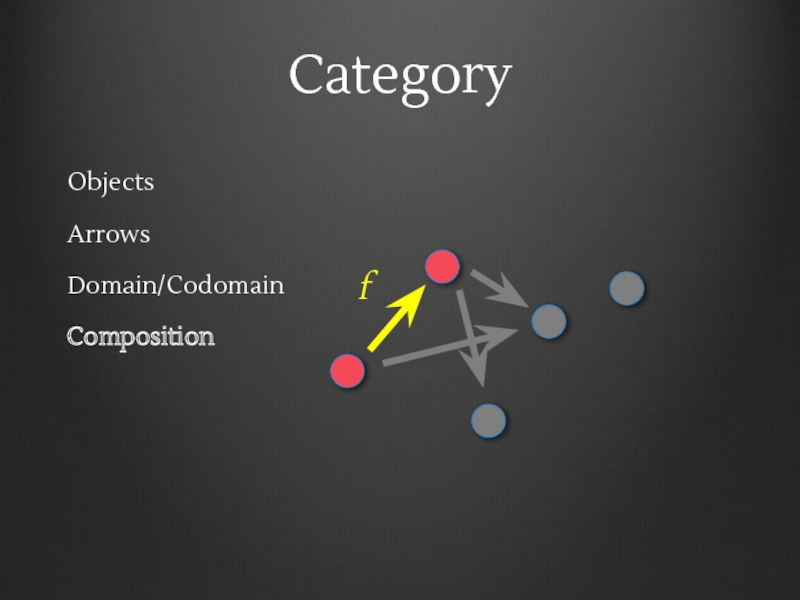
- 11. Category Objects Arrows Domain/Codomain
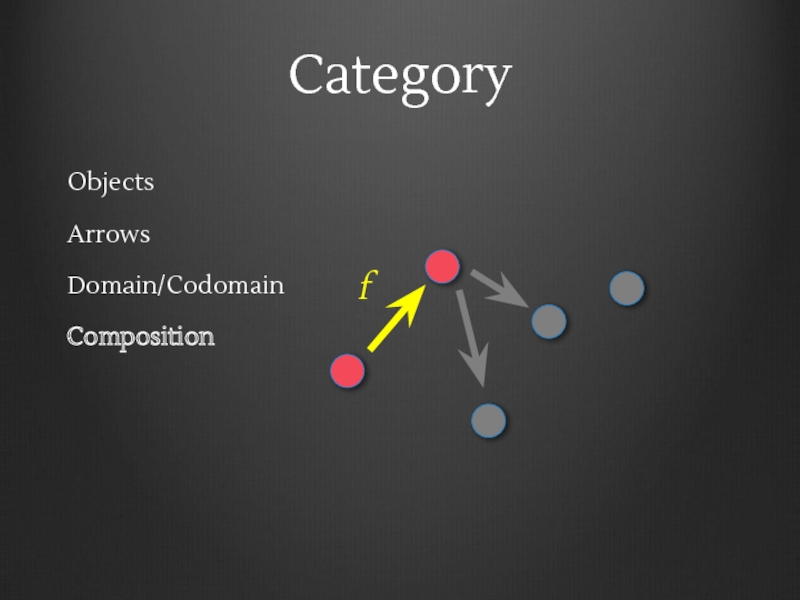
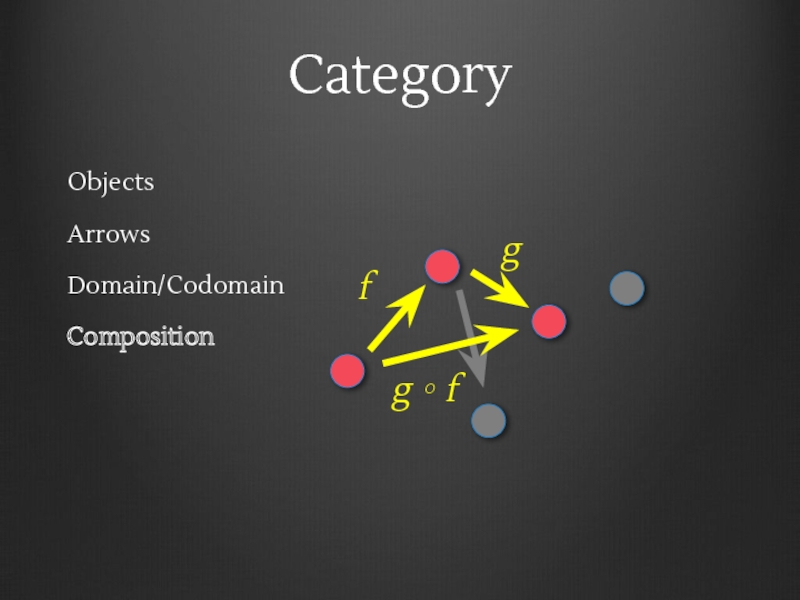
- 12. Category Objects Arrows Domain/Codomain Composition f
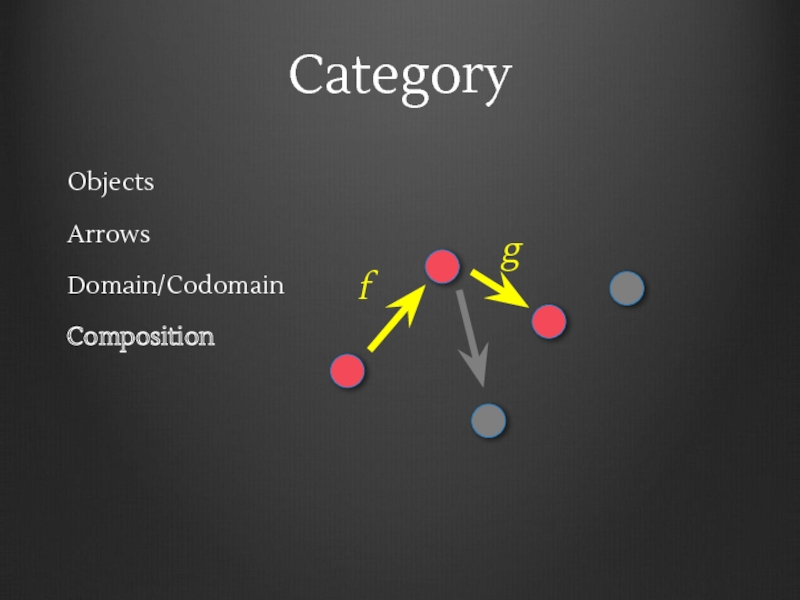
- 13. Category Objects Arrows Domain/Codomain Composition f g
- 14. Category Objects Arrows Domain/Codomain Composition f g g ∘ f
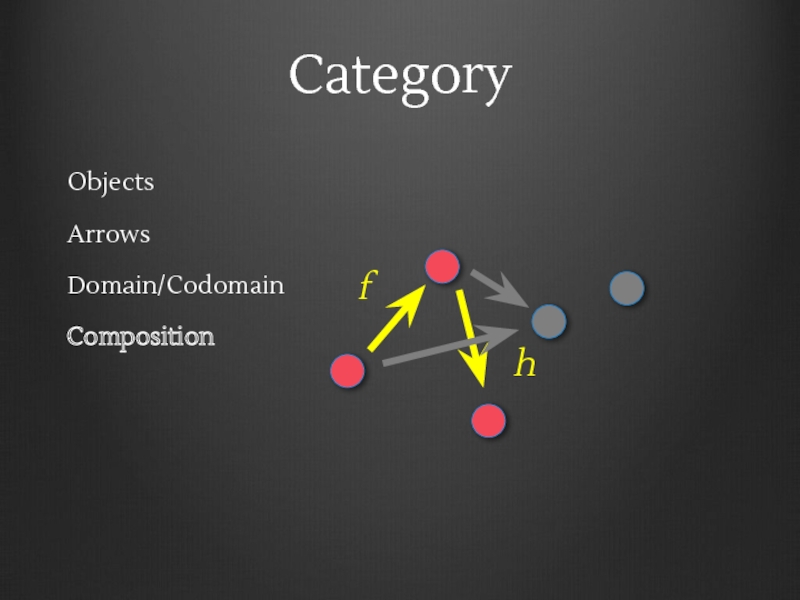
- 15. Category Objects Arrows Domain/Codomain Composition f
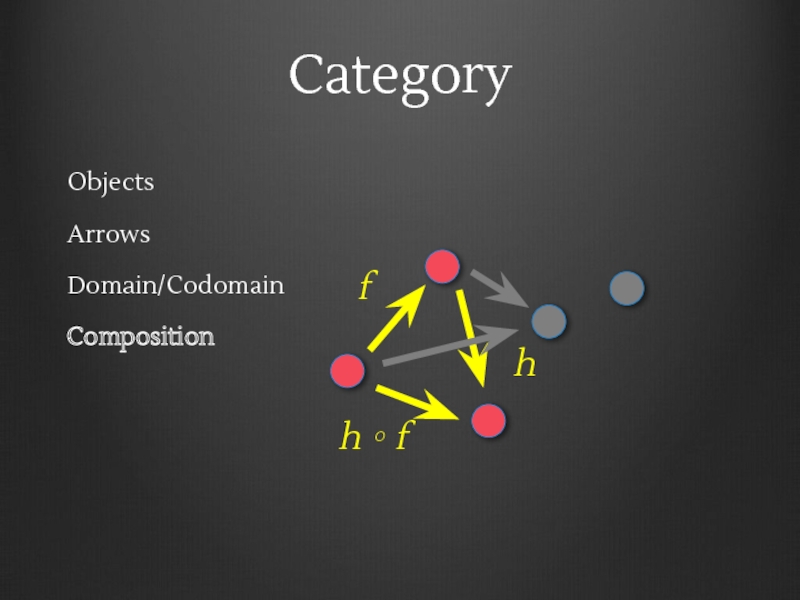
- 16. Category Objects Arrows Domain/Codomain Composition f h
- 17. Category Objects Arrows Domain/Codomain Composition f h h ∘ f
- 18. Category Objects Arrows Domain/Codomain Composition Identity
- 19. Category Compose ∘ : (B ? C)
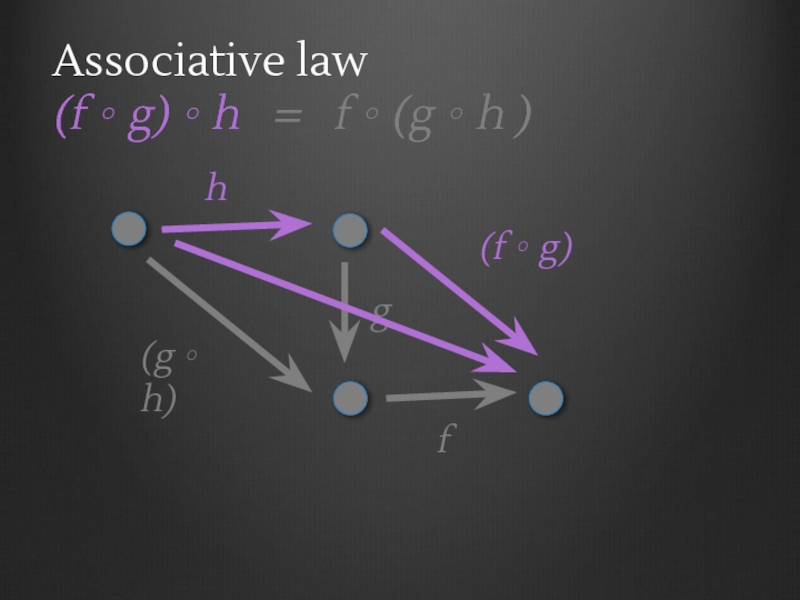
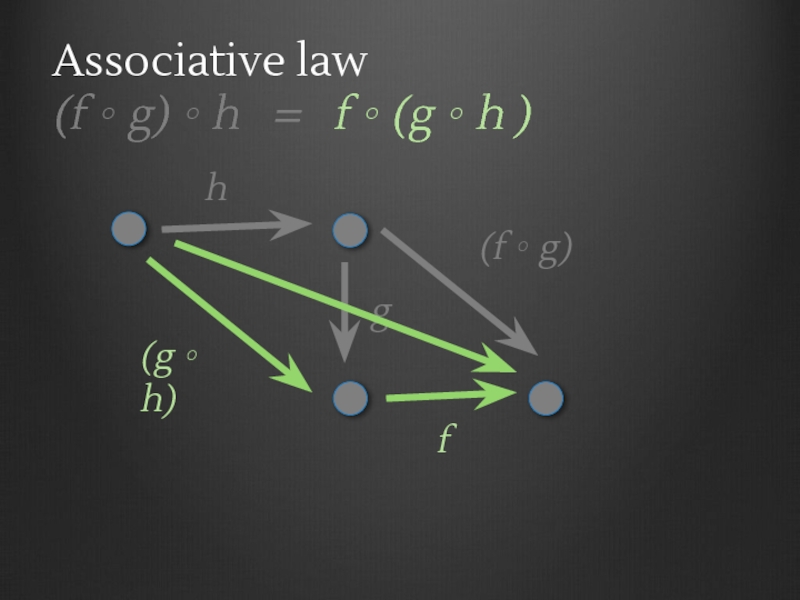
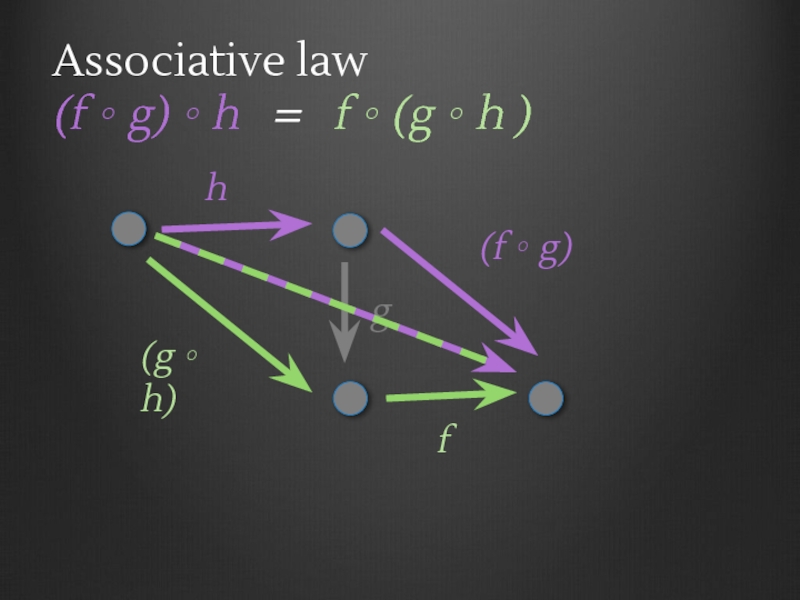
- 20. Category Laws Associative Law (f ∘ g)
- 21. Associative law (f ∘ g)
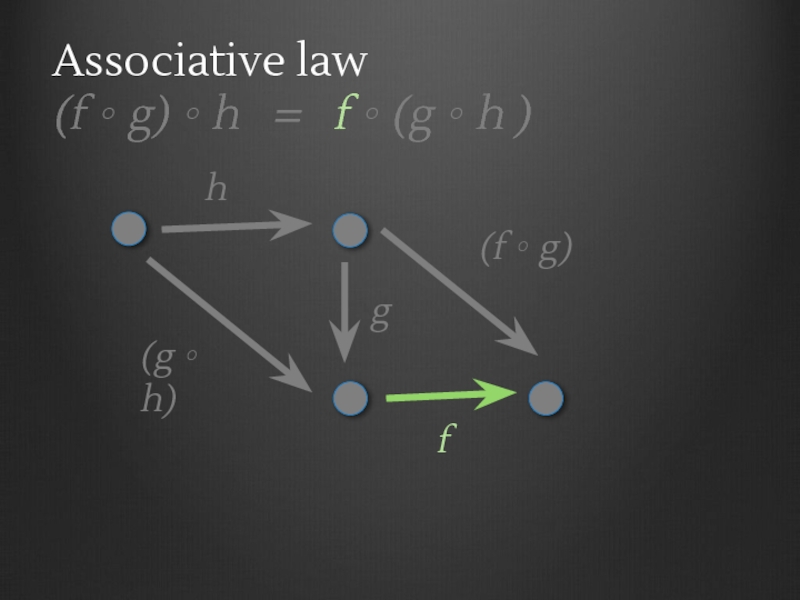
- 22. Associative law (f ∘ g)
- 23. Associative law (f ∘ g)
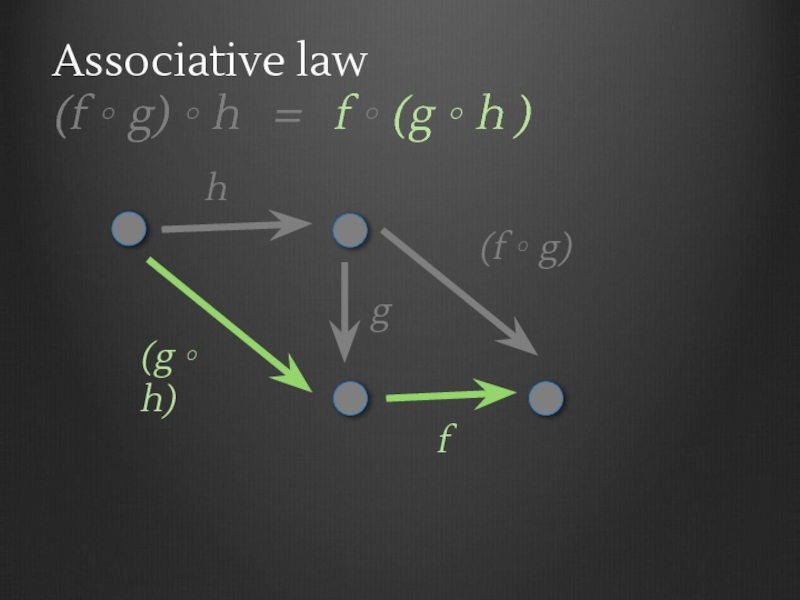
- 24. Associative law (f ∘ g)
- 25. Associative law (f ∘ g)
- 26. Associative law (f ∘ g)
- 27. Associative law (f ∘ g)
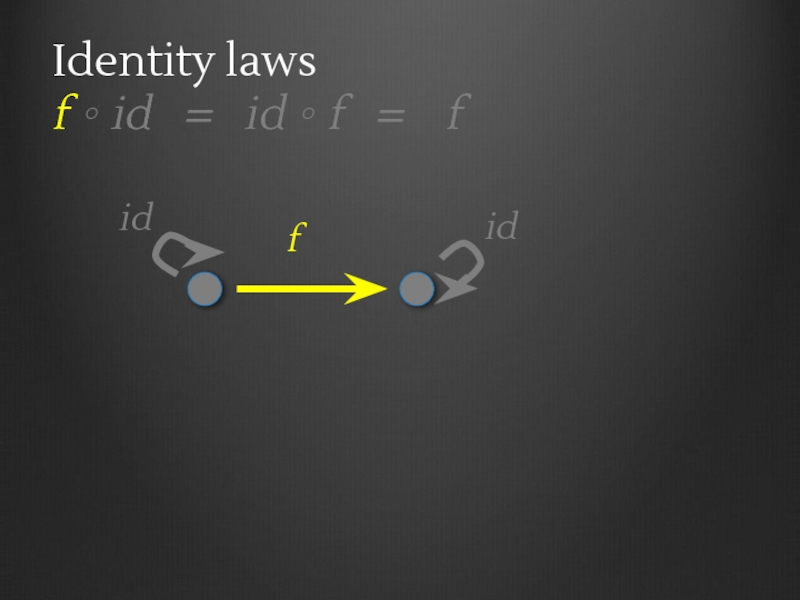
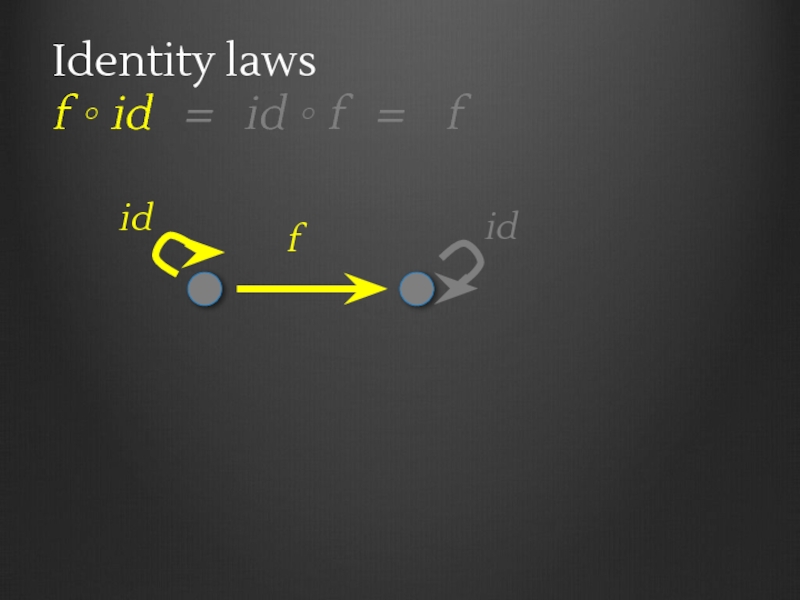
- 28. Identity laws f ∘ id
- 29. Identity laws f ∘ id
- 30. Identity laws f ∘ id
- 31. Identity laws f ∘ id
- 32. Examples Infinite categories Finite categories Objects can
- 33. Sets & functions Person String Integer bestFriend length name age +1
- 34. Sets & functions Infinite arrows from composition
- 35. Sets & functions Objects Arrows Composition Identity
- 36. Sets & functions Objects = sets (or
- 37. Zero
- 38. One
- 39. Two
- 40. Three
- 41. Class hierarchy IFruit IBanana AbstractBanana BananaImpl MockBanana Tool Spanner
- 42. Class hierarchy Objects Arrows Composition Identity
- 43. Class hierarchy Objects = classes Arrows =
- 44. Class hierarchy Partially ordered sets (posets)
- 45. World Wide Web www.naaawcats.com No dogs
- 46. World Wide Web Objects = webpages Arrows = hyperlinks Composition = Links don’t compose Identity
- 47. World Wide Web Graphs Objects =
- 48. “Free Category” from graphs! Objects = nodes
- 49. Categories in code trait Category[Arrow[_,_]] {
- 50. Category of Types & Functions object FnCat
- 51. Category of Garden Hoses sealed trait Hose[In,
- 52. Category of Garden Hoses [live code example]
- 53. Categories embody the principle of strongly-typed composability
- 54. II. Functors
- 55. Functors Functors map between categories Objects ? objects Arrows ? arrows Preserves composition & identity
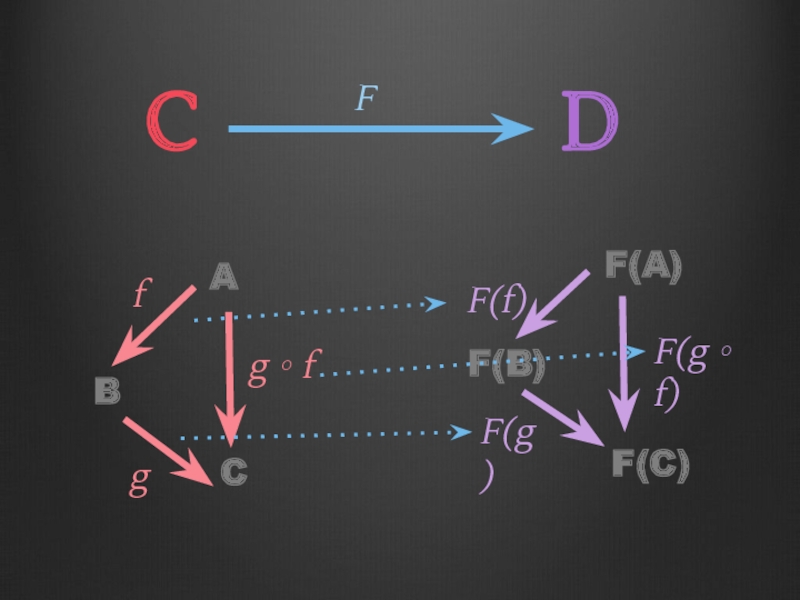
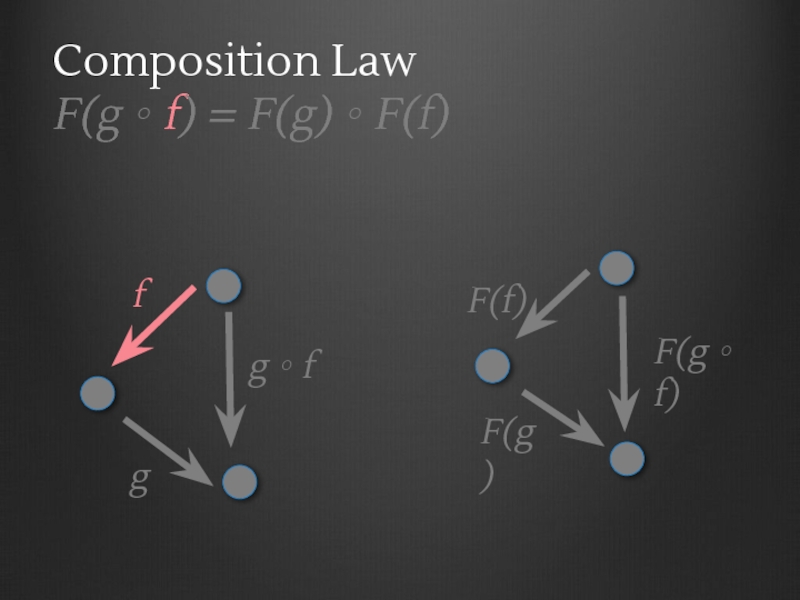
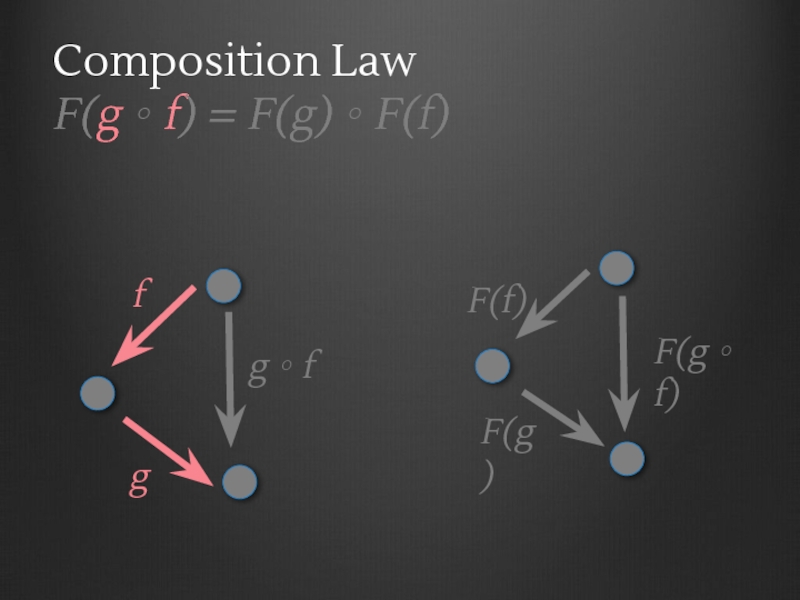
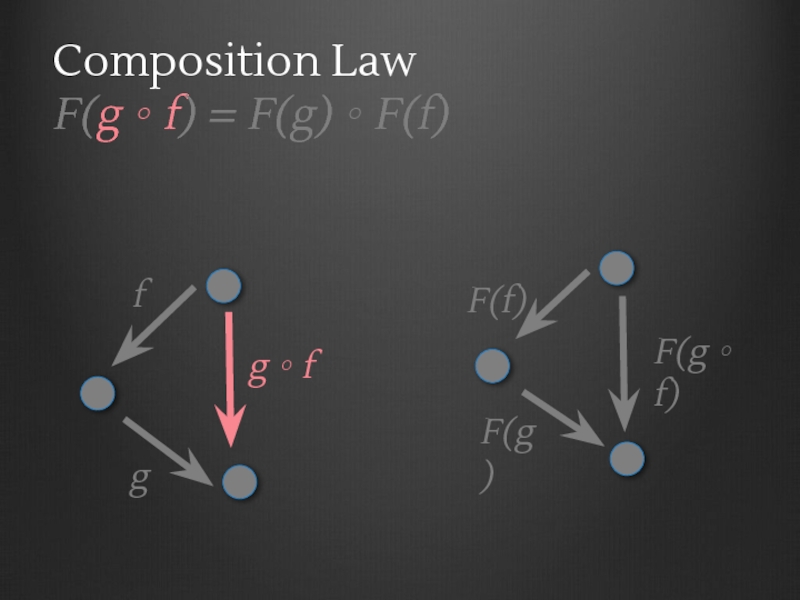
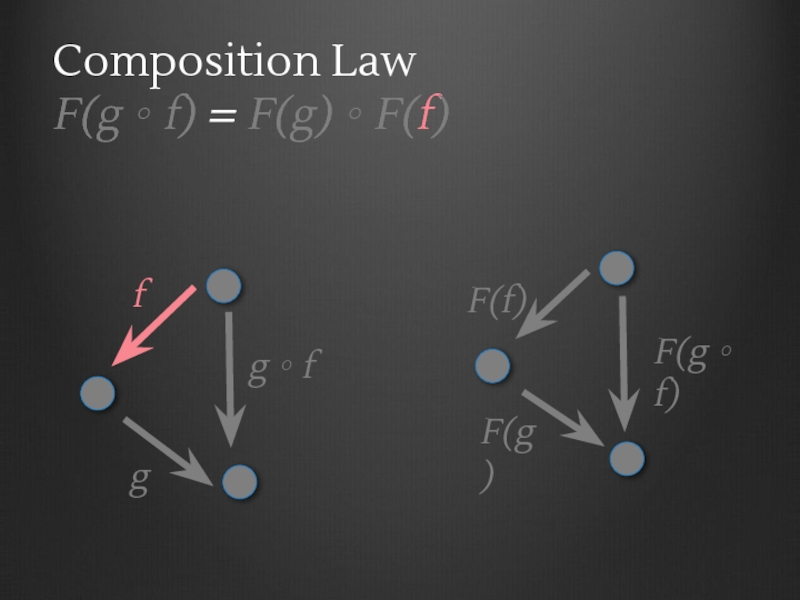
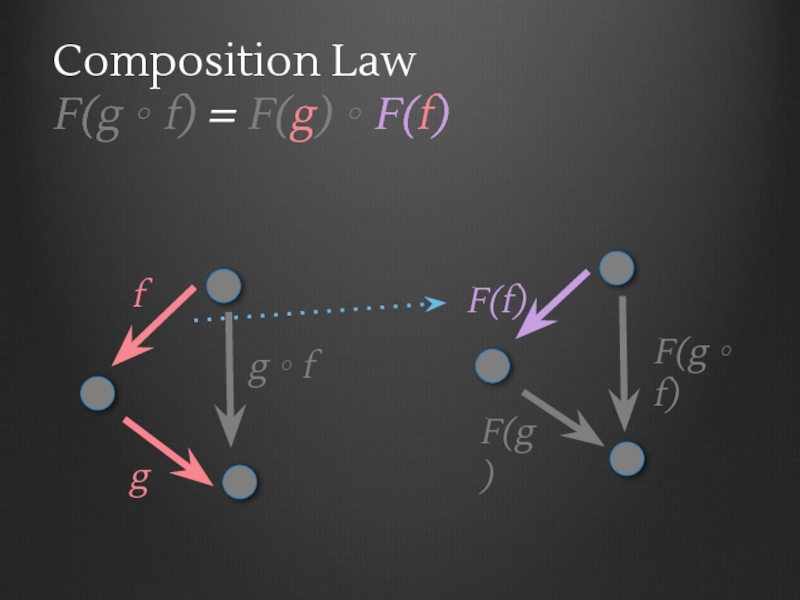
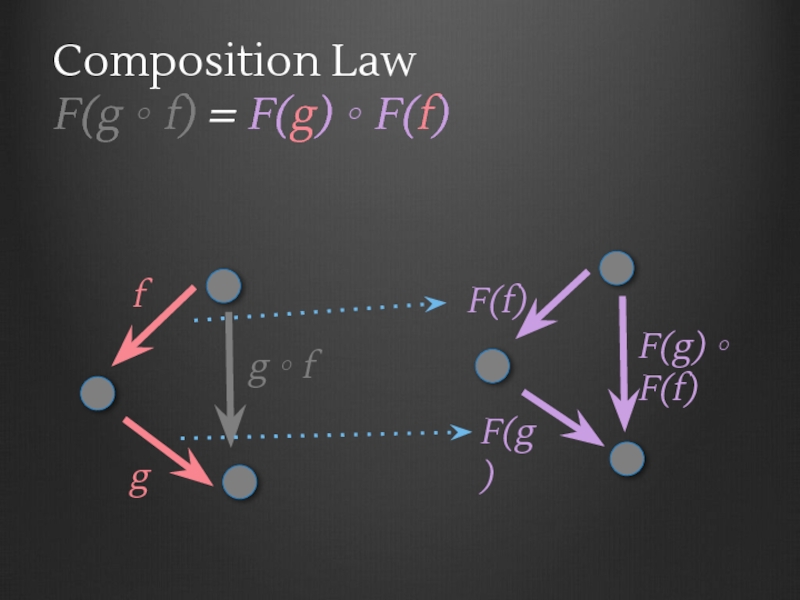
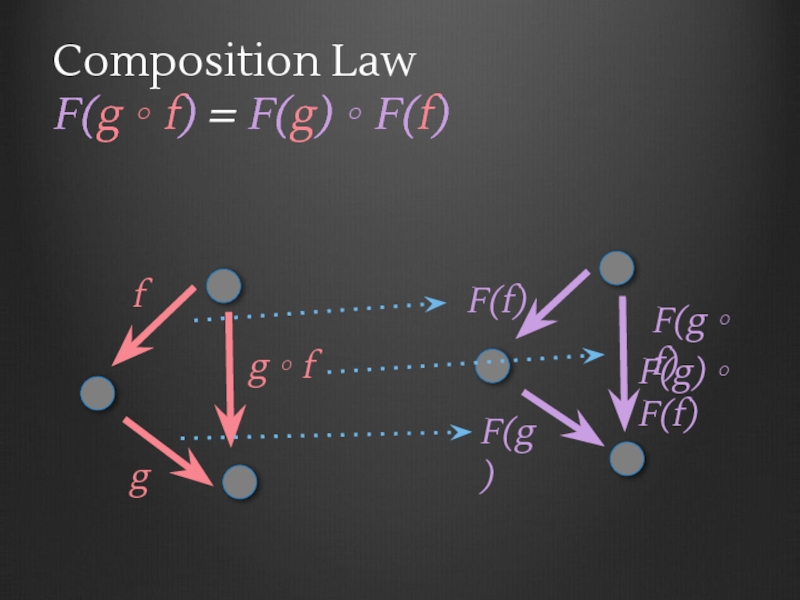
- 56. Functor laws Composition Law F(g ∘ f)
- 57. C F D Category Category Functor
- 58. C F D Category Category Functor Cat Category of categories
- 59. C F D Category Category Functor Cat
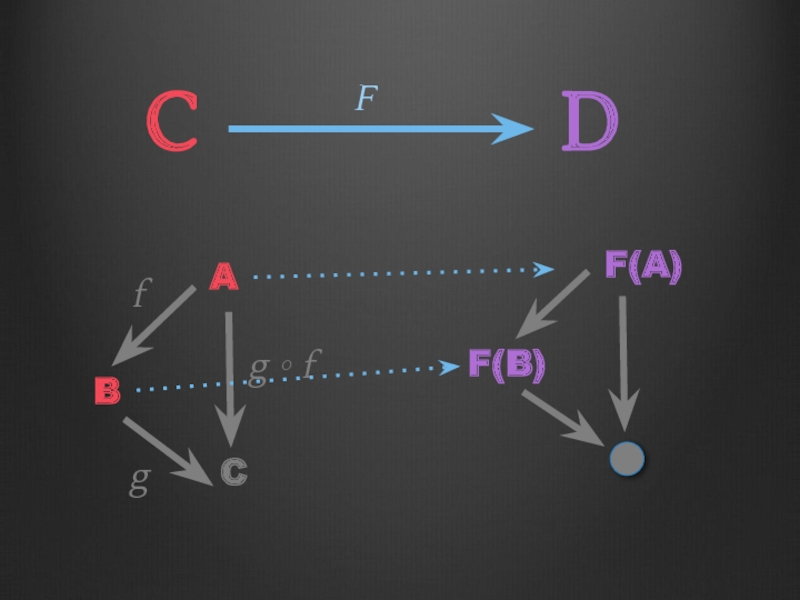
- 60. C F D A B C g ∘ f f g
- 61. C F D A B C g ∘ f f g F(A)
- 62. C F D A B C g ∘ f f g F(A) F(B)
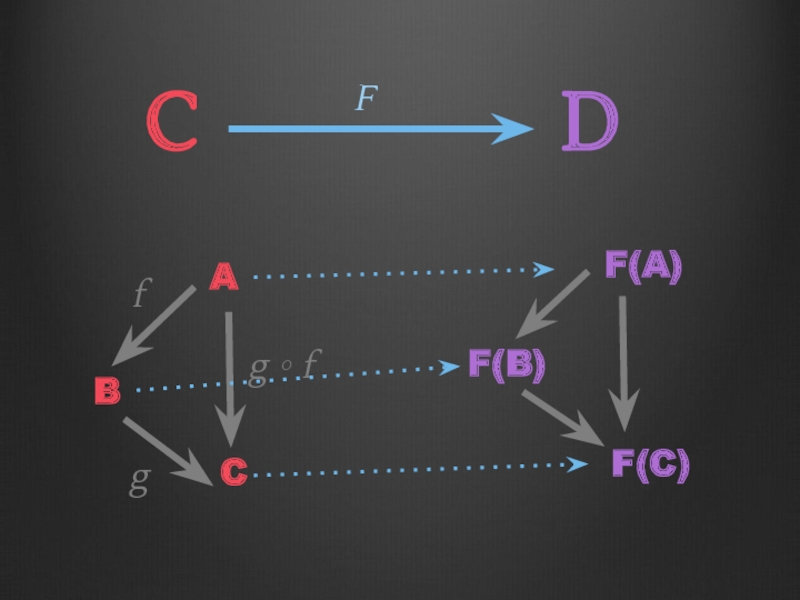
- 63. C F D A B C g ∘ f f g F(A) F(B) F(C)
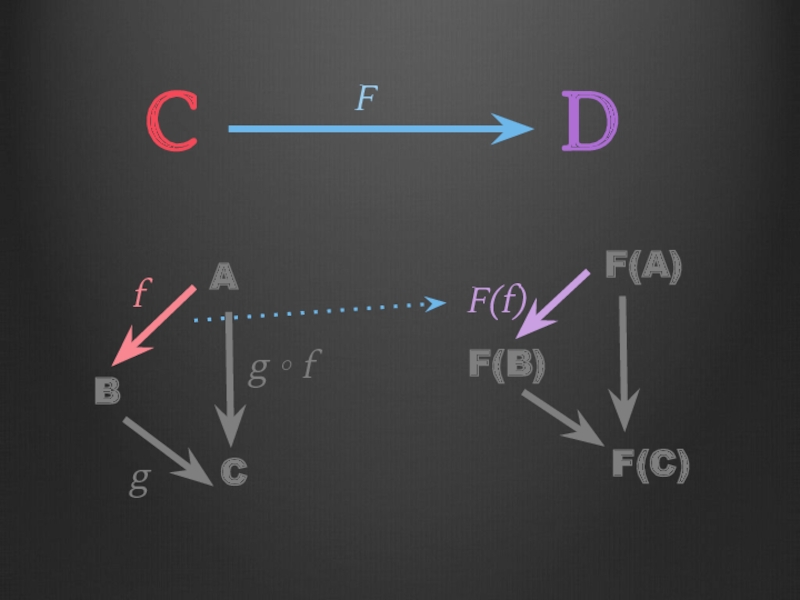
- 64. C F D A B C g ∘ f f g F(A) F(B) F(C) F(f)
- 65. C F D A B C g
- 66. C F D A B C g
- 67. g ∘ f f g F(f) F(g)
- 68. g ∘ f f g F(f) F(g)
- 69. g ∘ f f g F(f) F(g)
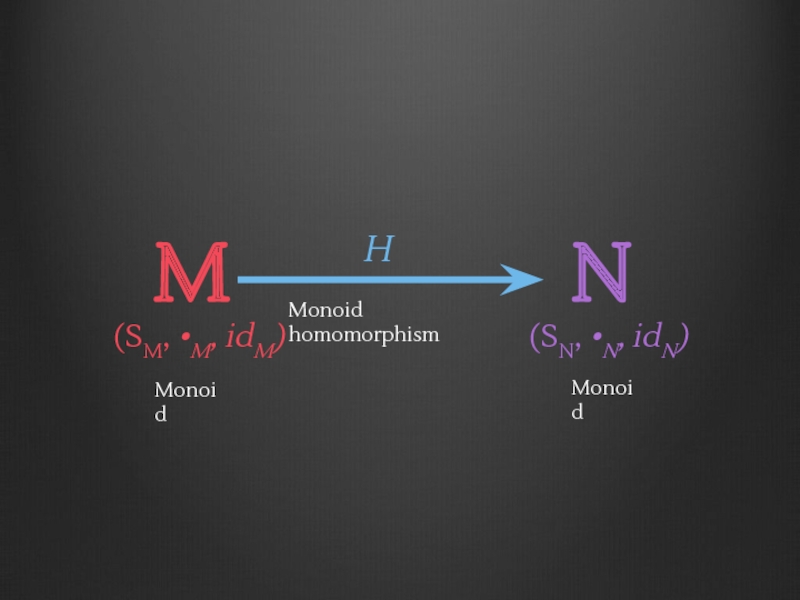
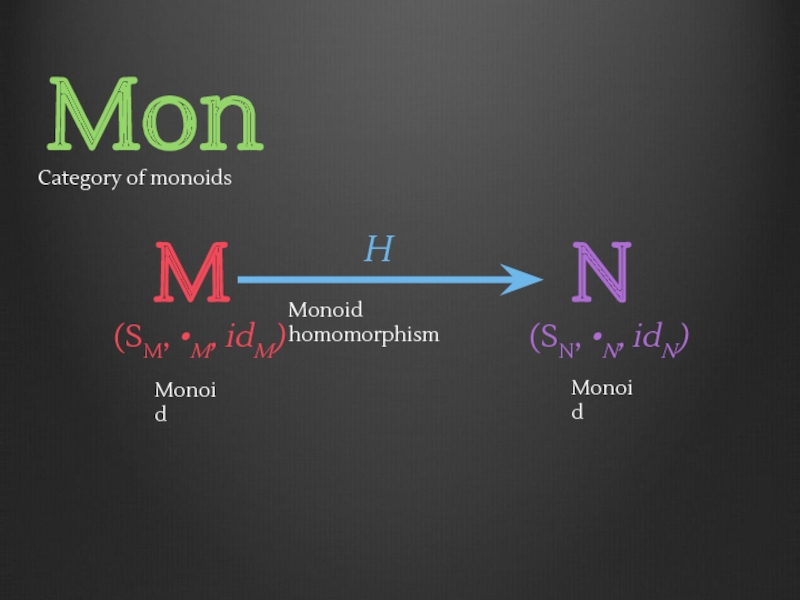
- 70. g ∘ f f g F(f) F(g)
- 71. g ∘ f f g F(f) F(g)
- 72. g ∘ f f g F(f) F(g)
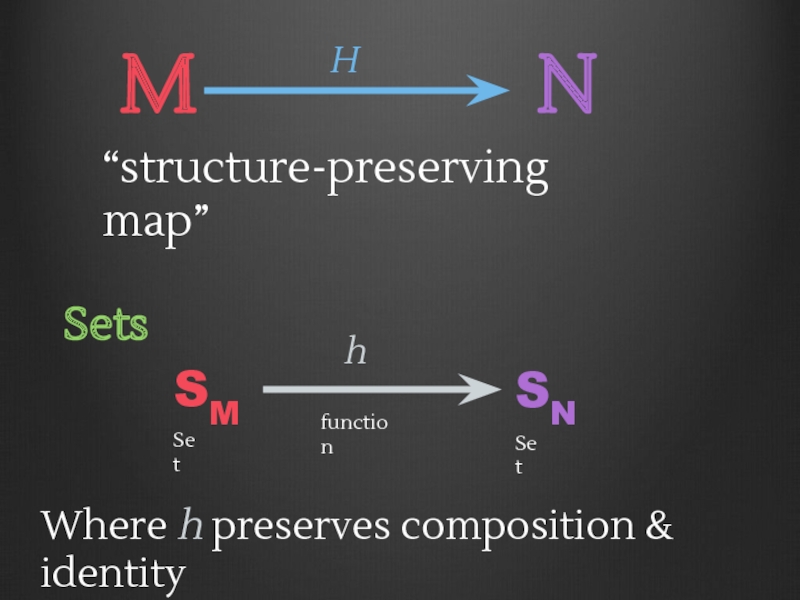
- 73. g ∘ f f g F(f) F(g)
- 74. g ∘ f f g F(f) F(g)
- 75. g ∘ f f g F(f) F(g)
- 76. g ∘ f f g F(f) F(g)
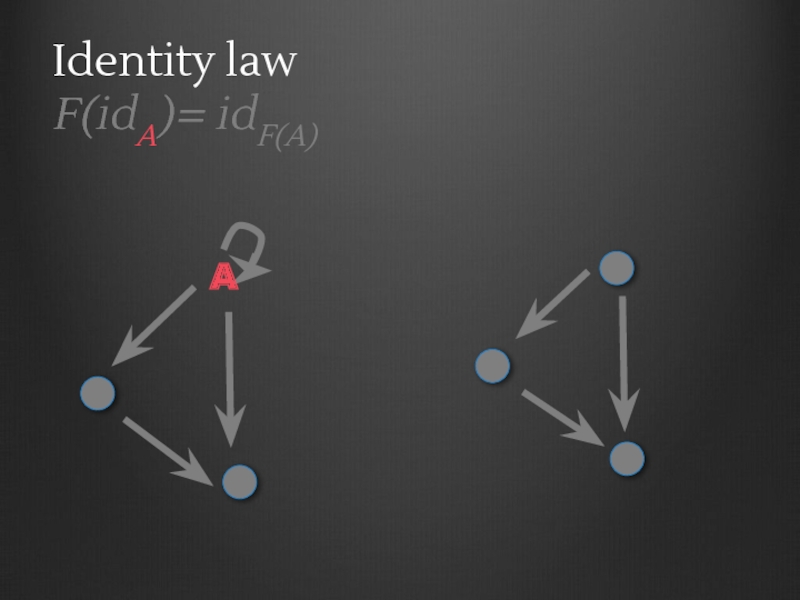
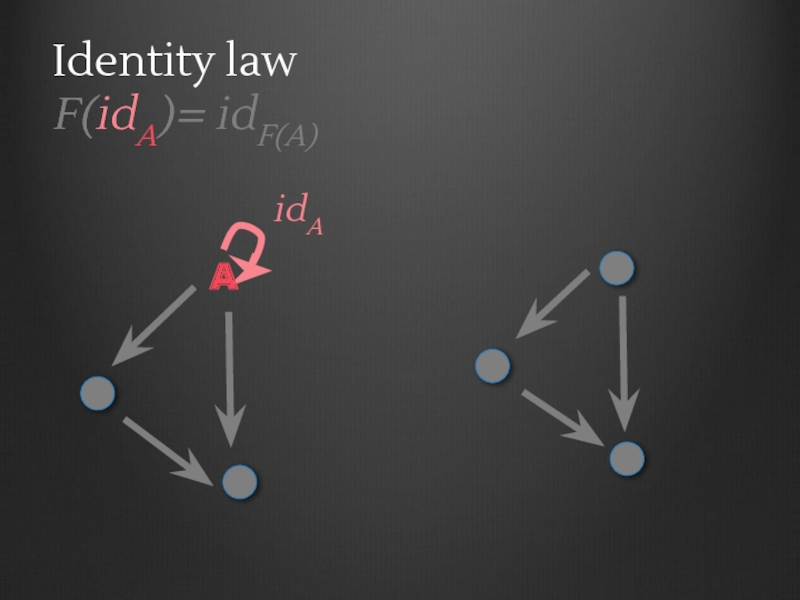
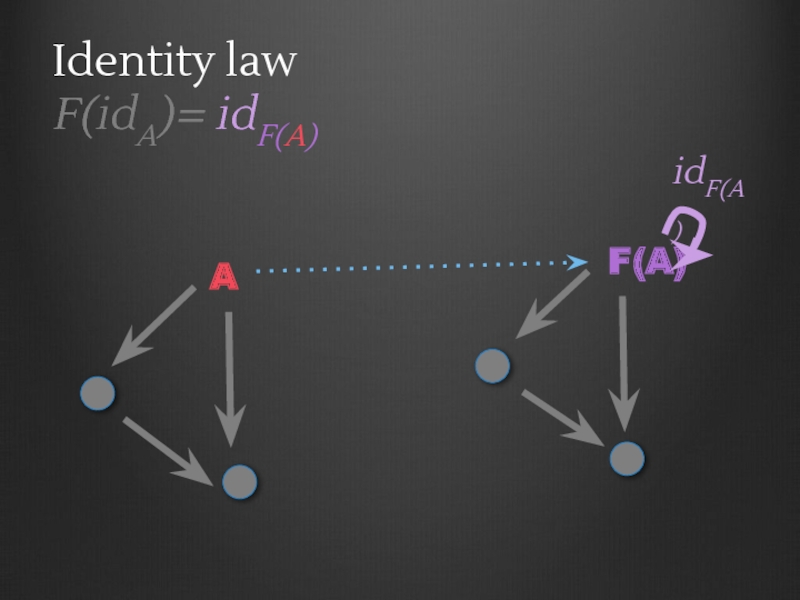
- 77. Identity law F(idA)= idF(A) A
- 78. Identity law F(idA)= idF(A) A idA
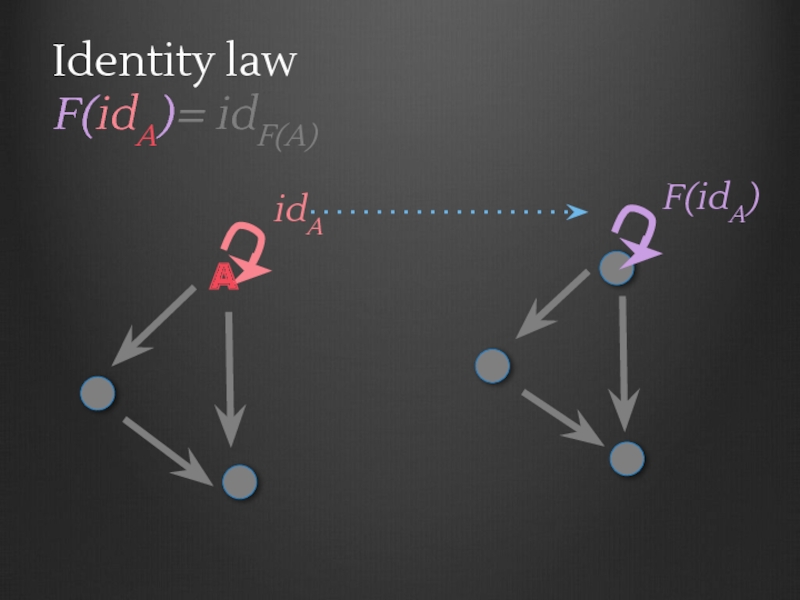
- 79. Identity law F(idA)= idF(A) A idA F(idA)
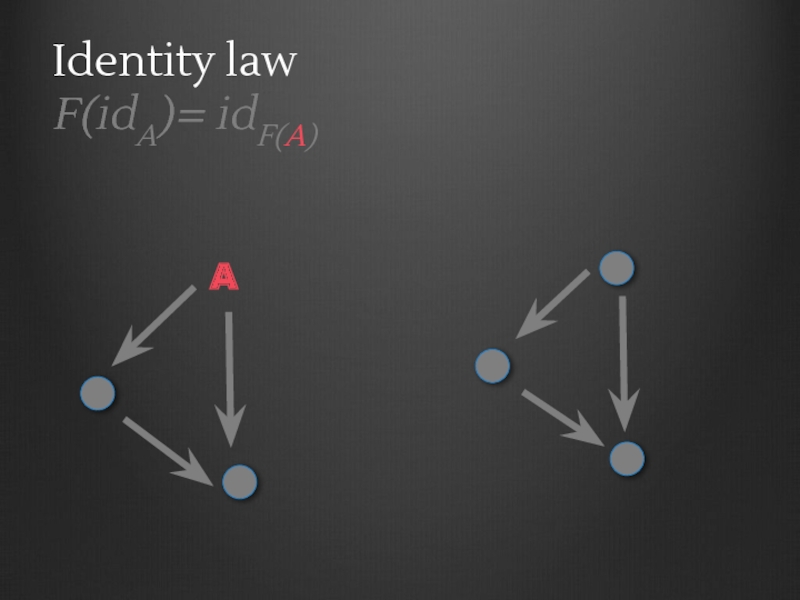
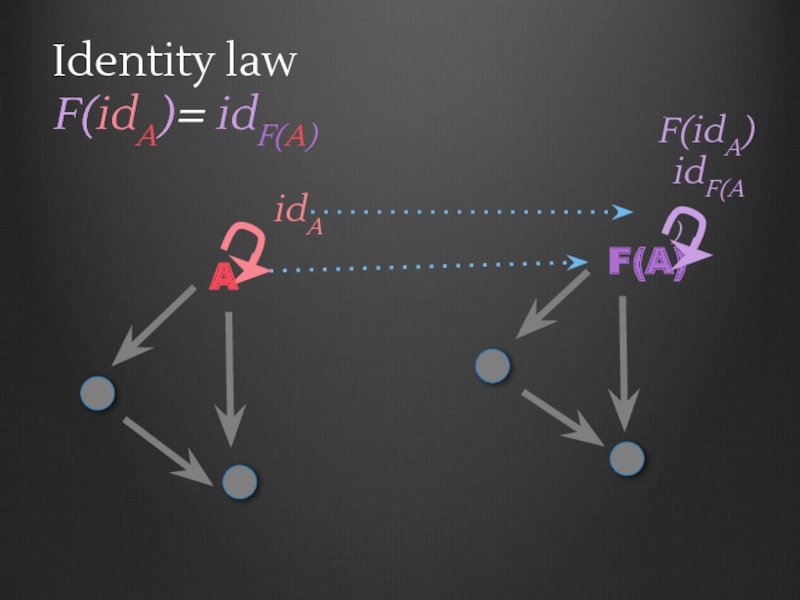
- 80. Identity law F(idA)= idF(A) A
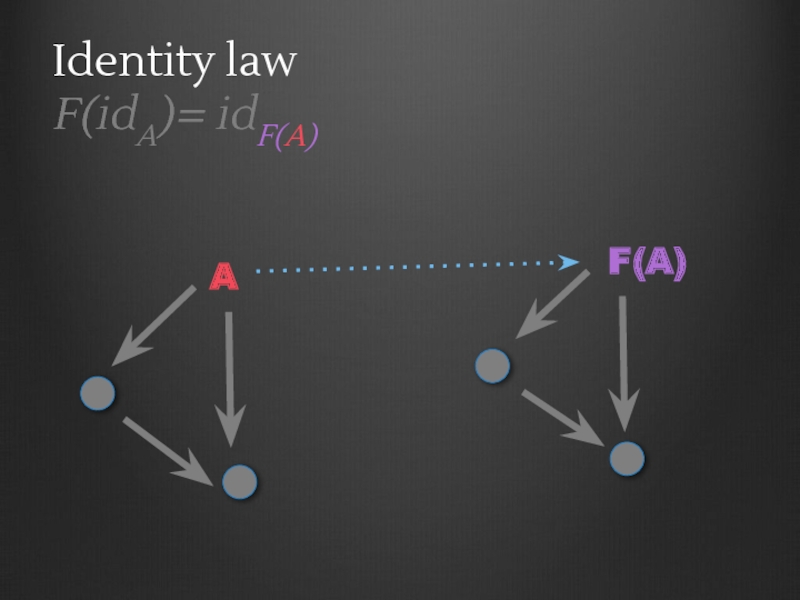
- 81. Identity law F(idA)= idF(A) A F(A)
- 82. Identity law F(idA)= idF(A) A F(A) idF(A)
- 83. Identity law F(idA)= idF(A)
- 84. Terminology homomorphism
- 85. Terminology homomorphism Same
- 86. Terminology homomorphism Same -shape-ism
- 87. Terminology homomorphism “structure preserving map”
- 88. Terminology homomorphism Functors are “category homomorphisms”
- 89. Functors in code trait Functor[F[_]] {
- 90. Functors in code trait Functor[F[_]] {
- 91. Functors in code trait Functor[F[_]] {
- 92. Functors in code trait Functor[F[_]] {
- 93. Functors laws in code fa.map(f).map(g) == fa.map(g compose f)
- 94. Functors laws in code fa.map(a => a) == fa
- 95. Terminology endomorphism
- 96. Terminology endomorphism Within
- 97. Terminology endomorphism Within -shape-ism
- 98. Terminology endomorphism “a mapping from something back to itself”
- 99. Terminology endo “a mapping from something back to itself”
- 100. Endofunctors In Scala, all our functors are
- 101. Endofunctors Luckily, we can represent any functor
- 102. List Functor sealed trait List[+A] case class
- 103. List Functor sealed trait List[+A] {
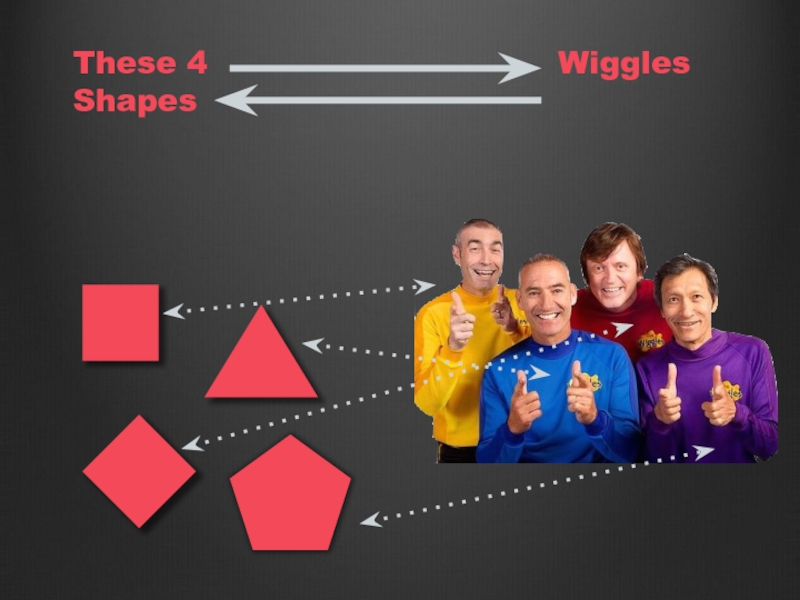
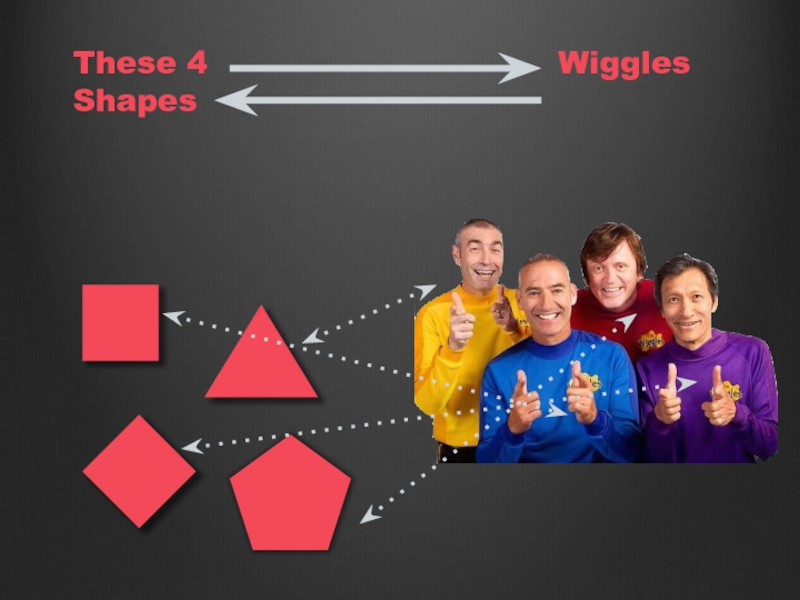
- 104. List Functor potatoList .map(mashEm) .map(boilEm) .map(stickEmInAStew)
- 105. List Functor userList .map(_.name) .map(_.length) .map(_ + 1) .map(_.toString)
- 106. Other functors trait Tree[A] trait Future[A] trait
- 107. Functors Fundamental concept in Category Theory Super
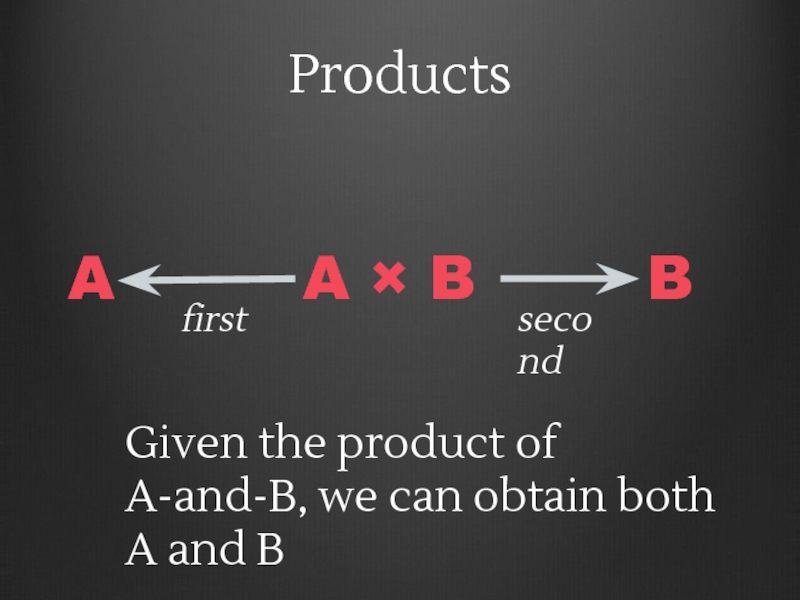
- 108. III. Monoids
- 109. Monoids Some set we’ll call M
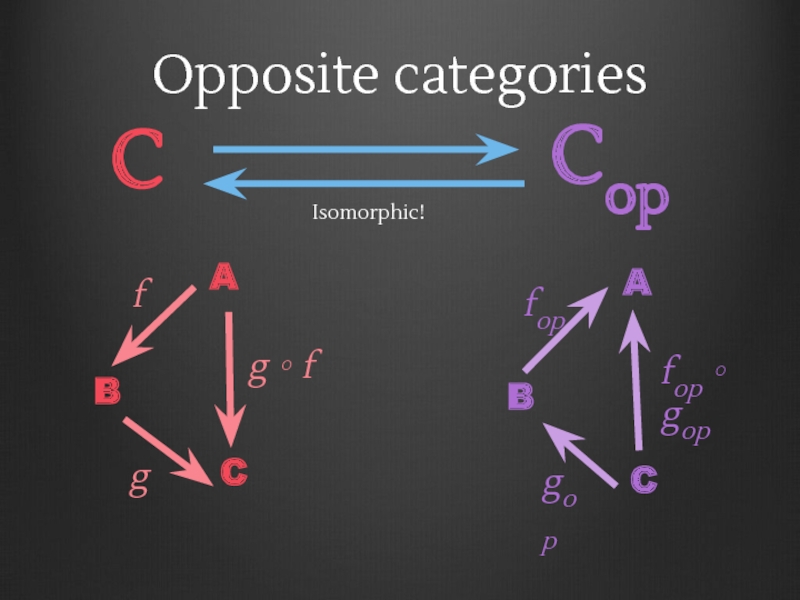
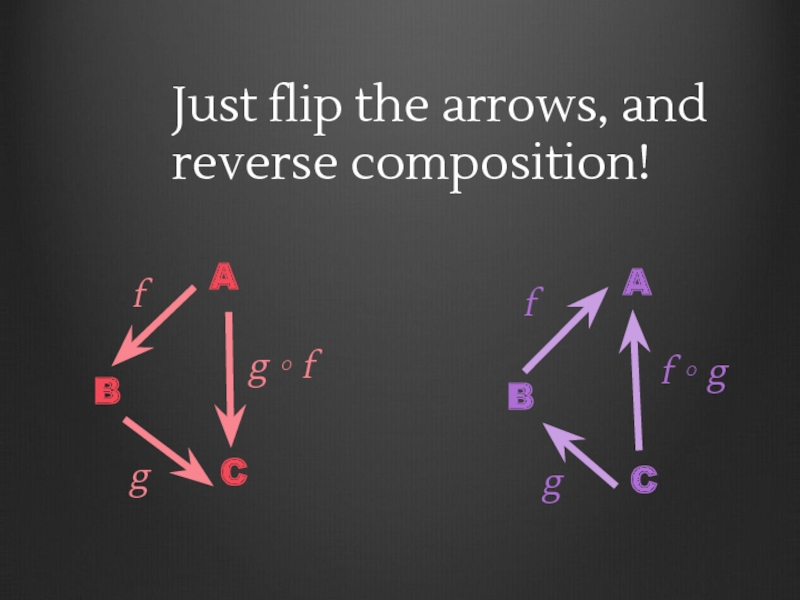
- 110. Monoid Laws Associative Law (f • g)
- 111. Category Laws Associative Law (f ∘ g)
- 112. Monoids Compose • : M
- 113. Category Compose ∘ : (B ? C)
- 114. Category with 1 object Compose ∘ :
- 115. Category with 1 object Compose ∘ :
- 116. Monoids are categories Each arrow is an
- 117. Monoids are categories Objects
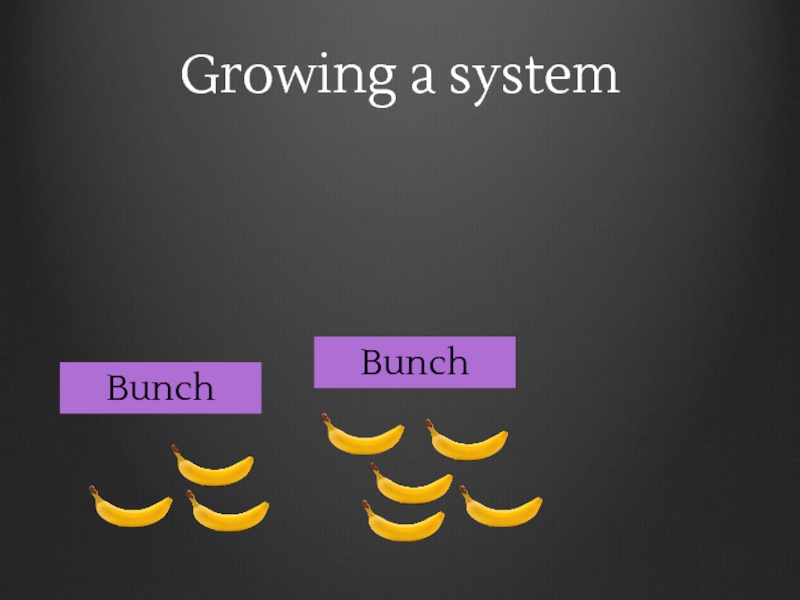
- 118. M H N Monoid Monoid Monoid homomorphism (SM, •M, idM) (SN, •N, idN)
- 119. M H N Monoid Monoid Monoid homomorphism
- 120. M H N Monoid Monoid Monoid homomorphism
- 121. M H N SM SN “structure-preserving map”
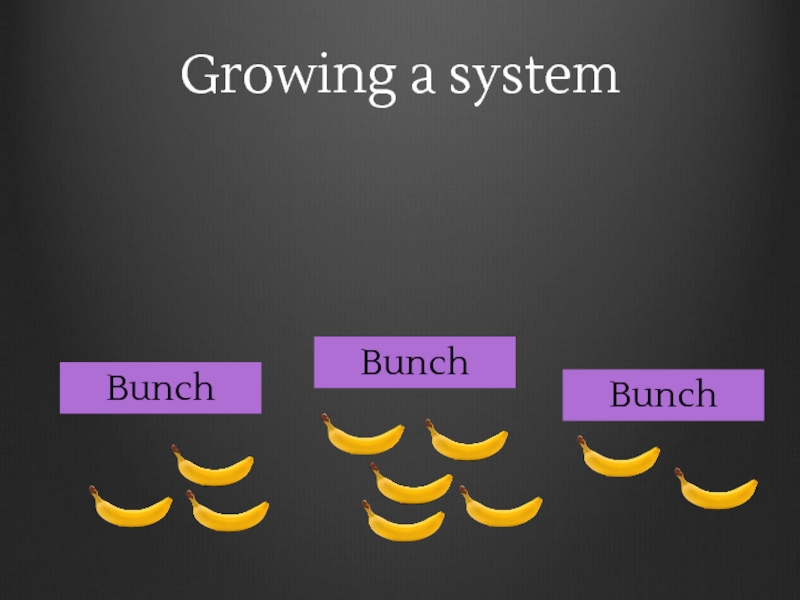
- 122. Example String length is a monoid homomorphism
- 123. Preserves identity Preserves composition "".length == 0
- 124. Monoids in code trait Monoid[M] {
- 125. Monoids in code def foldMonoid[M: Monoid](
- 126. Int / 0 / + import IntAddMonoid._ foldMonoid[Int](Seq( 1,2,3,4,5,6)) ? 21
- 127. Int / 1 / * import IntMultMonoid._ foldMonoid[Int](Seq( 1,2,3,4,5,6)) ? 720
- 128. String / "" / + foldMonoid[String](Seq(
- 129. Endos / id / ∘ def mash:
- 130. A=>A / a=>a / compose foldMonoid[Int =>
- 131. Are chairs monoids?
- 132. Chair Composition = You can’t turn two chairs into one Identity =
- 133. Chair stack
- 134. Chair stack Composition = stack them on top Identity = no chairs
- 135. Chair Stack is the free monoid
- 136. …almost Real monoids don’t topple; they keep scaling
- 137. Monoids embody the principle of weakly-typed composability
- 138. IV. Products & sums
- 139. Algebraic Data Types List[A] - Cons(A,
- 140. Algebraic Data Types Cons(A
- 141. Algebraic Data Types A ×
- 142. Algebraic Data Types A ×
- 143. Terminology isomorphism
- 144. Terminology isomorphism Equal
- 145. Terminology isomorphism Equal -shape-ism
- 146. Terminology isomorphism “Sorta kinda the same-ish” but
- 147. Terminology isomorphism “Sorta kinda the same-ish” but
- 148. Terminology isomorphism One-to-one mapping between two objects so you can go back-and-forth without losing information
- 149. Isomorphism object object arrows
- 150. Isomorphism Same as identity
- 151. Isomorphism Same as identity
- 152. These 4 Shapes Wiggles Set functions Set
- 153. These 4 Shapes Wiggles
- 154. These 4 Shapes Wiggles
- 155. There can be lots of isos between
- 156. Products A × B A B first
- 157. Sums A + B A B left
- 158. Opposite categories C Cop A B C
- 159. A B C g ∘ f f
- 160. A A×B B A product in C
- 161. Sums ≅ Products!
- 162. Terminology dual An object and its equivalent in the opposite category are to each other.
- 163. Terminology Co-(thing) Often we call something’s dual a
- 164. Terminology Coproducts Sums are also called
- 165. V. Composable systems
- 166. Growing a system Banana
- 167. Growing a system
- 168. Growing a system
- 169. Growing a system Bunch
- 170. Growing a system Bunch Bunch
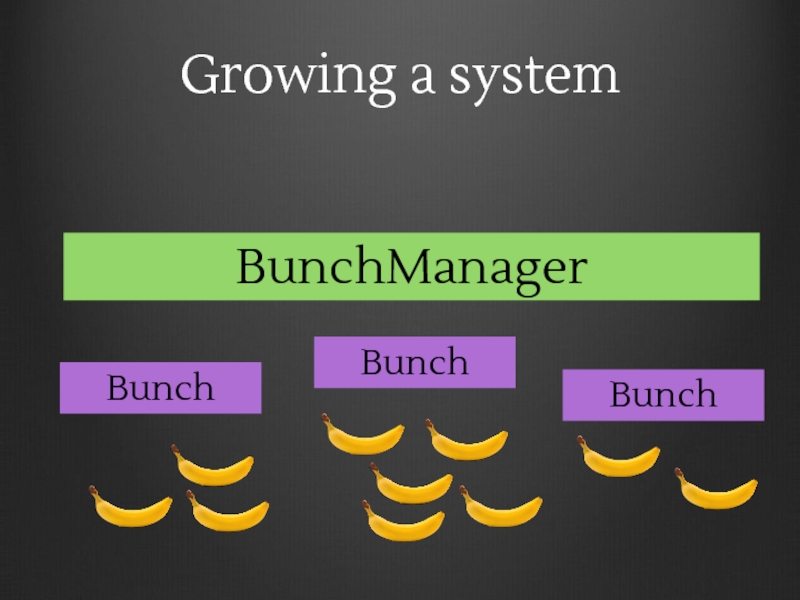
- 171. Growing a system Bunch Bunch Bunch
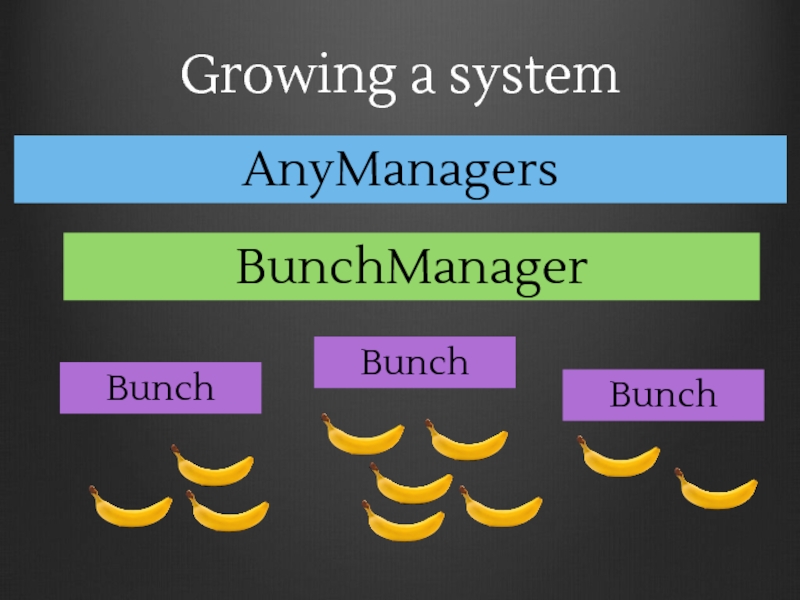
- 172. Growing a system Bunch Bunch Bunch BunchManager
- 173. Growing a system Bunch Bunch Bunch BunchManager AnyManagers
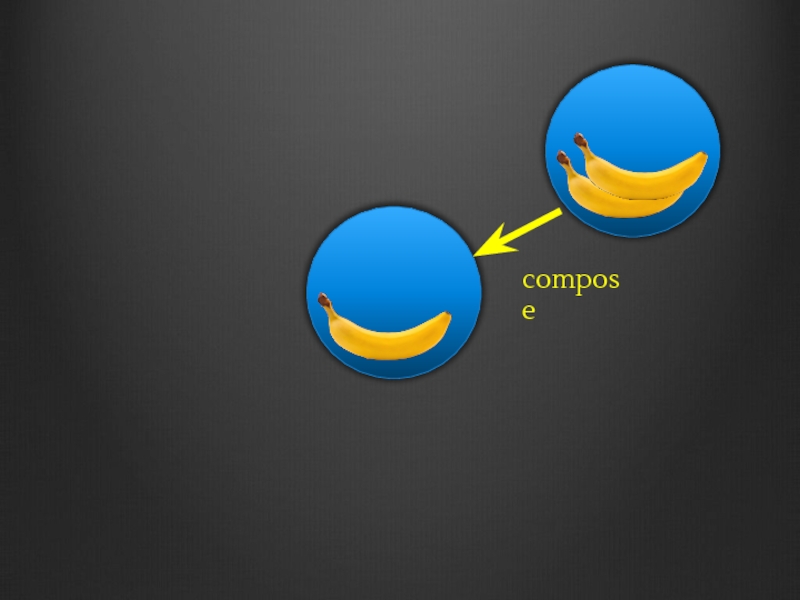
- 177. compose
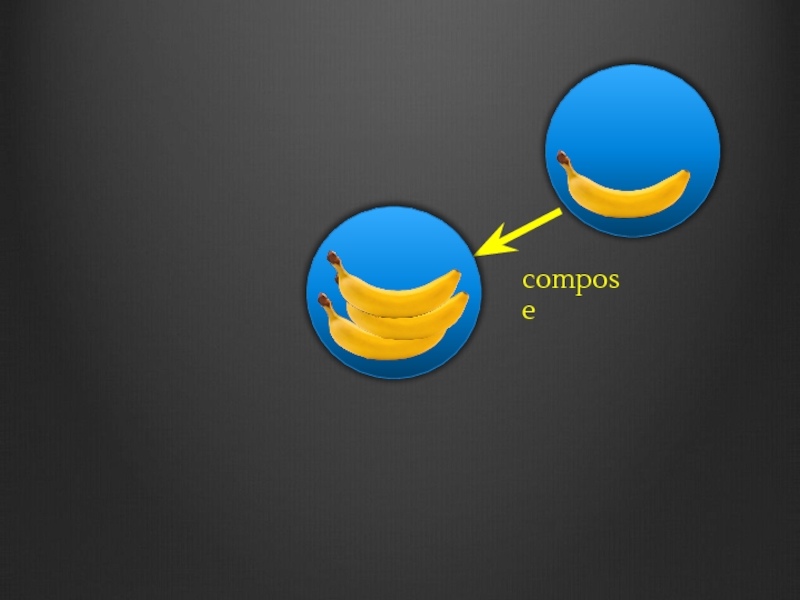
- 179. compose
- 180. etc…
- 181. Using composable abstractions means your code can
- 182. Look for Monoids and Categories in your
- 183. VI. Abstraction
- 184. Spanner
- 185. Spanner AbstractSpanner
- 186. Spanner AbstractSpanner AbstractToolThing
- 187. Spanner AbstractSpanner AbstractToolThing GenerallyUsefulThing
- 188. Spanner AbstractSpanner AbstractToolThing GenerallyUsefulThing AbstractGenerallyUsefulThingFactory
- 189. Spanner AbstractSpanner AbstractToolThing GenerallyUsefulThing AbstractGenerallyUsefulThingFactory WhateverFactoryBuilder
- 191. That’s not what abstraction means.
- 192. Code shouldn’t know things that aren’t needed.
- 193. def getNames(users: List[User]):
- 194. def getNames(users: List[User]):
- 195. def getNames(users: List[User]):
- 196. “Oh, now we need the roster of names! A simple list won’t do.”
- 197. def getRosterNames(users: Roster[User]):
- 198. def getRosterNames(users: Roster[User]):
- 199. def getRosterNames(users: Roster[User]):
- 200. When code knows too much, soon new
- 201. Coupling has increased. The mixed concerns will tangle and snarl.
- 202. Code is rewritten each time for trivially different requirements
- 203. def getNames[F: Functor](users: F[User]):
- 204. Not only is the abstract code not
- 205. Abstraction is about hiding unnecessary information.
- 206. We’ve seen deep underlying patterns beneath superficially different things A×B A+B
- 207. Just about everything ended up being in a category, or being one.
- 208. There is no better way to understand the patterns underlying software than studying Category Theory.
- 209. Further reading Awodey, “Category Theory” Lawvere &
Слайд 2Abstract maths… for us?
Dizzyingly abstract branch of maths
“Abstract nonsense”?
Programming = maths
Programming
Really useful to programming!
Слайд 3The plan
Basic Category Theory concepts
New vocabulary (helpful for further reading)
How it
Category Theory as seen by maths versus FP
Слайд 4A bit of background
1940s Eilenberg, Mac Lane invent Category Theory
1958 Monads
In programming:
1990 Moggi, Wadler apply monads to programming
2006 “Applicative Programming with Effects” McBride & Paterson
2006 “Essence of the Iterator Pattern” Gibbons & Oliveira
Слайд 32Examples
Infinite categories
Finite categories
Objects can represent anything
Arrows can represent anything
As long as
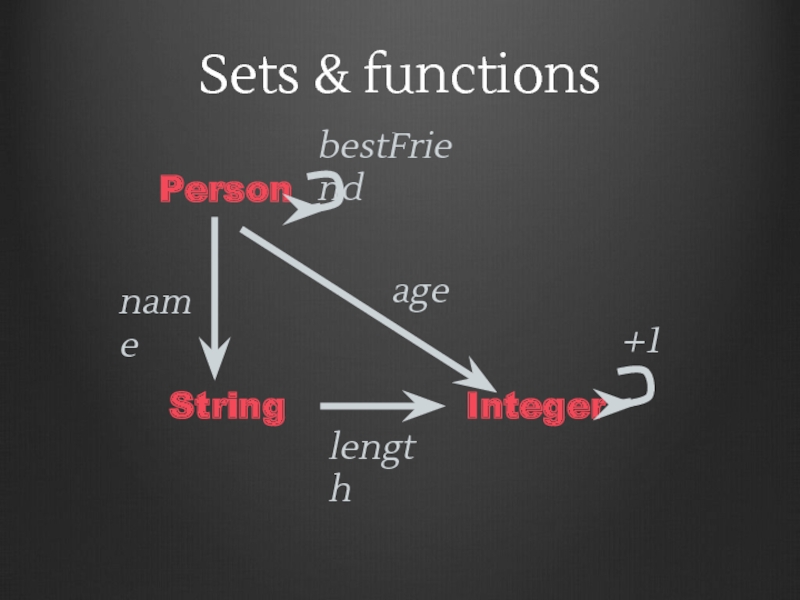
Слайд 34Sets & functions
Infinite arrows from composition
+1∘ length ∘ name
bestFriend ∘ bestFriend
bestFriend
+1∘ age∘ bestFriend
Слайд 36Sets & functions
Objects = sets (or types)
Arrows = functions
Composition = function
Identity = identity function
Слайд 43Class hierarchy
Objects = classes
Arrows = “extends”
Composition = “extends” is transitive
Identity =
Слайд 44Class hierarchy
Partially ordered sets (posets)
Objects = elements in the set
Arrows
Composition = ≤ is transitive
Identity = trivial
Слайд 45World Wide Web
www.naaawcats.com
No dogs allowed!
www.robodogs.com
See here for more robots
www.coolrobots.com
BUY NOW!!!!
Слайд 46World Wide Web
Objects = webpages
Arrows = hyperlinks
Composition = Links don’t compose
Identity
Слайд 48“Free Category” from graphs!
Objects = nodes
Arrows = paths (0 to many
Composition = aligning paths end to end
Identity = you’re already there
Слайд 49Categories in code
trait Category[Arrow[_,_]] {
def compose[A,B,C](
c: Arrow[B,C],
def id[A]: Arrow[A,A]
}
Слайд 50Category of Types & Functions
object FnCat
extends Category[Function1] {
def
a => c(d(a)) }
def id[A]: A => A = (a => a) }
Слайд 51Category of Garden Hoses
sealed trait Hose[In, Out] {
def leaks: Int
def >>[A](in: Hose[A, In]): Hose[A, Out] def <<[A](out: Hose[Out, A]): Hose[In, A]
}
Слайд 55Functors
Functors map between categories
Objects ? objects
Arrows ? arrows
Preserves composition & identity
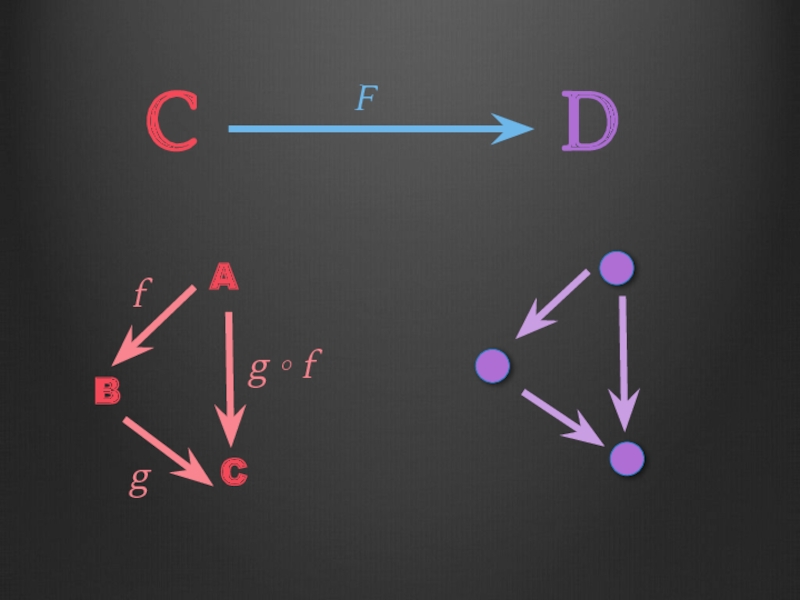
Слайд 59C
F
D
Category
Category
Functor
Cat
Category of categories
Objects = categories
Arrows
Composition = functor composition
Identity = Identity functor
Слайд 90Functors in code
trait Functor[F[_]] {
def map[A,B](fa: F[A],
}
Objects to objects
Слайд 91Functors in code
trait Functor[F[_]] {
def map[A,B](fa: F[A],
}
Arrows to arrows
Слайд 92Functors in code
trait Functor[F[_]] {
def map[A,B]:
(A =>
}
Arrows to arrows
Слайд 100Endofunctors
In Scala, all our functors are
actually endofunctors.
Type
F
Category
Category
Endofunctor
Type
Слайд 101Endofunctors
Luckily, we can represent any functor in our type system as
Type
F
Category
Category
Endofunctor
Type
Слайд 102List Functor
sealed trait List[+A]
case class Cons(head: A, tail: List[A])
extends
case object Nil extends List[Nothing]
Слайд 103List Functor
sealed trait List[+A] {
def map[B](f: A => B): List[B]
Слайд 106Other functors
trait Tree[A]
trait Future[A]
trait Process[A]
trait Command[A]
X => A
(X, A)
trait Option[A]
Слайд 107Functors
Fundamental concept in Category Theory
Super useful
Everywhere
Staple of functional programming
Write code that’s
Слайд 117Monoids are categories
Objects = placeholder singleton
Arrows
Composition = •
Identity = id
Only one object
Each arrow is an element in the monoid
Слайд 120M
H
N
Monoid
Monoid
Monoid homomorphism
(SM, •M, idM)
(SN, •N, idN)
Mon
Category of monoids
Objects
Arrows = monoid homomorphisms
Composition = function composition
Identity = Identity function
Слайд 121M
H
N
SM
SN
“structure-preserving map”
Set
Set
function
h
Sets
Where h preserves composition & identity
Слайд 123Preserves identity
Preserves composition
"".length == 0
(str1 + str2).length = str1.length + str2.length
Слайд 125Monoids in code
def foldMonoid[M: Monoid](
ms: Seq[M]): M = {
}
Слайд 129Endos / id / ∘
def mash: Potato => Potato
def addOne: Int
def flipHorizontal: Shape => Shape
def bestFriend: Person => Person
Слайд 130A=>A / a=>a / compose
foldMonoid[Int => Int](Seq(
_ + 12,
_
? (n: Int) => ((n + 12) * 2) - 3
Слайд 135Chair Stack is the
free monoid of chairs
Protip: just take 0-to-many
Слайд 139Algebraic Data Types
List[A]
- Cons(A, List[A])
- Nil
Option[A]
- Some(A)
-
BusinessResult[A]
- OK(A)
- Error
Wiggles
- YellowWiggle
- BlueWiggle
- RedWiggle
- PurpleWiggle
Address(Street, Suburb,
Postcode, State)
Слайд 140Algebraic Data Types
Cons(A × List[A])
+ Nil
Some(A)
OK(A)
+ Error
YellowWiggle
+ BlueWiggle
+ RedWiggle
+ PurpleWiggle
Street × Suburb × Postcode × State
Слайд 142Algebraic Data Types
A × List[A] + 1
A +
A + 1
4
Street × Suburb × Postcode × State
isomorphic
Слайд 146Terminology
isomorphism
“Sorta kinda the same-ish” but I want to sound really smart
-
Слайд 147Terminology
isomorphism
“Sorta kinda the same-ish” but I want to sound really smart
-
Слайд 148Terminology
isomorphism
One-to-one mapping between two objects so you can go back-and-forth without
Слайд 155There can be lots of isos between two objects!
If there’s at
or A ≅ B
Слайд 181Using composable abstractions means your code can grow without getting more
Categories and Monoids capture the essence of composition in software!
Слайд 182Look for Monoids and Categories in your domain where you can
You
Слайд 188Spanner
AbstractSpanner
AbstractToolThing
GenerallyUsefulThing
AbstractGenerallyUsefulThingFactory
Слайд 189Spanner
AbstractSpanner
AbstractToolThing
GenerallyUsefulThing
AbstractGenerallyUsefulThingFactory
WhateverFactoryBuilder
Слайд 194def getNames(users: List[User]):
Over time…
Слайд 195def getNames(users: List[User]):
} else { users.map(_.name) } }
Слайд 198def getRosterNames(users: Roster[User]):
Over time…
Слайд 199def getRosterNames(users: Roster[User]):
Слайд 200When code knows too much, soon new things will appear that
Слайд 203def getNames[F: Functor](users: F[User]):
getNames(List(alice, bob, carol))
getNames(Roster(alice, bob, carol))
Слайд 204Not only is the abstract code not weighed down with useless
Reusable out of the box!
Слайд 205
Abstraction is about hiding unnecessary information. This a good thing.
We actually
Слайд 208There is no better way to understand the patterns underlying software
Слайд 209Further reading
Awodey, “Category Theory”
Lawvere & Schanuel, “Conceptual Mathematics: an introduction to
Jeremy Kun, “Math ∩ Programming” at http://jeremykun.com/
Gabriel Gonzalez “Haskell for all”
http://www.haskellforall.com/2012/08/the-category-design-pattern.html
http://www.haskellforall.com/2014/04/scalable-program-architectures.html

























![Categories in codetrait Category[Arrow[_,_]] { def compose[A,B,C]( c: Arrow[B,C], d: Arrow[A,B]): Arrow[A,C] def](/img/tmb/2/162309/bc57aabba84b4bcdc585739035171131-800x.jpg)
![Category of Types & Functionsobject FnCat extends Category[Function1] { def compose[A,B,C]( c: B](/img/tmb/2/162309/a1b7df9b24fe7b089462e12d8553f227-800x.jpg)
![Category of Garden Hosessealed trait Hose[In, Out] { def leaks: Int def kinked: Boolean def](/img/tmb/2/162309/d2e205952d0a7f3f0d38590af1241fb3-800x.jpg)
![Category of Garden Hoses[live code example]](/img/tmb/2/162309/73066d57e8aeb43b334e0464d36b0984-800x.jpg)

















![Functors in codetrait Functor[F[_]] { def map[A,B](fa: F[A], f: A =>](/img/tmb/2/162309/20851b33665b1b81b7eaed155800c92d-800x.jpg)
![Functors in codetrait Functor[F[_]] { def map[A,B](fa: F[A], f: A =>](/img/tmb/2/162309/046b39fbc284629f1b3c7e1293e4010c-800x.jpg)
![Functors in codetrait Functor[F[_]] { def map[A,B](fa: F[A], f: A =>](/img/tmb/2/162309/ef9ccfd9d27b63125d3b9fff48dd6c84-800x.jpg)
![Functors in codetrait Functor[F[_]] { def map[A,B]: (A => B) => (F[A] => F[B])}Arrows](/img/tmb/2/162309/e208767c4b8fd2e090fd41f0b8df0b84-800x.jpg)








![EndofunctorsLuckily, we can represent any functor in our type system as some F[_]TypeFCategoryCategoryEndofunctorType](/img/tmb/2/162309/57bc31361f7b506f8005f0bafafcdca3-800x.jpg)
![List Functorsealed trait List[+A]case class Cons(head: A, tail: List[A]) extends List[A]case object Nil extends List[Nothing]](/img/tmb/2/162309/84142fef47b07d8f13782993c10e5e8b-800x.jpg)
![List Functorsealed trait List[+A] { def map[B](f: A => B): List[B] = this match](/img/tmb/2/162309/2a9d8e1b4c72814739fed5c385b42a91-800x.jpg)


![Other functorstrait Tree[A]trait Future[A]trait Process[A]trait Command[A]X => A(X, A)trait Option[A]](/img/tmb/2/162309/d26ad66fbd88775f954f715b241cb4db-800x.jpg)














![Monoids in codetrait Monoid[M] { def compose(a: M, b: M): M def id: M}](/img/tmb/2/162309/beb045206057d368534afbb79713487f-800x.jpg)
: M = { ms.foldLeft(Monoid[M].id) (Monoid[M].compose)}](/img/tmb/2/162309/7981b122829dd94ec4958bb4d52f8360-800x.jpg)
)? 21](/img/tmb/2/162309/368c09ac9b2e09e095f23e286470ac8b-800x.jpg)
)? 720](/img/tmb/2/162309/27a21c7171cd0d234fd82feb2aed9ac4-800x.jpg)











![Algebraic Data TypesList[A] - Cons(A, List[A]) - NilOption[A] - Some(A) - NoneBusinessResult[A] - OK(A) -](/img/tmb/2/162309/20beeb0910e314130a924ff6c600a7d3-800x.jpg)
![Algebraic Data Types Cons(A × List[A]) + Nil Some(A) + None OK(A) +](/img/tmb/2/162309/c42bf230c934463a04df868da666a032-800x.jpg)
![Algebraic Data Types A × List[A] + 1 A + 1 A + 14Street](/img/tmb/2/162309/9ad63f20898bbdc319ca5dd9276f772d-800x.jpg)
![Algebraic Data Types A × List[A] + 1 A + 1 A + 14Street](/img/tmb/2/162309/77a33ebaeb10c8fba0b83e3fd05e17b1-800x.jpg)






































![def getNames(users: List[User]): List[Name] = { users.map(_.name) }](/img/tmb/2/162309/c5c2766a45a80f8f540c6f9635756c9d-800x.jpg)
![def getNames(users: List[User]): List[Name] = { println(users.length) users.map(_.name)](/img/tmb/2/162309/08ce64a8b832d93c2c89563cd9a94993-800x.jpg)
![def getNames(users: List[User]): List[Name] = { println(users.length) if](/img/tmb/2/162309/b6e89b77c1d0bf2edc577b922eb28a91-800x.jpg)

![def getRosterNames(users: Roster[User]): Roster[Name] = { users.map(_.name) }](/img/tmb/2/162309/8cbd603e459bd98bbecc859f9a50a394-800x.jpg)
![def getRosterNames(users: Roster[User]): Roster[Name] = { LogFactory.getLogger.info(s”When you](/img/tmb/2/162309/defb27eaaca1cd96b528a080fde4a170-800x.jpg)
![def getRosterNames(users: Roster[User]): Roster[Name] = { LogFactory.getLogger.info(s](/img/tmb/2/162309/3c14ceade0b261d97c5653a44925d380-800x.jpg)



: F[Name] = { Functor[F].map(users)(_.name)](/img/tmb/2/162309/e504111de66462ec816d0964559fc8bd-800x.jpg)











