ТПР . Многопараметрические методы оптимизации. (Занятие 5) презентация

с Вами приступили к изучению много-параметрических методов оптимизации, рассмотрели аналитический метод в многомерном пространстве (правда, довольно поверхностно) и договорились о том, каким графическим приёмом мы будем пользо-ваться для иллюстрации методов, следующих далее.
Двинемся дальше, вернее ниже, если обратиться
к показанному слева фрагменту классификации.

Метод Гаусса-Зайделя

Карл Фридрих Гаусс (1777-1855)
Немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков всех времён, «королём математиков».

Филипп Людвиг фон Зайдель (1821 – 1896)
Немецкий математик. Его именем назван один из лунных кратеров.

каждой серии следует с заданным шагом изменять только один из факторов,
а остальные факторы сохранять неизменными.

Серию надо продолжать до тех пор, пока движение приводит к улучшению
критерия оптимизации

Если критерий оптимизации начал ухудшаться, серию надо остановить,
выбрать тот из опытов, который дал наилучший результат, и использовать
его координаты для планирования новой серии, в которой изменяться
будет уже другой фактор.

Если изменение любого из факторов приводит к ухудшению результата,
можно принять одно из двух решений:
успокоиться на этом и считать оптимальными координаты того опыта,
который дал наилучшее значение критерия;
если ресурсы не исчерпаны и Заказчик требует дальнейшего улучшения,
можно продолжить поиск в окрестности найденного экстремума,
уменьшив шаги движения.

1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1-й опыт дал улучшение
критерия. Продолжим
серию

1

1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

2-й опыт дал улучшение
критерия. Продолжим
серию

1

2

1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

3-й опыт дал улучшение
критерия. Продолжим
серию

1

2

3

1-й серии:
Начальная точка А с координатами Х1А, Х2А
Изменяется фактор Х2 (Х2 = varium), а фактор Х1 сохраняется неизменным (Х1 = idem)
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

4-й опыт дал ухудшение
критерия. Останавливаем
первую серию

1

2

3

4

2-й серии:
Начальная точка 3
Изменяется фактор Х1 (Х1 = varium), а фактор Х2 сохраняется неизменным (Х2 = idem)
Для изменения фактора Х1 назначается шаг ΔХ1

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

Опыты с 5 по 8 дали
улучшение критерия, а
9-й его ухудшил.
Планируем третью серию

1

2

3

4

5

6

7

8

9

3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

А вот куда двигаться:
вверх или вниз? Форма
«горы» нам априори не
известна, поэтому выби-
раем наугад. Допустим,
решили двигаться вверх.
Увы, опыт 10 ухудшил
результат.

1

2

3

4

5

6

7

8

9

10

3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

Стало быть, наш выбор
не удачен. Поменяем
направление на
противоположное
(опыт 11).

1

2

3

4

5

6

7

8

9

10

11

3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

Продолжая действовать
в том же духе, убедимся
в том, что движение в
любую сторону от точки 11 приводит к ухудше-нию критерия. Тут надо
принимать одно из двух решений:

1

2

3

4

5

6

7

8

9

10

11

13

12

14

3-й серии:
Начальная точка 8
Х2 = varium, Х1 = idem
Для изменения фактора Х2 назначается шаг ΔХ2

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1. Остановить поиск и считать координаты точки 11 оптимальным сочета-нием значений парамет-ров Х1 и Х2.
2. Продолжить поиск в
окрестности точки 11, уменьшив шаги ΔХ1 и ΔХ2

1

2

3

4

5

6

7

8

9

10

11

13

12

14

позволили целиком пройти весь путь к оптимуму, Вы всё-же частично
улучшите исходное состояние объекта (если, конечно, это в принципе возможно).

Метод адаптивен к свойствам объекта, т.е. он обеспечивает автоматический разворот
направления поиска в сторону оптимального решения.

Метод устойчив, т.е. неправильный выбор направления движения временно ухудшает
ситуацию, но затем алгоритм поиска обеспечивает автоматическую корректировку
траектории движения.

Метод, в принципе, способен обеспечить сколь угодно точное нахождение оптимума
путём соответствующего выбора шагов изменения факторов (разумеется, если Вы
располагаете неограниченным запасом ресурсов, времени и терпения).

Недостатки метода Гаусса-Зайделя

Слишком длинный путь к оптимуму, особенно, при большом количестве факторов.
Если это чисто математический малозатратный поиск, то это не так критично, но если
определение значений критерия при каждой заданной комбинации значений
факторов требует проведения реальных экспериментов и испытаний, медленный путь
к оптимуму обернётся большими затратами времени и ресурсов.

Если в зоне поиска имеется несколько экстремумов, то метод не гарантирует выход
на самый благоприятный из них.

горы по кусочно-линейной траектории,
содержащей только широтные (запад-восток) и меридиональные (север-юг) участки.
Наверное, они очень нескоро водрузят победный флаг на вершине.

Нельзя ли как-то сократить этот путь?
Понятно, что кратчайшей траекторией была бы прямая, соединяющая отправную точку
с вершиной. Но реальным альпинистам так двигаться не позволяет сложная форма
склонов. Да и вершина горы людям, стоящим у её подножья, обычно не видна.
Тем не менее, можно форсировать восхождение, если осмотреться вокруг
и начать движение в направлении наиболее крутого склона.

Нам с Вами форма склонов нашей математической горы помешать не может, а вот
второе препятствие значимо и для нас: мы тоже не видим вершину.
Ну что же, давайте поступим аналогичным образом: изучим свойства нашего объекта в
окрестности отправной точки и будем двигаться в том направлении, в котором функция
K = f(X1, X2) изменяется с максимальной скоростью.

Вектор, указывающий направление наибольшей интенсивности изменения функции,
математики называют градиентом. Значит, и придуманный нами метод, можно назвать
градиентным.

Справедливости ради надо указать, что его ещё раньше – в 1951 году – предложили
Box и Wilson. С тех пор его так и называют: метод Бокса-Уилсона. А также метод «крутого
восхождения» (если нужен максимум критерия) или «наискорейшего спуска» (если
нужен минимум).

свойств объекта в окрестности точки А
проведём начальную серию опытов в соответствие
с планом полного факторного эксперимента на двух
уровнях (опыты 1÷4). Полученная матрица:

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

3

2

4

матрицы можно вычислить коэффициенты
регрессии, характеризующие силу влияния факторов
Х1 и Х2 на величину критерия К:
В1=(+К1-К2+К3-К4)/4 В2=(+К1+К2-К3-К4)/4

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

3

2

4

90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

3

2

4

90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

3

2

4

7 значение критерия стало хуже, чем в точке 6. Поэтому на этом процесс останавливаем, и считаем оптимальным сочетанием значений факторов Х1 и Х2 координаты точки 6.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

3

2

4

δ1

δ2

5

6

7

существенное
сокращение количество опытов (по сравнению с методом Гаусса-Зайделя).

Метод не адаптивен к свойствам объекта, т.е. он не обеспечивает автоматический
разворот направления поиска в сторону оптимального решения. Движение происходит
строго в направлении градиента, определённого в окрестности исходной точки.

Метод не обеспечивает сколь угодно точное нахождение оптимума по двум
причинам:
− погрешности, допущенные при проведении предварительного плана эксперимента,
приведут к тому, что выбранное направление движения будет несколько отличаться
от направления градиента;
− направление градиента, даже совершенно точно определённое, далеко не всегда
совпадает с направлением на экстремум. Степень расхождения зависит от свойств
объекта:

Недостатки метода Бокса-Уилсона

Примечание:
градиент всегда направлен
по нормали к линии
равного уровня

в n-мерном факторном пространстве.

В 2-х мерном пространстве это плоская фигура с 3-мя вершинами, т.е. треугольник.
В 3-х мерном пространстве это объёмная фигура с 4-мя вершинами, т.е. тетраэдр.
В гиперпространстве с числом измерений больше 3-х это гипертетраэдр.

Симплексы бывают правильными и неправильными (например, в 2-х мерном простран-
стве правильный симплекс − это равносторонний треугольник).
В рассматриваемом методе симплексы (и правильные и неправильные) используются
для построения траектории движения к оптимуму. Правильные применяют чаще,
поскольку их удобнее строить и проще вычислять координаты их вершин. Не будем
и мы нарушать эту традицию.

Основные этапы симплексного метода

В факторном пространстве в окрестности исходной точки строят начальный симплекс
и проводят опытное (или расчётное) определение значений критерия оптимизации
для комбинаций значений факторов, заданных координатами вершин симплекса.

Следующий симплекс достраивают вплотную к исходному путём зеркального отражения
относительно противоположной грани вершины исходного симплекса, давшей
наихудшее значение критерия.

Процедуры достраивания симплексов продолжают до тех пор, пока они приводят
к улучшению значения критерия оптимизации.

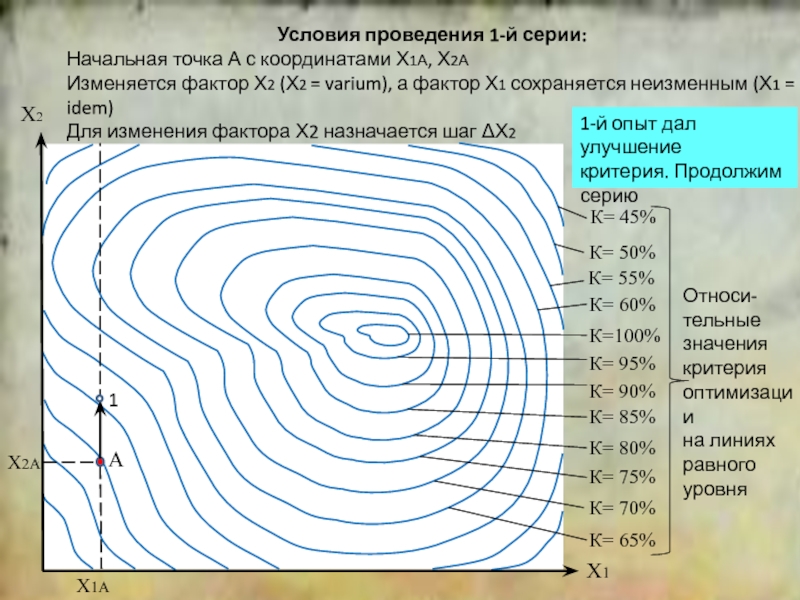
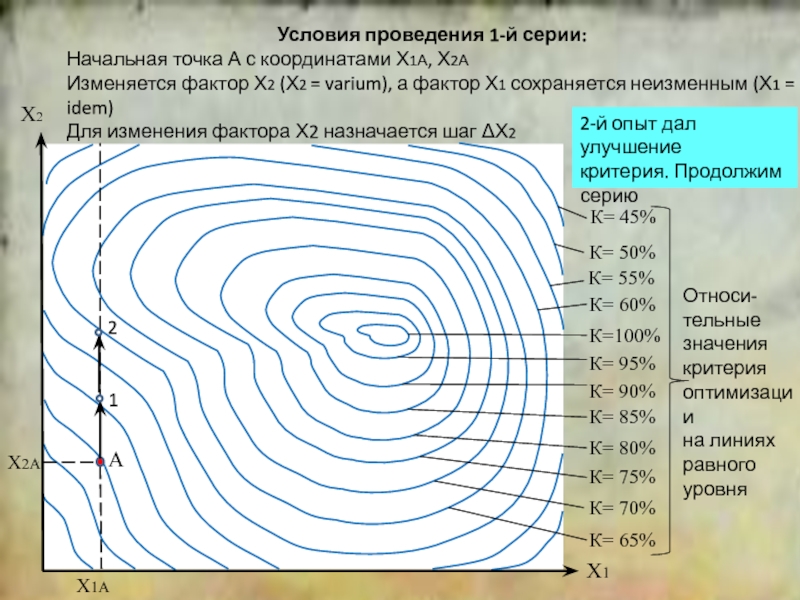
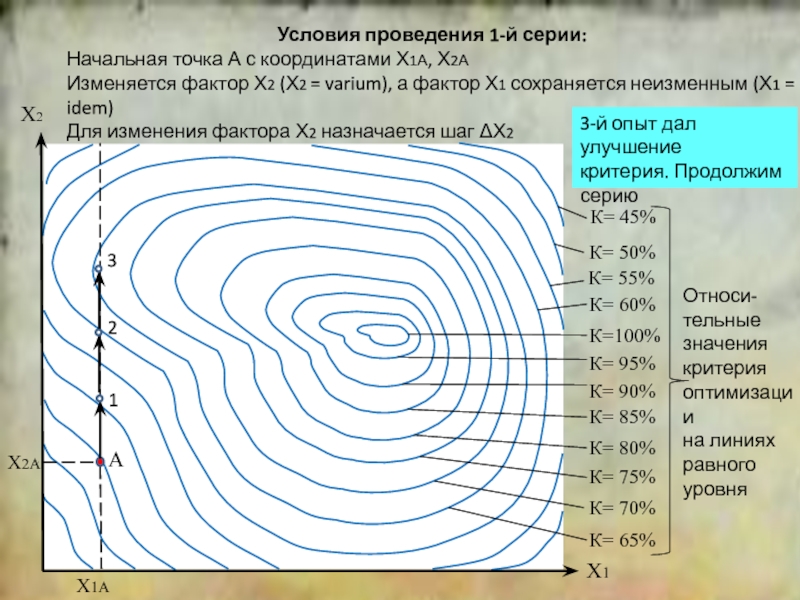
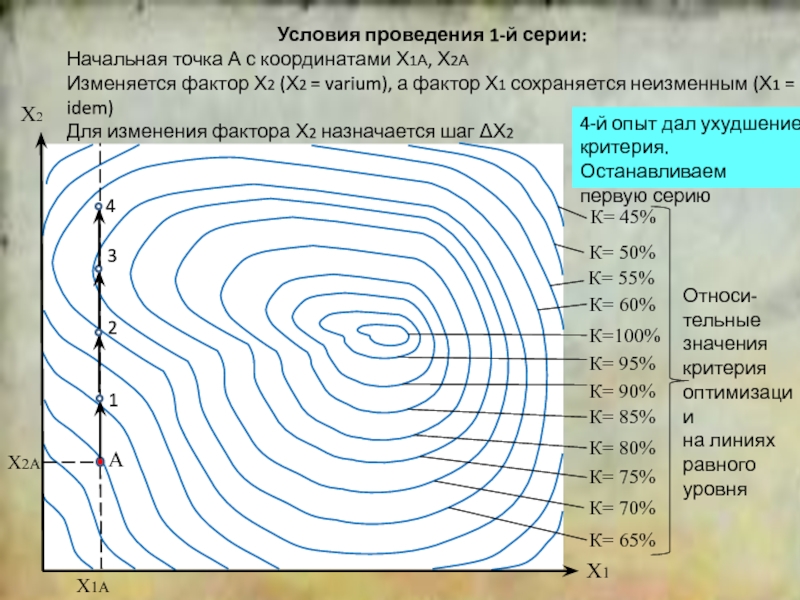
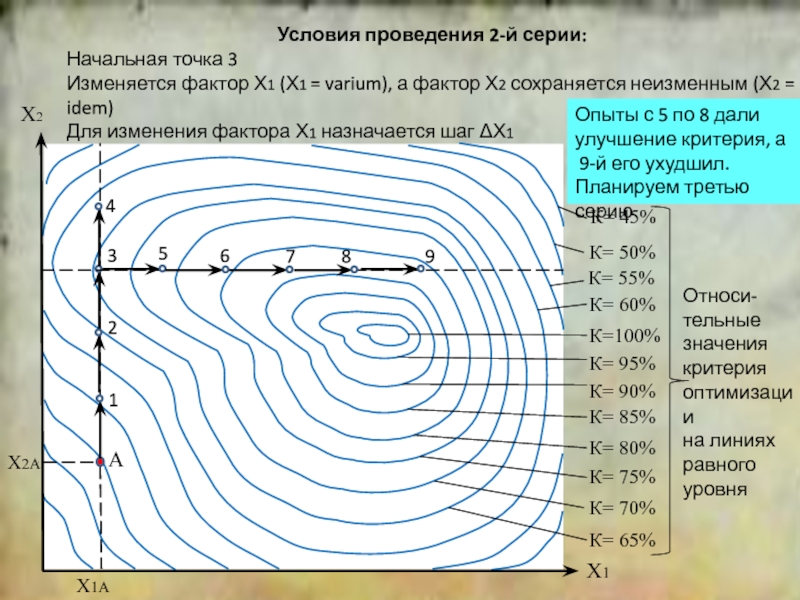
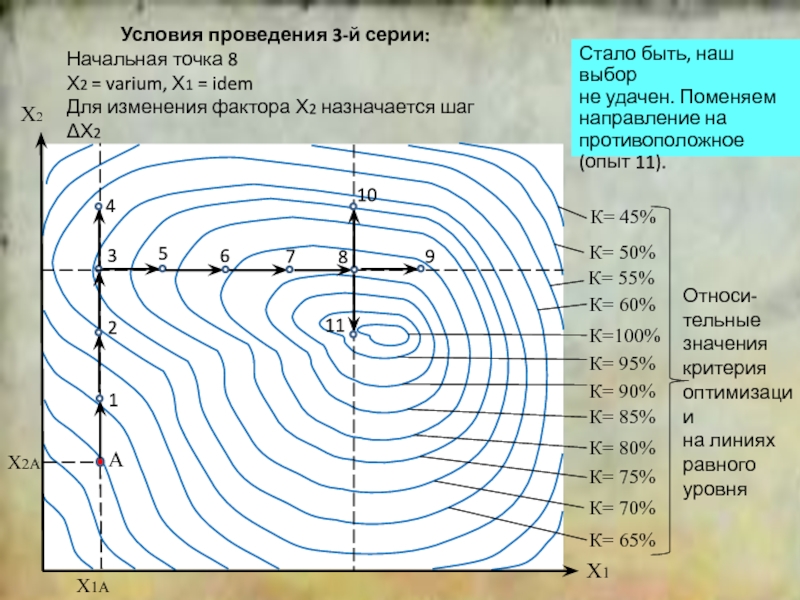
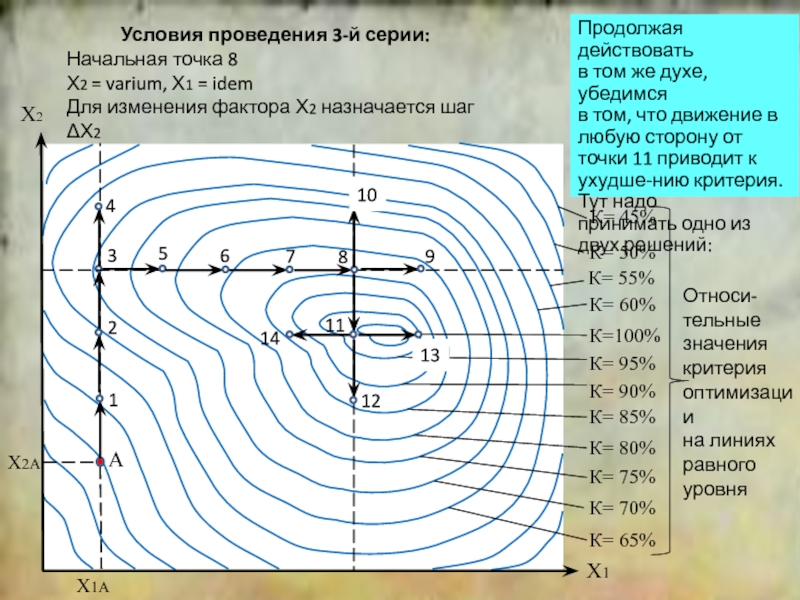
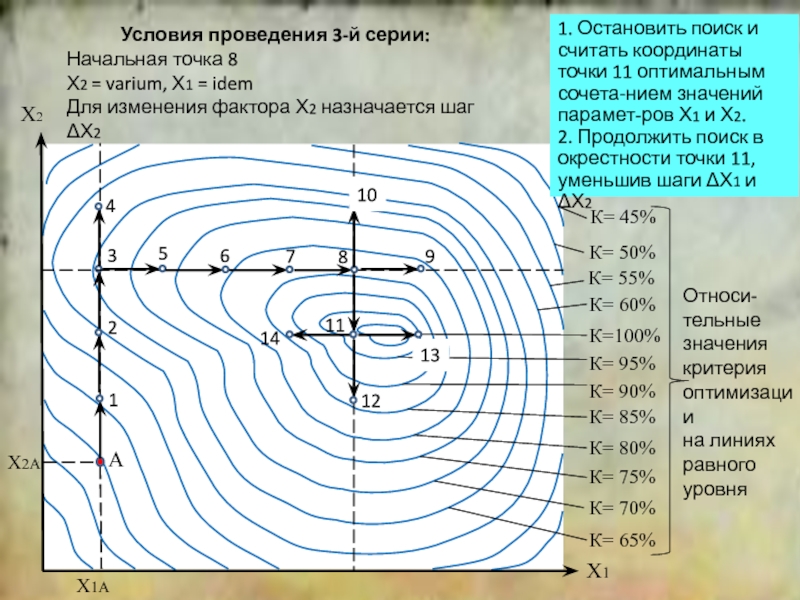
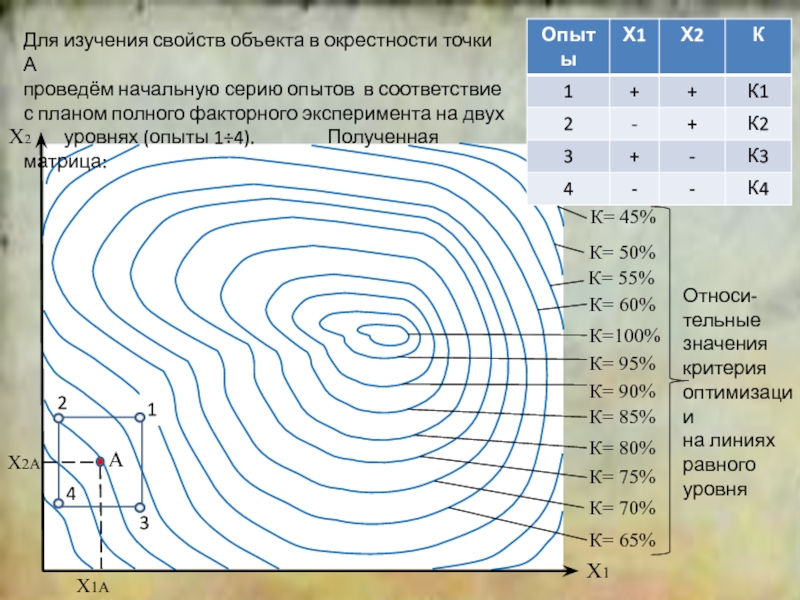
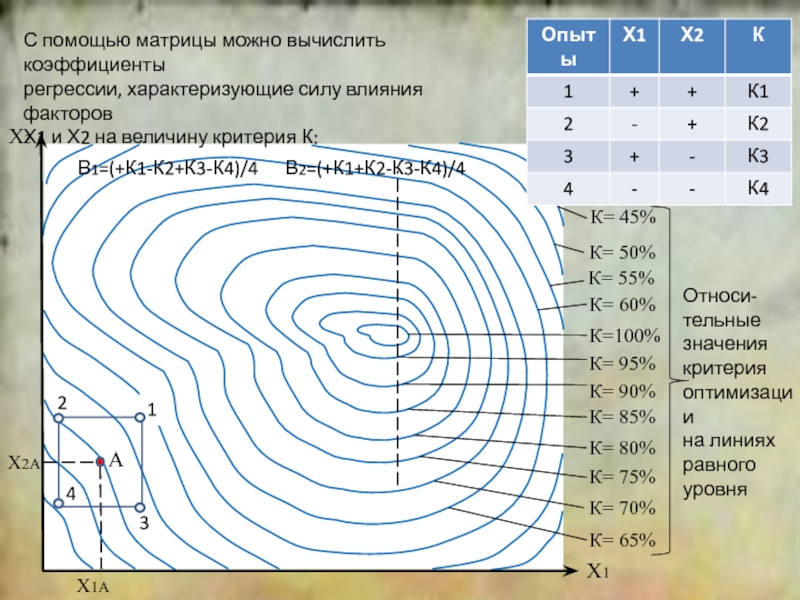
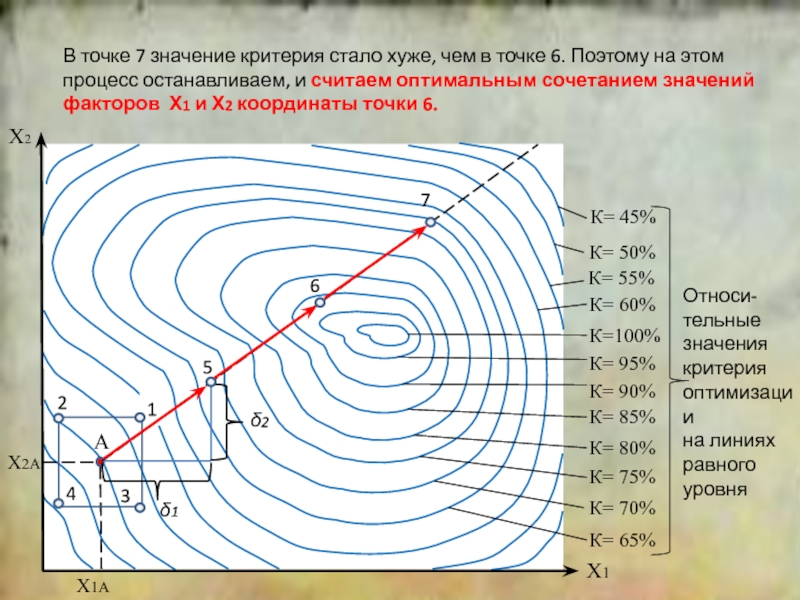
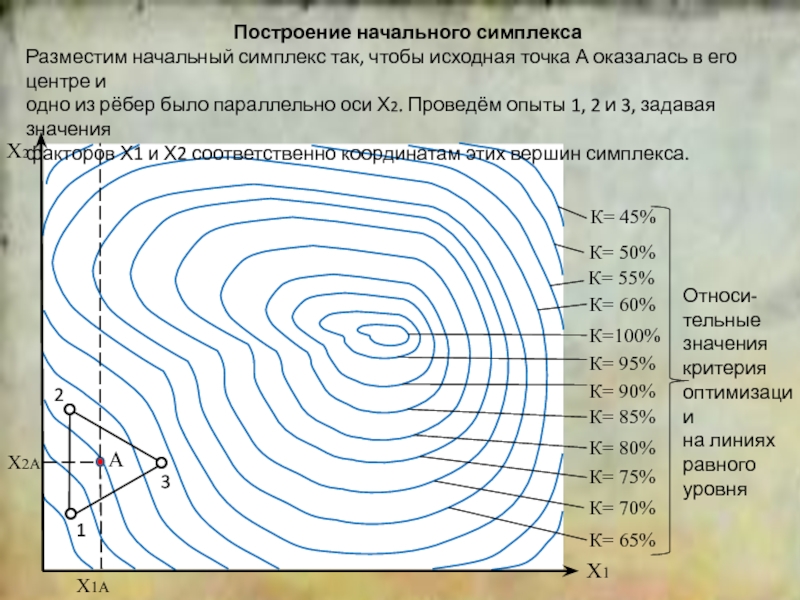
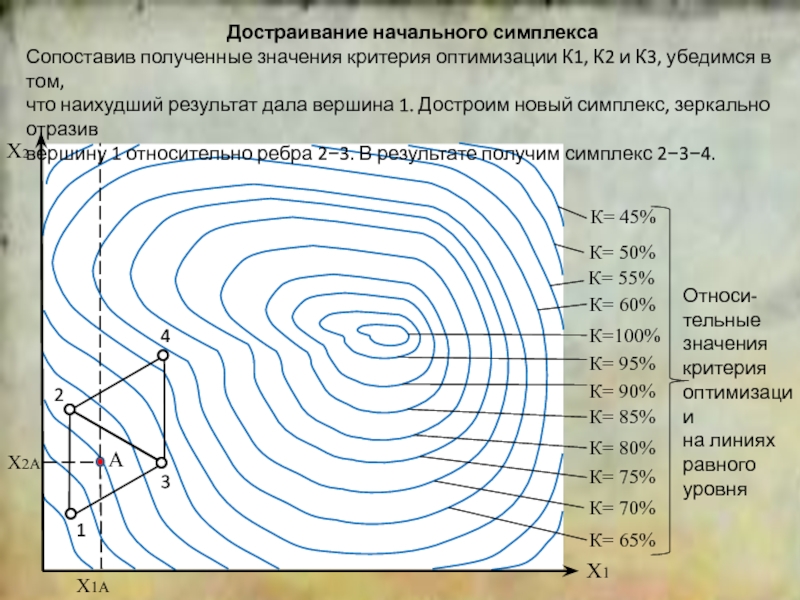
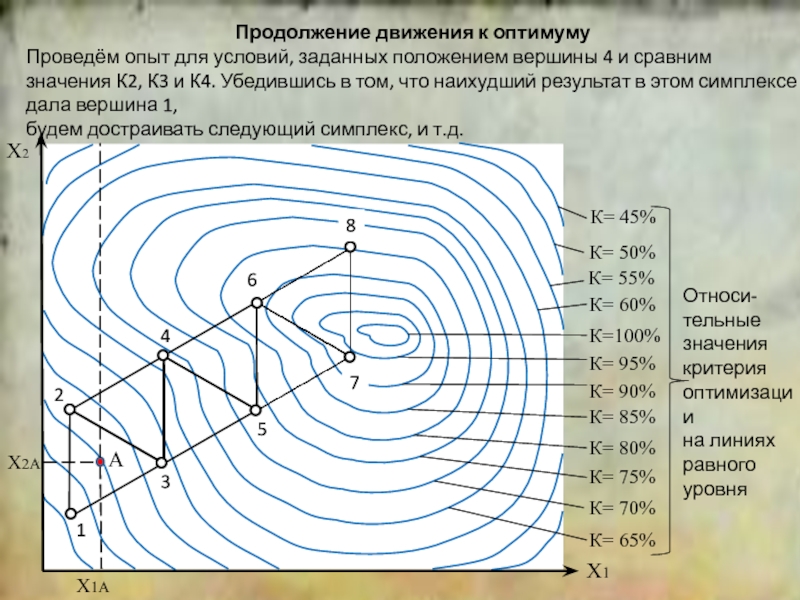
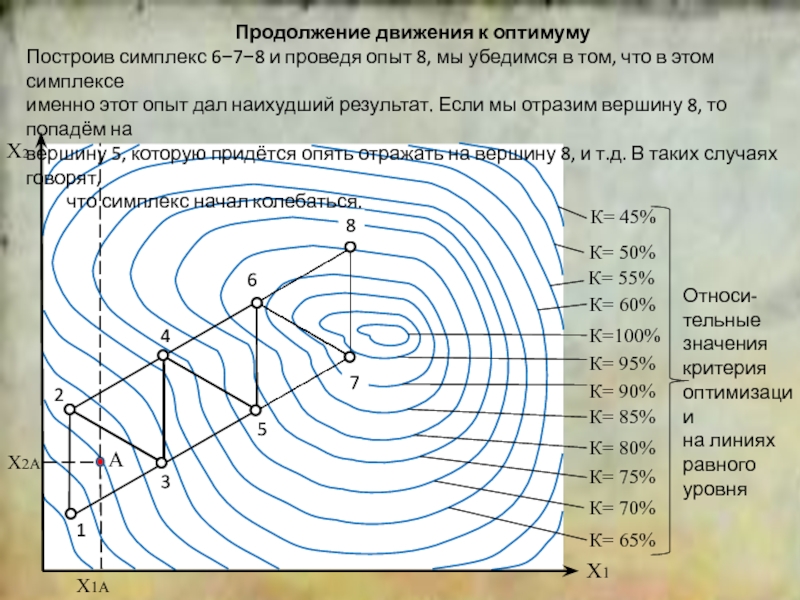
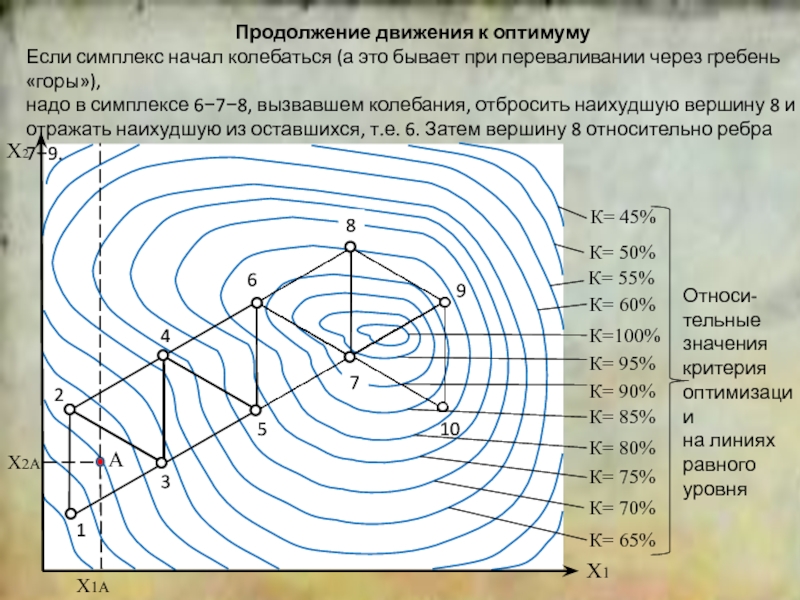
положение симплекса относительно исходной точки.
Строгая теория советует располагать начальный симплекс так, чтобы исходная точка
находилась в центре симплекса. Если речь идёт о малорасходном математическом
эксперименте, следует придерживаться этой рекомендации.
Если же проведение каждого опыта требует существенных затрат времени и ресурсов,
можно немножко сэкономить и то и другое, если одну из вершин симплекса поместить
в исходную точку, для которой значение критерия оптимизации уже известно.

Наконец, надо задать ориентацию начального симплекса относительно осей координат.
Вообще говоря, она может быть произвольной, но для удобства построения и вычисления
координат вершин, лучше расположить начальный симплекс так, чтобы одно из его рёбер
было параллельно одной из осей координат.

Затем, надо задать его размер начального симплекса: слишком большой симплекс даст очень приблизительную оценку координат оптимума, слишком мелкий размер приведёт к неоправданному увеличению числа опытов. Приемлемый компромисс, как правило,
достигается, если размер ребра симплекса составляет примерно 10% от диапазона
области оптимизации.

Прежде всего, надо определиться, какой симплекс мы будем использовать: правильный
или неправильный. Выберем правильный.

симплекса
Разместим начальный симплекс так, чтобы исходная точка А оказалась в его центре и
одно из рёбер было параллельно оси Х2. Проведём опыты 1, 2 и 3, задавая значения
факторов Х1 и Х2 соответственно координатам этих вершин симплекса.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

симплекса
Сопоставив полученные значения критерия оптимизации К1, К2 и К3, убедимся в том,
что наихудший результат дала вершина 1. Достроим новый симплекс, зеркально отразив
вершину 1 относительно ребра 2−3. В результате получим симплекс 2−3−4.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

4

к оптимуму
Проведём опыт для условий, заданных положением вершины 4 и сравним значения К2, К3 и К4. Убедившись в том, что наихудший результат в этом симплексе дала вершина 1,
будем достраивать следующий симплекс, и т.д.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

4

5

6

7

8

к оптимуму
Построив симплекс 6−7−8 и проведя опыт 8, мы убедимся в том, что в этом симплексе
именно этот опыт дал наихудший результат. Если мы отразим вершину 8, то попадём на
вершину 5, которую придётся опять отражать на вершину 8, и т.д. В таких случаях говорят,
что симплекс начал колебаться.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

4

5

6

7

8

к оптимуму
Если симплекс начал колебаться (а это бывает при переваливании через гребень «горы»),
надо в симплексе 6−7−8, вызвавшем колебания, отбросить наихудшую вершину 8 и
отражать наихудшую из оставшихся, т.е. 6. Затем вершину 8 относительно ребра 7−9.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

4

5

6

7

8

9

10

мы получили ещё одну характерную ситуацию: симплексы стали крутиться вокруг точки 7. Это является явным признаком того, что мы уже находимся в районе вершины.
Тут опять надо принимать одно из решений: или успокоиться на этом и считать координаты точки 7 оптимальным сочетанием значений факторов Х1 и Х2, или продол-
жить поиск в окрестности вершины, уменьшив размер симплекса.

К=100%

К= 95%

К= 90%

К= 85%

К= 80%

К= 75%

К= 70%

К= 65%

К= 50%

К= 60%

К= 45%

К= 55%

1

2

3

4

5

6

7

8

9

10

улучшение результатов.
Адаптивность к свойствам объекта.
Устойчивость к случайным сбоям (если в результате ошибочно проведённого опыта отражена будет не та вершина, траектория сделает шаг в сторону, но далее опять развернётся в нужном направлении (если, конечно, Вы не будете совершать грубые ошибки во всех опытах подряд).
Изменяя размер симплекса тоже можно, как и в методе Гаусса-Зайделя, добиться нужной точности решения оптимизационной задачи.
По сравнению с методом Гаусса-Зайделя, симплексный метод быстрее приводит к оптимуму (при правильном выборе размера симплекса). Правда, всё-таки не так
быстро, как градиентный. То есть, по этому показателю он занимает промежуточ-
ное положение между методами Гаусса-Зайделя и Бокса-Уилсона.

Наша следующая тема − многокритериальная оптимизация.
Но это уже через неделю. А пока − до свидания!