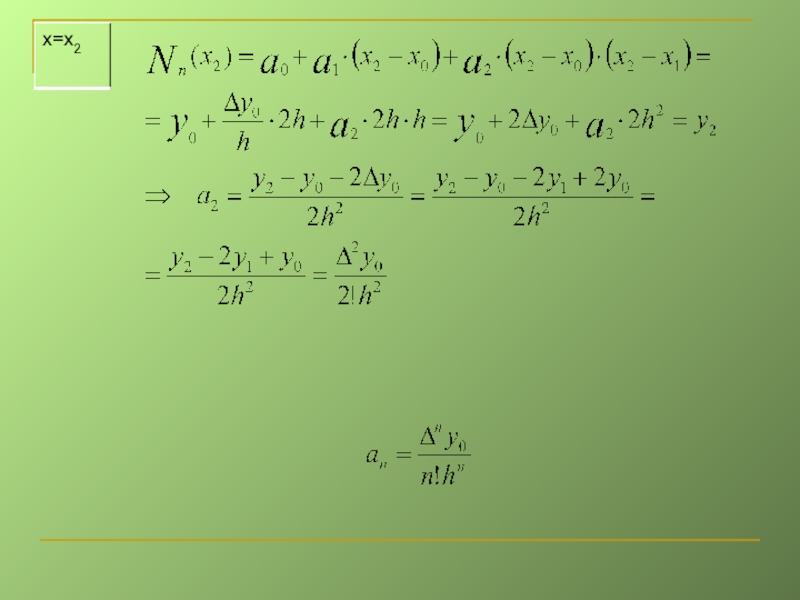- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Інтерполяційний многочлен Ньютона. (Лекція 3) презентация
Содержание
- 1. Інтерполяційний многочлен Ньютона. (Лекція 3)
- 2. 3.Нехай задана таблична функція:
- 3. Таблиця кінцевих різниць різних порядків
- 4. Приклад 1. Кожне число цієї
- 5.
- 6.
- 7.
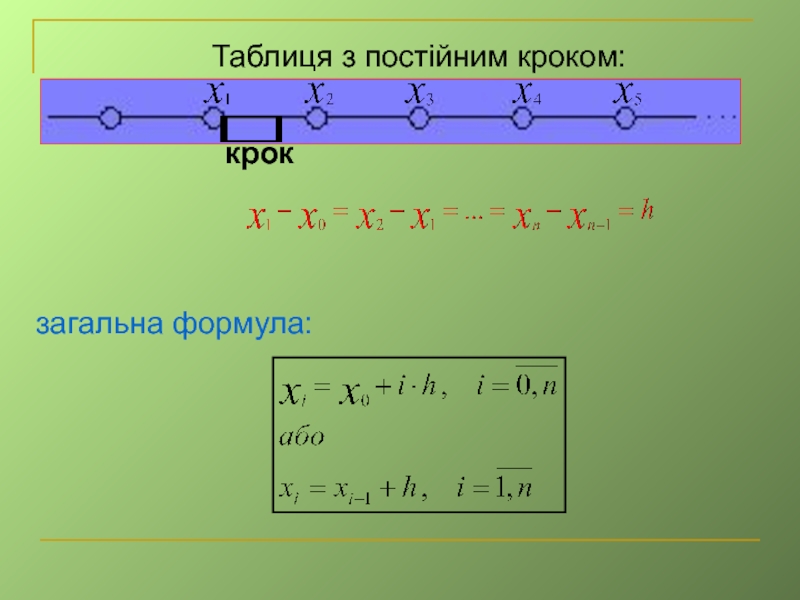
- 8. Таблиця з постійним кроком:
- 9. Розділені різниці для таблиці з постійним кроком:
- 10. 5.Інтерполяційний многочлен Ньютона Розглянемо многочлен
- 11. Знайдемо коефіцієнти аі
- 13. Отримаємо многочлен Ньютона для
- 14. «Інтерполяція назад» використовується для знахо-дження значення функції
- 15. Оскільки k-ий
- 16. У формулі (*) коефіцієнтами многочлена є скінченні
- 18. Якщо коефіцієнти аі замінити на
- 19. Приклад 2. Дана таблиця значень теплоємності речовини
- 20. Скористаємось першою інтерполяцйною формулою, запишемо інтерполяційний многочлен
- 21. Кінець:)
Слайд 23.Нехай задана таблична функція:
Різниці І-го порядку або перші різниці визначаються формулами:
...
Різниці ІІ-го порядку або другі різниці визначаються формулами:
...
Різниці (n+1)-го порядку або (n+1) різниці визнача-ються формулами:
...
Слайд 4Приклад 1.
Кожне число цієї таблиці (починаючи з 3-го стовпчика) є різницею
двох сусідніх чисел стовпчика зліва = від нижнього числа віднімають верхнє,а різницю записують у наступному стовпчику між цими числами.
Слайд 13
Отримаємо многочлен Ньютона для рівномірної сітки
(*)
«Інтерполяція вперед» використовується для знаходження
значення функції f(x) у точці x, що розташована ближче до вузла x0
Слайд 14«Інтерполяція назад» використовується для знахо-дження значення функції f(x) у точці x,
що розташо-вана ближче до вузла xn
(**)
(**)
Слайд 15
Оскільки k-ий член многочлена Ньютона залежить тільки від k перших вузлів
інтерполяції і від значень функції у цих вузлах,то додавання нових вузлів призводить лише до додавання нових членів у формулі Ньютона без зміни попередніх
Слайд 16У формулі (*) коефіцієнтами многочлена є скінченні різниці, що знаходяться на
верхній бічній стороні рівнобедреного трикутника (одне підкреслення у таблиці різниць);
У формулі (**) коефіцієнтами многочлена є скінченні різниці, що знаходяться на нижній бічній стороні рівнобедреного трикутника (два підкреслення у таблиці різниць).
У формулі (**) коефіцієнтами многочлена є скінченні різниці, що знаходяться на нижній бічній стороні рівнобедреного трикутника (два підкреслення у таблиці різниць).
Слайд 18
Якщо коефіцієнти аі замінити на розділені різниці, то отримаємо многочлен Ньютона
для змінного кроку
Інтерполяційна формула Ньютона:
Інтерполяційна формула Ньютона:
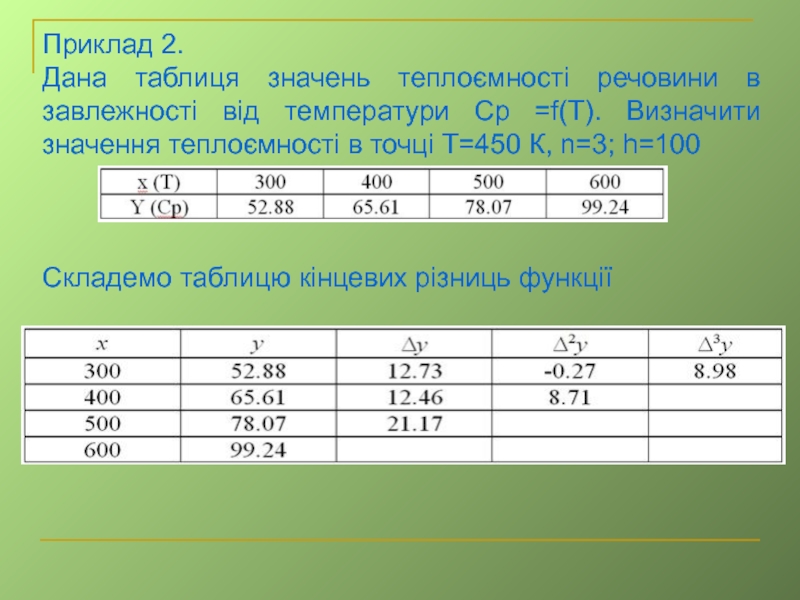
Слайд 19Приклад 2.
Дана таблиця значень теплоємності речовини в завлежності від температури Cр
=f(T). Визначити значення теплоємності в точці Т=450 К, n=3; h=100
Складемо таблицю кінцевих різниць функції
Складемо таблицю кінцевих різниць функції
Слайд 20Скористаємось першою інтерполяцйною формулою, запишемо інтерполяційний многочлен при x=450 К.
Таким чином,
теплоємність при температурі 450 К буде: Сp(450)=71,31Дж/(моль*К).