- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие квадратного корня из неотрицательного числа презентация
Содержание
- 1. Понятие квадратного корня из неотрицательного числа
- 2. Понятие квадратного корня из неотрицательного числа Рассмотрим
- 3. Понятие квадратного корня из неотрицательного числа Рассмотрим
- 4. Понятие квадратного корня из неотрицательного числа Оказывается
- 5. Понятие квадратного корня из неотрицательного числа Итак
- 6. Понятие квадратного корня из неотрицательного числа Определение:
- 7. Понятие квадратного корня из неотрицательного числа Равенство
- 8. Понятие квадратного корня из неотрицательного числа Примеры:
- 9. Домашнее задание Сделать конспект параграфа 9( красный
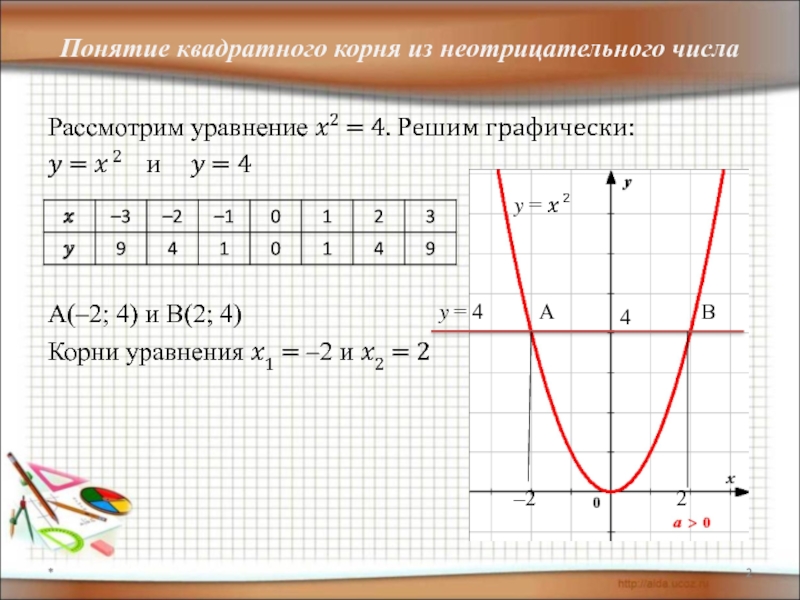
Слайд 2Понятие квадратного корня из неотрицательного числа
Рассмотрим уравнение ?2 = 4. Решим
? = ? 2 и ? = 4
А(–2; 4) и В(2; 4)
Корни уравнения ?1 = –2 и ?2 = 2
*
4
–2
2
А
В
? = 4
? = ? 2
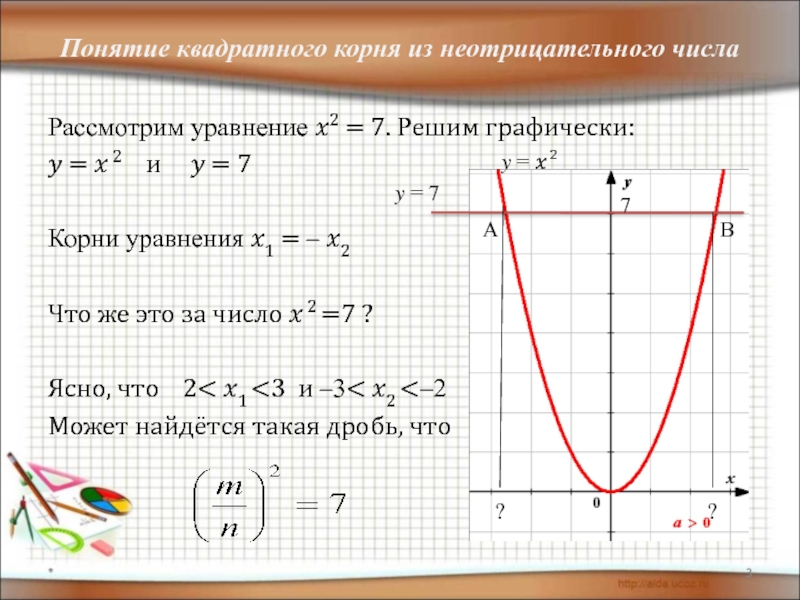
Слайд 3Понятие квадратного корня из неотрицательного числа
Рассмотрим уравнение ?2 = 7. Решим
? = ? 2 и ? = 7
Корни уравнения ?1 = – ?2
Что же это за число ? 2 =7 ?
Ясно, что 2< ?1 <3 и –3< ?2 <–2
Может найдётся такая дробь, что
*
7
А
В
? = 7
? = ? 2
?
?
Слайд 4Понятие квадратного корня из неотрицательного числа
Оказывается такой дроби нет! (смотри доказательство
Встретившись с подобной ситуацией, математики поняли, что надо придумать способ её описания на математическом языке.
Они ввели в рассмотрение новый символ и с его помощью корни уравнения ?2 = 7 записали так:
?1 = ?2 = –
*
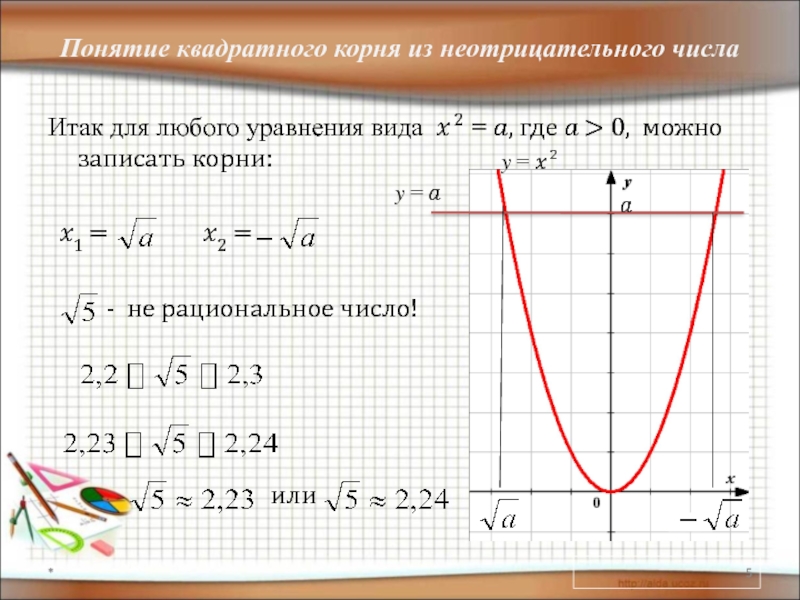
Слайд 5Понятие квадратного корня из неотрицательного числа
Итак для любого уравнения вида ?
?1 = ?2 =
- не рациональное число!
или
*
?
? = ?
? = ? 2
Слайд 6Понятие квадратного корня из неотрицательного числа
Определение: Квадратным корнем из неотрицательного числа
, где ? – называют подкоренным числом
Итак, если ? – неотрицательное число, то:
1)
2)
Если ? < 0, то уравнение ?2 = ? не имеет корней
Если ? = 0, то уравнение ?2 = ? имеет один корень ?1= 0
Если ? > 0, то уравнение ?2 = ? имеет два корня
?1 = ?2 =
*
Слайд 7Понятие квадратного корня из неотрицательного числа
Равенство
Операцию по нахождению квадратного корня из неотрицательного числа называют извлечением квадратного корня.
Эта операция является обратной по отношению к возведению в квадрат.
*
Слайд 8Понятие квадратного корня из неотрицательного числа
Примеры:
= 15 , так как 15>0 и 152 = 225
= 9 , так как 9>0 и 92 = 81
= , так как >0 и =
= 31 , так как 31>0 и 312 = 961
= не существует!
≈ 3,16
*
Слайд 9Домашнее задание
Сделать конспект параграфа 9( красный учебник стр. 35-40 с примерами)
Определение
Прочитать параграф 10 (стр. 42-43)
*