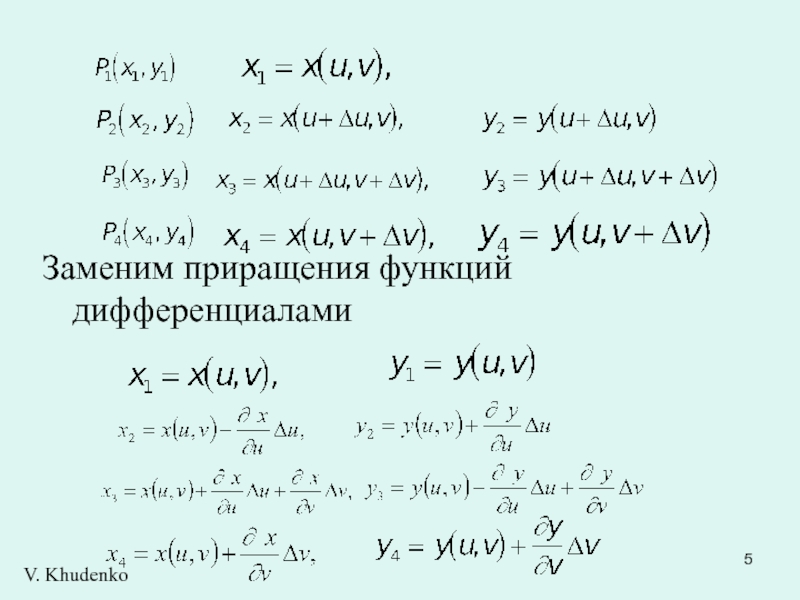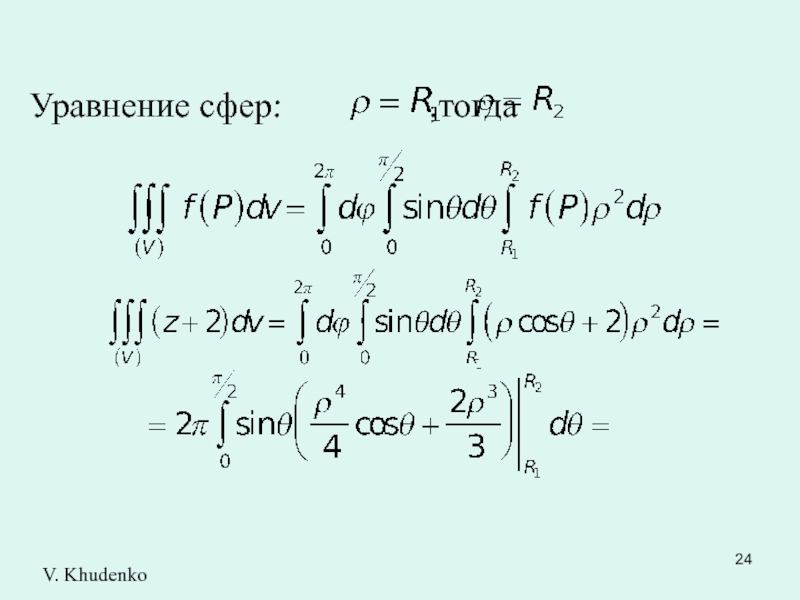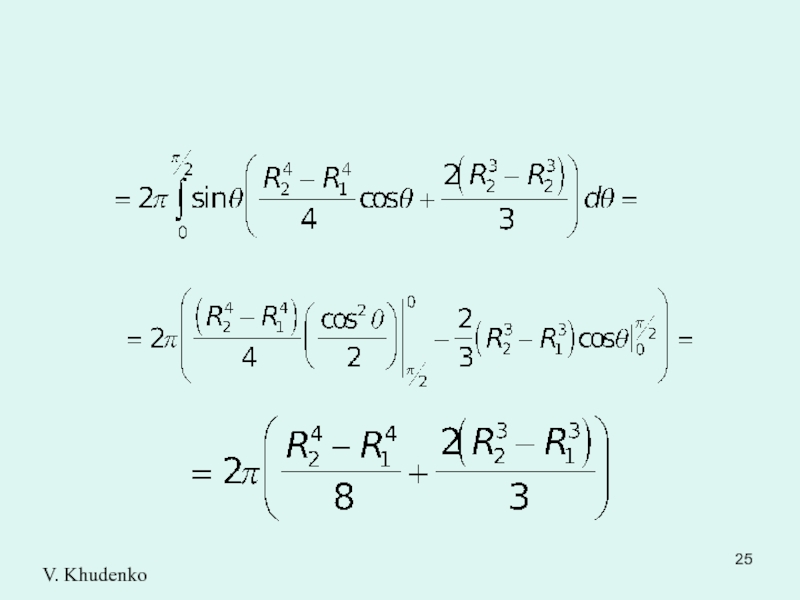случай замены переменной в двойном и тройном интегралах
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Замена переменных в интеграле по фигуре от скалярной функции презентация
Содержание
- 1. Замена переменных в интеграле по фигуре от скалярной функции
- 2. Замена переменных в двойном интеграле Пусть
- 3. V. Khudenko
- 4. Разобьем область
- 6. Полученные выражения дают основание считать
- 7. Введем обозначение Определитель
- 8. Замечание Переход к полярным координатам в
- 9. Вычисление тройного интеграла в цилиндрических координатах
- 10. В случае перехода к цилиндрическим
- 11. а формула замены переменных при
- 13. Таким образом интеграл, после расстановки пределов интегрирования запишется в виде V. Khudenko
- 14. Пример Расставить пределы интегрирования в тройном
- 17. Следовательно, область (V) задана неравенствами:
- 18. Вычисление тройного интеграла в сферических координатах
- 19. формула замены переменных применительно к сферическим координатам примет вид V. Khudenko
- 21. Получаем формулу V. Khudenko
- 22. Пример Расставить пределы интегрирования в тройном
- 24. Уравнение сфер: ,тогда V. Khudenko
- 25. V. Khudenko
Замена переменных в двойном интеграле Пусть в плоскости Оху задана область (D), ограниченная линией (L). Предположим, что осуществляется замена переменных (*) причем функции x=x(u,v), y=y(u,v) взаимно однозначны и дифференцируемы в
Слайд 2 Замена переменных в двойном интеграле
Пусть в плоскости Оху задана область
(D), ограниченная линией (L). Предположим, что осуществляется замена переменных
(*)
причем функции x=x(u,v), y=y(u,v) взаимно однозначны и дифференцируемы в области (D).
Формулы (*) устанавливают взаимно однозначное соответствие между точками (x,y)∈D и
(*)
причем функции x=x(u,v), y=y(u,v) взаимно однозначны и дифференцируемы в области (D).
Формулы (*) устанавливают взаимно однозначное соответствие между точками (x,y)∈D и
V. Khudenko
Слайд 4
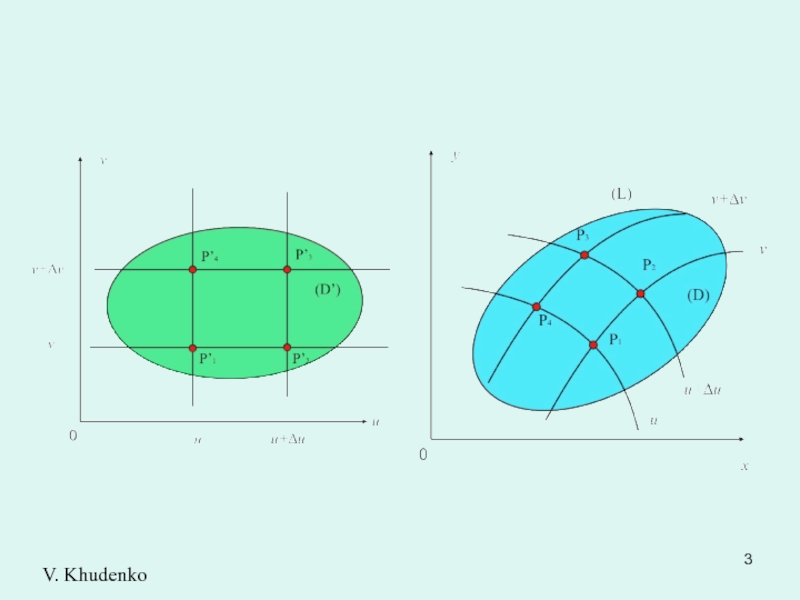
Разобьем область прямыми
,
на прямоугольные площадки.
Тогда область (D) соответствующими кривыми линиями разобьется на криволинейные четырехугольники . Площадь элементарной фигуры
на плоскости Найдем площадь соответствующей ей фигуры P1P2P3P4 достаточно малого четырехугольника координаты вершин которого
на прямоугольные площадки.
Тогда область (D) соответствующими кривыми линиями разобьется на криволинейные четырехугольники . Площадь элементарной фигуры
на плоскости Найдем площадь соответствующей ей фигуры P1P2P3P4 достаточно малого четырехугольника координаты вершин которого
V. Khudenko
Слайд 6
Полученные выражения дают основание считать четырехугольник параллелограммом со сторонами
V. Khudenko
Слайд 7
Введем обозначение
Определитель I называется функциональным определителем функций
и или якобианом .
Имеет место равенство:
Тогда формула замены переменных для двойного интеграла примет вид
Имеет место равенство:
Тогда формула замены переменных для двойного интеграла примет вид
V. Khudenko
Слайд 8Замечание
Переход к полярным координатам в двойном интеграле является частным случаем
при u=r и v=φ. Тогда
V. Khudenko
Слайд 9 Вычисление тройного интеграла в цилиндрических координатах
Якобиан для случая трех переменных
Формула
замены переменных для тройного интеграла примет вид
V. Khudenko
Слайд 10
В случае перехода к цилиндрическим координатам
связь между декартовыми и цилиндрическими
координатами:
Тогда определитель Якоби
Тогда определитель Якоби
V. Khudenko
Слайд 11
а формула замены переменных при переходе к цилиндрическим координатам примет
вид
V. Khudenko
Слайд 13
Таким образом интеграл, после расстановки пределов интегрирования запишется в виде
V. Khudenko
Слайд 14Пример
Расставить пределы интегрирования в тройном интеграле
и вычислить его значение в случае
Область ограничена поверхностями:
Учтем характер области:
V. Khudenko
Слайд 18Вычисление тройного интеграла в сферических координатах
Положим u=ρ, v=φ, w=θ.
Зависимость между декартовыми и сферическими координатами
определитель Якоби
определитель Якоби
V. Khudenko
Слайд 22Пример
Расставить пределы интегрирования в тройном интеграле, если область (V) представляет
собой часть пространства. Ограниченную поверхностями
Причем а также вычислить
Причем а также вычислить
V. Khudenko
