- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей презентация
Содержание
- 1. Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей
- 2. 5.1. Параллельность прямой и плоскости; двух
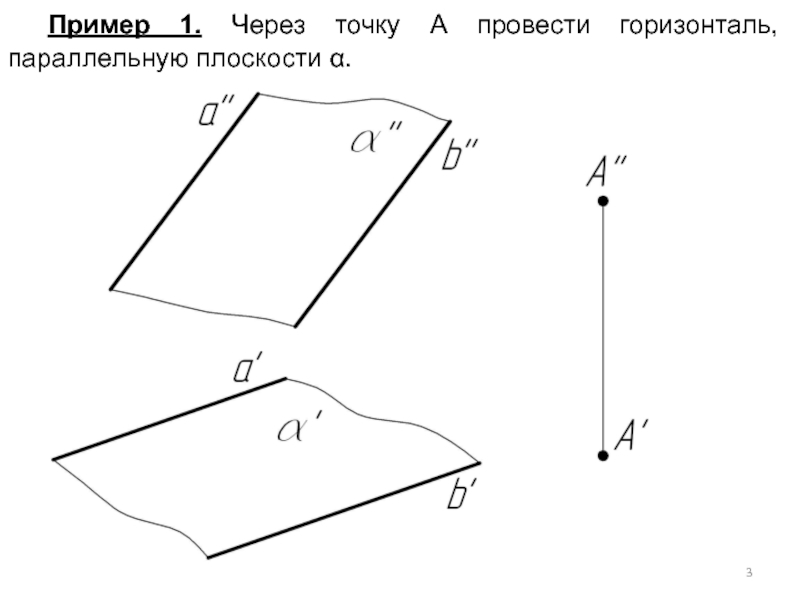
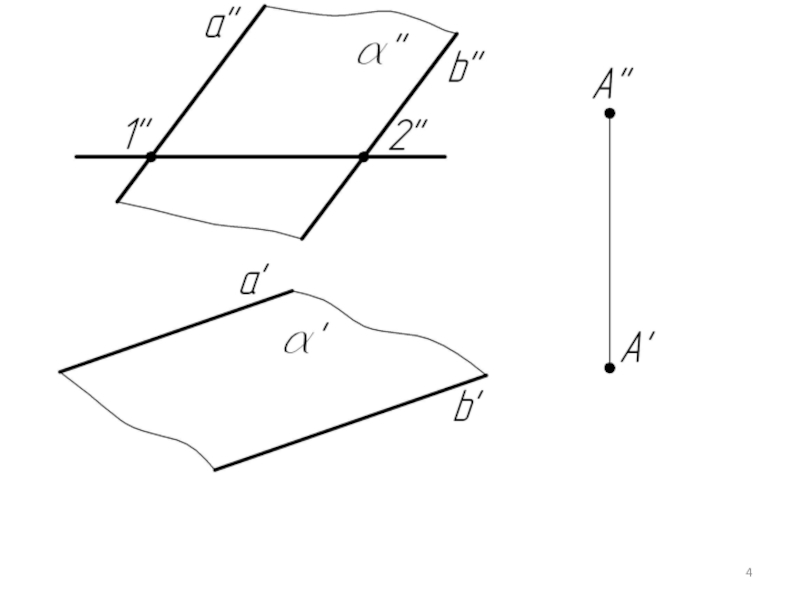
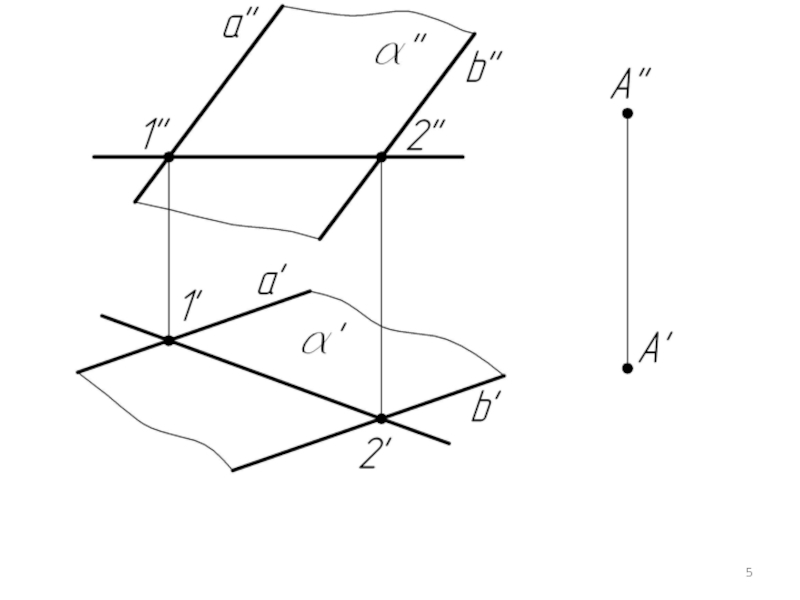
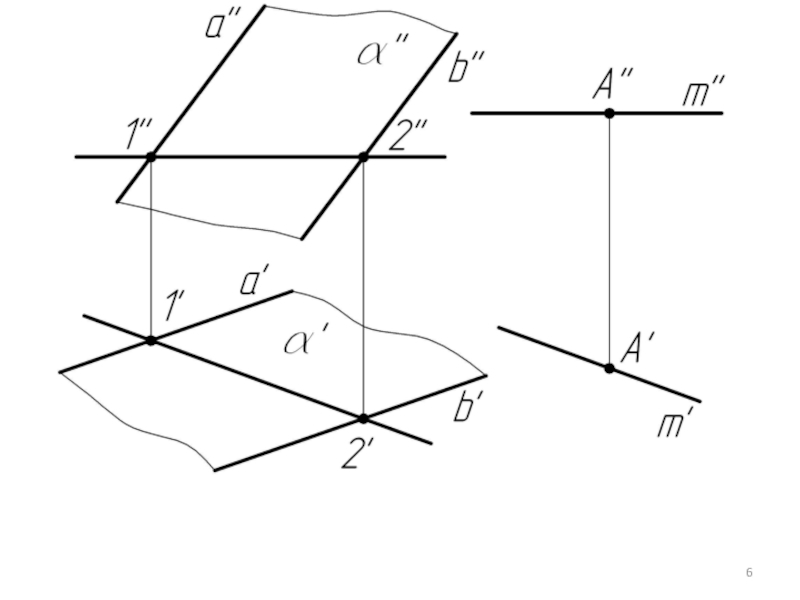
- 3. Пример 1. Через точку А провести горизонталь, параллельную плоскости α.
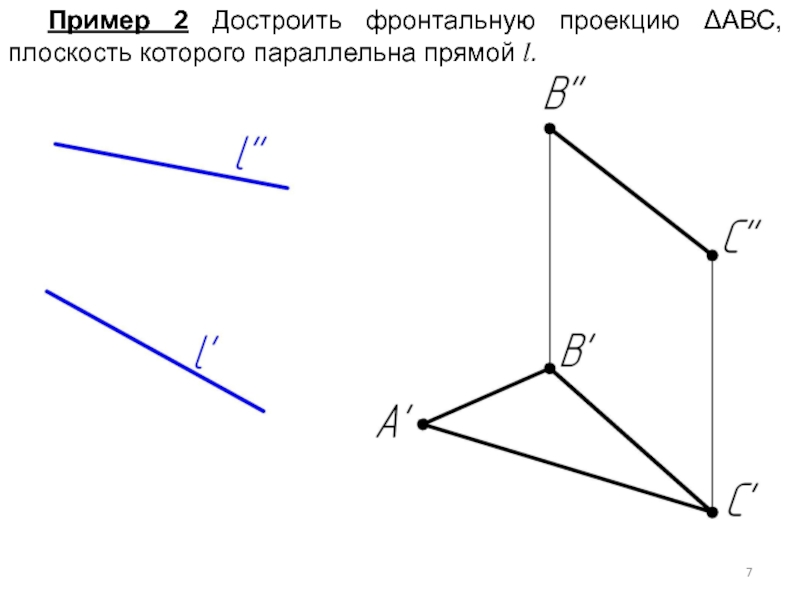
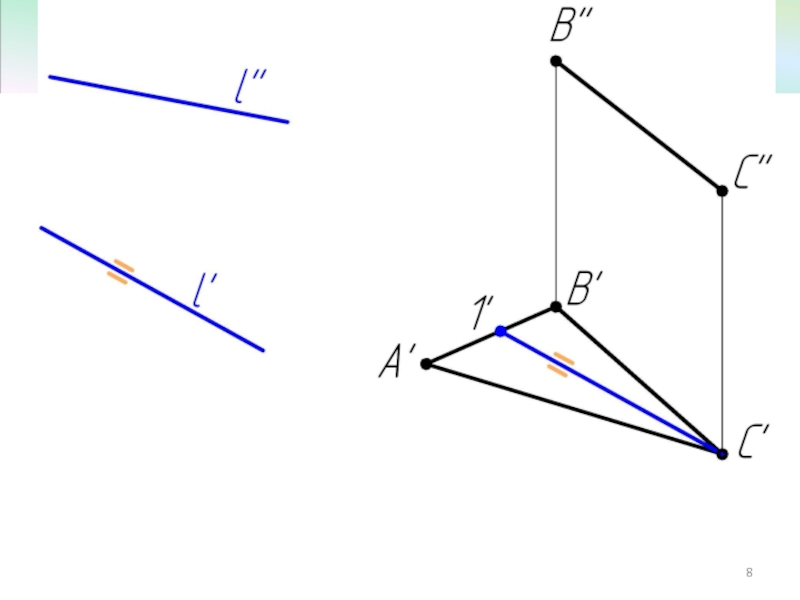
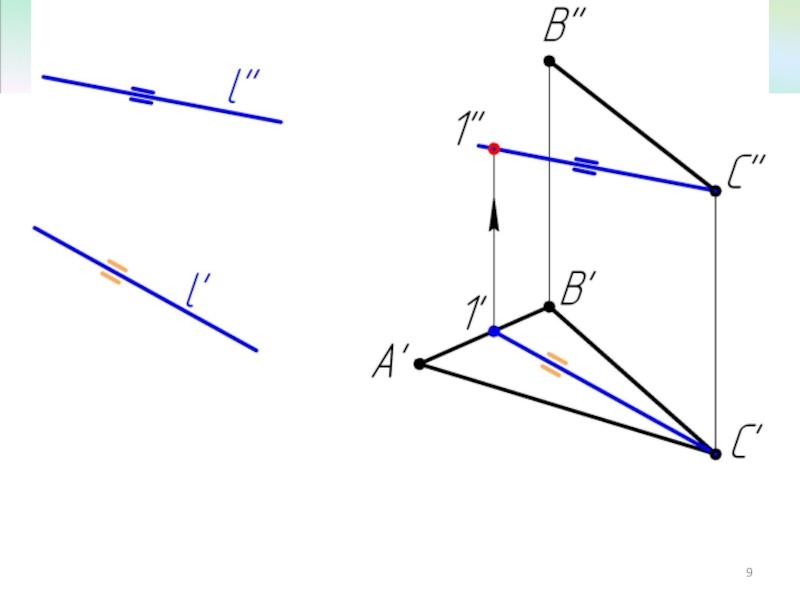
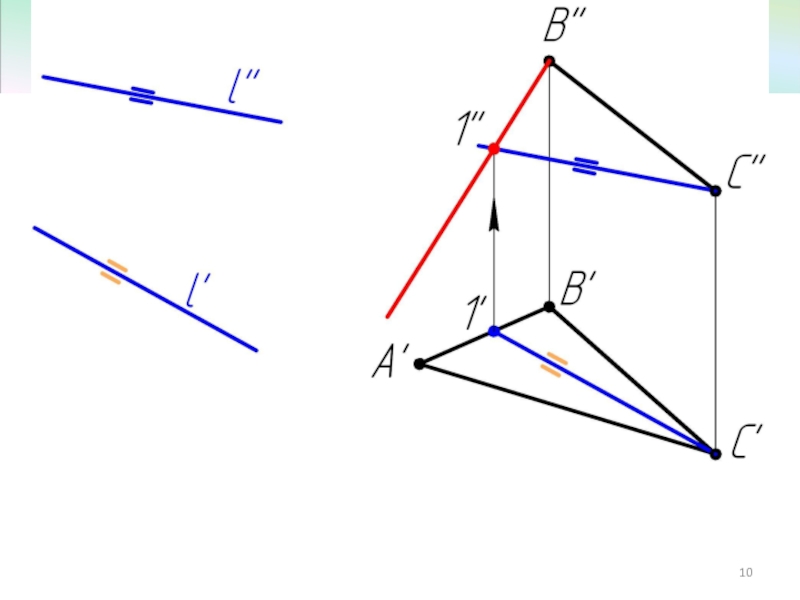
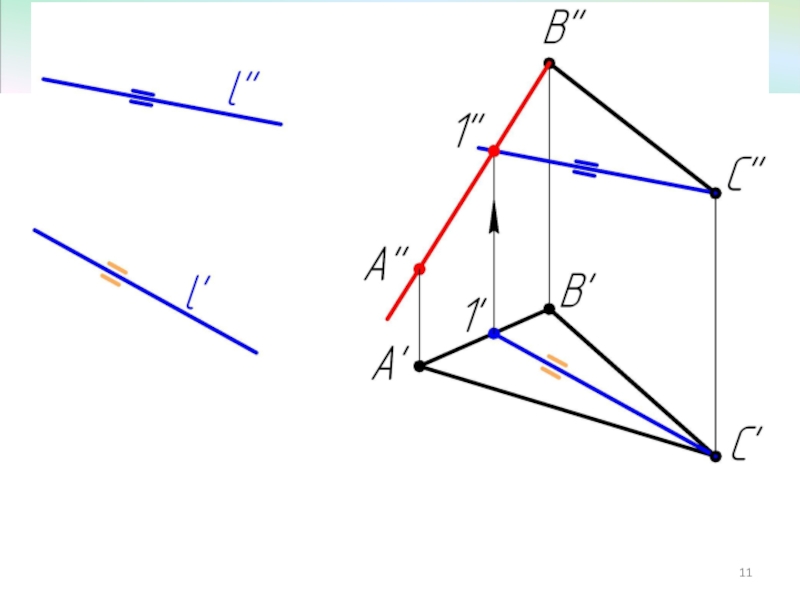
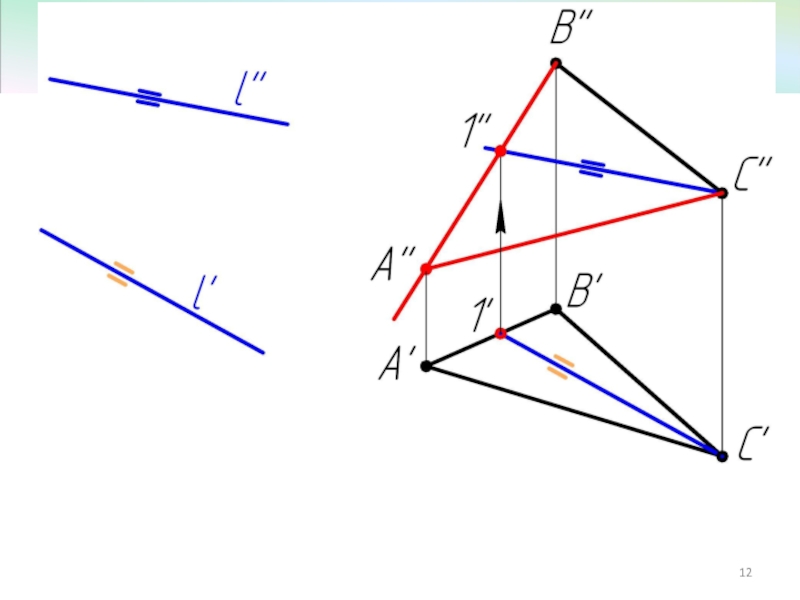
- 7. Пример 2 Достроить фронтальную проекцию ΔАВС, плоскость которого параллельна прямой l.
- 13. Две плоскости параллельны, если две пересекающиеся прямые
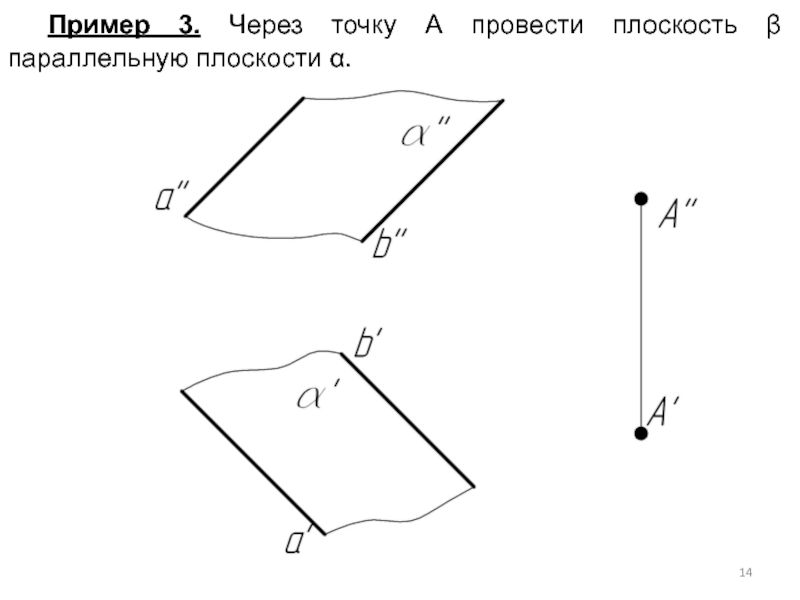
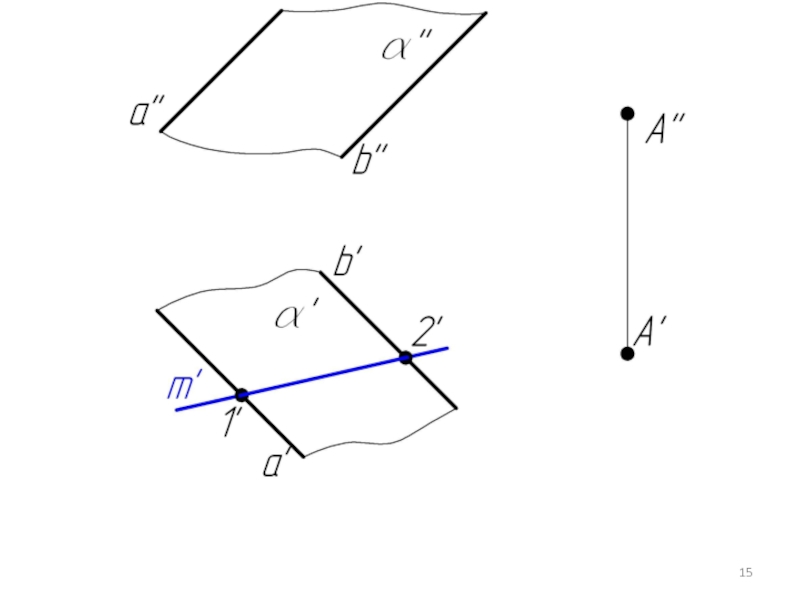
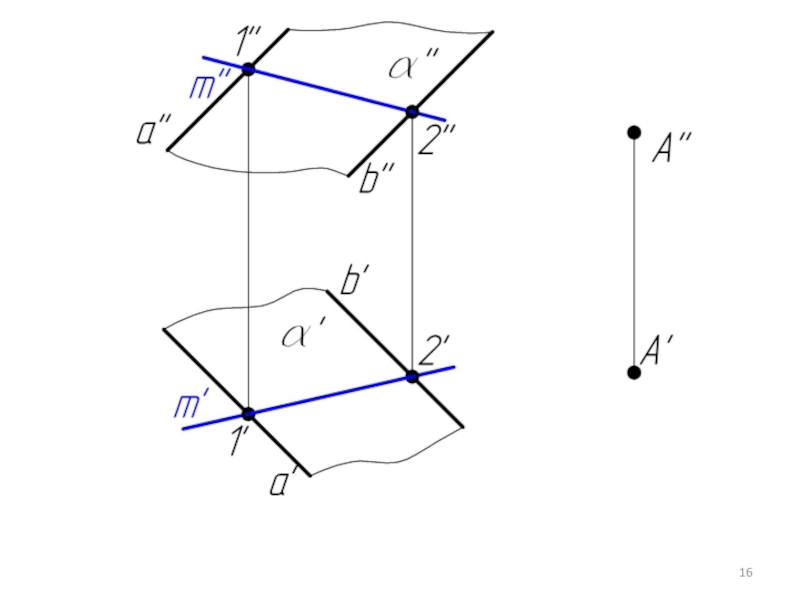
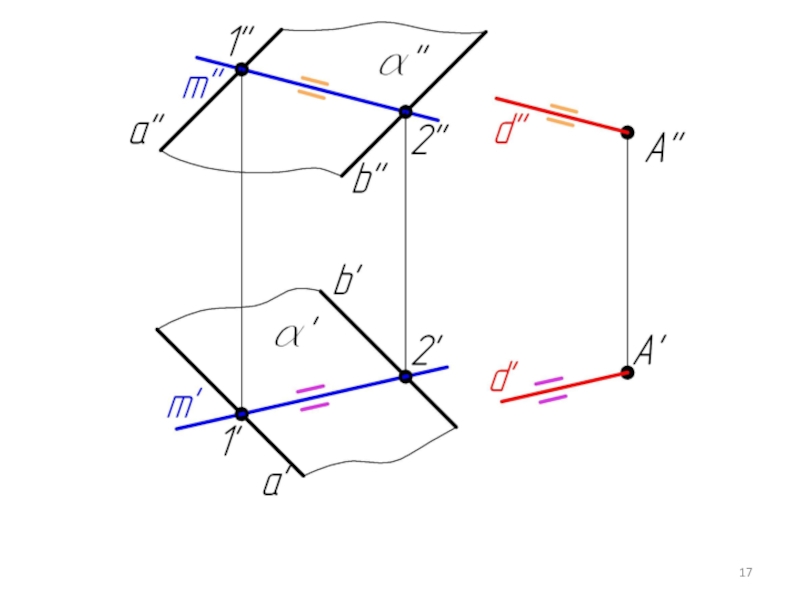
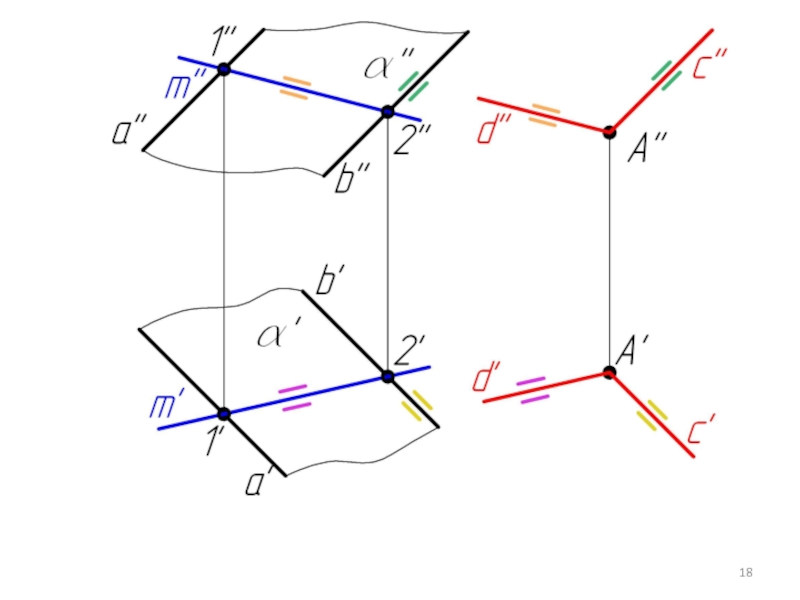
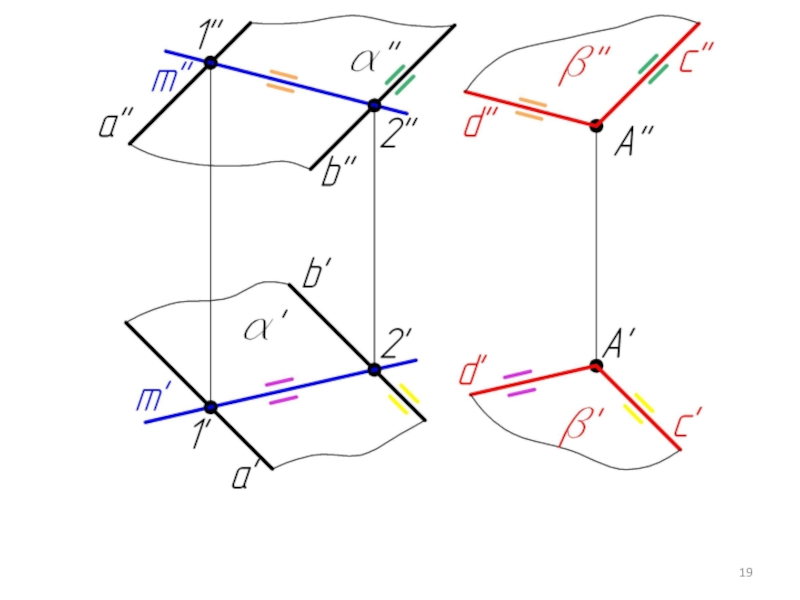
- 14. Пример 3. Через точку А провести плоскость β параллельную плоскости α.
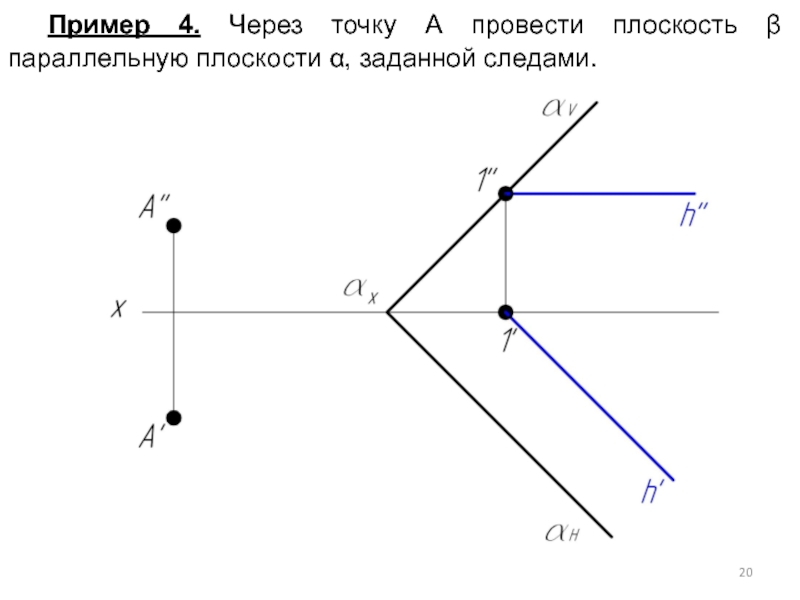
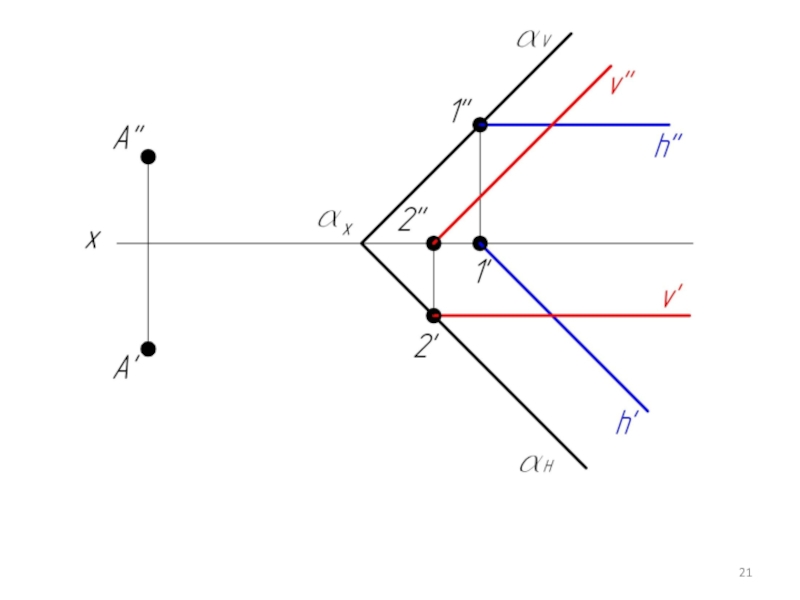
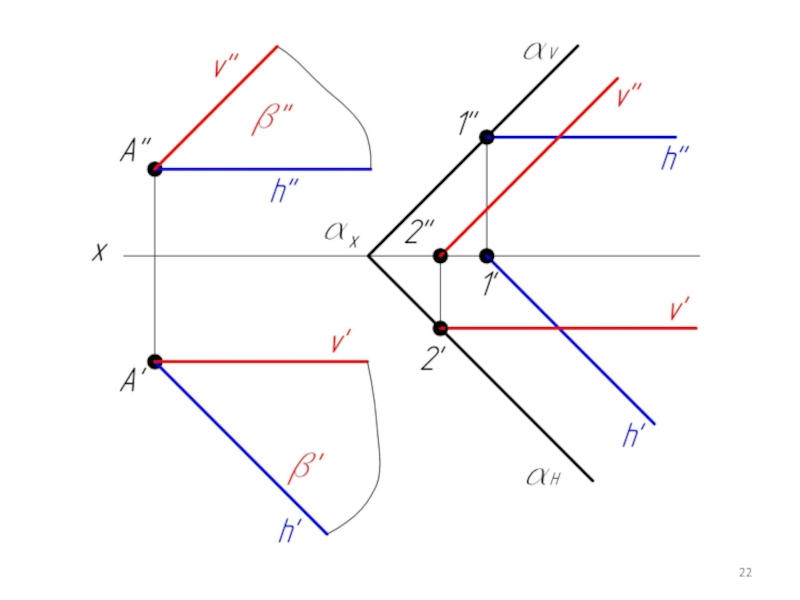
- 20. Пример 4. Через точку А провести плоскость β параллельную плоскости α, заданной следами.
- 23. Позиционные задачи Позиционные задачи – это задачи
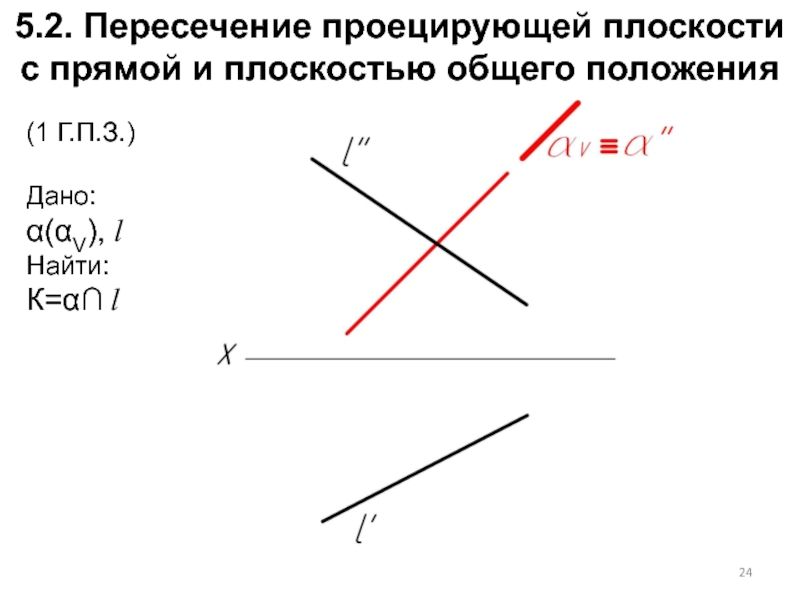
- 24. 5.2. Пересечение проецирующей плоскости с прямой и
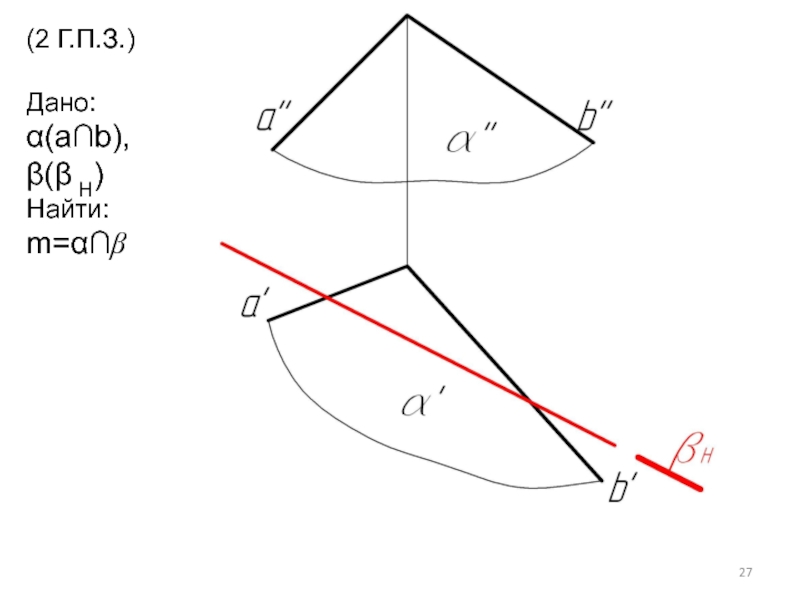
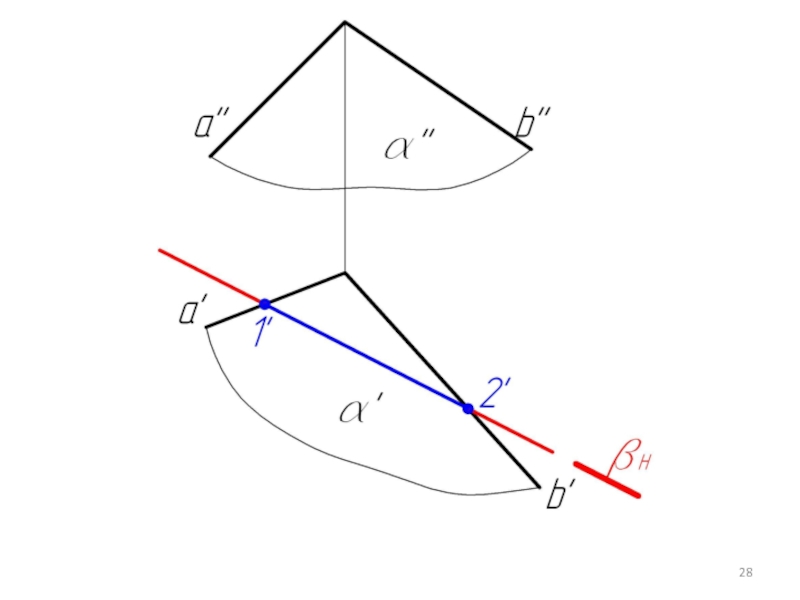
- 27. (2 Г.П.З.) Дано: α(а∩b), β(β Н) Найти: m=α∩β
- 30. Если один из геометрических образов при пересечении
- 31. 5.3. Построение линий пересечения двух плоскостей в
- 32. Две плоскости пересекаются по прямой . Для
- 41. 5.4. Построение линий пересечения двух плоскостей заданных
- 42. В частных случаях направление линии пересечения известно,
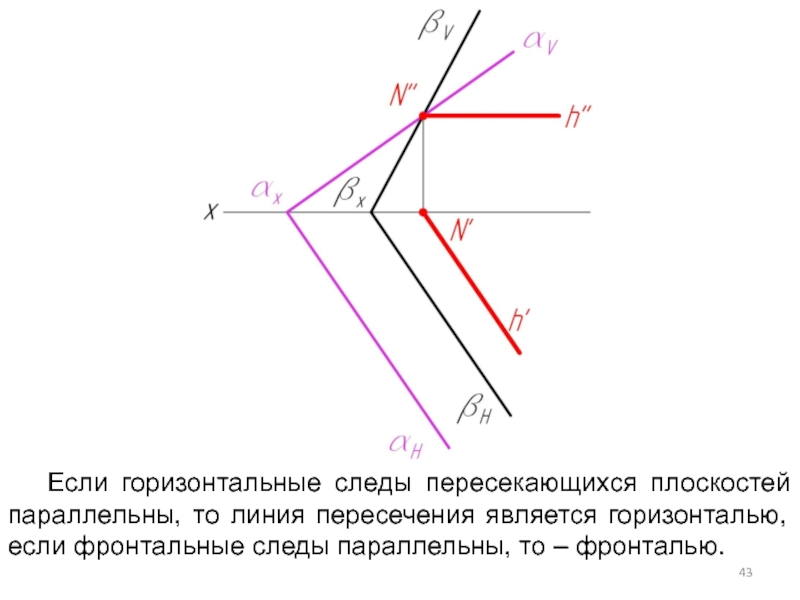
- 43. Если горизонтальные следы пересекающихся плоскостей параллельны, то
- 44. 5.5. Пересечение прямой с плоскостью в общем
- 54. D(130, 65, 30) E (90,
5.1. Параллельность прямой и плоскости; двух плоскостей. Прямая параллельна плоскости, если она параллельна прямой, принадлежащей плоскости. Плоскость параллельна прямой, если она проходит через прямую параллельную данной прямой.
Слайд 2 5.1. Параллельность прямой и плоскости; двух плоскостей.
Прямая параллельна плоскости,
если она параллельна прямой, принадлежащей плоскости.
Плоскость параллельна прямой, если она проходит через прямую параллельную данной прямой.
Плоскость параллельна прямой, если она проходит через прямую параллельную данной прямой.
Слайд 13Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости.
Если плоскости заданы следами, то одноименные следы параллельных плоскостей параллельны.
Если плоскости заданы следами, то одноименные следы параллельных плоскостей параллельны.
Слайд 23Позиционные задачи
Позиционные задачи – это задачи на взаимное расположение геометрических фигур.
1 главная позиционная задача (1 Г.П.З.) – это задача на пересечение линии и поверхности (в частном случае линии и плоскости).
2 главная позиционная задача (2 Г.П.З.) - это задача на пересечение поверхностей (в частном случае плоскостей).
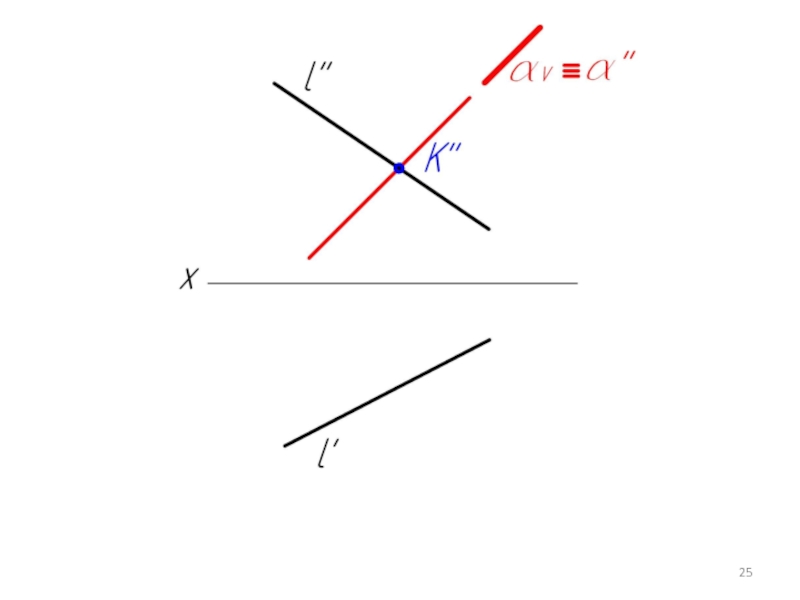
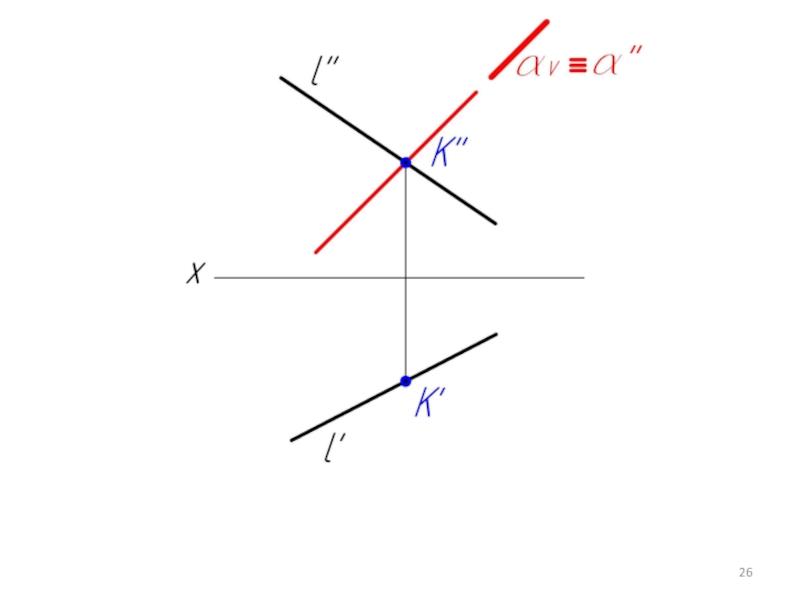
Слайд 245.2. Пересечение проецирующей плоскости с прямой и плоскостью общего положения
(1 Г.П.З.)
Дано:
α(αV),
l
Найти:
К=α∩ l
Найти:
К=α∩ l
Слайд 30Если один из геометрических образов при пересечении занимает частное положение (в
первом случае плоскость α - фронтально-проецирующая, во втором - β - горизонтально-проецирующая), то точка или линия пересечения уже есть на чертеже.
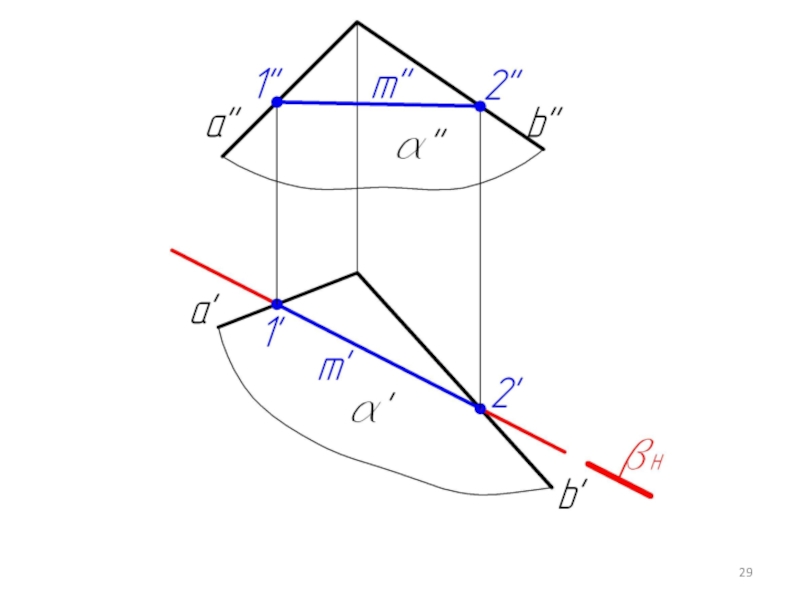
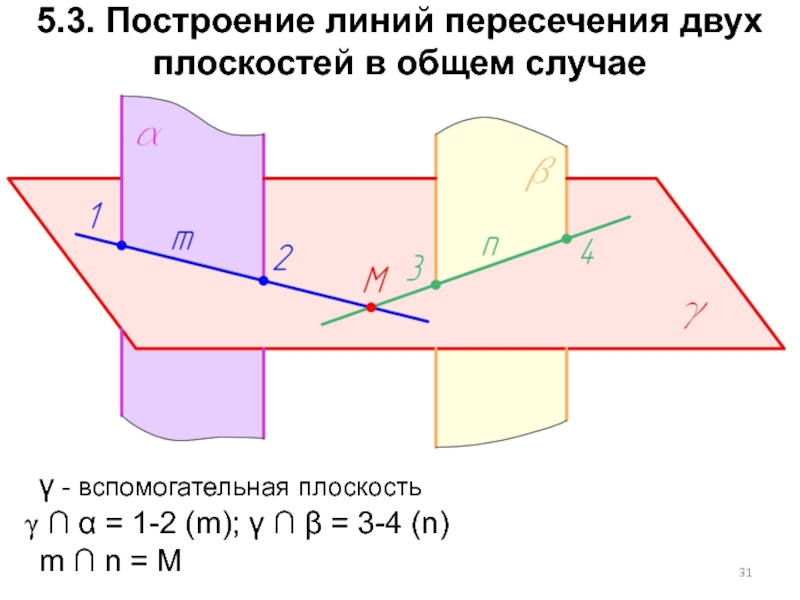
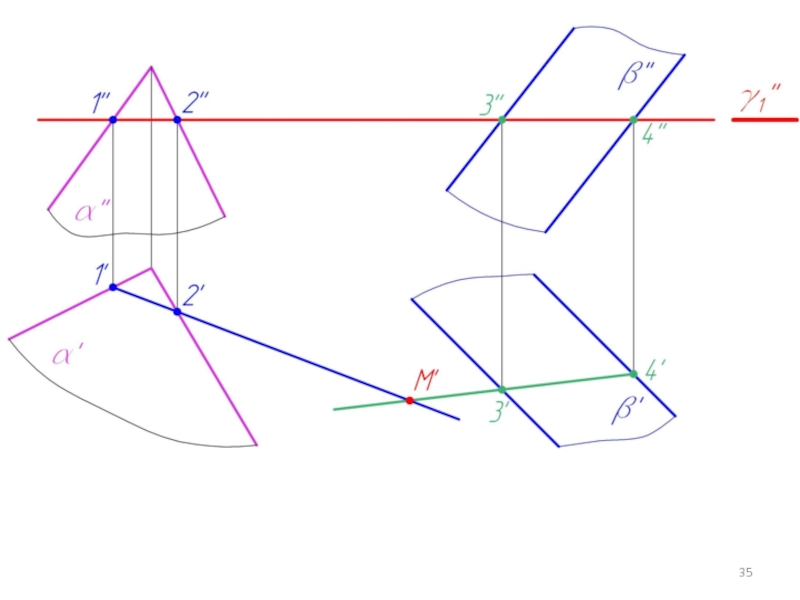
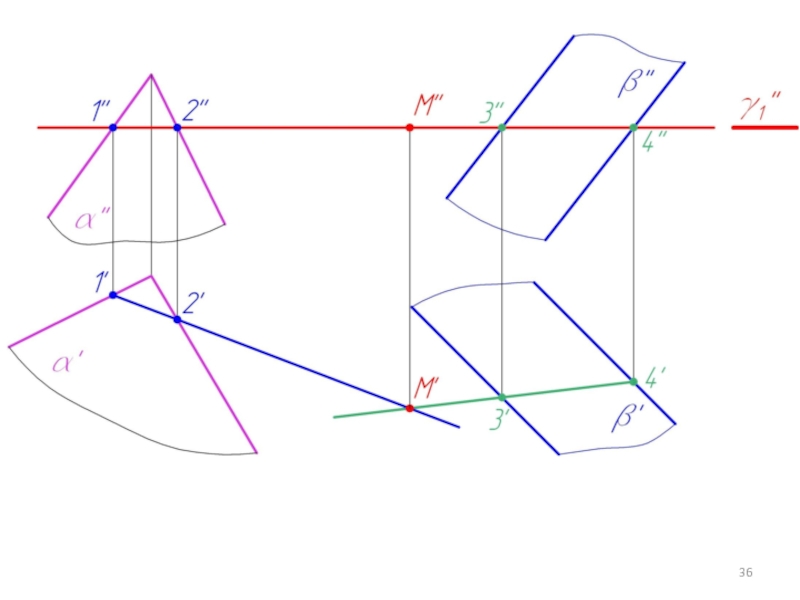
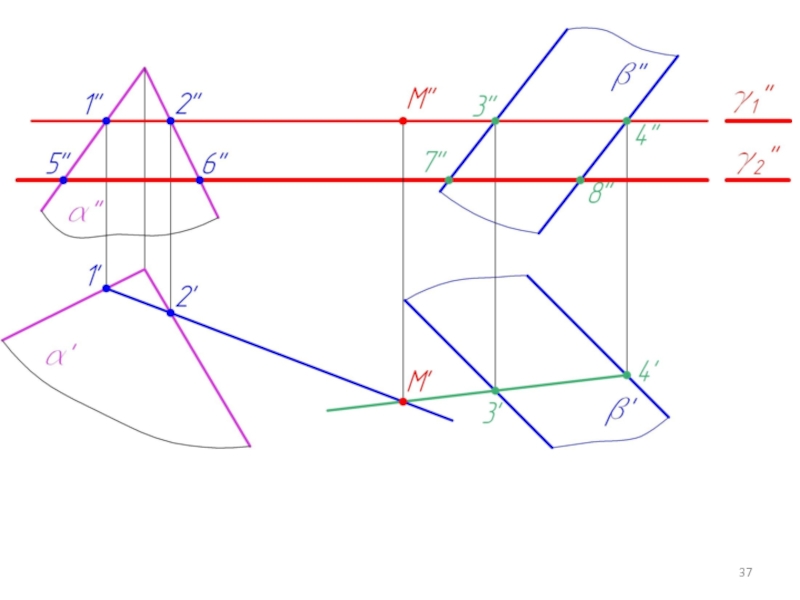
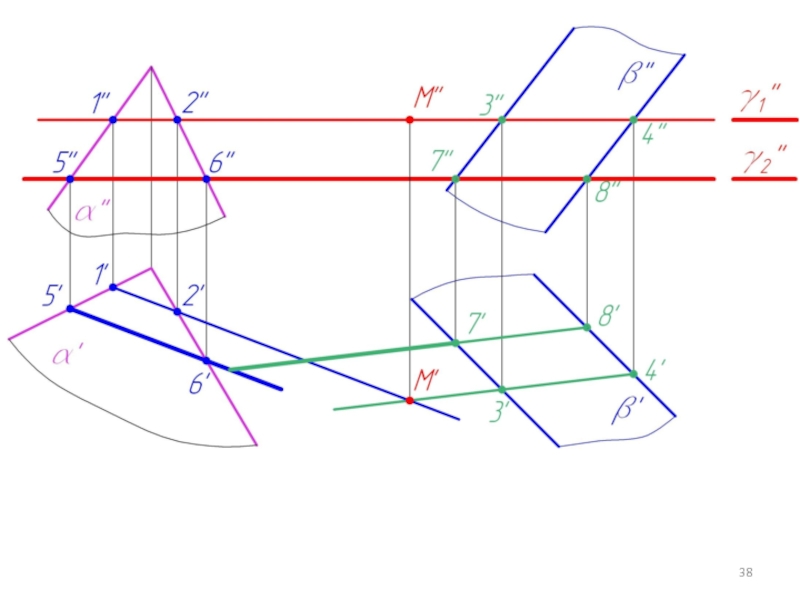
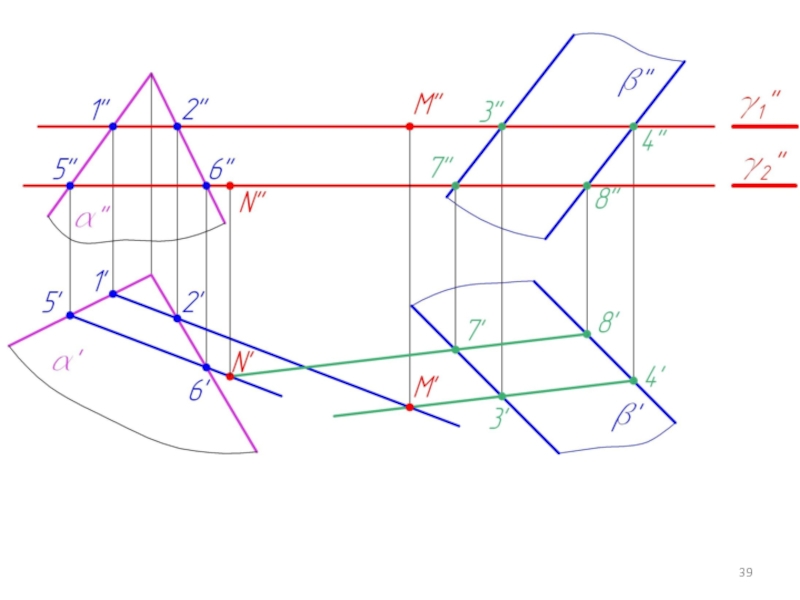
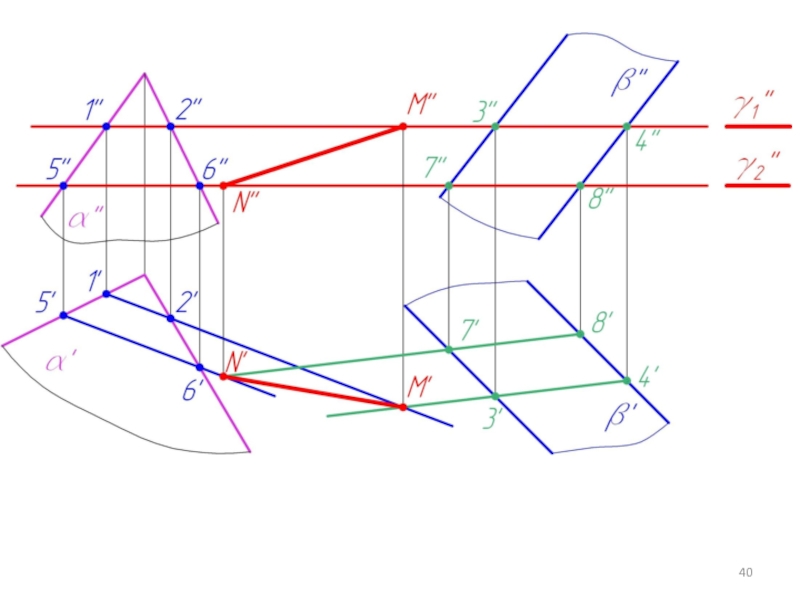
Слайд 315.3. Построение линий пересечения двух плоскостей в общем случае
γ - вспомогательная
плоскость
∩ α = 1-2 (m); γ ∩ β = 3-4 (n)
m ∩ n = M
∩ α = 1-2 (m); γ ∩ β = 3-4 (n)
m ∩ n = M
Слайд 32Две плоскости пересекаются по прямой .
Для ее построения нужно найти две
точки, общие для двух заданных плоскостей α и β.
Чтобы построить такую точку, нужно:
1. Пересечь заданные плоскости α и β вспомогательной плоскостью γ;
2. Построить линии пересечения плоскостей α и β с плоскостью γ;
3. Найти точку пересечения этих линий m ∩ n = M
Чтобы построить такую точку, нужно:
1. Пересечь заданные плоскости α и β вспомогательной плоскостью γ;
2. Построить линии пересечения плоскостей α и β с плоскостью γ;
3. Найти точку пересечения этих линий m ∩ n = M
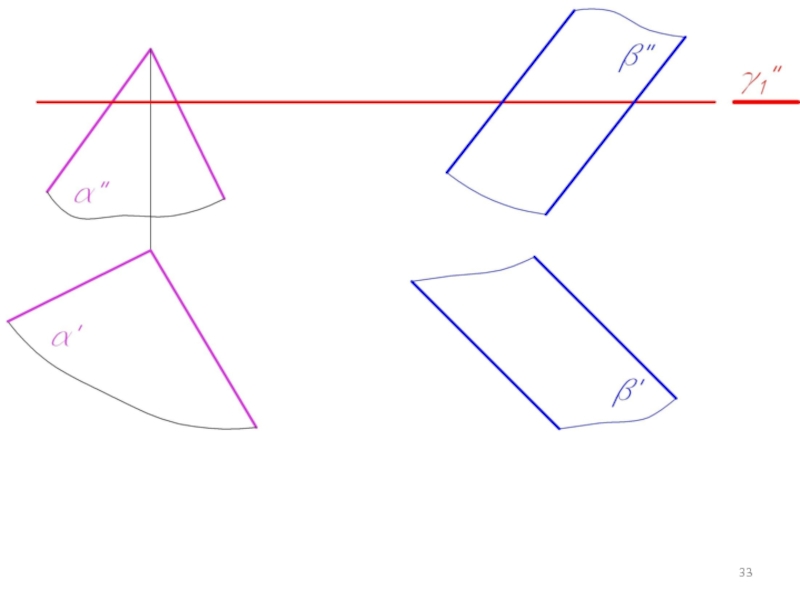
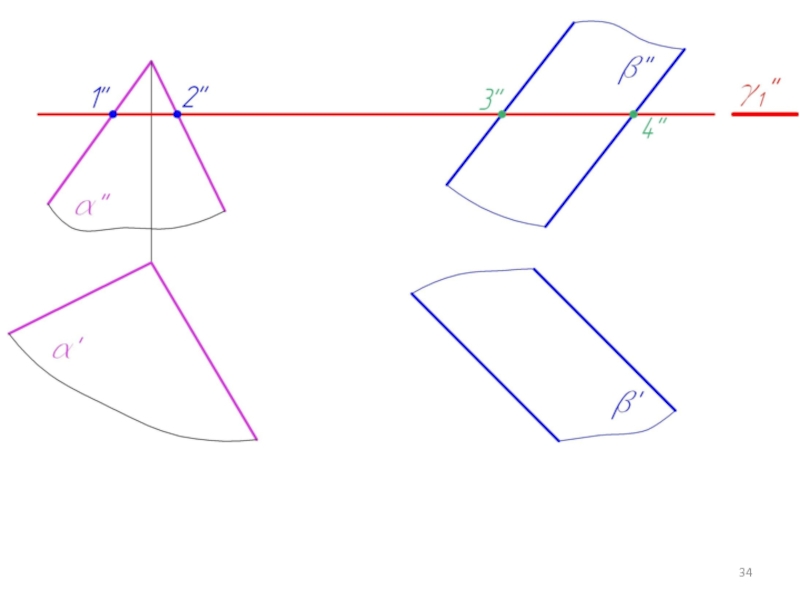
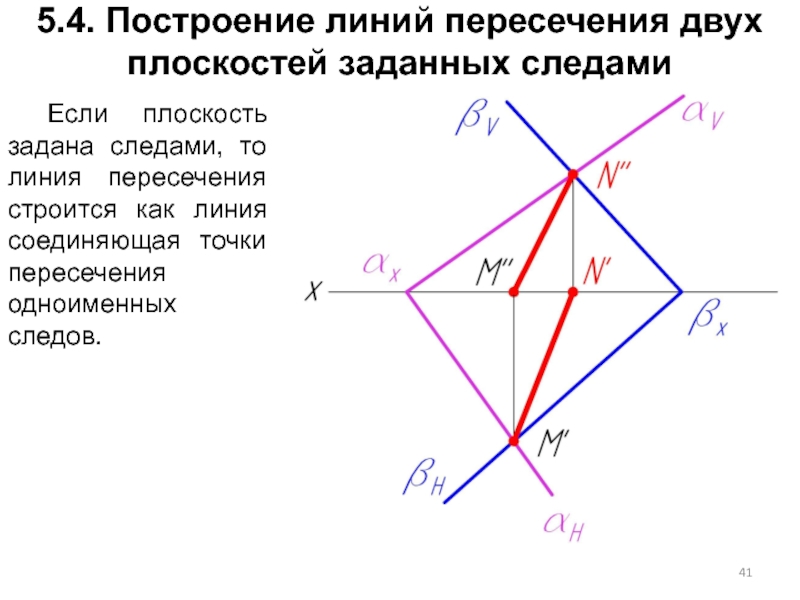
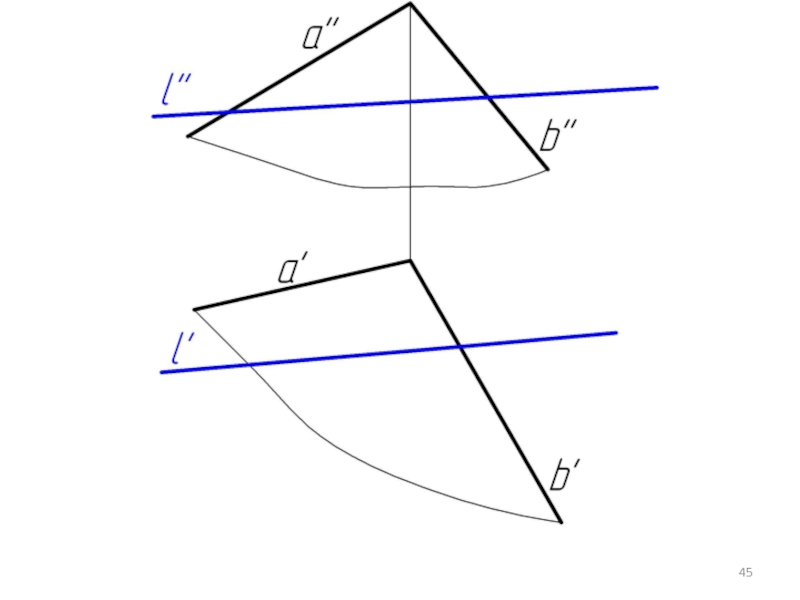
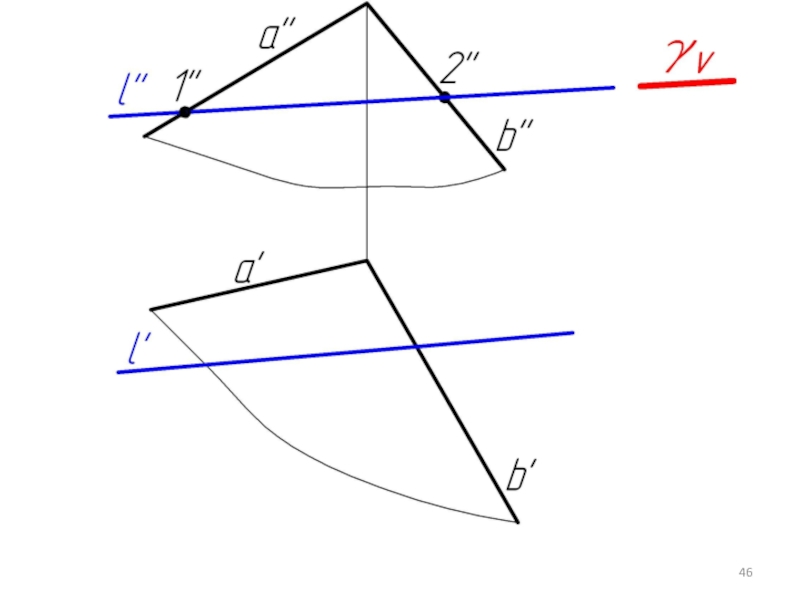
Слайд 415.4. Построение линий пересечения двух плоскостей заданных следами
Если плоскость задана следами,
то линия пересечения строится как линия соединяющая точки пересечения одноименных следов.
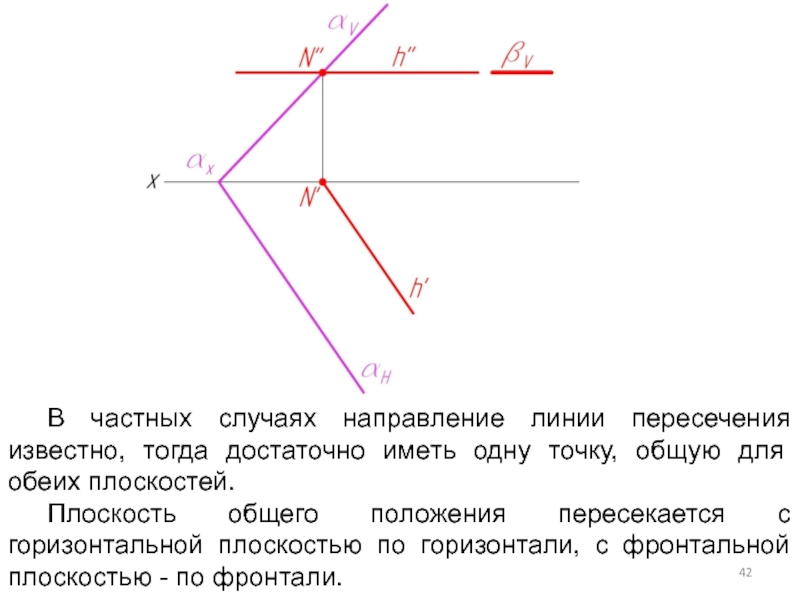
Слайд 42В частных случаях направление линии пересечения известно, тогда достаточно иметь одну
точку, общую для обеих плоскостей.
Плоскость общего положения пересекается с горизонтальной плоскостью по горизонтали, с фронтальной плоскостью - по фронтали.
Плоскость общего положения пересекается с горизонтальной плоскостью по горизонтали, с фронтальной плоскостью - по фронтали.
Слайд 43Если горизонтальные следы пересекающихся плоскостей параллельны, то линия пересечения является горизонталью,
если фронтальные следы параллельны, то – фронталью.
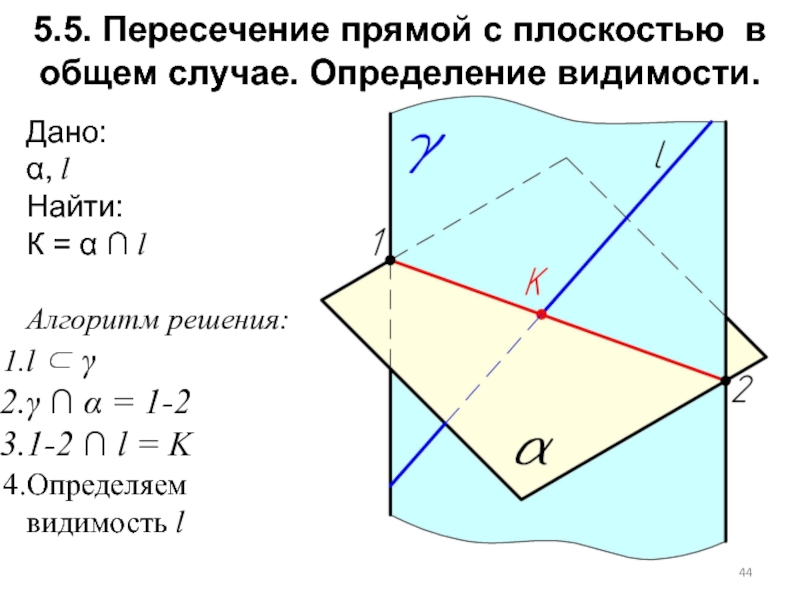
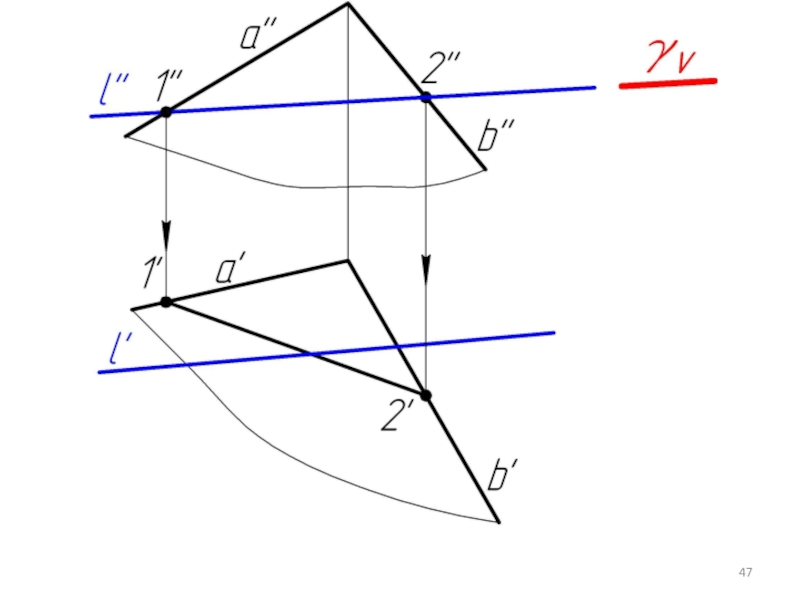
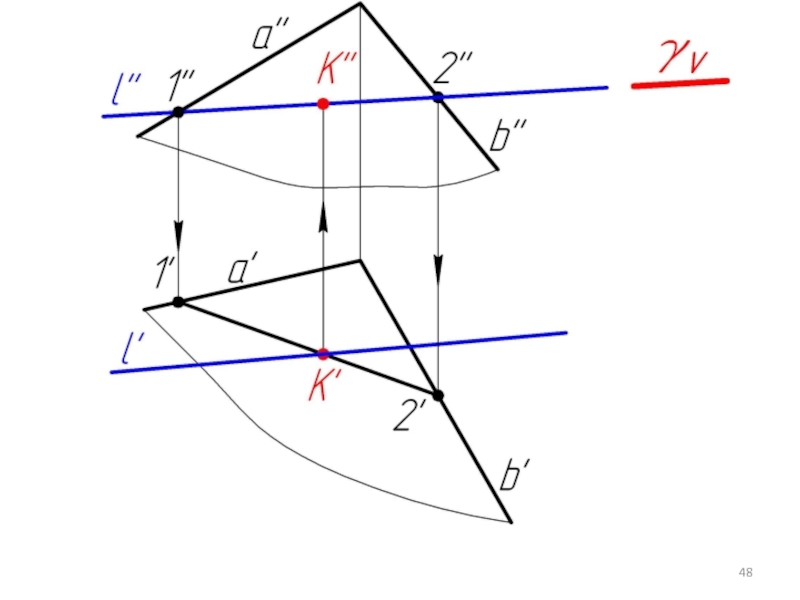
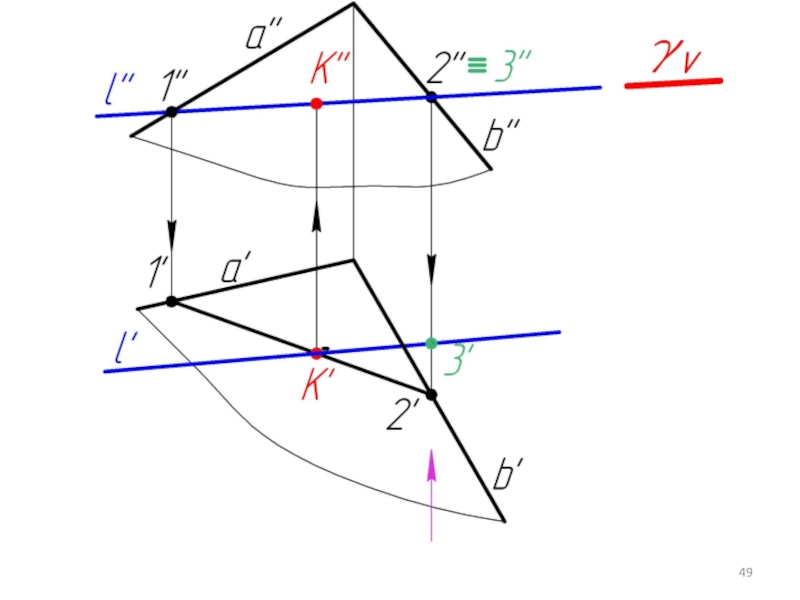
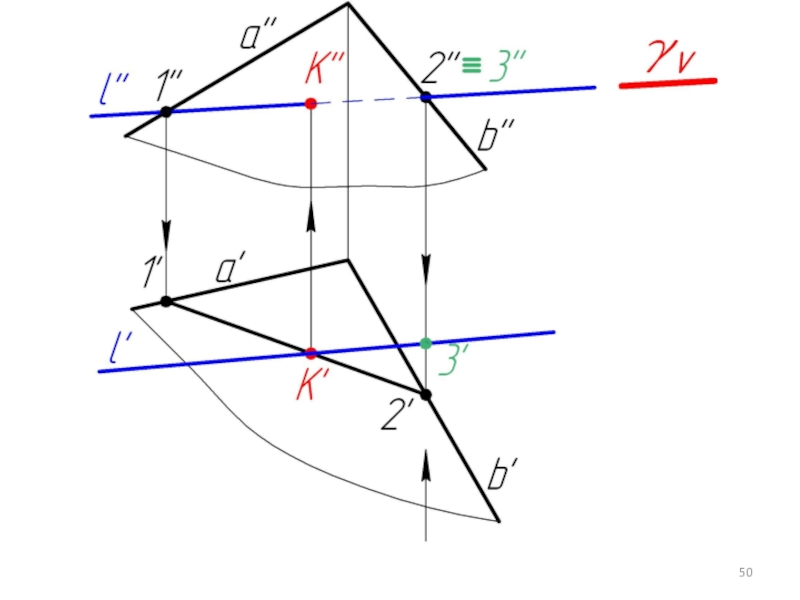
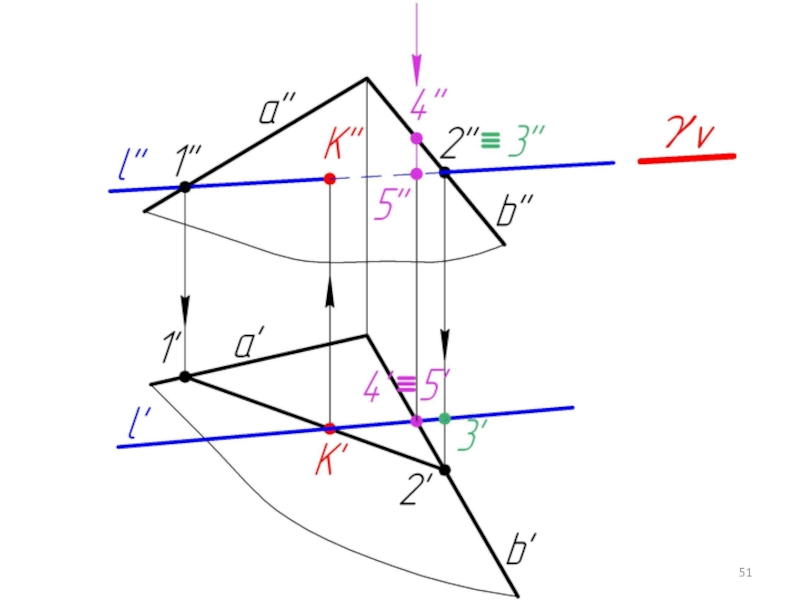
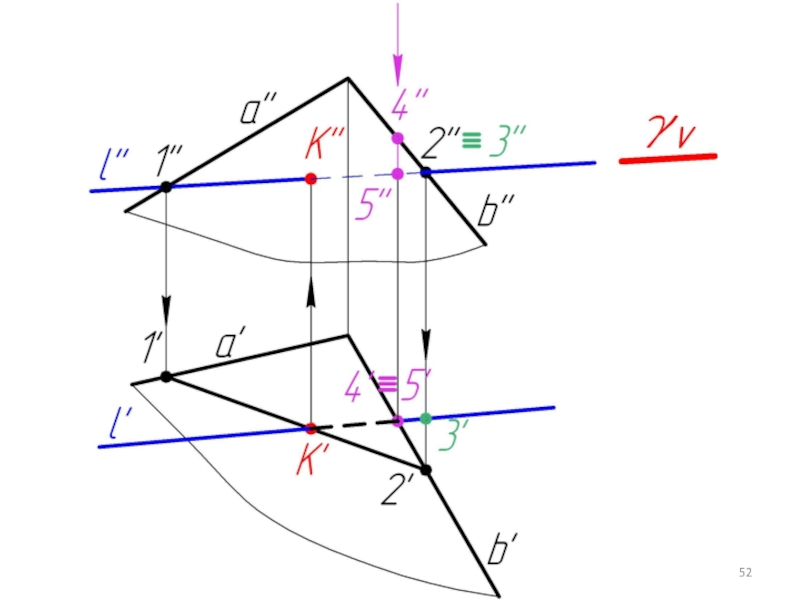
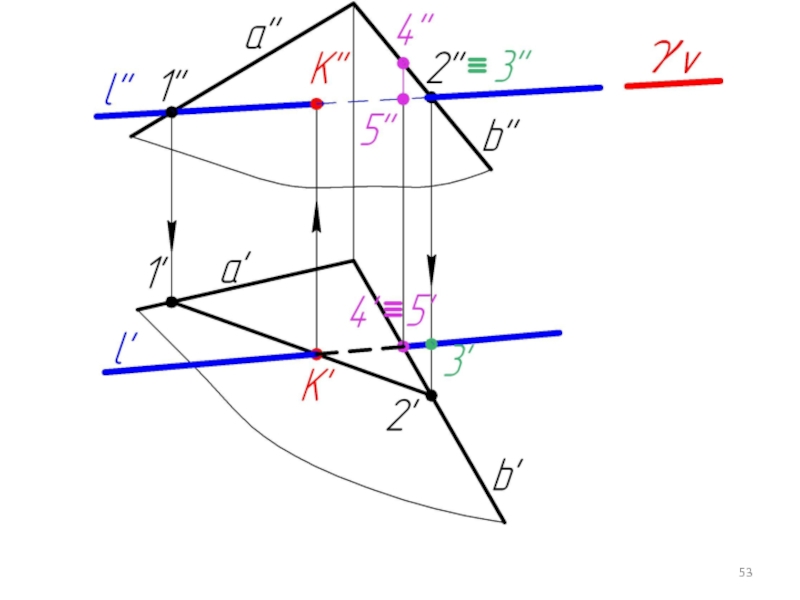
Слайд 445.5. Пересечение прямой с плоскостью в общем случае. Определение видимости.
Дано:
α,
l
Найти:
К = α ∩ l
Алгоритм решения:
l ⊂ γ
γ ∩ α = 1-2
1-2 ∩ l = K
Определяем видимость l
Найти:
К = α ∩ l
Алгоритм решения:
l ⊂ γ
γ ∩ α = 1-2
1-2 ∩ l = K
Определяем видимость l
Слайд 54
D(130, 65, 30)
E (90, 5, 70)
F (35,55, 5)
Домашнее задание
А(115, 20, 10)
В (75, 75, 70)
С (20,10, 25)
