- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное положение прямых и плоскостей презентация
Содержание
- 1. Взаимное положение прямых и плоскостей
- 2. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая
- 3. ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Две плоскости
- 4. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ТЕОРЕМА. Если прямая
- 5. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ ТЕОРЕМА. Если плоскости
- 6. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Рис. 4.7 β (а
- 7. ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ Пример: Построить проекции плоскости,
- 8. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ Пересечение плоскостей, одна из
- 9. Пересечение плоскостей, одна из которых проецирующая Рис.
- 10. Пересечение двух плоскостей общего положения Алгоритм решения:
- 11. Рис. 4.11 Пересечение двух плоскостей общего положения
- 12. Пересечение двух плоскостей общего положения Рис. 4.12
- 13. ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ 1. Пересечение прямой
- 14. 2. Пересечение проецирующей прямой с плоскостью общего
- 15. Пересечение прямой общего положения с плоскостью общего
- 16. Задача. Построить проекции точки пересечения прямой
Слайд 2ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ТЕОРЕМА. Если прямая параллельна плоскости, то проекции данной
a ║ α < = > a' ║ lα ' ᴧ a'' ║ lα ''
a ║ α (h, f) , l α < = > a' ║ l ' ᴧ a'' ║ l ''
h'
A'
1'
f '
2'
l'
a'
l"
a"
A"
1"
2"
f "
h"
x
Построить проекции прямой a,
проходящей через точку A и
параллельную плоскости α
Горячкина А.Ю.
Слайд 3ПАРАЛЛЕЛЬНОСТЬ ДВУХ ПЛОСКОСТЕЙ
ТЕОРЕМА. Две плоскости параллельны, если проекции двух пересекающихся
СЛЕДСТВИЕ. Если две плоскости параллельны, то их одноименные следы параллельны
Рис. 4.2
α (a ∩ b) ║ β (c ∩ d) < = > a' ║ c' , b' ║ d' ᴧ a''║ c'' , b'' ║ d''
α ║ β < = > h0α ║ h0β ᴧ f0α ║ f0β
Рис. 4.1
Горячкина А.Ю.
Слайд 4ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ТЕОРЕМА. Если прямая перпендикулярна плоскости, то горизонтальная проекция
прямой
n ┴ α(h, f) < = > n' ┴ h' ᴧ n'' ┴ f ''
В общем случае отношение перпендикулярности в пространстве не сохраняет признаков перпендикулярности на чертеже.
Пример: Построить проекции прямой, перпендикулярной к заданной плоскости
и проходящей через точку A.
Рис. 4.5
Рис. 4.3
Рис. 4.4
Горячкина А.Ю.
Слайд 5ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
ТЕОРЕМА. Если плоскости взаимно перпендикулярны, то одна из
Пример: Построить проекции плоскости, перпендикулярной к заданной плоскости и проходящей через точку A и прямую a.
Рис. 4.7
Рис. 4.6
Горячкина А.Ю.
Слайд 6ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
Рис. 4.7
β (а , n) ┴ α (c ,
A'
n'
a'
f '
h'
d'
c'
1'
3'
K'
2'
x
1"
a"
h"
2"
n"
K"
f "
A"
3"
c"
d"
Горячкина А.Ю.
Слайд 7ПЕРПЕНДИКУЛЯРНОСТЬ ДВУХ ПЛОСКОСТЕЙ
Пример: Построить проекции плоскости, перпендикулярной к заданной плоскости и
β (а , n) ┴ α (h0α , f0α ) < = > n' ┴ h0α , n'' ┴ f0α
Горячкина А.Ю.
Слайд 8ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Пересечение плоскостей, одна из которых проецирующая
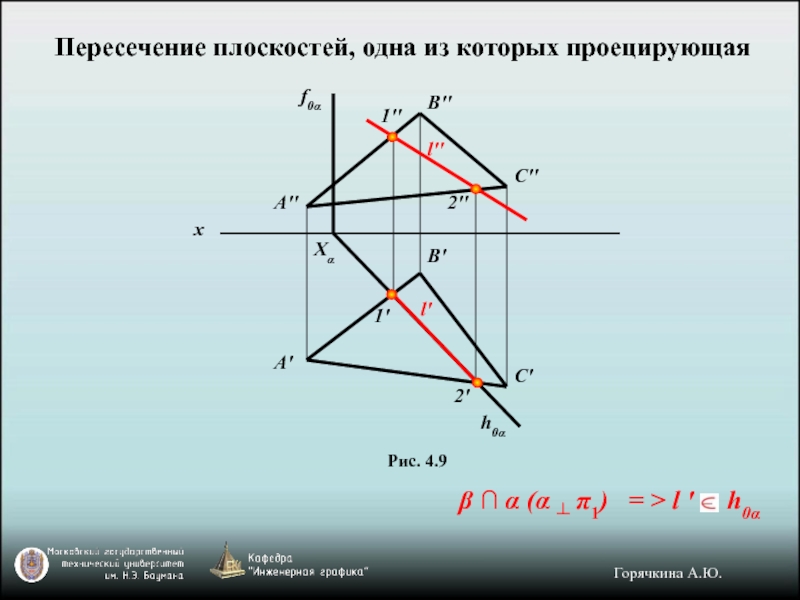
Примечание. Одна из проекций
Вторая проекция находится по принадлежности искомой линии другой, непроецирующей плоскости.
Рис. 4.9
Рис. 4.8
Горячкина А.Ю.
Слайд 9Пересечение плоскостей, одна из которых проецирующая
Рис. 4.9
β ∩ α (α ┴
A"
B"
2"
C"
1"
l"
A'
C'
B'
1'
2'
l'
Xα
h0α
f0α
x
Горячкина А.Ю.
Слайд 10Пересечение двух плоскостей общего положения
Алгоритм решения:
Ввести плоскость-посредник γ1 (γ1 ┴ π)
Построить
γ1 ∩ α = n1
γ1 ∩ β = m1
Найти точку K1 пересечения построенных линий
m1 ∩ n1 = K1
Ввести вторую плоскость-посредник γ2 (γ2 ┴ π) и повторить построения (п.п. 2, 3) для нахождения точки K2
γ2 ∩ α = n2
γ2 ∩ β = m2
m2 ∩ n2 = K2
5. Провести искомую прямую K1 K2 через две найденные точки
Пример: Построить линии пересечения заданных плоскостей
α ∩ β = K1K2
Рис. 4.11
Горячкина А.Ю.
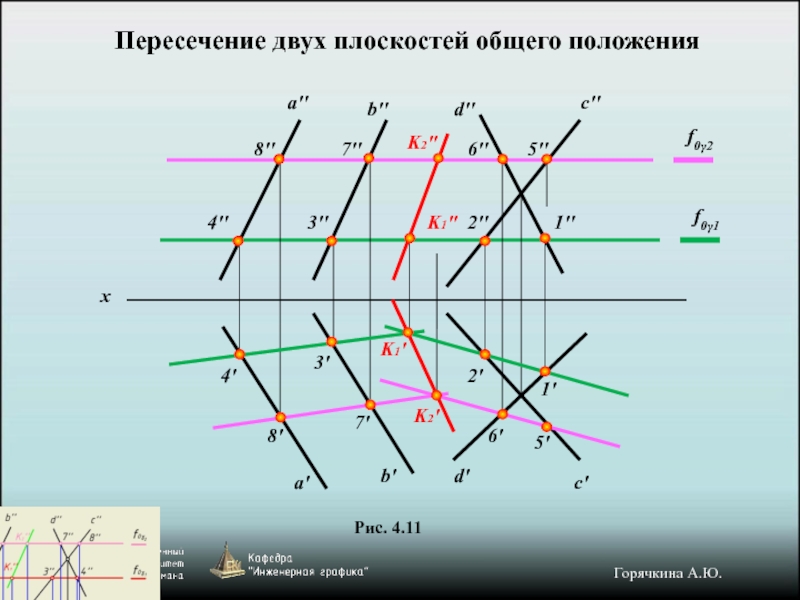
Слайд 11Рис. 4.11
Пересечение двух плоскостей общего положения
f0γ1
f0γ2
a"
1"
c"
2"
3"
4"
d"
b"
5"
6"
7"
8"
K2"
K1"
a'
d'
x
c'
b'
1'
2'
3'
K1'
4'
6'
5'
7'
8'
K2'
Горячкина А.Ю.
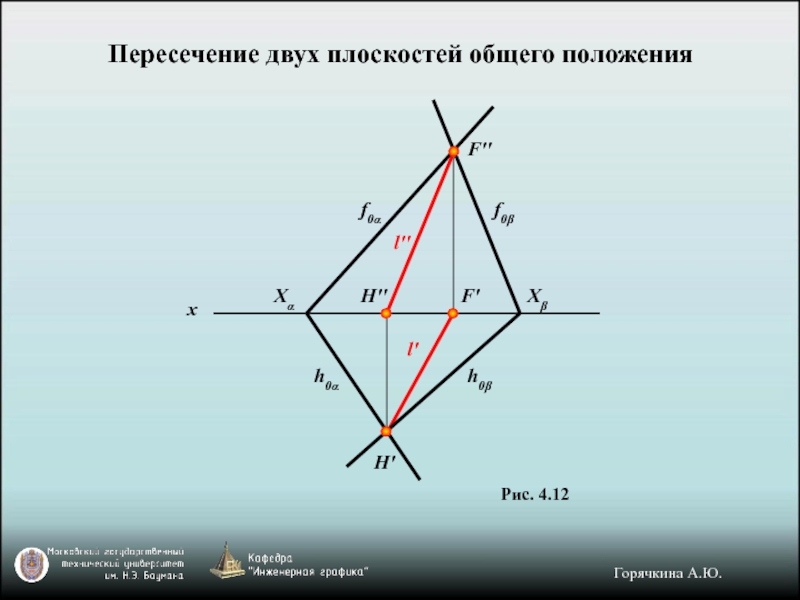
Слайд 12Пересечение двух плоскостей общего положения
Рис. 4.12
F"
Xβ
Xα
f0α
f0β
h0α
h0β
H"
l"
F'
H'
l'
x
Горячкина А.Ю.
Слайд 13ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
1. Пересечение прямой общего положения с проецирующей плоскостью
Одна
Рис. 4.13
Рис. 4.14
α ∩ а = K , α ┴ π1 = > K ' h0α
f0α
h0α
Xα
a'
K'
K"
a"
x
Горячкина А.Ю.
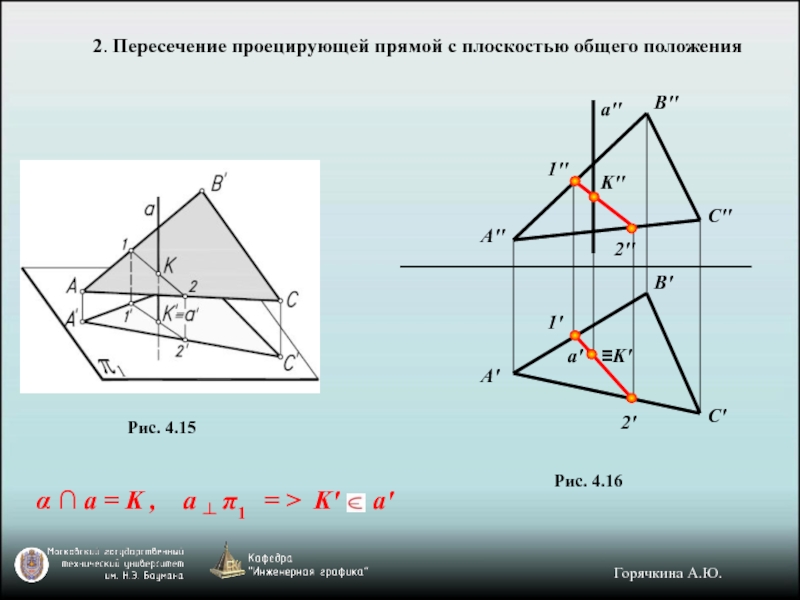
Слайд 142. Пересечение проецирующей прямой с плоскостью общего положения
Рис. 4.15
α ∩ а
Рис. 4.16
A"
C"
B"
a"
1"
2"
K"
B'
C'
A'
2'
1'
a'
≡K'
Горячкина А.Ю.
Слайд 15Пересечение прямой общего положения с плоскостью общего положения
Алгоритм
определения точки пересечения
Заключить прямую a в проецирующую плоскость-посредник β
а β, β ┴ π1
2. Определить линию l пересечения заданной плоскости α и вспомогательной плоскости β
a ∩ β = l
Найти точку K пересечения заданной прямой a и построенной линии l пересечения плоскостей
a ∩ l = K
Рис. 4.17
Горячкина А.Ю.
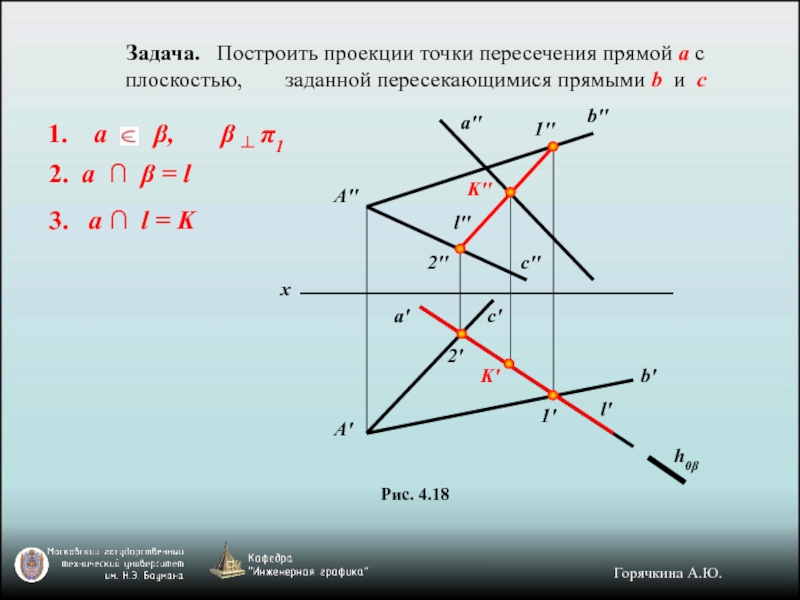
Слайд 16Задача. Построить проекции точки пересечения прямой а с плоскостью, заданной
Рис. 4.18
1. а β, β ┴ π1
2. a ∩ β = l
3. a ∩ l = K
A"
b"
c"
a"
2"
1"
K"
A'
b'
1'
x
K'
c'
2'
a'
h0β
l'
l"
Горячкина А.Ю.