- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение графика квадратичной функции. (8 класс) презентация
Содержание
- 1. Построение графика квадратичной функции. (8 класс)
- 2. Определение квадратичной функции Функцию вида y =
- 3. Алгоритм построения параболы 1. Найти координаты
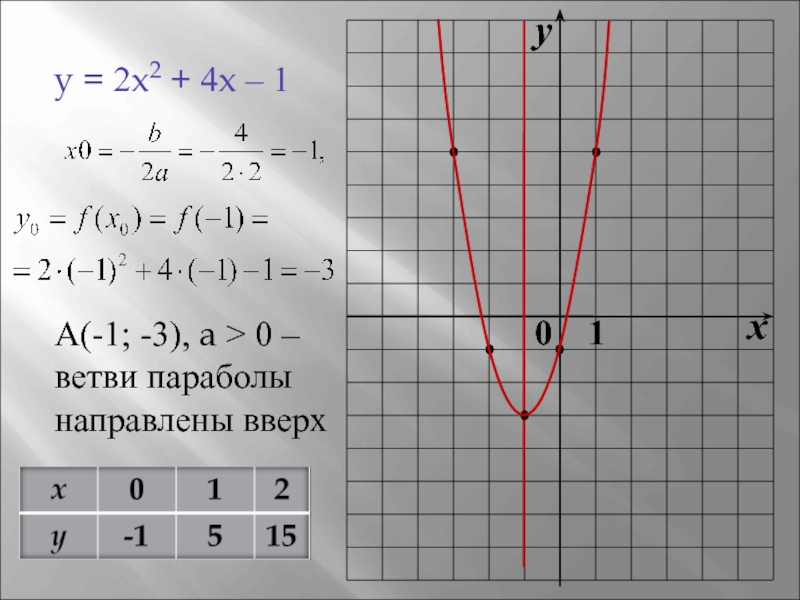
- 4. y = 2x2 + 4x – 1
- 5. Ответьте на вопросы Куда направлены ветви параболы?
- 6. Постройте график функции y =
- 7. x y Определить координаты вершины параболы. Уравнение
Слайд 2Определение квадратичной функции
Функцию вида y = ax2 + bx + c,
где a, b, c - произвольные числа, причём a ≠ 0, называют квадратичной функцией («a» называют старшим коэффициентом).
Примеры:
y = 3x2 + 5x + 6,
y = 5x2 – 7x,
y = 1/2x2 + 1.
Примеры:
y = 3x2 + 5x + 6,
y = 5x2 – 7x,
y = 1/2x2 + 1.
Слайд 3Алгоритм построения параболы
1. Найти координаты вершины параболы А(х0, у0) по
формулам
построить эту точку в координатной плоскости, провести ось симметрии параболы.
2. С правой и с левой стороны от оси симметрии взять 2-3 значения аргумента (х1, х2, х3), вычислить значения функции f(х1), f(х2), f(х3). Отметить точки в координатной плоскости.
3. Построить параболу.
построить эту точку в координатной плоскости, провести ось симметрии параболы.
2. С правой и с левой стороны от оси симметрии взять 2-3 значения аргумента (х1, х2, х3), вычислить значения функции f(х1), f(х2), f(х3). Отметить точки в координатной плоскости.
3. Построить параболу.
Слайд 5Ответьте на вопросы
Куда направлены ветви параболы?
Найдите координаты вершины параболы.
Запишите уравнение прямой,
которая является осью симметрии параболы.
y = -x2 + 2x + 1
y = -3x2 – 6x + 1
y = 3x2 – 12x
y = -2x2 + 8x – 5
y = x2 + 4x + 5
(1; 2), x = 1
(-1; 4), x = -1
(2; -12), x = 2
(2; 3), x = 2
(-2; 1), x = -2
Слайд 6
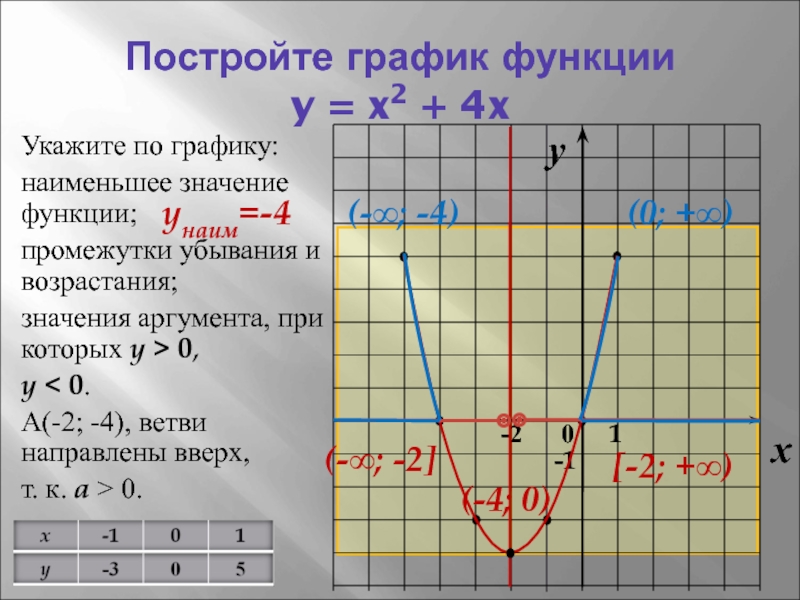
Постройте график функции
y = x2 + 4x
Укажите по графику:
наименьшее значение
функции;
промежутки убывания и возрастания;
значения аргумента, при которых y > 0,
y < 0.
А(-2; -4), ветви направлены вверх,
т. к. a > 0.
промежутки убывания и возрастания;
значения аргумента, при которых y > 0,
y < 0.
А(-2; -4), ветви направлены вверх,
т. к. a > 0.
yнаим=-4
(-∞; -2]
[-2; +∞)
(-∞; -4)
(0; +∞)
(-4; 0)
Слайд 7x
y
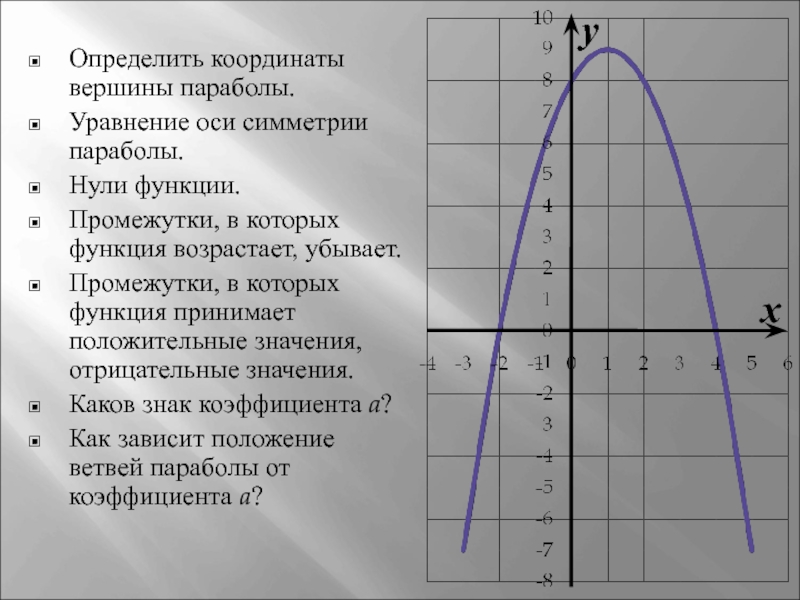
Определить координаты вершины параболы.
Уравнение оси симметрии параболы.
Нули функции.
Промежутки, в которых функция
возрастает, убывает.
Промежутки, в которых функция принимает положительные значения, отрицательные значения.
Каков знак коэффициента a?
Как зависит положение ветвей параболы от коэффициента a?
Промежутки, в которых функция принимает положительные значения, отрицательные значения.
Каков знак коэффициента a?
Как зависит положение ветвей параболы от коэффициента a?