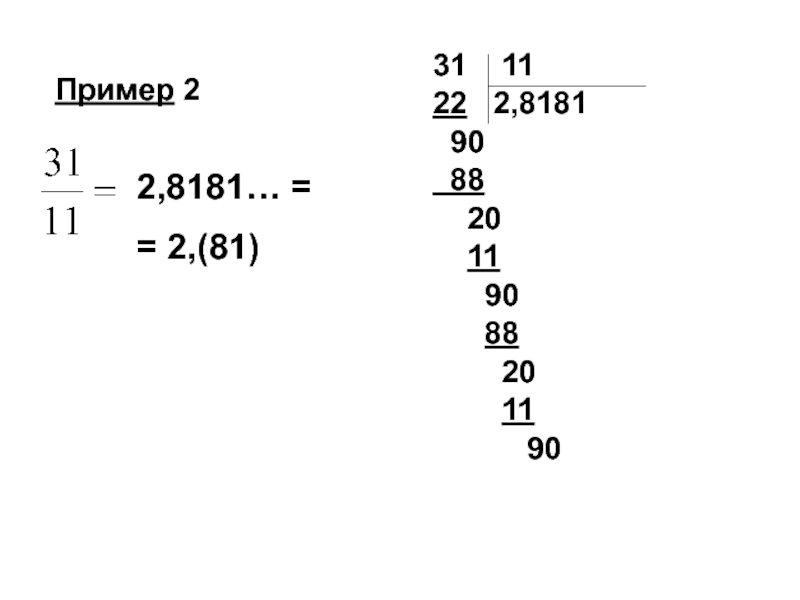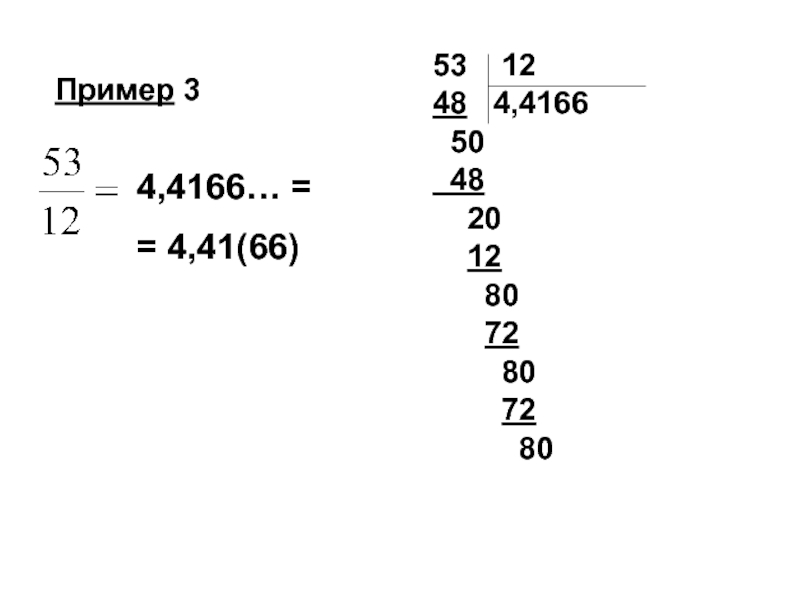- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расширение множества натуральных чмсел презентация
Содержание
- 1. Расширение множества натуральных чмсел
- 2. Задача расширения понятия числа Положительные рациональные числа Действительные числа
- 3. Задача расширения понятия числа Большинство применений математики
- 5. 4 куска ткани
- 6. Для решения первой задачи достаточно множества целых
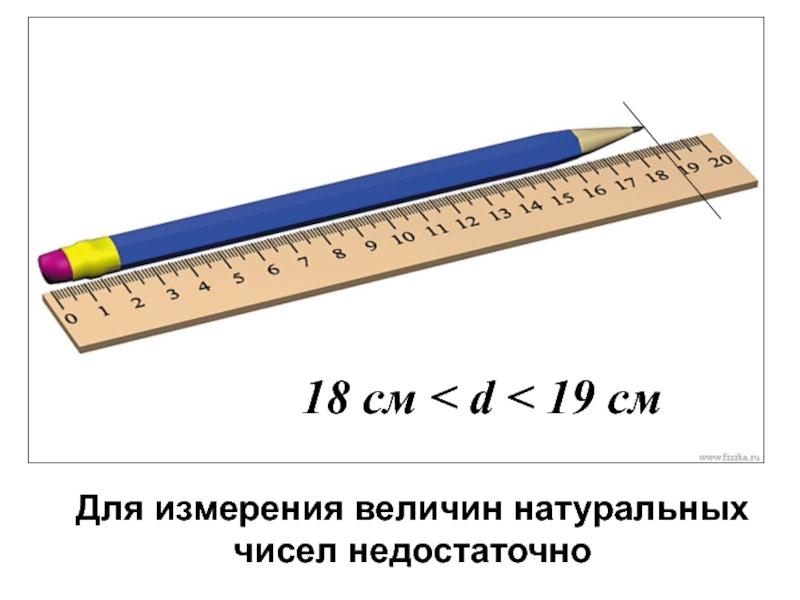
- 7. 18 см < d < 19 см Для измерения величин натуральных чисел недостаточно
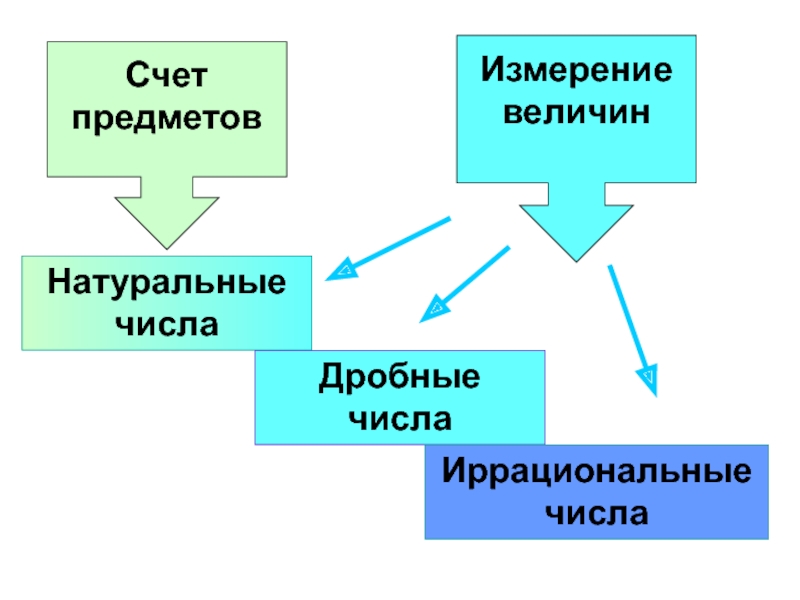
- 8. Натуральные числа Дробные числа Иррациональные числа
- 9. Q Взаимосвязи между числовыми множествами R Z
- 10. Q+ Расширение множества натуральных чисел R+ R
- 11. ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ ЧИСЛА Понятие дроби
- 12. Понятие дроби Дан отрезок а, выберем единичный
- 14. Длина отрезка а при единице длины е
- 15. 3. Единичный отрезок е и любая его
- 16. Рассмотрим отрезок а, выберем единичный отрезок е
- 18. Дроби, выражающие длину одного и того же
- 20. Основное свойство дроби На этом свойстве
- 21. Сокращение дроби – это замена данной дроби
- 22. Пример 1: несократимая дробь, т. к.
- 23. Приведение дробей к общему знаменателю – это
- 24. 15 = 3 · 5, 35 =
- 25. Дробь называется правильной, если её числитель меньше
- 27. Понятие положительного рационального числа
- 28. - Обыкновенная дробь, числитель, знаменатель - Правильная
- 29. Одному и тому же отрезку можно поставить
- 30. Положительным рациональным числом называется класс равных дробей,
- 36. Арифметические действия над положительными рациональными числами
- 37. Сложение Рассмотрим отрезки а, b и
- 38. Если же числа а и b
- 39. Чтобы сложить дроби, нужно привести их к
- 40. В общем виде правило сложения можно
- 41. Теорема (о существовании и единственности суммы) Сумма
- 42. Отношение «больше» Пусть а, b ∈ Q+.
- 43. Практические приемы установления отношения «больше»
- 44. Теорема. (∀ а, b ∈ Q+) а
- 45. Отношение «больше» обладает свойствами: 1) антисимметричности:
- 46. 2) Ассоциативный закон сложения (∀
- 47. 5) (∀ а, b ∈ Q+)
- 52. Разностью положительных рациональных чисел а и b
- 53. Теорема (о существовании и единственности разности) Разность
- 55. Правила вычитания 1) правило вычитания числа из
- 56. 2) правило вычитания суммы из числа а
- 57. Умножение
- 58. Примеры: 1)
- 59. Теорема (о существовании и единственности произведения) Произведение
- 60. 2) Ассоциативный закон умножения (∀
- 61. 5) Сократимость умножения (∀ а, b, с
- 62. Деление Частным положительных рациональных чисел а
- 63. Теорема (о существовании и единственности частного) Частное
- 64. 2) правило деления числа на произведение а
- 65. 5) а : 1 = а, а
- 66. Термин «рациональное число» произошел от латинского слова
- 67. СВОЙСТВА МНОЖЕСТВА ПОЛОЖИТЕЛЬНЫХ РАЦИОНАЛЬНЫХ ЧИСЕЛ 1. N ⊂ Q+
- 68. 2. Множество Q+ не ограничено снизу, т.е.
- 69. 5. Множество Q+ плотно, т.е. между любыми
- 70. Основные задачи на дроби 1.Нахождение дроби от числа
- 71. 2.Нахождение числа по данному значению дроби
- 72. 3.Нахождение отношения двух чисел В классе 25
- 73. Проценты Чтобы проценты выразить дробью, нужно число
- 74. Основные задачи на проценты В классе 25
- 75. 10 учеников класса ходили в кино, что
- 76. 3.Нахождение процентного отношения двух чисел В классе
- 77. Множество положительных рациональных чисел как расширение множества
- 78. 3. Выполнимость в Q+ операции, не всегда
- 79. Упражнение Решить уравнение, используя зависимость между компонентами и результатами действий:
- 80. Десятичные дроби
- 81. Примеры:
- 82. Утверждение: Если к десятичной дроби А,an-1 ...
- 83. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ Сложение и вычитание
- 84. Умножение Примеры: 1) 5,426·102 = 542,6 2) 5,42·103 = 5420
- 85. 24,48 : 1,2 = 244,8 : 12
- 86. ПЕРЕВОД ОБЫКНОВЕННЫХ ДРОБЕЙ В ДЕСЯТИЧНЫЕ И ДЕСЯТИЧНЫХ – В ОБЫКНОВЕННЫЕ
- 87. ? Чтобы перевести обыкновенную дробь в десятичную, нужно разделить числитель на знаменатель
- 89. Примеры: 1) 0,04375
- 90. - дробь нельзя превратить в конечную
- 91. Упражнения
- 94. БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ПЕРИОДИЧЕСКИЕ ДРОБИ 1,42857141… = = 1,(42857141) Пример 1
- 95. 2,8181… = = 2,(81) Пример 2
- 96. 4,4166… = = 4,41(66) Пример 3
- 97. Пример 4 0,25 = 0,250000…. = 0,25(0)
- 98. Если период следует сразу после запятой, то
- 99. Чисто периодическая бесконечная десятичная дробь, меньше
- 100. Смешанная периодическая дробь, меньше единицы, равна такой
- 102. Спасибо за внимание!
Слайд 3Задача расширения понятия числа
Большинство применений математики сводится к двум основным задачам:
-
- измерение величин.
Слайд 6Для решения первой задачи достаточно множества целых неотрицательных чисел:
N0 = {0,
Слайд 11ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ ЧИСЛА
Понятие дроби
Понятие положительного рационального числа
Арифметические действия
Свойства множества положительных рациональных чисел
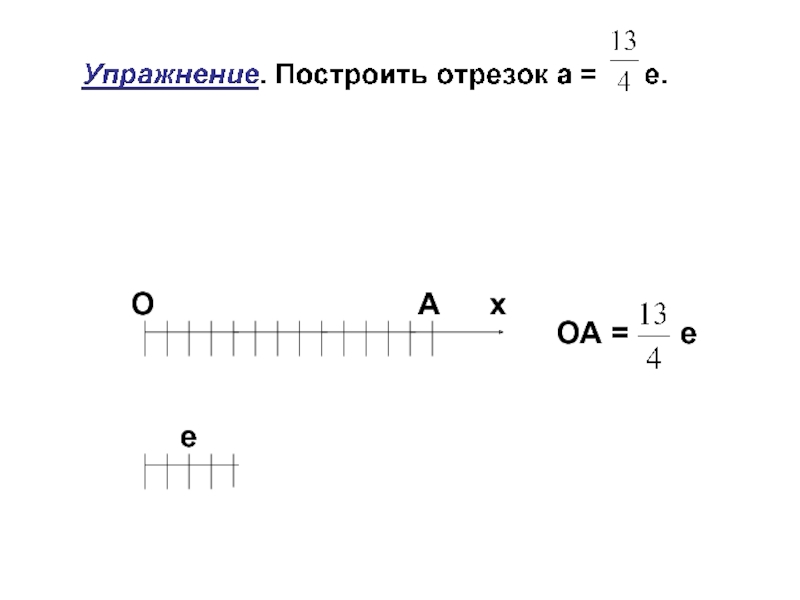
Слайд 12Понятие дроби
Дан отрезок а, выберем единичный отрезок е.
При измерении длины отрезка
1. Единичный отрезок е укладывается в отрезке а целое число раз (n раз):
mе(а) = n или а = nе
Длина отрезка а при единице длины е выражается натуральным числом n
Отрезки а и е в этом случае называются соизмеримыми
Слайд 14Длина отрезка а при единице длины е выражается обыкновенной дробью
Отрезки а
Знаменатель определяет, какую часть единицы измерения следует рассмотреть, числитель – указывает, сколько таких частей нужно взять
Слайд 153. Единичный отрезок е и любая его часть не укладываются в
В этом случае отрезок а не соизмерим ни с каким единичным отрезком.
Длина такого отрезка выражается иррациональным числом.
Слайд 18Дроби, выражающие длину одного и того же отрезка при единице длины
Слайд 20Основное свойство дроби
На этом свойстве основано сокращение дробей и приведение
Слайд 21Сокращение дроби – это замена данной дроби другой, равной данной, но
Чтобы сократить дробь, надо ее числитель и знаменатель разделить на одно и то же число отличное от 0
Дробь является сократимой, если ее числитель и знаменатель имеют общий делитель больше единицы. Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой
Слайд 22
Пример 1:
несократимая дробь, т. к.
D (5; 17) = 1, т.е. 5
D (48; 80) = 16,
Слайд 23Приведение дробей к общему знаменателю – это замена данных дробей равными
Слайд 25Дробь называется правильной, если её числитель меньше знаменателя, и неправильной, если
правильные
неправильные
Слайд 28- Обыкновенная дробь, числитель, знаменатель
- Правильная дробь
- Неправильная дробь
- Сократимая дробь
-
m < n
m ≥ n
D(m; n) ≠ 1
D(m; n) = 1
Слайд 29Одному и тому же отрезку можно поставить в соответствие бесконечное множество
Слайд 30Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая
Множество всех положительных рациональных чисел принято обозначать символом Q+.
Слайд 38
Если же числа а и b представлены дробями с различными знаменателями,
Слайд 39Чтобы сложить дроби, нужно привести их к общему знаменателю, затем сложить
Пример:
Слайд 41Теорема (о существовании и единственности суммы)
Сумма любых двух положительных рациональных чисел
Слайд 42Отношение «больше»
Пусть а, b ∈ Q+.
Определение. Число а больше числа b,
а > b ⇔ (∃ с ∈ Q+) а = b + с
Отношение «меньше» определяется аналогично
Слайд 45Отношение «больше» обладает свойствами:
1) антисимметричности:
2) транзитивности:
(∀ а, b, с ∈
Отношение «больше» является отношением порядка на множестве Q+
Слайд 462) Ассоциативный закон сложения
(∀ а, b, с ∈ Q+)
3) Сократимость сложения
(∀ а, b, с ∈ Q+) а + с = b + с ⇒ а = b
4) Монотонность сложения
(∀ а, b, с ∈ Q+) а > b ⇒ а + с > b + с
Свойства сложения
1) Коммутативный закон сложения
(∀ а, b ∈ Q+) а + b = b + а
Слайд 52Разностью положительных рациональных чисел а и b называется такое положительное рациональное
а – b = с ⇔ а = b + с
Вычитание
Операцию, в результате которой находят разность положительных рациональных чисел а и b, называют вычитанием. Вычитание положительных рациональных чисел - операция, обратная сложению
Слайд 53Теорема (о существовании и единственности разности)
Разность а – b положительных рациональных
Слайд 55Правила вычитания
1) правило вычитания числа из суммы
а > с ⇒
или
b > с ⇒ (а + b) – с = а + (b – с)
Слайд 562) правило вычитания суммы из числа
а – (b + с) =
3) правило вычитания разности из числа
а – (b – с) = (а – b) + с
а – 0 = а, а – а = 0
Слайд 59Теорема (о существовании и единственности произведения)
Произведение любых двух положительных рациональных чисел
Слайд 602) Ассоциативный закон умножения
(∀ а, b, с ∈ Q+)
3) дистрибутивный закон умножения относительно сложения
(∀ а, b, с ∈ Q+) а · (b + с) = а · b + а · с
(∀ а, b, с ∈ Q+) а · (b - с) = а · b - а · с
4) дистрибутивный закон умножения относительно вычитания
Законы умножения
1) Коммутативный закон умножения
(∀ а, b ∈ Q+) а · b = b · а
Слайд 615) Сократимость умножения
(∀ а, b, с ∈ Q+) а · с
6) Монотонность умножения
(∀ а, b, с ∈ Q+) а > b ⇒ а · с > b · с
7) а · 1 = 1 · а = а, а · 0 = 0 · а = 0
Слайд 62Деление
Частным положительных рациональных чисел а и b называется такое положительное
а : b = с ⇔ а = b · с
Деление положительных рациональных чисел - операция, обратная умножению Операцию, в результате которой находят частное положительных рациональных чисел а и b, называют делением.
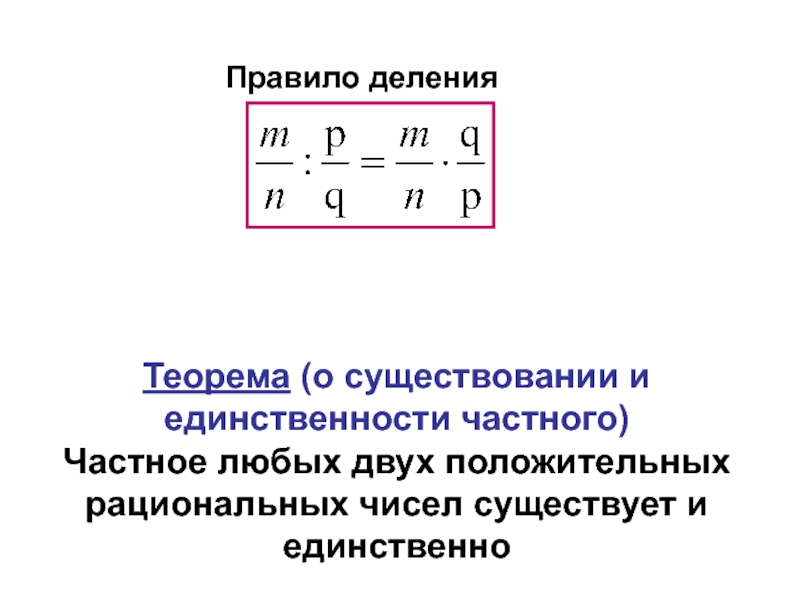
Слайд 63Теорема (о существовании и единственности частного)
Частное любых двух положительных рациональных чисел
Правило деления
Слайд 642) правило деления числа на произведение
а : (b · с) =
3) дистрибутивный закон деления относительно сложения
(а + b) : с = а : с + b : с
4) дистрибутивный закон деления относительно вычитания
(а - b) : с = а : с - b : с
Свойства деления
1) правило деления произведения на число:
(а · b) : с = (а : с) · b или (а · b) : с = а · (b : с)
Слайд 66Термин «рациональное число» произошел от латинского слова r а t i
Слайд 682. Множество Q+ не ограничено снизу, т.е. в нем нет наименьшего
3. Множество Q+ не ограничено сверху, т.е. в нем нет наибольшего числа
Множество Q+ упорядочивает заданное на нем отношение «больше» (или «меньше»), которое является отношением порядка, так как оно антисимметрично и транзитивно.
4. Множество Q+ упорядочено
Слайд 695. Множество Q+ плотно, т.е. между любыми двумя различными числами а
6. Множество Q+ замкнуто относительно четырех арифметических операций
т.е. сумма, разность, произведение, частное (кроме частного при делении на 0, которое не имеет смысла) любых двух положительных рациональных чисел является положительным рациональным числом.
Слайд 723.Нахождение отношения двух чисел
В классе 25 учеников.
Слайд 73Проценты
Чтобы проценты выразить дробью, нужно число процентов разделить на 100 и
Чтобы число выразить в процентах, нужно число умножить на 100 и приписать знак %.
Слайд 74Основные задачи на проценты
В классе 25 учеников.
25 · 40 % = 25 · 0,4 = 10 (уч.)
1.Нахождение процентов от числа
Слайд 7510 учеников класса ходили в кино, что составляет 40 % всех
2.Нахождение числа по данному значению процентов
10 : 40% = 10 : 0,4= 100 : 4 = 25 (уч.)
Слайд 763.Нахождение процентного отношения двух чисел
В классе 25 учеников.
Слайд 77Множество положительных рациональных чисел
как расширение множества натуральных чисел
Условия расширения:
1. N ⊂
2. Согласованность операций,
т.е. результаты арифметических действий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но выполненных по правилам, сформулированным для положительных рациональных чисел.
Слайд 783. Выполнимость в Q+ операции, не всегда осуществимой в N
Деление,
Слайд 79Упражнение
Решить уравнение, используя зависимость между компонентами и результатами действий:
Слайд 82Утверждение: Если к десятичной дроби А,an-1 ... a0 приписать справа любое
А,an-1 ... a0 = А,an-1 ... a000…0
Слайд 8524,48 : 1,2 = 244,8 : 12 = 20,4
Примеры: 1)
24
4
2
0,
8
4
48
0
Деление
2) 542,6 : 102 = 5,426
3) 5,4 : 103 = 0,0054
Слайд 97Пример 4
0,25 = 0,250000…. = 0,25(0)
Дробь называется периодической, если начиная с
Каждое положительное рациональное число можно представить в виде бесконечной десятичной периодической дроби.
Слайд 98Если период следует сразу после запятой, то такую дробь называют чисто
Если перед периодом стоят один или несколько знаков, то дробь - смешанная периодическая
Слайд 99
Чисто периодическая бесконечная десятичная дробь, меньше единицы, равна такой обыкновенной дроби,
Преобразование бесконечной периодической дроби в обыкновенную
Пример: 5,33… = 5,(3) =
Слайд 100Смешанная периодическая дробь, меньше единицы, равна такой обыкновенной дроби, числитель которой
К периодическим десятичным дробям можно отнести все конечные десятичные дроби, как дроби, имеющие в периоде число 0.