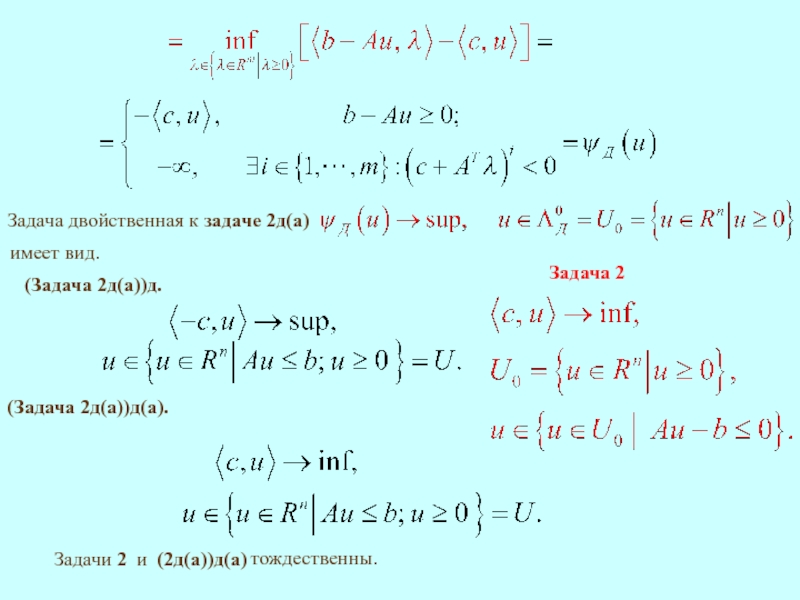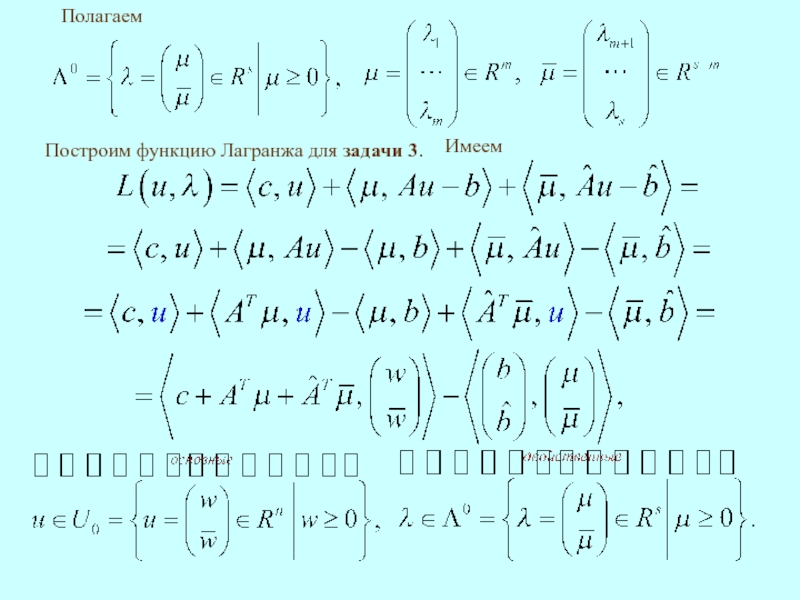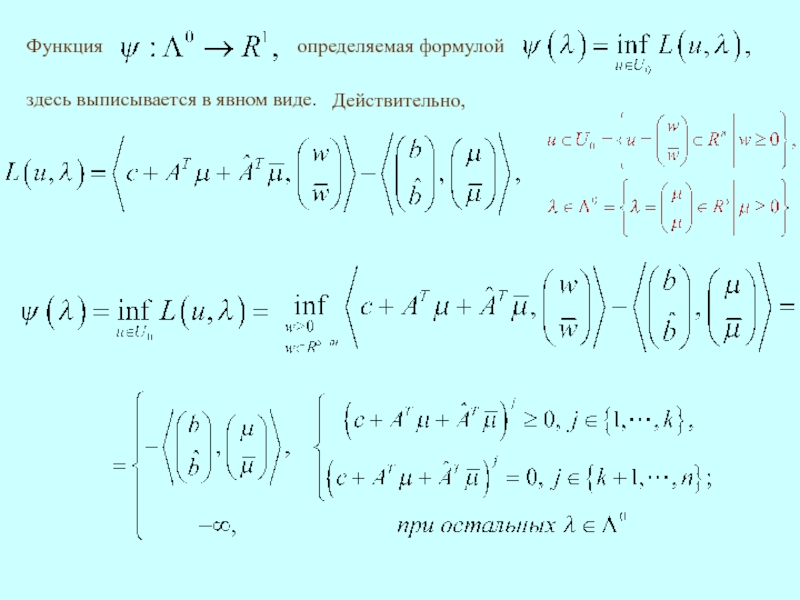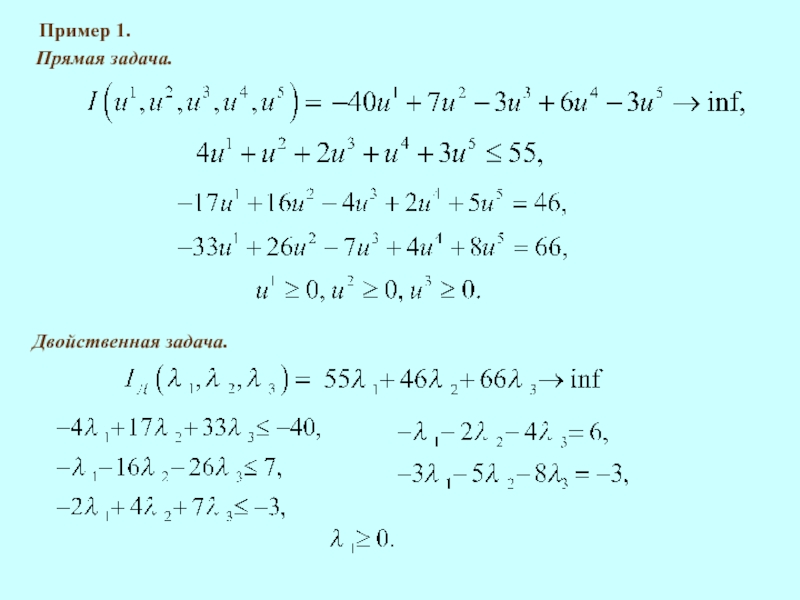- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Теория двойственности в линейном программировании. Лекция 28 презентация
Содержание
Слайд 2
11. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ
ПРОГРАММИРОВАНИИ
11.1. Двойственная задача к канонической
программирования.
11.2. Двойственная задача к стандартной задаче линейного
программирования.
11.3. Двойственная задача к общей задаче линейного
программирования.
11.4. Правило построения двойственной задачи.
Слайд 3
11.1. Двойственная задача к канонической задаче линейного программирования.
Рассмотрим каноническую задачу
Задача 1.
Здесь
Построим функцию Лагранжа для задачи 1.
Имеем
определяемая формулой
здесь выписывается в явном виде.
Действительно,
Слайд 4
Задача 1д(а).
формулируется так.
Данная задача эквивалентна следующей.
Задача 1д.
Эквивалентность задачи
Слайд 5
Задача 1д(а). является задачей линейного программирования
Здесь
Покажем, что задача двойственная
будет эквивалентна задаче 1.
Тогда
Слайд 7
11.2. Двойственная задача к стандартной задаче линейного программирования.
Рассмотрим стандартную задачу
Задача 2.
Здесь
Построим функцию Лагранжа для задачи 2.
Имеем
здесь выписывается в явном виде.
определяемая формулой
Действительно,
Слайд 8
следует искать среди тех векторов
Двойственная задача
формулируется так.
Данная задача
Задача 2д.
Задача 2д(а).
Слайд 11
11.3. Двойственная задача к общей задаче линейного программирования.
Рассмотрим общую задачу
Здесь
Задача 3.
Слайд 15
Данная задача эквивалентна следующей.
Задача 3д(а).
Эквивалентность задачи 3д и задача 3д(а)
По аналогии с предыдущими пунктами доказывается,
Слайд 18
В двойственной задаче 3д(а)
Матрица ограничений в двойственной задаче
Вектором правых частей ограничений
Ограничения двойственной задачи,
записываются в форме неравенств,
Наконец, переменные двойственной задачи,
объявляются положительными,
а на остальные переменные ограничения не налагаются.