- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклость функции. Точки перегиба презентация
Содержание
- 1. Выпуклость функции. Точки перегиба
- 3. Функция y=f(x) называется выпуклой вверх на
- 5. ТЕОРЕМА 1. Функция выпукла вверх (вниз) на
- 6. ТЕОРЕМА 2. достаточное условие выпуклости
- 7. Точкой перегиба графика непрерывной функции называется точка,
- 8. ТЕОРЕМА 3. необходимое условие перегиба
- 9. ТЕОРЕМА 4. достаточное условие перегиба
- 10. схема исследования функции на выпуклость
- 11. 3 Исследовать знак второй производной слева и
- 12. Пример. Найти интервалы выпуклости и точки перегиба функции
- 13. Решение: 1 Находим вторую производную: 2 Находим
- 14. 3 Исследуем знак второй производной слева
Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых х1, х2 из этого промежутка выполняется неравенство:
Слайд 19.5. ВЫПУКЛОСТЬ ФУНКЦИИ.
ТОЧКИ ПЕРЕГИБА.
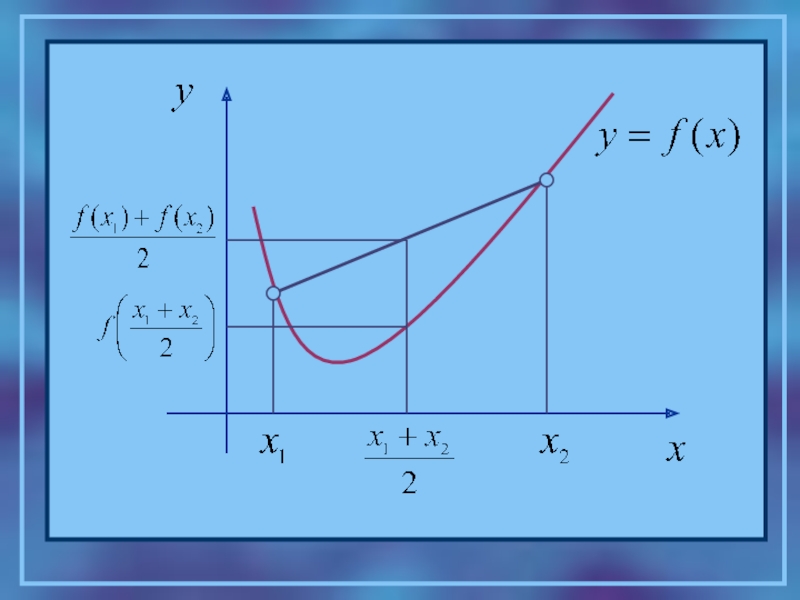
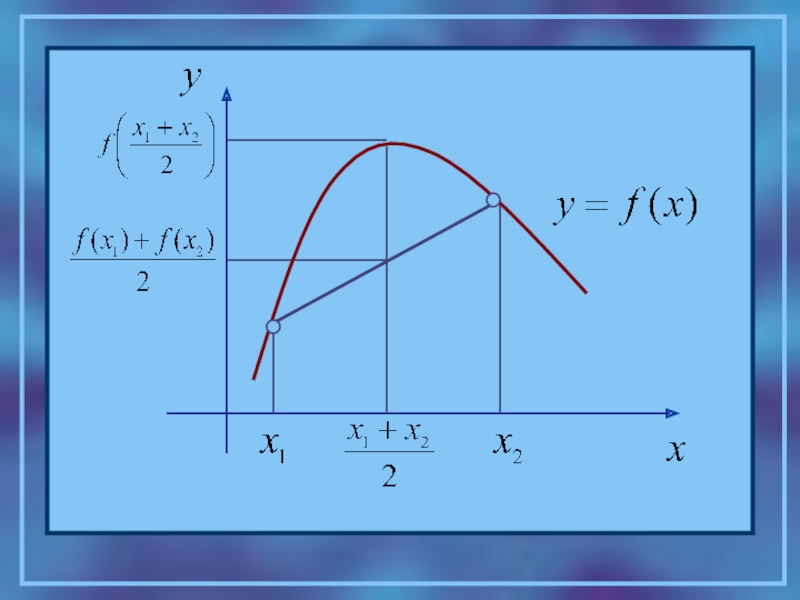
Функция y=f(x) называется выпуклой вниз (вогнутой) на
промежутке Х, если для любых х1, х2 из этого промежутка выполняется неравенство:
Слайд 3
Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых
х1, х2 из этого промежутка выполняется неравенство:
Слайд 5ТЕОРЕМА 1.
Функция выпукла вверх (вниз) на
промежутке Х тогда и только
тогда,
когда ее первая производная на этом
промежутке монотонно возрастает
(убывает).
когда ее первая производная на этом
промежутке монотонно возрастает
(убывает).
Слайд 6ТЕОРЕМА 2.
достаточное условие
выпуклости функции
Если вторая производная дифференцируемой
функции положительна
(отрицательна)
на некотором промежутке Х, то функция
выпукла вниз (вверх) на этом промежутке.
на некотором промежутке Х, то функция
выпукла вниз (вверх) на этом промежутке.
Слайд 7Точкой перегиба графика непрерывной функции
называется точка, разделяющая интервалы,
на которых функция выпукла
вверх и вниз.
Точка перегиба – это точка экстремума первой производной.
Слайд 8ТЕОРЕМА 3.
необходимое условие
перегиба
Вторая производная дифференцируемой функции в точке перегиба
х0 равна нулю:
Слайд 9ТЕОРЕМА 4.
достаточное условие
перегиба
Если вторая производная дифференцируемой функции в точке
х0 меняет свой знак, то х0 - точка перегиба ее графика.
Слайд 10схема исследования функции на
выпуклость и точки перегиба:
1
Найти вторую производную
функции.
2
Найти точки, в которых вторая
производная функции равна нулю или
не существует.
Слайд 113
Исследовать знак второй производной
слева и справа от найденных точек
и сделать вывод
об интервалах
выпуклости и точках перегиба.
выпуклости и точках перегиба.
4
Найти значения функции в точках
перегиба.
Слайд 13Решение:
1
Находим вторую производную:
2
Находим точки, в которых вторая производная обращается в нуль:
Слайд 14
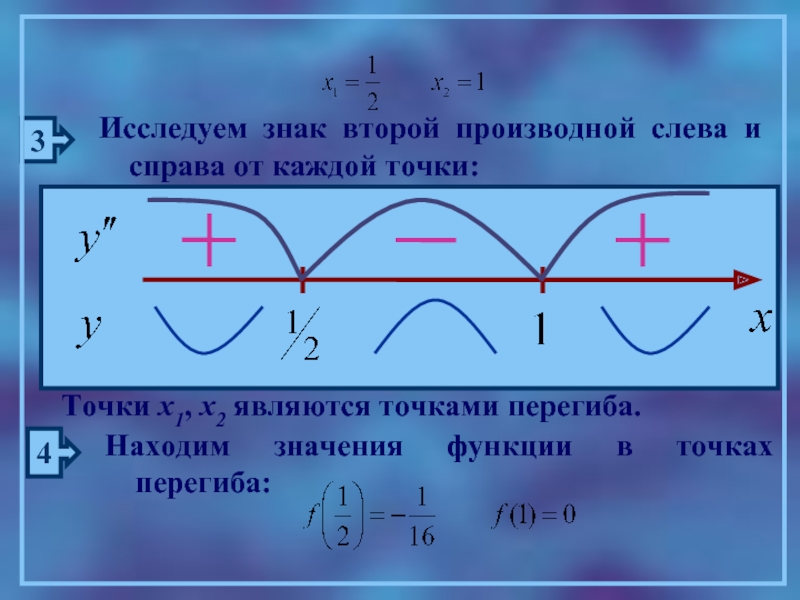
3
Исследуем знак второй производной слева и справа от каждой точки:
Точки х1,
х2 являются точками перегиба.
4
Находим значения функции в точках перегиба:
