Осетрова
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление пределов. Раскрытие неопределенностей презентация
Содержание
- 1. Вычисление пределов. Раскрытие неопределенностей
- 2. Было домашнее задание на сегодня: + знать
- 3. Предел функции Предел – одно из основных
- 4. Было домашнее задание на сегодня: + знать
- 5. ТЕОРЕМА 1. Предел СУММЫ
- 6. ТЕОРЕМА 2. Предел константы равен самой этой константе.
- 7. ТЕОРЕМА 3. Предел ПРОИЗВЕДЕНИЯ
- 8. ТЕОРЕМА 4. Предел ОТНОШЕНИЯ
- 9. ТЕОРЕМА 5. Постоянный множитель можно выносить за знак предела
- 10. ТЕОРЕМА 6. Предел СТЕПЕНИ переменного равен той же степени предела основания:
- 11. Упражнения (13 примеров):
- 12. Упражнения (13 примеров):
- 13. 06.09.2016
- 14. Домашнее задание Дорешать примеры (всего должно быть 13 примеров) Выписать таблицу производных позади тетради 06.09.2016
Слайд 1Вычисление пределов.Раскрытие неопределенностей
СГБОУ ПО «СМК имени Жени Дерюгиной»
Преподаватель математики
С. А.
Слайд 2Было домашнее задание на сегодня:
+ знать ответы на следующие вопросы:
С какими
математиками связано понятие «Предел»?
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
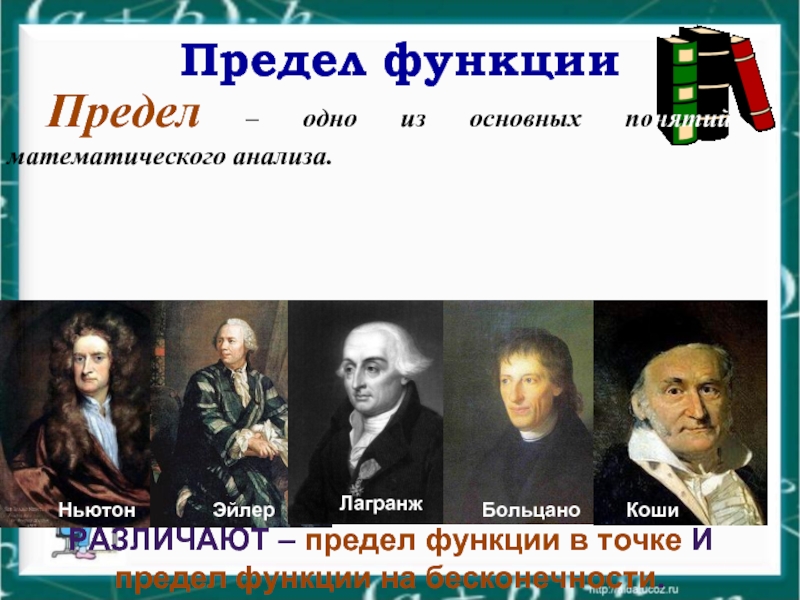
Слайд 3Предел функции
Предел – одно из основных понятий математического анализа.
РАЗЛИЧАЮТ –
предел функции в точке И предел функции на бесконечности.
Ньютон
Эйлер
Лагранж
Больцано
Коши
Слайд 4Было домашнее задание на сегодня:
+ знать ответы на следующие вопросы:
С какими
математиками связано понятие «Предел»?
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.
Слайд 5ТЕОРЕМА 1.
Предел СУММЫ (разности) 2-х функций равен СУММЕ (разности) их
пределов, если последние существуют:
Слайд 7ТЕОРЕМА 3.
Предел ПРОИЗВЕДЕНИЯ 2-х функций равен ПРОИЗВЕДЕНИЮ их пределов, если
последние существуют:
Слайд 8ТЕОРЕМА 4.
Предел ОТНОШЕНИЯ 2-х функций равен ОТНОШЕНИЮ их пределов, если
последние существуют и ПРЕДЕЛ ЗНАМЕНАТЕЛЯ ОТЛИЧЕН ОТ 0:
Слайд 14Домашнее задание
Дорешать примеры (всего должно быть 13 примеров)
Выписать таблицу производных позади
тетради
06.09.2016