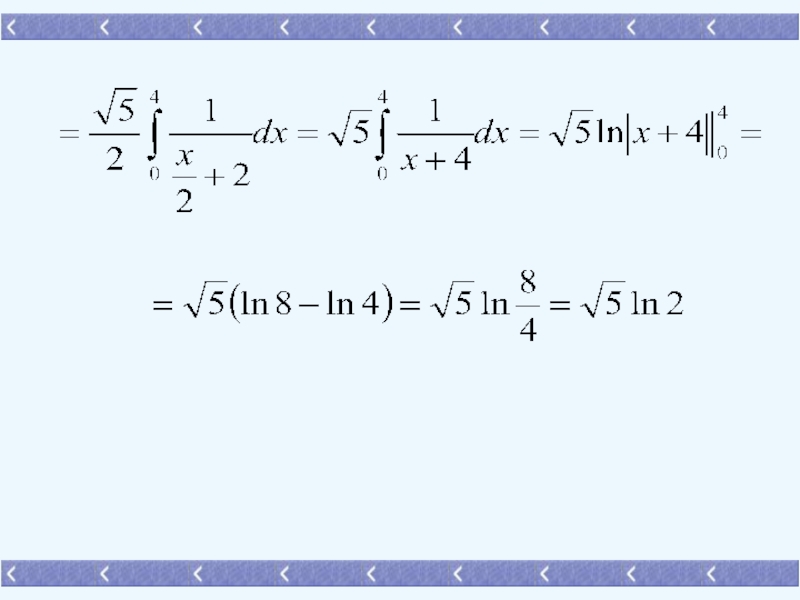L положение точки М определяется длиной дуги АМ=S, отсчитываемой от начальной точки А.
Тогда кривая L параметрически выразится уравнениями вида
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление криволинейных интегралов 1 рода презентация
Содержание
- 1. Вычисление криволинейных интегралов 1 рода
- 2. При этом функция f(x,y) сведется к сложной
- 3. Тогда интегральная сумма для криволинейного интеграла станет
- 4. 1
- 5. Пусть теперь кривая L задана параметрически: где и функции непрерывны вместе со своими производными.
- 6. Если возрастанию дуги S=AM=S(t) отвечает возрастание параметра
- 7. 2
- 8. Таким образом, для вычисления криволинейного интеграла 1
- 9. Если кривая L задана явным уравнением: где тогда и выражение (2) преобразуется к виду:
- 10. 3
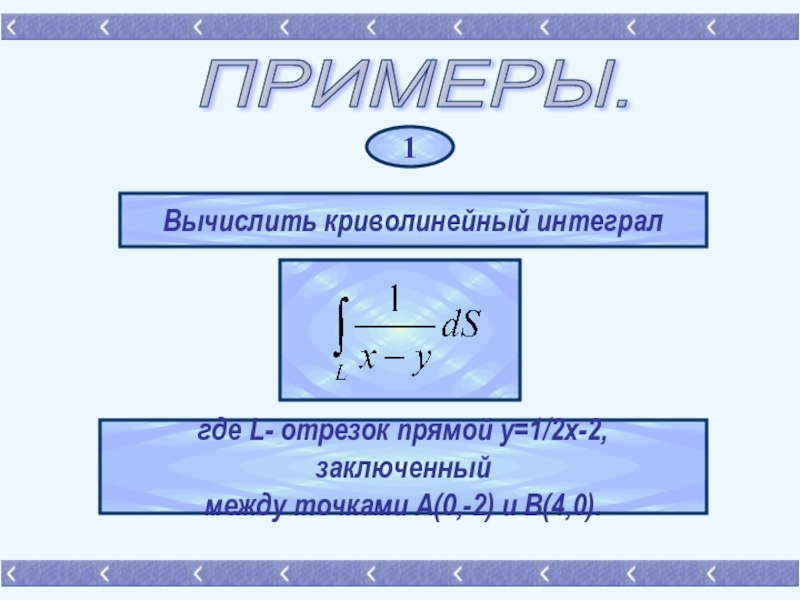
- 11. ПРИМЕРЫ. 1 Вычислить криволинейный интеграл где
- 12. РЕШЕНИЕ.
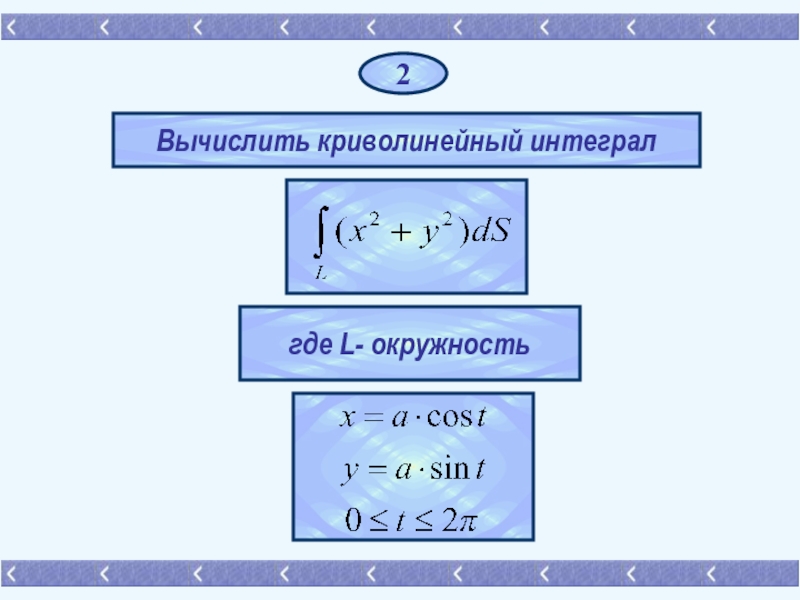
- 14. 2 Вычислить криволинейный интеграл где L- окружность
- 15. РЕШЕНИЕ.
При этом функция f(x,y) сведется к сложной функции f(x(s),y(s)). Пусть si – длины дуг, соответствующие выбранному делению дуги АВ точками Ai. Тогда Пусть - значение s, определенное точкой Мi.
Слайд 2При этом функция f(x,y) сведется к сложной функции f(x(s),y(s)).
Пусть si –
длины дуг, соответствующие выбранному делению дуги АВ точками Ai. Тогда
Пусть
- значение s, определенное точкой Мi.
Слайд 3Тогда интегральная сумма для криволинейного интеграла станет интегральной суммой определенного интеграла:
Тогда
криволинейный интеграл 1 рода сводится к определенному интегралу по формуле:
Слайд 5Пусть теперь кривая L задана параметрически:
где
и функции
непрерывны вместе со своими производными.
Слайд 6Если возрастанию дуги S=AM=S(t) отвечает возрастание параметра t, то
Заменяя в (1)
переменную в интеграле, получаем:
Слайд 8Таким образом, для вычисления криволинейного
интеграла 1 рода надо заменить в
подынтегральном
выражении переменные х и у
через параметр, а дифференциал дуги dS
выразить как функцию параметра.
через параметр, а дифференциал дуги dS
выразить как функцию параметра.
Слайд 11ПРИМЕРЫ.
1
Вычислить криволинейный интеграл
где L- отрезок прямой y=1/2x-2, заключенный
между точками А(0,-2) и
В(4,0).
