- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выборочный метод в статистике презентация
Содержание
- 1. Выборочный метод в статистике
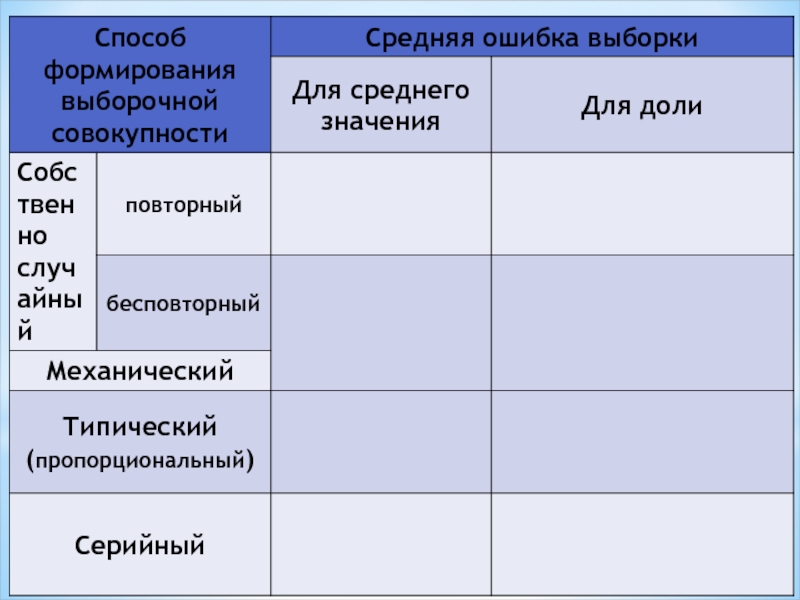
- 2. Вопросы: Средняя ошибка выборки для
- 3. В выборочной совокупности дисперсия для доли
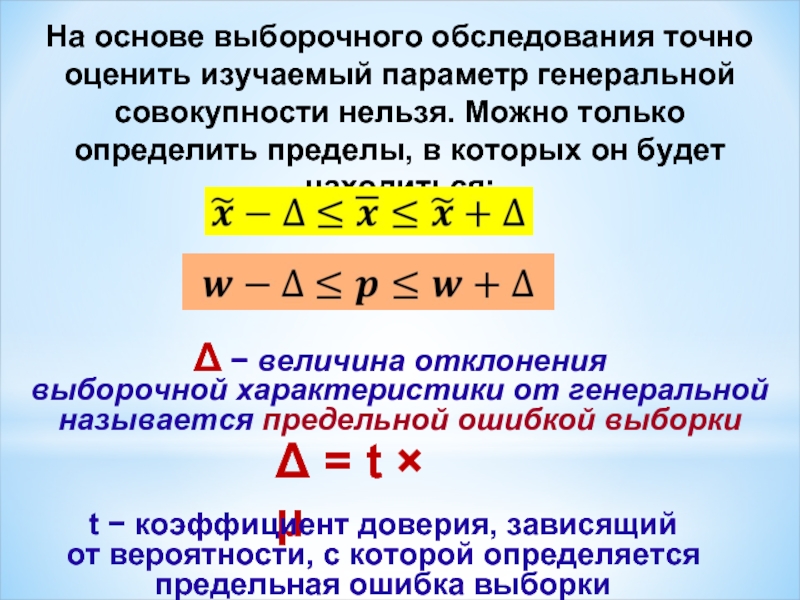
- 5. На основе выборочного обследования точно оценить изучаемый
- 6.
- 7.
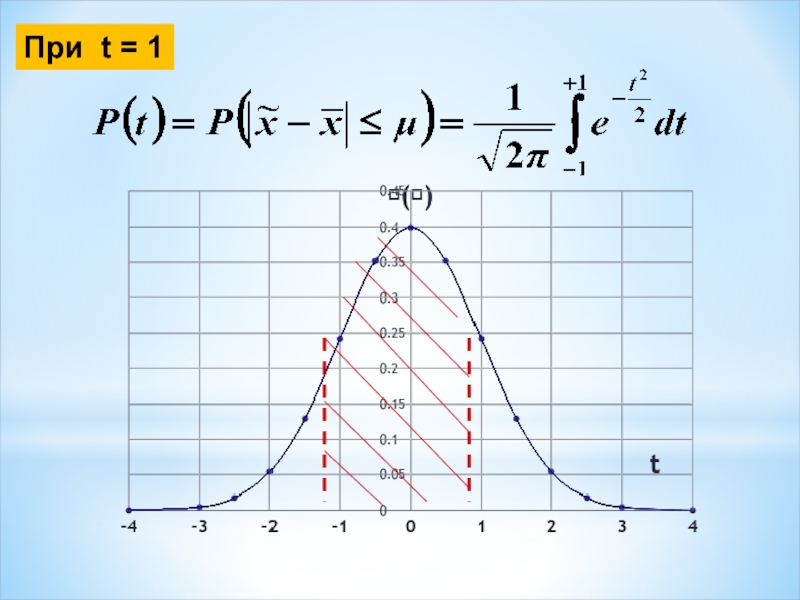
- 8. При t = 1
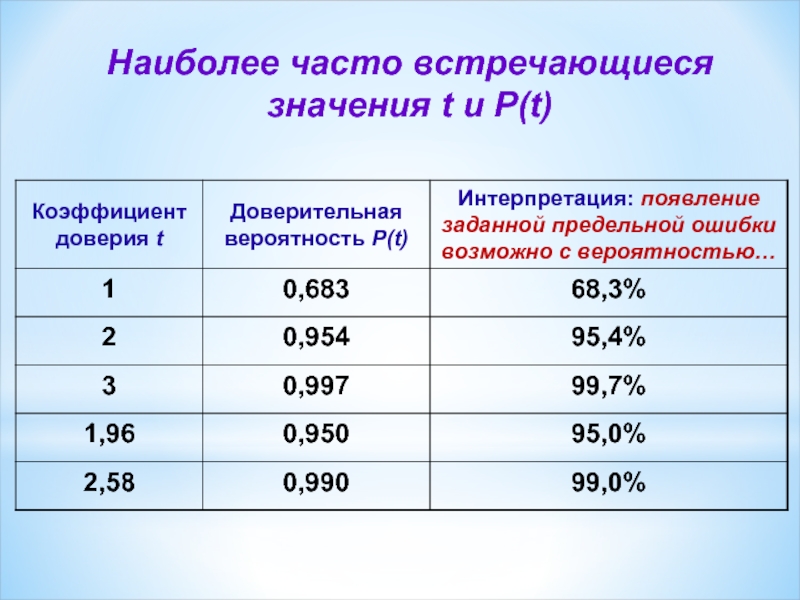
- 9. Наиболее часто встречающиеся значения t и P(t)
- 10. Значения интеграла Лапласа для разных значений t
- 11. Наряду с абсолютной величиной средней и
- 12. Распространение результатов выборочного наблюдения на
- 13. Если результаты выборочного наблюдения можно распространять
- 14. Критерий репрезентативности выборочной совокупности
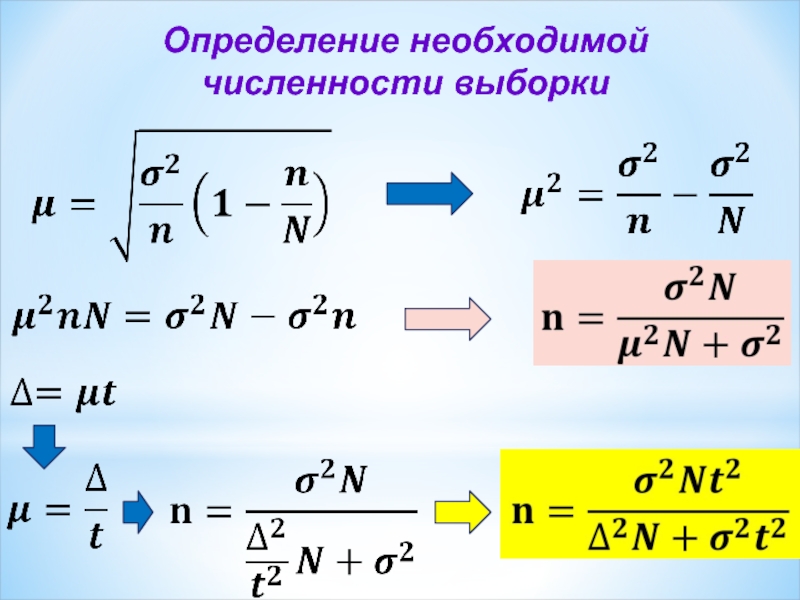
- 15. Определение необходимой численности выборки
- 16. Возможные подходы: исходя из результатов предыдущих обследований
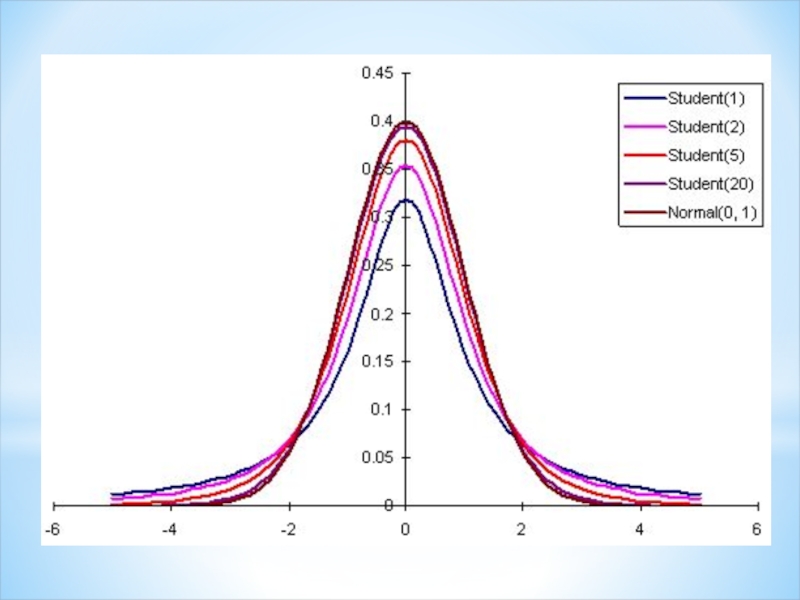
- 17. Малая выборка
- 18. Выборка считается малой, если обследуется не
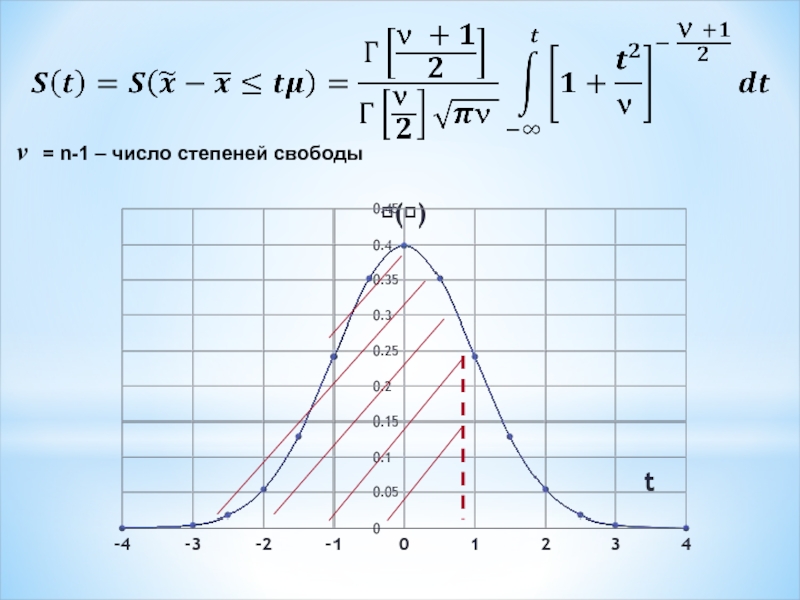
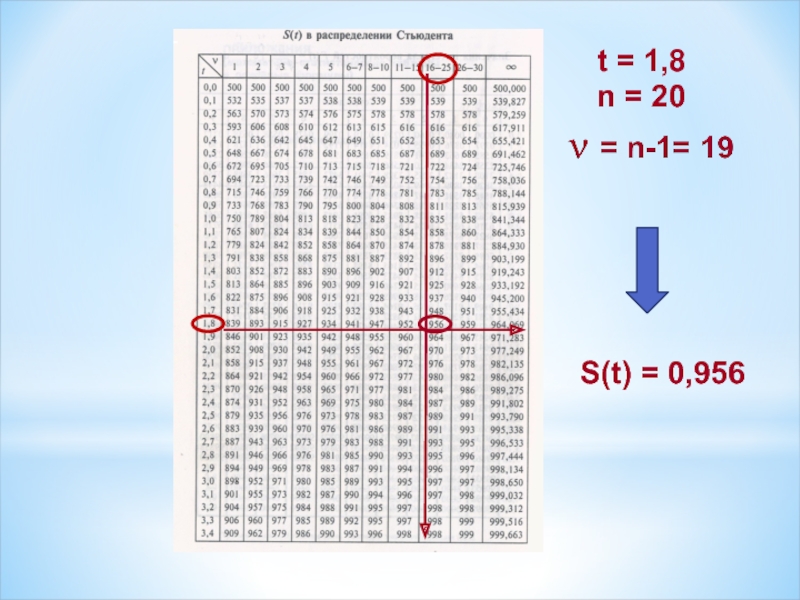
- 20. ν = n-1 – число степеней свободы
- 21. n = 20 t = 1,8 S(t) = 0,956
- 22. S(t) – вероятность того, что
- 23. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Вопросы:
Средняя ошибка выборки для доли.
Виды ошибок выборки, распространение результатов выборочного
Определение необходимой численности выборки.
Малая выборка.
Слайд 3В выборочной совокупности дисперсия
для доли рассчитывается по формуле:
Межсерийная дисперсия для
где
Слайд 5На основе выборочного обследования точно оценить изучаемый параметр генеральной совокупности нельзя.
Δ − величина отклонения
выборочной характеристики от генеральной
называется предельной ошибкой выборки
Δ = t × μ
t − коэффициент доверия, зависящий
от вероятности, с которой определяется предельная ошибка выборки
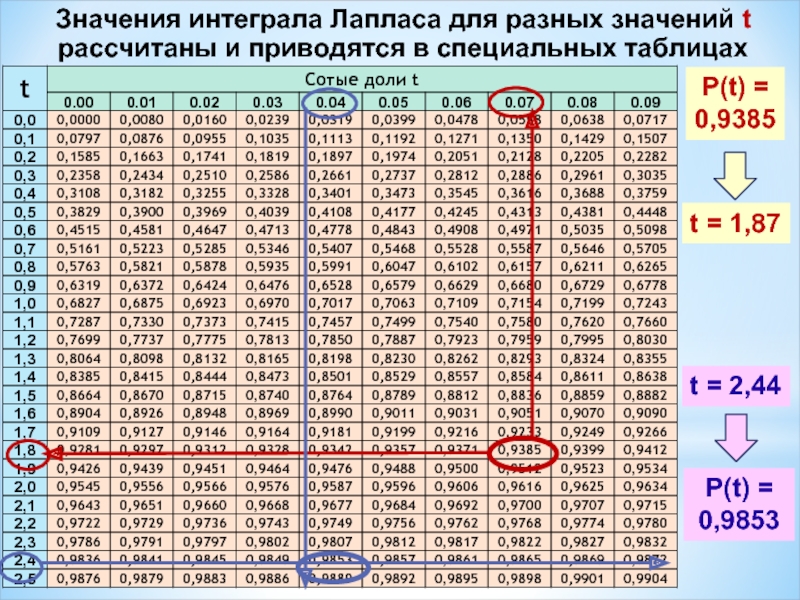
Слайд 10Значения интеграла Лапласа для разных значений t рассчитаны и приводятся в
P(t) =
0,9385
t = 1,87
t = 2,44
P(t) =
0,9853
Слайд 11Наряду с абсолютной величиной средней и предельной ошибки выборки в статистической
Теоретически в знаменателе должно стоять значение исследуемого параметра генеральной совокупности.
Однако, учитывая, что оно неизвестно, относительная ошибка рассчитывается через соответствующий параметр выборки.
или
Слайд 12Распространение результатов
выборочного наблюдения
на генеральную совокупность
При распространении результатов выборочного наблюдения
указывать вероятность, с которой гарантируется этот результат
!
Слайд 13Если результаты выборочного наблюдения можно распространять
на генеральную совокупность, то такая
Всегда ли результаты выборочного наблюдения можно распространять
на генеральную совокупность
Слайд 16Возможные подходы:
исходя из результатов предыдущих обследований (выборочных или сплошных), либо специально
исходя из гипотезы о законе распределения изучаемого признака в генеральной совокупности. Если распределение близко к нормальному, то размах вариации (R) в 6 раз больше среднего квадратического отклонения
если в результате обследования необходимо установить долю единиц, обладающих определенным значением альтернативного признака. Дисперсия альтернативного признака равна σ2=pq, где p – доля единиц, обладающих изучаемым признаком; q – доля единиц, не обладающих им. Максимальное значение дисперсии альтернативного признака равно 0,25 при p = q = 0,5
Оценка дисперсии изучаемого признака при определении необходимой численности выборки
Слайд 18Выборка считается малой, если
обследуется не более 30 единиц
Средняя ошибка малой
В случае малой выборки в условиях нормально распределенной генеральной совокупности вероятность появления нормированного отклонения выборочной средней от генеральной
подчиняется закону распределения Стьюдента
Слайд 22
S(t) – вероятность того, что фактическое
значение нормированного отклонения
выборочной средней от
не превышает значения предельной ошибки
P(t) – вероятность того, что фактическое
значение нормированного отклонения выборочной средней от генеральной
по абсолютной величине не превышает значения предельной ошибки